• 컴퓨터 과학은 문제 해결에 대한 학문이고 문제 해결이란 어떠한 입력 값을 전달받아 원하는 출력 값을 만드는 과정이라고도 볼 수 있습니다. 이러한 입력과 출력을 컴퓨터에서 전달받고 저장하고 해결하기 위해 사용하는 데이터 표현법이 2진법입니다.
• 그러면 우선 2진법부터 알아보겠습니다.

컴퓨터의 표현법 : 2진법

• 2진법은 숫자 0과 1로만 데이터를 표현하는 것입니다. 저희가 흔히 사용하는 10진법은 0, 1, 2, 3, 4, 5, 6, 7, 8, 9로 데이터를 표현합니다.
• 우선 2진법과 10진법은 표현하는 숫자만 다르지 원리는 같습니다.

10진법

• 10진법은 각 자리는 10의 제곱수이며 일의 자리수를 채우면 십의 자리수가 채워지고 백의 자리수가 채워집니다. 만약 123456이라는 숫자가 있으면 각 자릿수는 다음과 같습니다.

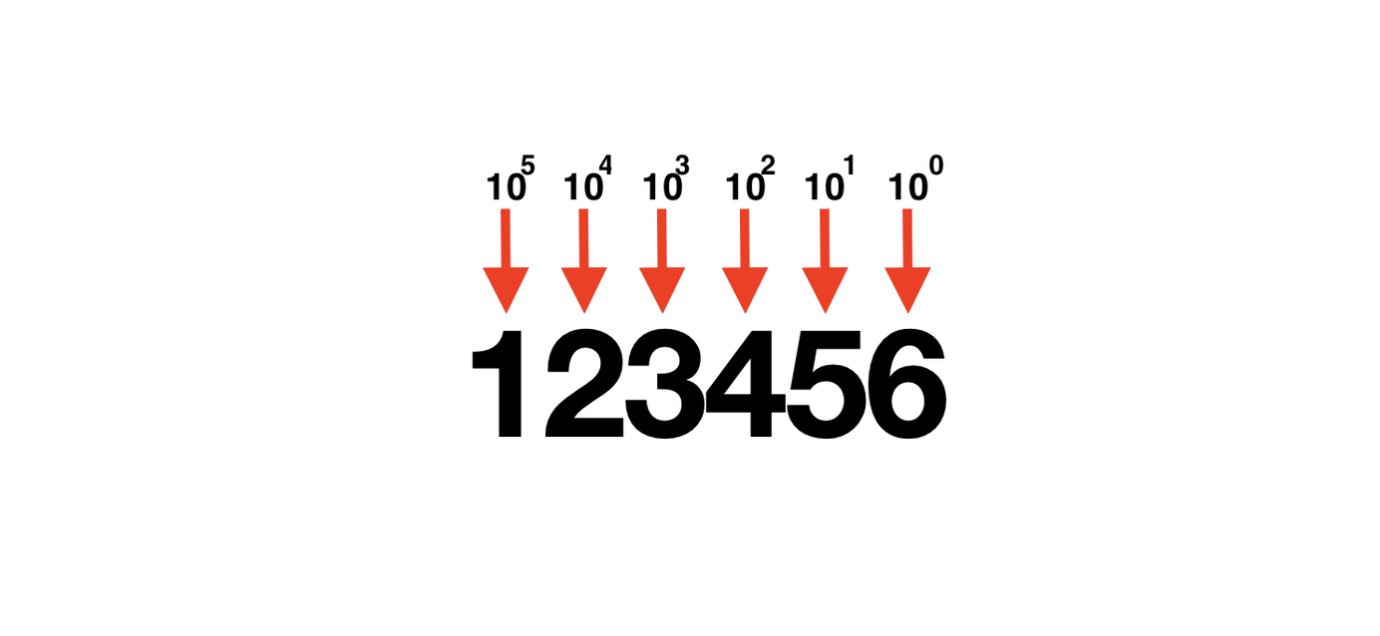
• 계산은 다음과 같습니다.

(1*10^5) + (2*10^4) + (3*10^3) + (4*10^2) + (5*10^1) + (6*10^0)

• 예를 들어 아래와 같이 사용됩니다.

1, 2, ... 8, 9, 10, 11, ... 98, 99, 100, 101, ... 998, 999, 1000, 1001

• 한 자리에 수가 끝(9)까지 차면 자릿수가 올라가여 올라간 자릿수는 1부터 다시 시작하고 원래 자릿수는 0이 되는 것이죠
• 10진법에서 9에서 1이 더해져 10이 되는 과정은 아래와 같습니다.

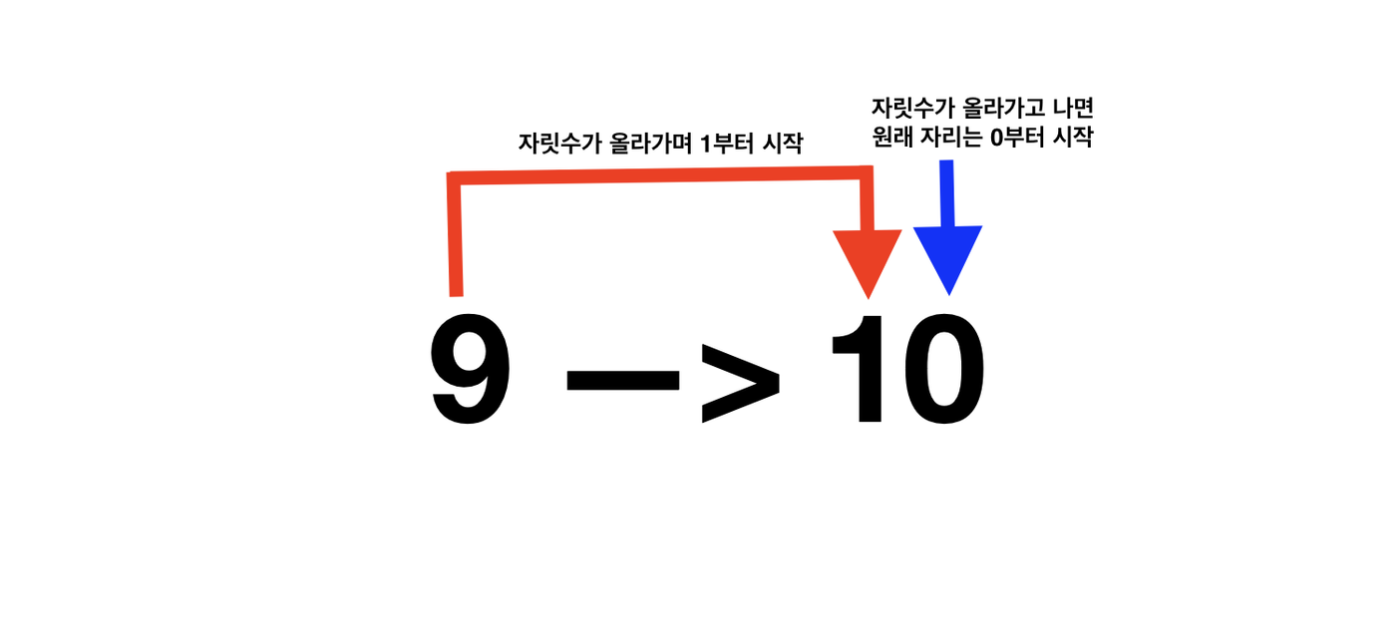
• 이렇듯 각 자릿수가 10의 제곱수로 표현되니 10진수라 불립니다.

2진법

• 2진법도 같습니다. 0과 1로 데이터를 표현하고 각 자릿수는 2의 제곱수로 나타납니다. 만약 5라는 숫자를 이진수로 표현한다면 다음과 같습니다.

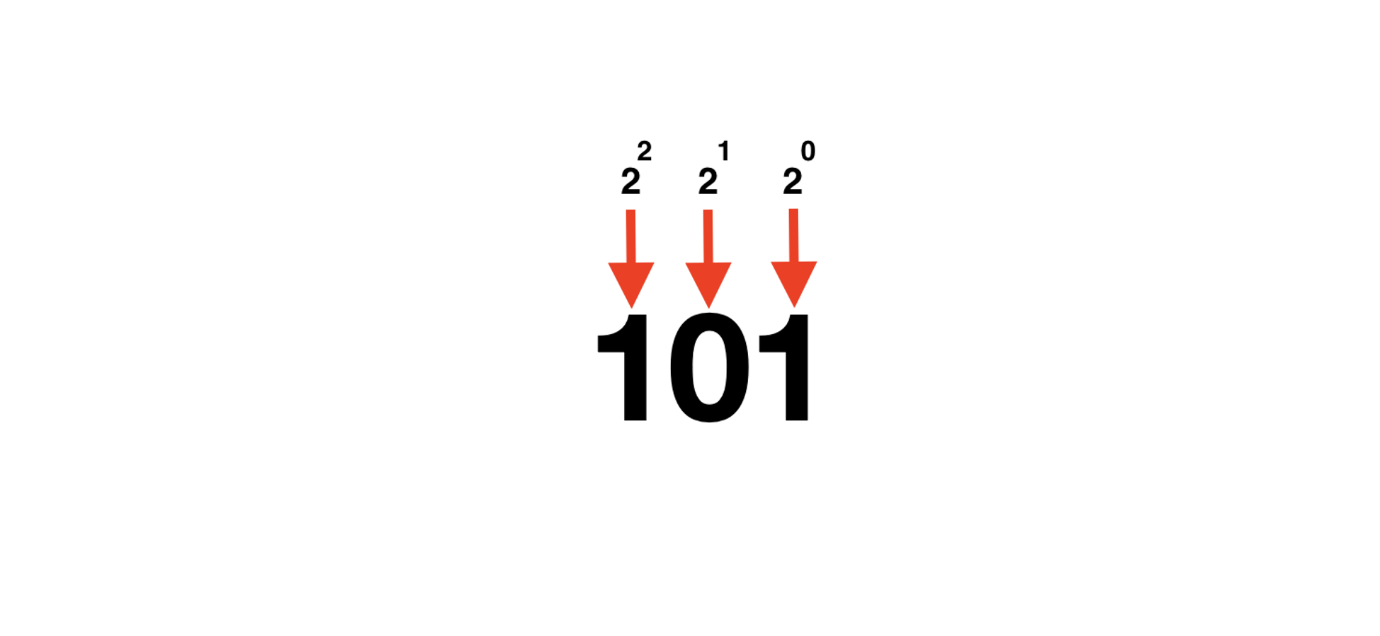
• 계산은 다음과 같습니다.

(1*2^2) + (0*2^1) + (1*2^0)

• 2진법 또한 10진법처럼 한 자리에 수가 끝(1)까지 차면 자릿수가 올라가여 올라간 자릿수는 1부터 다시 시작하고 원래 자릿수는 0이 됩니다.
• 2진법에서 1에서 1이 더해져 2가 되는 과정은 아래와 같습니다.

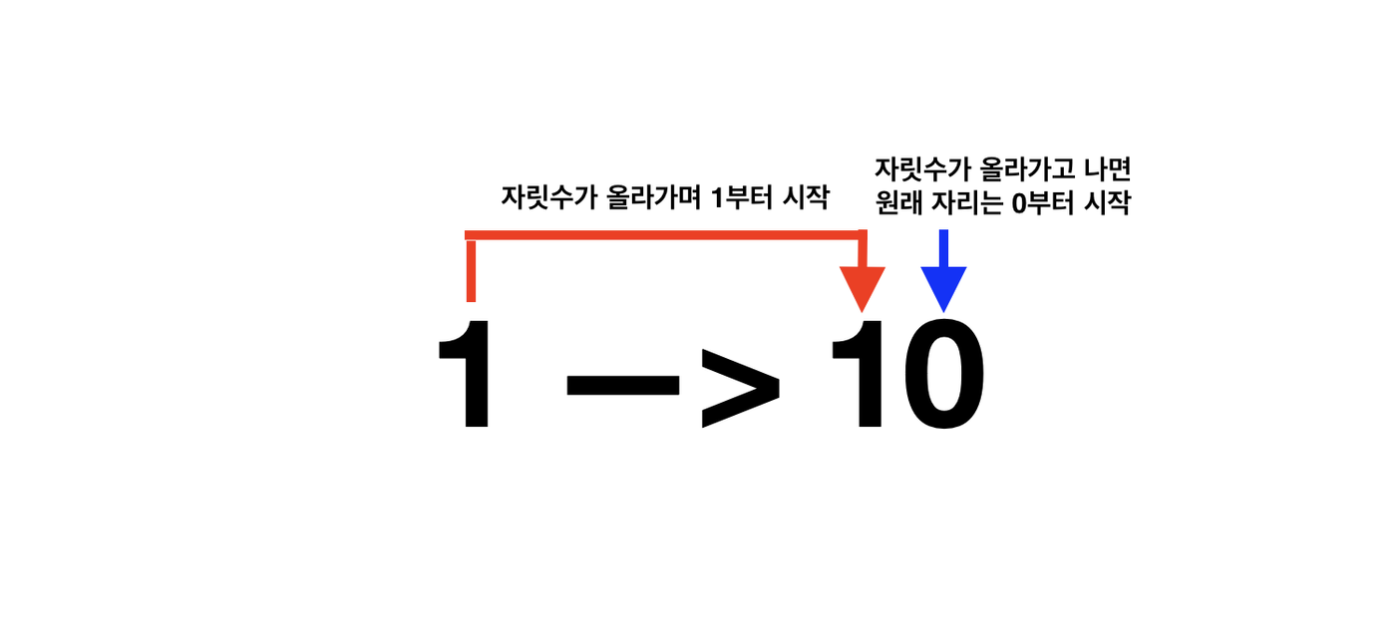
• 이러한 2진법로 컴퓨터 정보를 표현하고 이러한 2진수를 비트라고 합니다.

비트(bit)

• 비트는 단지 2진수를 뜻하고 0과 1을 뜻합니다.
• 컴퓨터는 이러한 많은 수의 비트를 사용하여 정보를 표현합니다.
• 벽에 플러그를 꽂거나 전구를 켜거나 스위치 등을 활용하는 것도 0과 1로 표현할 수 있습니다.
• 컴퓨터 안의 작은 스위치인 트랜지스터로 이러한 비트를 저장합니다. 트랜지스터를 물리적으로 이용해서 정보를 표현하고 값을 저장합니다.
• 이러한 비트를 많이 사용하기 위해 8bit 단위로 묶어놓은 것이 byte입니다.
• 바이트는 8개의 1과 0을 나타내는 단위입니다.

0.1 + 0.2 = 0.3가 아닌 이유

• 이제 컴퓨터에서의 데이터 표현법을 알았으니 0.1 + 0.2 ≠ 0.3인 이유를 알아보겠습니다.
• 위에서 말했듯이 컴퓨터는 숫자를 이진수로 저장하고 표현합니다. 그렇다면 소수는 어떻게 표현할까요?
• 위 방법과 같습니다. 소수점을 두고 2의 마이너스 제곱으로 칸을 표기합니다. 예를 들어 0.125를 저장하는 방법은 다음과 같습니다.

(2^-1) * 0 + (2^-2) * 0 + (2^-3) * 1 = 0.125 
=> 0.001

• 그렇다면 5.125는 어떻게 표현할까요? 소수점을 기준으로 따로 변환하여 다음과 같이 표현하면 됩니다.

101.001

• 하지만 나중에 연산을 편리하게 하기 위해 IEEE(Institute of Electrical and Electronics Engineers)에서 권장하는 거의 모든 컴퓨터에서 사용하는 저장 방법이 있습니다.
• 우선 5.125의 변환 방법부터 알아보겠습니다.

  1. 첫 번째로 저장공간을 32칸정도로 넉넉하게 잡고 첫 칸에 양수/음수 여부부터 넣습니다. 여기서 양수는 0, 음수는 1로 나타냅니다.

     **0ㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ
     ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ**

  2. 위에서 계산하였던 101.001을 한자릿수로 나타내줍니다. ⇒ 1.01001 * 2^2 (소수점 아래 01001을 mantissa 부분이라 부릅니다.)

  3. mantissa부분을 뒤 23칸에 넣어줍니다.

     **0ㅁㅁㅁ ㅁㅁㅁㅁ ㅁ010 0100 0000 0000 0000 0000
     0000 0000 0000 0000 0000 0000 0000 0000**

  4. 지수인 2에 127을 더하고 이진수로 변환하여 남은 자리에 넣어줍니다. 129 ⇒ 1000 0001

     **0100 0000 1010 0100 0000 0000 0000 0000
     0000 0000 0000 0000 0000 0000 0000 0000**

• c언어 같은 곳에서 소수를 저장하는 float같은 곳에 저장할 때 이러한 방식으로 저장합니다. 하지만 이러한 부분에는 문제가 존재합니다.

순환 소수 문제

• 위에서 예로 보았던 0.125와 같은 수는 이진수 0.001로 딱 맞아 떨어집니다. 하지만 0.1과 같은 수는 이진수로 변환하면 다음과 같이 패턴을 가지고 무한히 반복됩니다.

0.0001 1001 1001 1001 1001 1001 1001 1001
1001 1001 1001 1001 1001 1001 1001 1001 ...

• 하지만 컴퓨터는 이런 무한한 이진수를 저장할 공간이 없기 때문에 위에서 말했던 방법으로 32비트를 초과하는 자리를 다 잘라버립니다. 위와 같은 방법으로 변환해보면 아래와 같이 됩니다.

  1. 첫 번째로 저장공간을 32칸정도로 넉넉하게 잡고 첫 칸에 양수/음수 여부부터 넣습니다. 여기서 양수는 0, 음수는 1로 나타냅니다.

     **0ㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ
     ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ ㅁㅁㅁㅁ**

  2. 위에서 계산하였던 0.00011001…을 한자릿수로 나타내줍니다. ⇒ 1.10011001… * 2^(-4)

  3. mantissa부분을 뒤 23칸에 넣어줍니다.

     **0ㅁㅁㅁ ㅁㅁㅁㅁ ㅁ100 1100 1100 1100 1100 1100
     1100 1100 1100 1100 1100 1100 1100 1100...**

  4. 지수인 -4에 127을 더하고 이진수로 변환하여 남은 자리에 넣어줍니다. 123 ⇒ 0111 1011

     **0011 1101 1100 1100 1100 1100 1100 1100
     1100 1100 1100 1100 1100 1100 1100 1100...**

• 이렇게 변환되면 그 뒤 무한히 반복되는 1100 1100 1100…이 잘리게 되고 이 부분이 오차로 존재하게 됩니다.
• 이렇게 하여 잘린 부분이 오차가 되고 0.1을 이진수로 변환하면 정확하게 0.1에 대한 이진수가 저장되는 것이 아닌 위에서 잘린 1100 1100..을 오차로 가진 0.1이 저장되어 컴퓨터에서 0.1 + 0.2 ≠ 0.3이 되는 것입니다.

결론

• 컴퓨터는 숫자 신호를 판단하는데 많은 자원을 사용하기 때문에 이진수를 사용하여 데이터를 저장하고 표현합니다.
• 나중에 시간이 흘러 10가지 서로 다른 상태를 나타낼 수 있고도 가볍고 전력소모가 작은 소자가 나타나면 십진수 컴퓨터가 생길 수도 있을 것 같습니다!
• 마지막으로 제가 알고리즘 문제를 풀 때 주로 사용하는 파이썬으로 0.1 + 0.2 ≠ 0.3이라는 결과가 나오는 것을 확인하고 포스팅을 마치도록 하겠습니다!