알고리즘

에라토스테네스의 체는 소수를 찾는 방법2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)자기 자신을 제외한 2의 배수를 모두 지운다.남아있는 수 가운데 3은 소

유클리드 호제법 또는 유클리드 알고리즘은 2개의 자연수 또는 정식의 최대공약수를 구하는 알고리즘의 하나이다.1071과 1029의 최대공약수를 구하면,1071은 1029로 나누어 떨어지지 않기 때문에, 1071을 1029로 나눈 나머지를 구한다. ≫ 421029는 42로

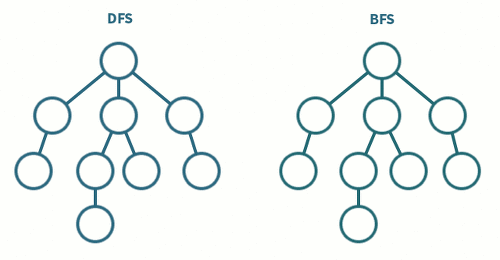
그래프를 탐색하는 방법에는 크게 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)이 있습니다.루트 노드( 혹은 다른 임의의 노드)에서 다음 분기(branch)로 넘어가기 전에, 해당 분기(branch)를 모두 탐색하는 방법. 탐색 후에는 다시 원점으로 돌아가 다른 분

그리디 알고리즘은 "현재 상황에서 지금 당장 좋은 것만 고르는 방법"을 선택해 전체 적합한 결과를 도출하자는 알고리즘 기법입니다. 순간 가장 좋아보이는 것을 선택하며, 현재의 선택이 나중에 미칠 영향에 대해서는 고려하지 않습니다.위의 예시와 같이 최초의 선택에서 최적

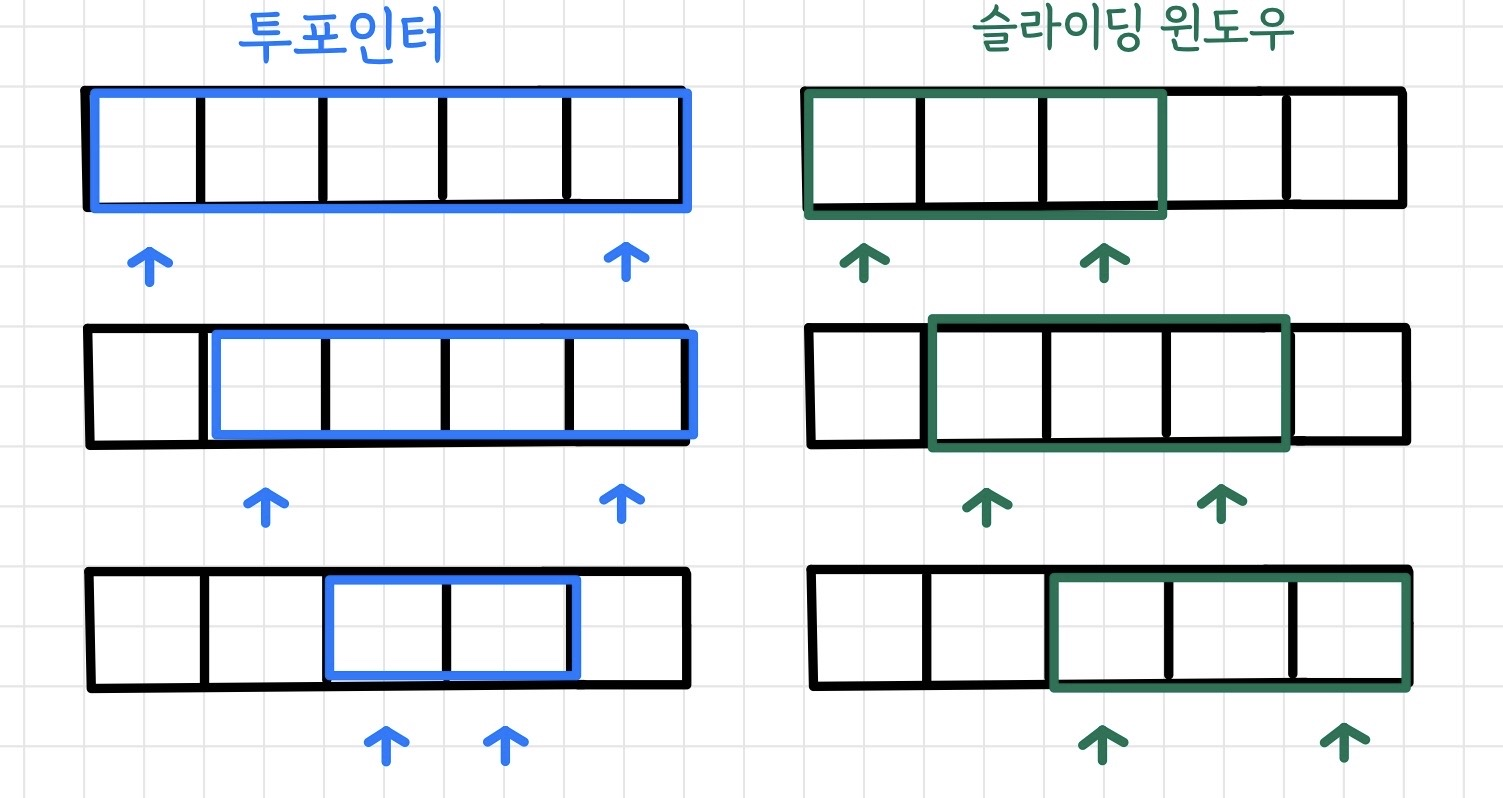
슬라이딩 윈도우 기법은 배열에서 연속된 부분 배열의 최대 합을 효율적으로 구하는 방법 중 하나입니다. 이 기법은 고정된 크기의 윈도우를 배열에서 이동하면서 부분 배열의 합을 계산하고, 최대 합을 찾는 방식으로 동작합니다. 주어진 문제가 부분 배열의 합을 구하는 것이라

이분 탐색 / 이진 탐색 (Binary Search) 정렬된 배열 또는 리스트에 적합한 고속 탐색 방법이다. 배열의 중앙에 있는 값을 조사하여 찾고자 하는 항목이 왼쪽 또는 오른쪽 부분 배열에 있는지를 알아내어 탐색의 범위를 반으로 줄인다. 찾고자 하는 값이 속해있지

피보나치 함수는 f(n) = f(n-1) + f(n-2)로 나타낼 수 있다.f(n-1) = f(n-2) + f(n-3)f(n-2) = f(n-3) + f(n-4)볼드로 표시한 함수는 중복으로 계산된다. 게다가 저 항들을 계산하기 위해 수많은 하위 노드들을 또 계산해야

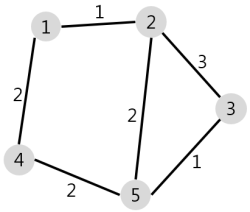
다익스트라 알고리즘은 DP활용한 최단경로 탐색 알고리즘입니다. 특정한 하나의 노드에서 특정한 노드로 가는 최단경로를 알려줍니다. 이 때 음의 간선을 포함할 수 없습니다. gps와 같이 실제로 사용하기 적합한 알고리즘입니다. 다익스트라 알고리즘이 DP인 이유최단 거리는

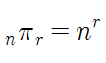
순열이란 서로 다른 n개중에 r개를 선택하는 경우의 수를 의미합니다. (순서 상관 있음)첫번째는 swap 함수를 만들어서 배열들의 값을 직접 바꾸는 방법입니다.배열의 첫 값부터 순서대로 하나씩 바꾸며 모든 값을 한번씩 swap 합니다.depth 를 기준 인덱스로 하여

수열 An에 대해서, 구간 \[1, 1]의 합, 구간 \[1, 2]의 합, 구간 \[1, 3]의 합, ..., \[1, n]의 합을 누적 합이라고 한다.하지만 이렇게 모든 입력마다 구간합을 일일히 구해주는 경우에는 구간의 길이가 M이라고 하면 매 구간합을 구할 때 마다

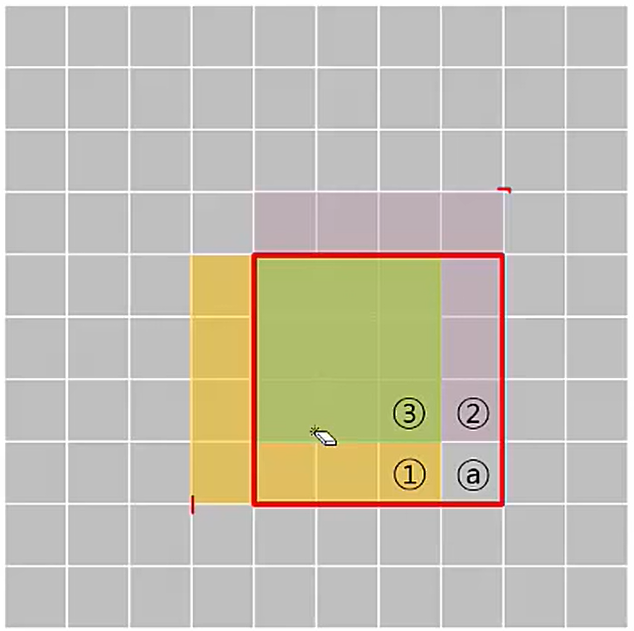
기본적인 아이디어로 하나의 큰 문제를 여러 개의 작은 문제로 나누어서 그 결과를 저장하여 다시 큰 문제를 해결할 때 사용하는 것으로 특정한 알고리즘이 아닌 하나의 문제해결 패러다임으로 볼 수 있다. 간단히 말해서 답을 재활용하는 것이다.이럴 때 DP를 사용하면 된다.

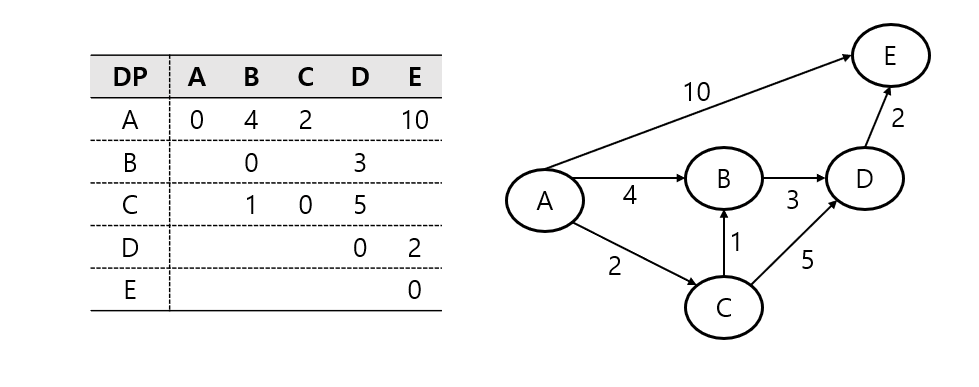
모든 노드간에 최단거리를 구하는 알고리즘다익스트라, 벨만포드는 한 노드에서 모든노드까지의 최단경로Floyd-Warshall은 모든노드에서 모든노드까지의 최단 경로벨만포드와 같이 가중치에 음수가 있어도 가능음수 순환 사이클이 없는 그래프에서, 모든 점에서 모든 점까지의

카탈란 수는 조합론에서 중요한 역할을 하는 수열로, 많은 수학적 문제와 프로그래밍 문제에서 나타납니다. 이 수열은 다양한 조합 문제에서 발생하는 경우의 수를 계산하는 데 사용됩니다.카탈란 수 $$( C_n )$$은 다음과 같은 방법으로 정의됩니다:$$C_n = \\fr

파스칼의 삼각형은 이항 계수의 수학적 배열을 삼각형 형태로 나타낸 것입니다. 프랑스의 수학자 블레즈 파스칼의 이름을 따서 명명된 이 도구는 간단하면서도 강력하여, 이항 계수를 시각적으로 나타내는 데 중요한 역할을 합니다. 이는 조합론에서만 중요한 것이 아니라, 이항 전

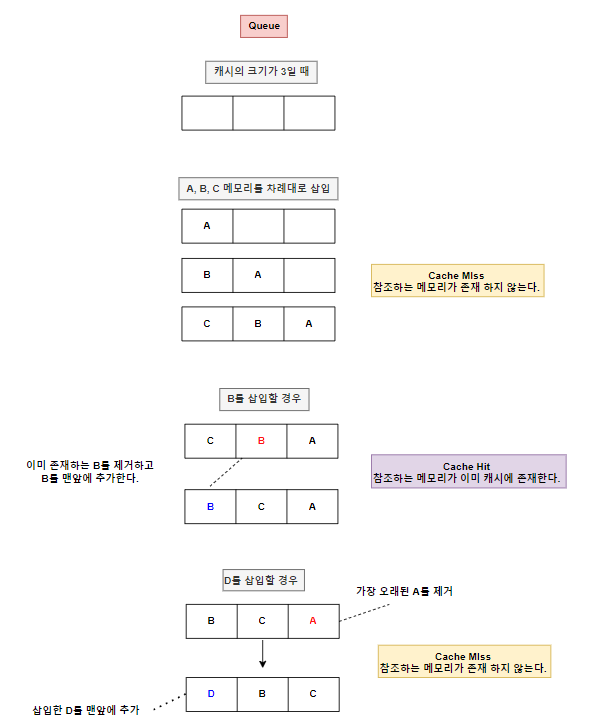
LRU(Least Recently Used) 알고리즘은 캐시 메모리 관리에서 가장 많이 사용되는 방법 중 하나입니다. 이 알고리즘의 기본 원리는 가장 오랫동안 사용되지 않은 데이터를 교체하는 것입니다. 즉, 캐시가 가득 찼을 때 가장 최근에 사용된 적이 없는 데이터를

안정 정렬은 데이터의 순서를 유지하면서 정렬하는 알고리즘을 의미합니다. 예를 들어, 중복된 값이 있을 때, 원래의 입력 순서가 유지되는 것이죠. 이러한 특성 덕분에 안정 정렬은 데이터의 일관성을 보장하는 데 유용합니다.안정 정렬(Stable Sort)은 동일한 키 값을

Kruskal 알고리즘은 연결된 가중 그래프의 최소 신장 트리(MST)를 찾기 위한 인기 있는 알고리즘입니다. 이 알고리즘은 모든 간선을 가중치의 비내림차순으로 정렬한 후, 하나씩 추가하면서 사이클을 형성하지 않는 경우에만 포함시킵니다.모든 간선 정렬: 그래프의 모든