가중치 초기화는 신경망 제작에 있어 중요하다.
첫 가중치를 무슨 값으로 하느냐에 따라 결과가 천차만별이 되기 때문이다.
가중치 설정의 중요성과 Xavier Initialization 식을 유도해보자.
가중치가 너무 작다면?
만약 가중치가 너무 작다면 발생하는 문제를 살펴보자.
예시로 사용한 구조는 500개의 neuron을 가진 10 layer 신경망이다. 활성화 함수는 tanh를 사용했다. 이를 0.01 * np.random.randh(D,H)로 초기화했다고 가정하자.
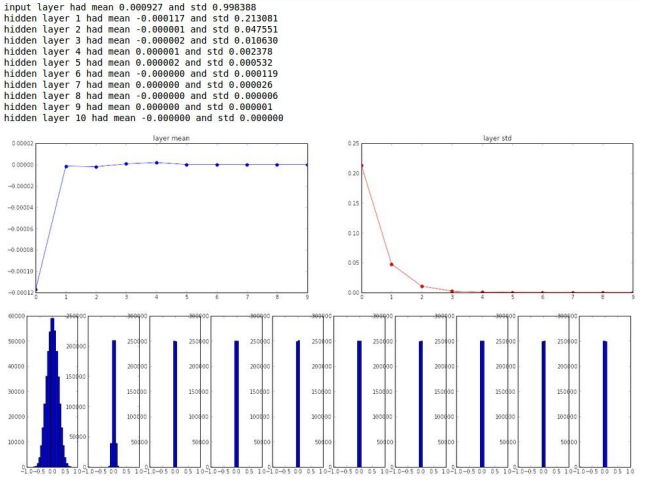
각 레이어 별 activation 정도이다.
Layer를 지나면 지날수록 mean, std가 0으로 수렴하는 것을 보인다. 이유가 무엇일까?
활성화 함수를 f라 하였을 때, 다음 layer로 넘어가는 activation은 다음과 같다.
여기서 w가 너무 작은 값이기에 다음 layer의 input도 아주 작은 값이 되고, 점점 지나며 0으로 수렴한다. tanh 함수는 zero-center 활성화 함수이기에 f를 통과해도 0으로 수렴하는 결과를 얻는다.
그렇다면 역전파의 경우는 어떨까?
이 경우에서는 식을 살펴보자.
활성화 함수를 f, 활성화 함수 input 값을 z라 하면 다음과 같은 식을 얻는다. 여기서 이므로
가 된다. 가 아주 작은 값이기에 도 아주 작은 값이 되어 가중치 update가 일어나지 않는다.
가중치가 너무 크다면?
가중치가 너무 큰 경우를 살펴보자. 이번에는 1.0 * np.random.randh(D,H)으로 초기화 했다고 가정하자.
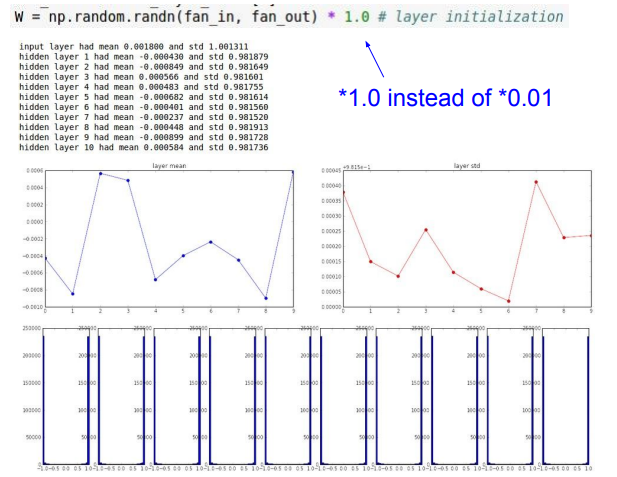
Jesus! 값이 이번에는 모두 양극단으로 치우친다. 이 원인은 tanh 함수의 모양 때문이다.
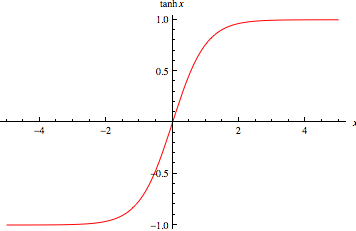
여기서 보면 알 수 있듯이 tanh는 값이 크면 1에 수렴하고, 작으면 -1에 수렴한다. 앞서 에서 값이 크기 때문에 값이 매우 커지거나 작아진다. 즉 양 극단으로 튀는 것이다. 이 상태를 Saturated된 상태라고 하는데, 말 그대로 포화된 상태라 -1, 1 값만 나오는 것이다.
tanh 함수 특성상 양 끝으로 가면 기울기가 0으로 수렴하기에 가중치 update 역시 되지 않는다.
Xavier Initialization
그렇다면 올바른 가중치 조건은 무엇일까? Input과 Output의 분산이 같다면 될 것이다.
왜냐하면 끊임없이 layer를 쌓더라도 분산이 변하지 않으면 activation이 어디에 몰리는 현상 없이 계속 유지될 것이기 때문이다.
이 아이디어를 기반으로 Xavier Initialization을 유도해보자.
Xavier Initialization은 몇 가지 가정이 필요하다.
1) 활성화 함수가 선형이다 -> tanh는 0 근처에서 선형이다. 우리는 input이 0 근처라고 가정한다.
2) Input 데이터, 가중치는 서로 독립이고 평균이 0인 분포를 따른다.
이제 유도해보자.
먼저 에서 활성화 함수를 선형으로 가정했으므로 에 대해서만 살펴보자.
여기서 와 가 같아져야 하므로
이 나온다.
즉 가중치의 분산이 을 가져야 하므로 처음 Data에 으로 나눠주는 것이다.
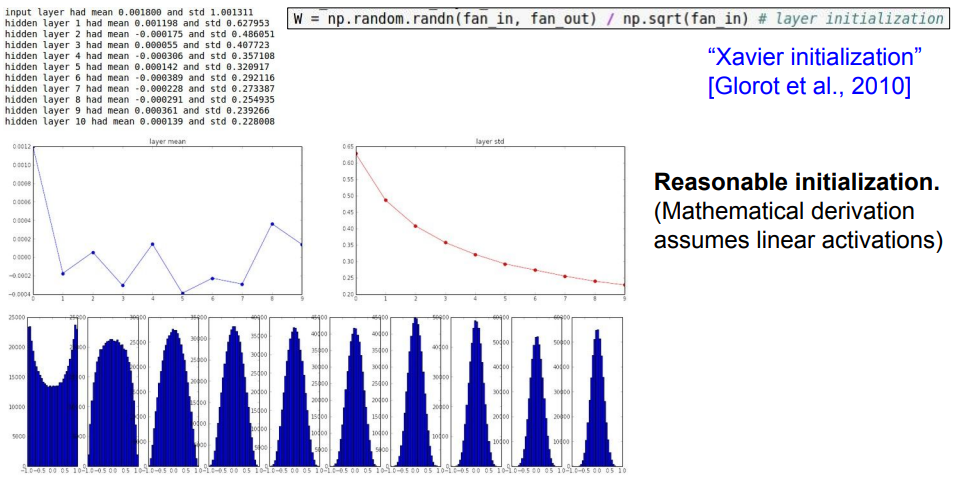
실제로도 아주 이쁘게 사용할 수 있다.
물론 여기서 가정대로 input 데이터와 가중치가 독립이 아니거나, 활성화 함수가 선형이 아니거나... 등등 여러 현실 문제로 인해 잘 맞지 않을 수 있다.
하지만 널리 쓰이는 초기값이기도 하고 웬만하면 잘 돌아가기 때문에 첫 시도로 나쁘지 않다.
Reference
https://velog.io/@iissaacc/Weight-initialization
http://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture6.pdf
https://ko.wikipedia.org/wiki/%EB%B6%84%EC%82%B0
https://calcifer1009-dev.tistory.com/11
https://velog.io/@cha-suyeon/DL-%EA%B0%80%EC%A4%91%EC%B9%98-%EC%B4%88%EA%B8%B0%ED%99%94Weights-Initialization