
머신러닝을 처음 접할 때 가장 많이 사용되는 데이터셋 중 하나가 바로 Iris 데이터셋이다.
Iris는 프랑스의 국화로, Setosa, Versicolor, Virginica 세 가지 종으로 나뉜다.
꽃받침(sepal)과 꽃잎(petal)의 길이와 너비를 측정한 데이터를 이용해 품종을 분류할 수 있다.
이번 글에서는 Iris 데이터를 이용해 의사결정나무(Decision Tree) 를 학습해보고, 엔트로피와 지니지수 같은 분류 기준도 함께 살펴본다.
데이터 불러오기와 데이터프레임 만들기
# iris 데이터 불러오기
from sklearn.datasets import load_iris
iris = load_iris()# 컬럼 (키) 확인
iris.keys()# iris의 sepal, petal 데이터프레임 만들기
import pandas as pd
iris_df = pd.DataFrame(iris.data, columns = iris.feature_names)
iris_df.head()
# species 데이터 추가
iris_df['species'] = iris.target
iris_df.head()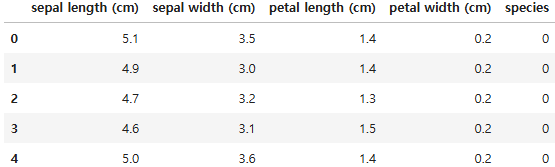
데이터 시각화로 보기
우선 어떤 변수가 품종을 잘 구분하는지 확인해보자.
boxplot
import matplotlib.pyplot as plt
plt.figure(figsize=(10,6))
sns.boxplot(x='petal length (cm)', y='species', data=iris_df, orient = 'h')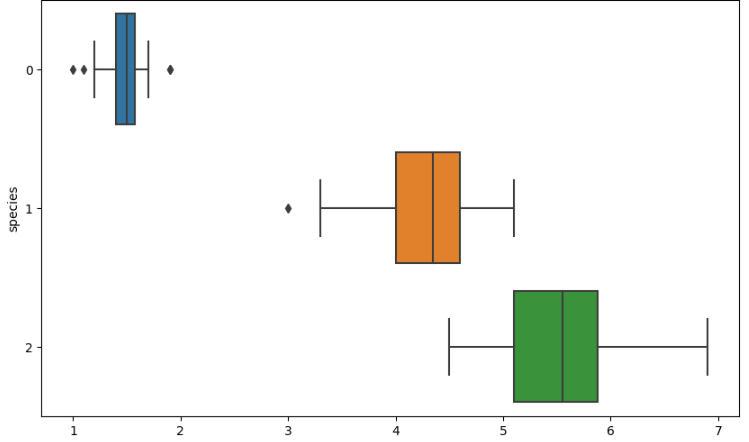
꽃잎의 길이(petal length)가 종을 비교적 잘 구분해준다.
pairplot
petal length가 비교적 잘 구분하는것으로 보이지만 확신할 수는 없다. pairplot을 이용해 자세히 살펴보자
import seaborn as sns
sns.pairplot(iris_df,hue='species')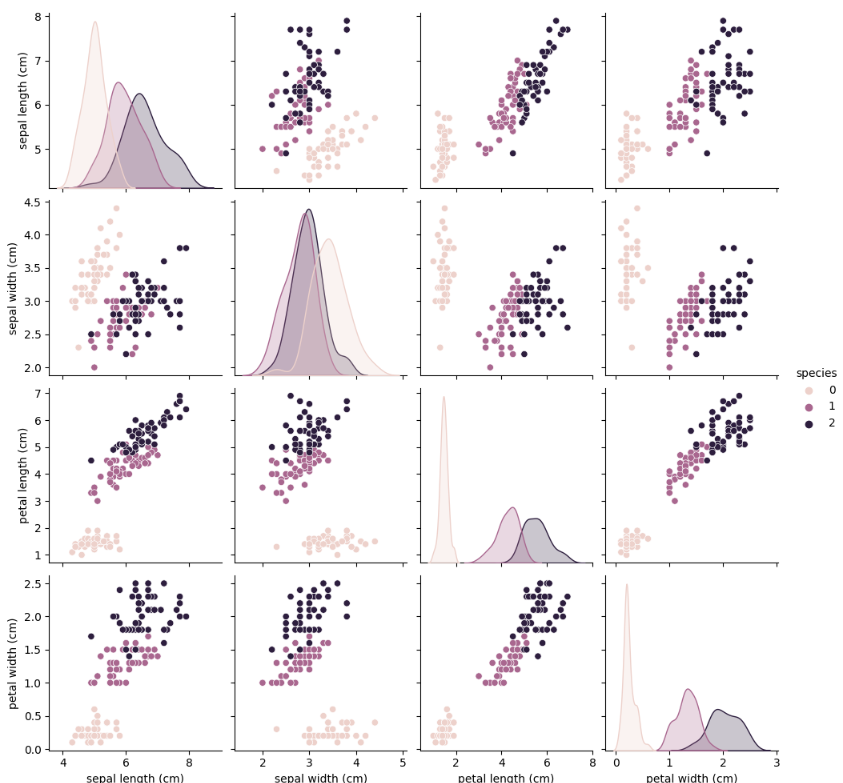
전체 변수 조합을 보면, 특히 petal length와 petal width 조합에서 종이 뚜렷하게 구분되는 것을 알 수 있다.
sns.pairplot(data = iris_df,
vars = ['petal length (cm)', 'petal width (cm)'],
hue = 'species', height = 4
)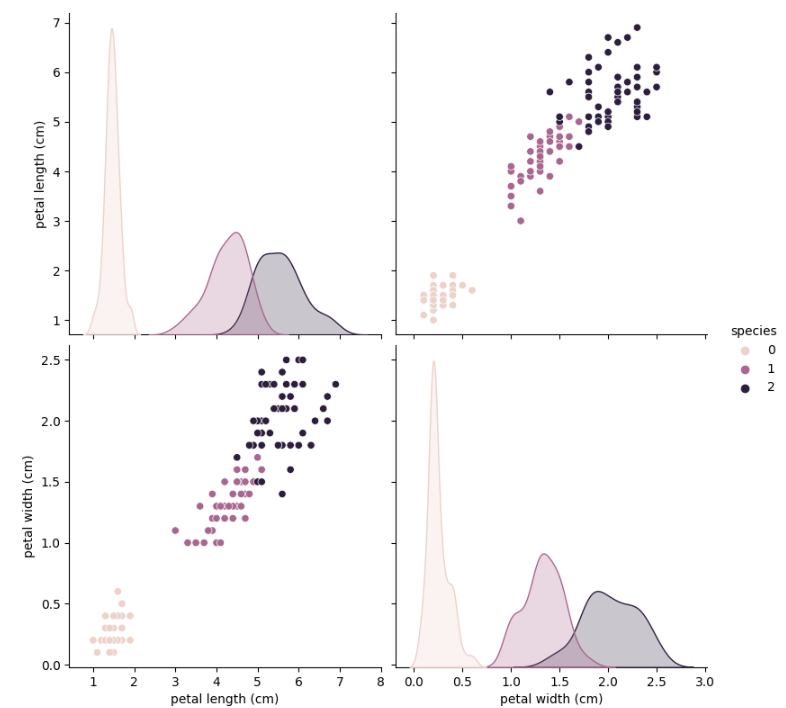
두 변수만으로도 충분히 분류가 가능해 보인다.
의사결정 나무
앞선 데이터에서 세 종을 구분하기 위해 데이터에 대한 구분 기준을 두고 각 종에 대한 구분을 할 수 있지 않을까? 아마 시각적으로 표현한다면 다음과 같을 것이다.
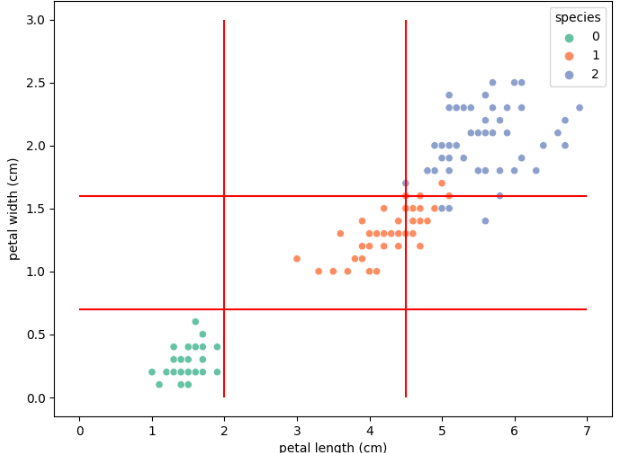
이때, 'petal length가 2.5보다 작고 peal width가 0.7보다 작을 때 Setosa로 분류한다'와 같은 규칙을 만들어 분류하는 것을 의사결정 나무라고 한다.
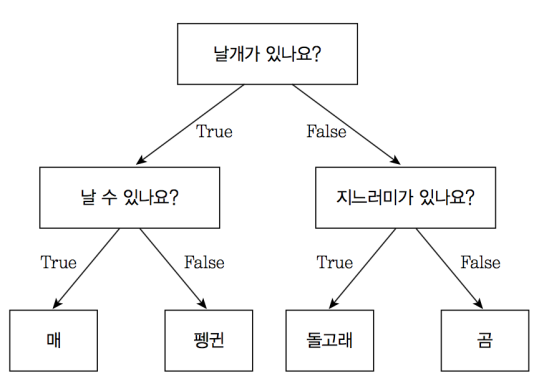
최적의 구분선 (Split Criterion) 찾기
그렇다면, 어떤 기준으로 분기점을 정할까? 대표적인 방법은 엔트로피(Entropy) 와 지니지수(Gini Index) 이다.
엔트로피
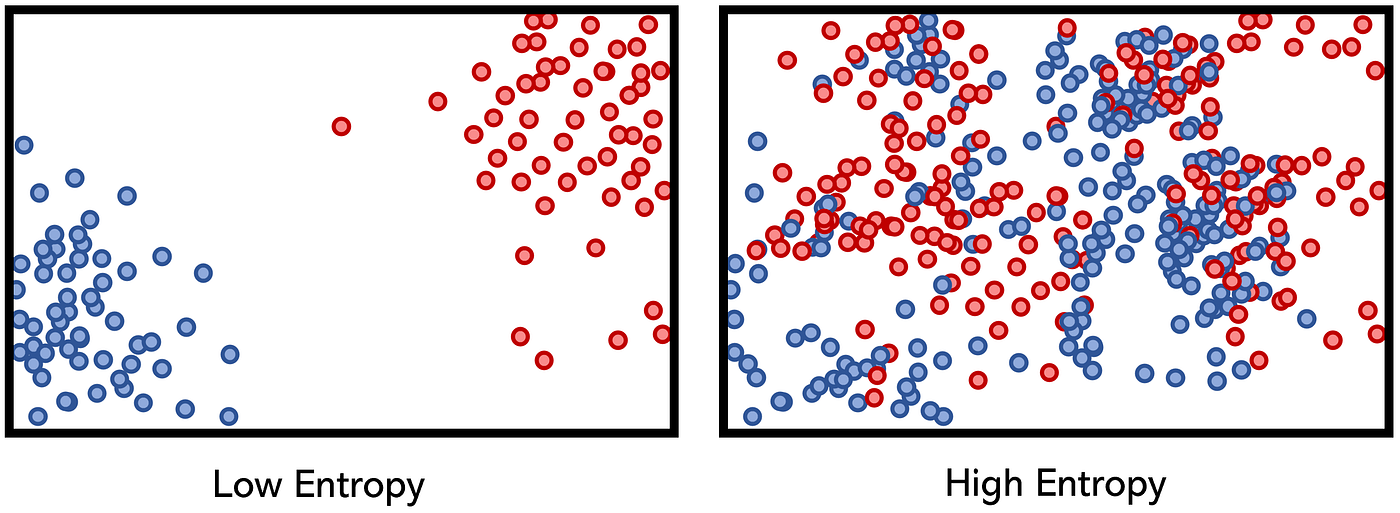
엔트로피는 데이터가 얼마나 섞여 있는지(무질서한지) 를 나타낸다.
공식은 다음과 같다
- p: 해당 사건의 확률
예시1: 예시: 빨간공 10개, 파란공 6개
예시 2: 공을 8개씩 두 그룹으로 나누었을 때 한 그룹에는 빨간공 7개와 파란공 1개, 다른 그룹에는 빨간공 3개와 파란공 5개가 있는 경우 계산
- R: 해당 그룹의 표본크기
엔트로피 값이 낮을수록 데이터가 잘 구분된 것이다.
지니지수
엔트로피와 비슷하지만 로그를 사용하지 않고 계산이 단순하다.
프레임워크를 활용한 최적의 지니지수 찾기
모든 기준에 대한 찾는 것은 매우 번거롭다. scikit-learn을 이용해 의사결정나무에서 최적의 구분기준을 찾고 쉽게 의사결절나무를 모델링 할 수 있다.
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
# 의사결정나무 모델 생성 (criterion, max_depth 등 설정 가능)
iris_tree = DecisionTreeClassifier()
# 학습 (petal length, petal width만 사용)
iris_tree.fit(iris.data[:,2:], iris.target)
# 학습 데이터 예측
y_pred_tr = iris_tree.predict(iris.data[:, 2:])
# 정확도 계산
acc = accuracy_score(iris.target, y_pred_tr)
print(acc)Accuracy: 0.9933333
