


💡 문제
십자가는 가운데에 '*'가 있고, 상하좌우 방향으로 모두 같은 길이의 '*'가 있는 모양이다. 십자가의 크기는 가운데를 중심으로 상하좌우 방향으로 있는 '*'의 개수이다. 십자가의 크기는 0보다 크거나 같아야 한다.
아래 그림은 크기가 0, 1, 2, 3인 십자가이고, 빈 칸은 '.'이다.

십자가의 넓이는 포함된 '*'의 개수이다. 크기가 0, 1, 2, 3인 십자가의 넓이는 1, 5, 9, 13이다.
크기가 N×M이고, '.'과 '#'로 이루어진 격자판이 주어진다. 격자판에 두 개의 십자가를 겹치지 않게 놓으려고 한다. 십자가는 '#'가 있는 칸에만 놓을 수 있다. 놓인 십자가 넓이의 곱의 최댓값을 구해보자.
입력
첫째 줄에 격자판의 크기 N, M (2 ≤ N, M ≤ 15)이 주어진다. 둘째 줄부터 N개의 줄에 격자판의 상태가 주어진다. 항상 두 개의 십자가를 놓을 수 있는 경우만 입력으로 주어진다.
출력
첫째 줄에 놓은 십자가 넓이의 곱의 최댓값을 출력한다.
💭 접근
이 문제는 십자가를 놓을 수 있는 두개의 지점(#)을 뽑아 놓을 수 있는 십자가의 최대 크기를 놓고, 두 십자가의 넓이의 곱을 구하는 문제로, 이 문제를 해결하기 위해서 다음과 같은 순서를 따른다.
1. 먼저 십자가를 놓을 수 있는 지점의 좌표를 저장한다.
blank_pos = []
for i in range(n):
for j in range(m):
if graph[i][j] == '#':
blank_pos.append([i, j])2. 위에서 저장한 좌표중 2개를 뽑아 십자가를 놓아본다. 이때 2개만 뽑으면 되므로 간단한 2중 for문으로 구현하였다.
for i in range(len(blank_pos) - 1):
for j in range(i + 1, len(blank_pos)):
cross1_x, cross1_y = blank_pos[i]
cross2_x, cross2_y = blank_pos[j]3. 이제 십자가를 놓을 좌표를 뽑았다면, 십자가의 크기를 조절하며 정답을 갱신하면 된다. 이때 순서는 먼저 하나의 십자가의 크기를 0으로 두고, 나머지 십자가의 크기를 조금씩 늘리며 해당 좌표에서 놓을 수 있는 십자가의 크기의 조합을 모두 놓아보면 된다.
이를 그림으로 나타내면 다음과 같다. 예시는 문제에서 주어진 예시 2번을 보자.
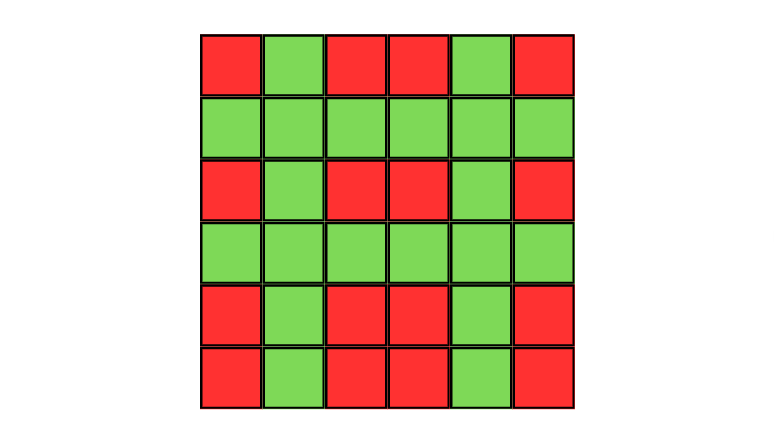
초록색 칸은 십자가를 놓을 수 있는 위치(#)이고, 빨간색 칸은 십자가를 놓을 수 없는 위치(.)이다. 현재는 아무 십자가도 놓여지지 않은 상태이다.
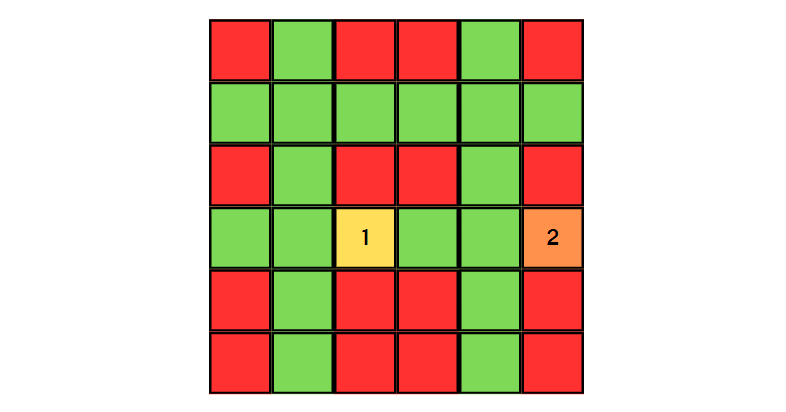
이때 2중 for문을 돌아 다음 위치에 도달했다고 가정해보자. 노란색은 십자가 1, 주황색은 십자가 2이다.

이 현재 십자가 1과 십자가 2의 크기는 각각 0으로 동일하다. 이제 앞서 말했듯이 십자가 1에 따라 십자가 2의 크기를 늘리며 넓이를 구해보자.
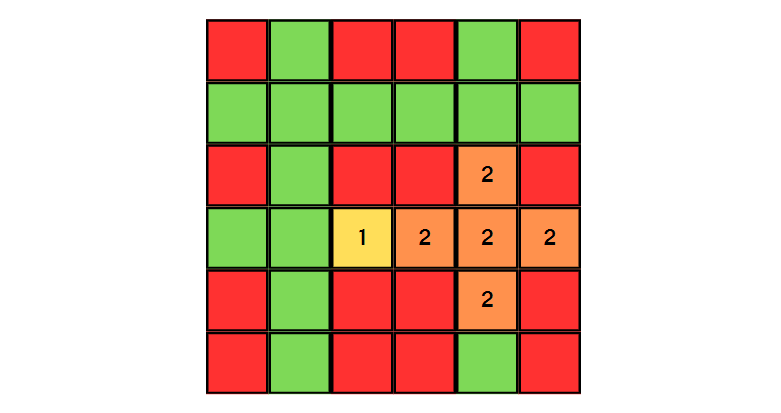
십자가 2를 최대로 늘리면 크기가 1이고, 이들의 곱은 1 x 5 = 5로 5가 된다.
이후, 십자가 2의 크기를 다시 0으로 초기화하고 십자가 1의 크기를 늘릴 차례인데 더이상 늘릴 수 없으므로 다음 좌표의 조합을 뽑아 진행한다.
이렇게 순회하게 되면 결국 정답이 될 수 있는 경우의 수 중 하나를 다음과 같이 구할 수 있다.
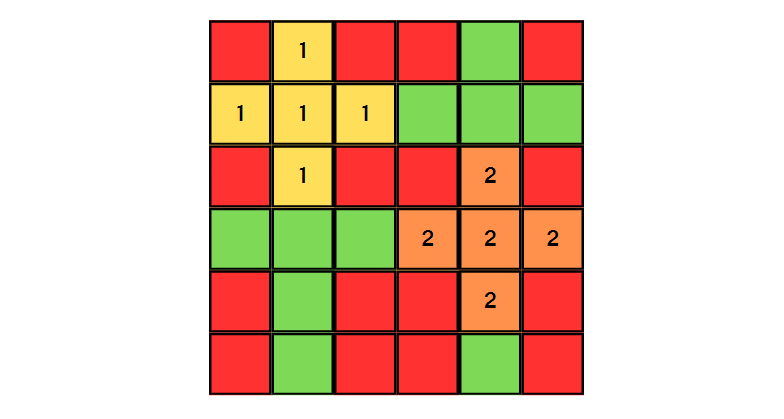
따라서 모든 좌표의 조합에서 놓을 수 있는 모든 크기의 십자가를 놓아보며 넓이의 곱의 최대를 구하면 되는 문제이다.
📒 코드
def can(cross_x, cross_y, cross_len):
for i in range(4):
nx = cross_x + dx[i] * cross_len
ny = cross_y + dy[i] * cross_len
if 0 <= nx < n and 0 <= ny < m and tmp[nx][ny] == '#':
pass
else:
return False
return True
def draw(cross_x, cross_y, cross_len):
for i in range(4):
for j in range(cross_len + 1):
nx = cross_x + dx[i] * j
ny = cross_y + dy[i] * j
tmp[nx][ny] = '*'
n, m = map(int, input().split())
graph = [list(input()) for _ in range(n)]
blank_pos = []
for i in range(n):
for j in range(m):
if graph[i][j] == '#':
blank_pos.append([i, j])
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
ans = 0
for i in range(len(blank_pos) - 1):
for j in range(i + 1, len(blank_pos)):
cross1_x, cross1_y = blank_pos[i]
cross2_x, cross2_y = blank_pos[j]
for cross1_len in range(16):
tmp = [graph[k][:] for k in range(n)]
tmp[cross1_x][cross1_y] = '*'
tmp[cross2_x][cross2_y] = '*'
if cross1_len == 0 or can(cross1_x, cross1_y, cross1_len):
draw(cross1_x, cross1_y, cross1_len)
else:
break
for cross2_len in range(16):
if cross2_len == 0 or can(cross2_x, cross2_y, cross2_len):
draw(cross2_x, cross2_y, cross2_len)
ans = max(ans, (4 * cross1_len + 1) * (4 * cross2_len + 1))
else:
break
print(ans)💭 후기
간단한 조합 문제였지만 십자가를 놓고, 그 크기를 조절하는 데에 약간의 구현이 섞여있어 까다로웠던 문제였다.
🔗 문제 출처
https://www.acmicpc.net/problem/17085
