


💡 문제
2차원 평면상에 n개의 점이 주어졌을 때, 이 점들 중 가장 가까운 두 점을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 자연수 n(2 ≤ n ≤ 100,000)이 주어진다. 다음 n개의 줄에는 차례로 각 점의 x, y좌표가 주어진다. 각각의 좌표는 절댓값이 10,000을 넘지 않는 정수이다. 여러 점이 같은 좌표를 가질 수도 있다.
출력
첫째 줄에 가장 가까운 두 점의 거리의 제곱을 출력한다.
💭 접근
이 문제는 이분 탐색 방식으로 x좌표 기준 왼쪽 영역과 오른쪽 영역을 나누어 각각의 영역에서 최소 거리를 구한 뒤, 합치면서 최소 거리를 계속 갱신하며 문제를 해결할 수 있다.
그러나, 이 문제에서 한가지 주의해야할 점이 있는데, 왼쪽 오른쪽 각각의 영역에서 구한 최소 거리가 정답과 다를 수 있다는 점이다.
아래 그림을 보며 살펴보자.
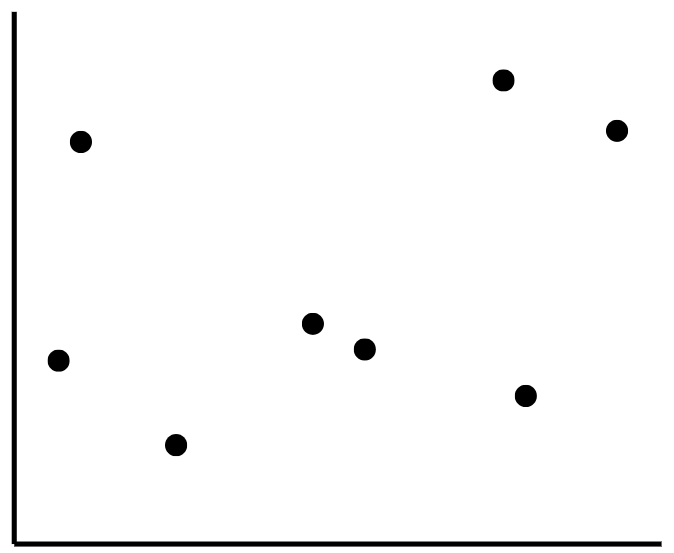
먼저 위와 같은 그림이 있다고 가정해보자.
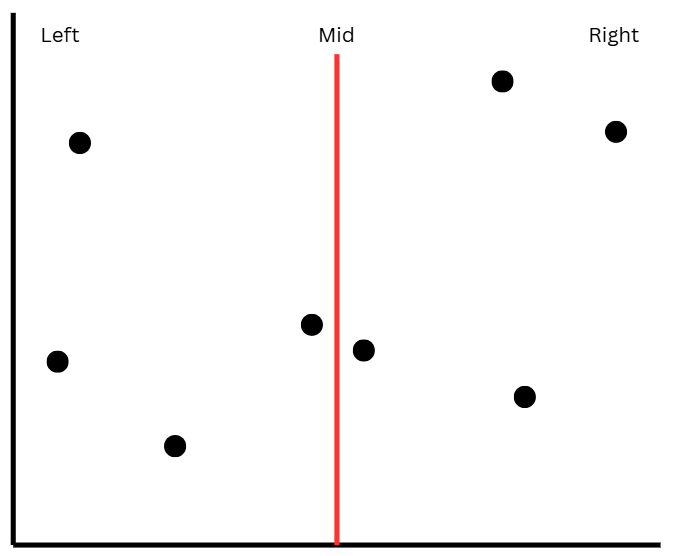
이제 이분 탐색 방식으로 영역을 나누어 각 영역에서의 최소 거리를 구한다. 이때 그림에서 볼 수 있듯이 만약 Mid가 최소 거리를 이루는 두 점 사이를 가로지른다면 이 두 점 사이의 거리는 비교할 수 없게된다.
따라서 각 영역에서 최소 거리를 구한 뒤, 추가적인 계산을 해주어야한다.
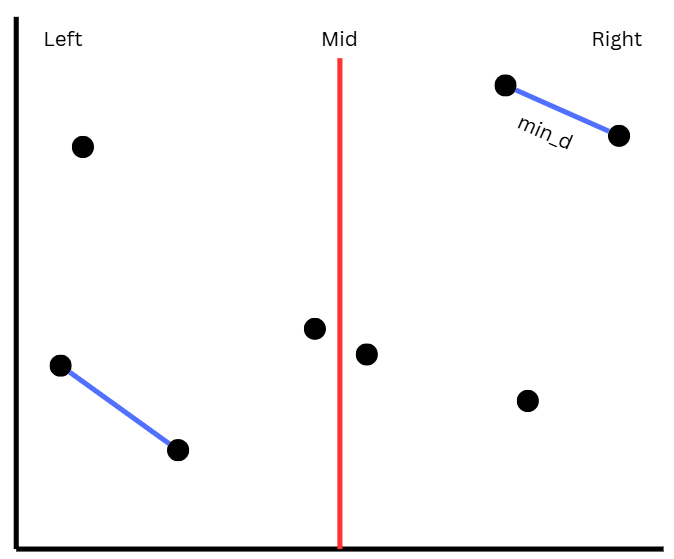
일단 각 영역에서의 최소 거리를 구한다. 위 그림에서는 오른쪽 영역의 최소 거리가 왼쪽 영역의 최소 거리보다 짧다.
따라서 mid_d는 오른쪽 영역의 최소 거리가 된다.
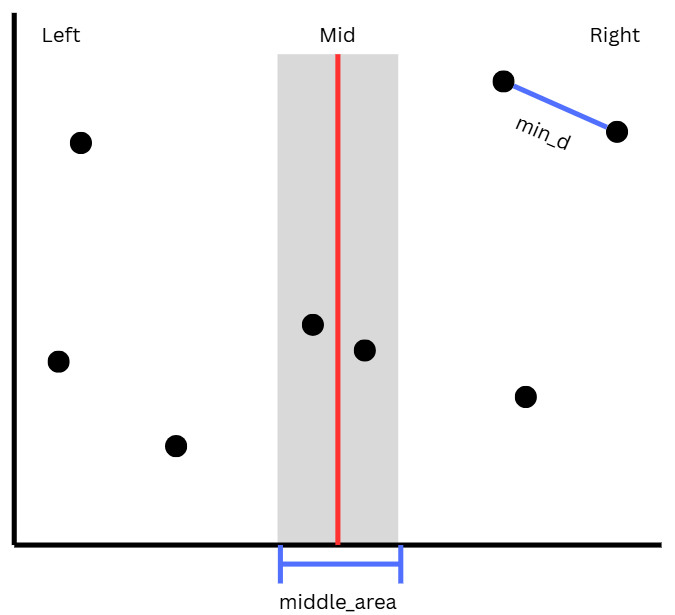
이제 중간 영역에 있는 점들 또한 고려하기 위해 Mid를 기준으로 min_d보다 거리가 짧은 점이 있는지 탐색해 주어야한다.
middle_area.sort(key=lambda x: x[1])
for i in range(len(middle_area) - 1):
for j in range(i + 1, len(middle_area)):
if (middle_area[i][1] - middle_area[j][1]) ** 2 < min_d:
d = dist(middle_area[i][0], middle_area[i][1],
middle_area[j][0], middle_area[j][1])
min_d = min(min_d, d)
else:
break이 과정을 거치게 되면 중간 영역에 있는 점들까지 모두 고려할 수 있게 되고, 따라서 아래 그림과 같이 더 짧은 거리를 이루는 두 점을 찾을 수 있게 된다.
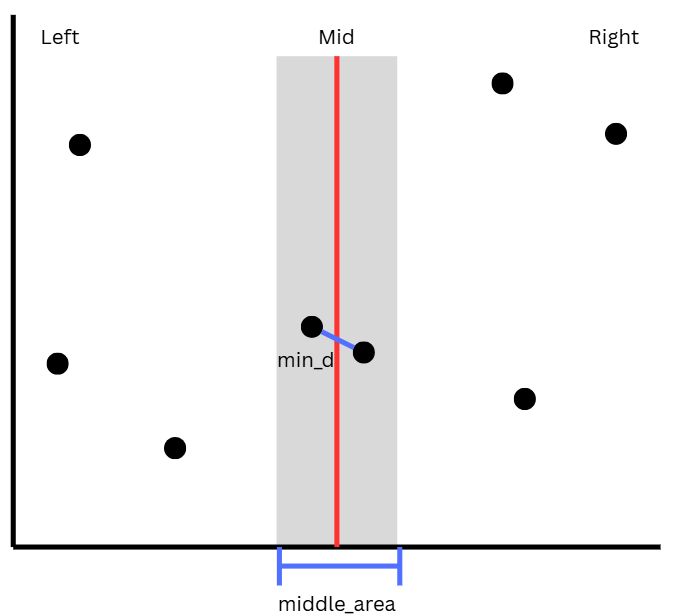
정리하자면,
- 먼저 주어진 영역을 두개로 나눈다.
- 각 영역에서 최소 거리를 구한 뒤, 두 값을 비교하여 하나의 최소 거리를 구한다.
- Mid를 기준으로 위 단계에서 구한 최소 거리보다 짧은 거리를 이루는 점이 있는지 탐색한다.
- 위 과정을 반복한다.
📒 코드
def dist(x1, y1, x2, y2):
return (x1 - x2) ** 2 + (y1 - y2) ** 2
def find_closest_dot(left, right):
if left == right:
return 1e10
else:
mid = (left + right) // 2
min_d = min(find_closest_dot(left, mid), find_closest_dot(mid + 1, right))
middle_area = []
for i in range(mid, left - 1, -1):
if (dots[i][0] - dots[mid][0]) ** 2 < min_d:
middle_area.append(dots[i])
else:
break
for i in range(mid + 1, right + 1):
if (dots[i][0] - dots[mid][0]) ** 2 < min_d:
middle_area.append(dots[i])
else:
break
middle_area.sort(key=lambda x: x[1])
for i in range(len(middle_area) - 1):
for j in range(i + 1, len(middle_area)):
if (middle_area[i][1] - middle_area[j][1]) ** 2 < min_d:
d = dist(middle_area[i][0], middle_area[i][1], middle_area[j][0], middle_area[j][1])
min_d = min(min_d, d)
else:
break
return min_d
n = int(input())
dots = []
for _ in range(n):
x, y = map(int, input().split())
dots.append((x, y))
dots.sort()
if len(dots) != len(set(dots)):
print(0)
else:
print(find_closest_dot(0, len(dots) - 1))💭 후기
가장 가까운 두 점을 찾는 알고리즘은 매우 잘 알려져 있는 알고리즘으로, 문제를 풀 땐 많이 까다로웠지만 풀이를 보면 빠르게 이해할 수 있었다.
🔗 문제 출처
https://www.acmicpc.net/problem/2261
