[백준] 7562번 나이트의 이동 - Python / 알고리즘 기초 2/2 - 그래프 1

---

---

---

💡 문제

체스판 위에 한 나이트가 놓여져 있다. 나이트가 한 번에 이동할 수 있는 칸은 아래 그림에 나와있다. 나이트가 이동하려고 하는 칸이 주어진다. 나이트는 몇 번 움직이면 이 칸으로 이동할 수 있을까?

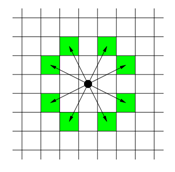
입력

입력의 첫째 줄에는 테스트 케이스의 개수가 주어진다.

각 테스트 케이스는 세 줄로 이루어져 있다. 첫째 줄에는 체스판의 한 변의 길이 l(4 ≤ l ≤ 300)이 주어진다. 체스판의 크기는 l × l이다. 체스판의 각 칸은 두 수의 쌍 {0, ..., l-1} × {0, ..., l-1}로 나타낼 수 있다. 둘째 줄과 셋째 줄에는 나이트가 현재 있는 칸, 나이트가 이동하려고 하는 칸이 주어진다.

출력

각 테스트 케이스마다 나이트가 최소 몇 번만에 이동할 수 있는지 출력한다.

---

💭 접근

2178번 미로 탐색 문제와 유사하지만 체스의 나이트의 이동방법처럼 움직일 수 있고, 목표 지점에 도달했을 때 탐색을 멈추고 값을 return 해주어야 한다.

우선, 나이트의 이동 방법처럼 dx, dy를 다음과 같이 저장하였다.

dx = [-2, -1, 1, 2, 2, 1, -1, -2]
dy = [1, 2, 2, 1, -1, -2, -2, -1]
# 1시 방향부터 시계방향으로

이후, BFS 함수에서 큐에 저장되어 있는 나이트의 좌표값을 꺼낼때, 목표 좌표와 같다면 탐색을 중단하고 그 값을 return 해준다.

---

📒 코드

from collections import deque

def bfs(x, y):
    q = deque()
    q.append((x, y))

    while True:
        x, y = q.popleft()
        if x == end_x and y == end_y:
            return graph[x][y]

        dx = [-2, -1, 1, 2, 2, 1, -1, -2]
        dy = [1, 2, 2, 1, -1, -2, -2, -1]

        for i in range(8):
            nx = x + dx[i]
            ny = y + dy[i]

            if 0 <= nx < l and 0 <= ny < l and graph[nx][ny] == 0:
                graph[nx][ny] = graph[x][y] + 1
                q.append((nx, ny))

t = int(input())

for _ in range(t):
    l = int(input())
    graph = [[0 for _ in range(l)] for _ in range(l)]
    start_x, start_y = map(int, input().split())
    end_x, end_y = map(int, input().split())

    print(bfs(start_x, start_y))

---

💭 후기

dx, dy로 탐색 방향을 자유자재로 바꿀 수 있다는 점이 재밌었다.

---

🔗 문제 출처

https://www.acmicpc.net/problem/7562

---