Recurrent Neural Network(RNN)

chchch·2021년 4월 10일

DL NLP

DL

목록 보기

1/2

최근 "seq2seq(sequence-to-sequence)"를 공부할 기회가 생겼다. 그래서 자연어처리에 사용하는 neural network 모형 중 기본이 되는 RNN을 정리해보았다.

1. 언어모델(Language Model)

언어 모델은 단어 나열(sequence) 혹은 문장에 확률을 부여한다. 다음과 같이 단어의 나열을 생각해 볼 수 있다.

x^{(1)}, x^{(2)}, \dots, x^{(m)}

여기서 $x^{(t)}, t=1,\dots,m$ 는 단어를 의미한다.

예를 들어 "나는 밥을 먹는다"에서 띄어쓰기로 단어를 구분한다는 가정하에 $x^{(1)}$ ="나는", $x^{(2)}$ ="밥을", $x^{(3)}$ ="먹는다"로 대응시킬 수 있다.

그리고 "나는 밥을 먹는다"와 같은 문장이 나올 확률을 정의할 수 있다. 물론 여기서 단어의 순서는 상관없고 단어들이 동시에 나오는 확률이라고 해서 "동시 확률"이라고 한다.

P(x^{(1)}, x^{(2)}, \dots, x^{(m)}) = P(x^{(2)}, x^{(1)}, \dots, x^{(m)}) =\cdots = P(x^{(m)}, x^{(m-1)}, \dots, x^{(1)})

그리고 위의 확률들을 확률의 곱셈정리에 의해 다음과 같이 표현이 가능하다.

P(x^{(1)}, x^{(2)}, \dots, x^{(m)}) = \prod_{t=1}^{m}P(x^{(t)} |x^{(1)},\dots, x^{(t-1)} )

언어모델 중 word2vec 방법들은 동시 확률을 이용해서 단어들의 임베딩 벡터를 학습했다. 임베딩 벡터 학습에는 큰 문제가 없을 수 있지만 만약 문장을 만드는 모델에서는 단어의 순서를 고려하지 않는다면 큰 문제가 발생할 수 있다. 따라서 단어의 순서를 고려할 수 있는 모델들을 고려하게 된다. 그 중에 하나가 바로 "RNN(Recurrent Neural Network)" 이다.

2. RNN(Recurrent Neural Network)

2.1 Recurrent?

RNN을 번역하면 순환신경망이라고 한다. 무엇이 순환하는건가? 바로 뒤에서 설명할 "은닉 상태(hidden state)" 가 신경망 모델에서 순환하게 된다. 먼저 그림을 통해 확인해보자.

그림 출처: "Audio visual speech recognition with multimodal recurrent neural networks(Feng et al, 2017)"

이제부터 bold 표기법은 모두 벡터를 의미한다.

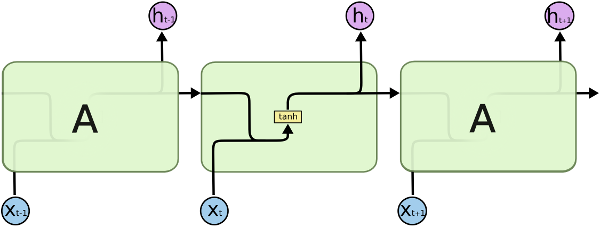
먼저 왼쪽 그림을 보면 입력값 $\textbf{x}$ 가 모델로 들어가서 계산을 통해 은닉 상태 $\textbf{h}$ 가 되는데 $\textbf{h}$ 는 다시 모델로 들어가도록 설계가 되어있는 것을 확인할 수 있다. 개인적으로 오른쪽에 있는 "Unfold 그림"을 더 선호하는데 그 이유가 모델을 펼쳐보면 이해가 잘 되기 때문이다.

$t$ 시점의 입력값 $\textbf{x}^{(t)}$ 이 신경망 모델로 들어가게 되는데 이때, $(t-1)$ 시점의 은닉 상태 $\textbf{h}^{(t-1)}$ 도 같이 모델로 들어가게 된다. 여기서 $\textbf{h}^{(t-1)}$ 는 이전 $(t-1)$ 시점에서 $\textbf{x}^{(t-1)}$ 과 $\textbf{h}^{(t-2)}$ 으로 만들어진 것이다. 즉, 이전 정보가 들어있는 은닉 상태이다. 바로 이전 시점의 은닉 상태가 입력값으로 들어오기 때문에 "이전의 정보" 가 사용되는 것이다. 물론 $\textbf{h}^{(t-1)}$ 은 바로 이전 $(t-1)$ 시점의 은닉 상태이긴하지만 이전 $(t-1),\dots, 1$ 시점들의 모든 정보를 포함하고 있다.

그리고 은닉(hidden)이라고 하는 이유는 모델에서는 계속 순환하지만 우리는 중간에 이 값을 확인하기가 어렵기 때문이라고 생각한다. 물론 코드를 통해서는 은닉 상태 값을 확인할 수 있다.

"순환" = "전달"

RNN에서는 '은닉 상태의 순환'을 통해 이전 정보를 다음 단계로 전달한다.

2.2 Vanilia RNN

먼저 위의 RNN 구조에서 $t$ 시점에 일어나는 계산을 알아보자.

$\textbf{h}^{(t)}$ 를 이전 $(t-1)$ 시점의 은닉 상태 $\textbf{h}^{(t-1)}$ 와 입력값 $\textbf{x}^{(t)}$ 의 함수로 표현할 수 있다.

\begin{aligned} \textbf{h}^{(t)} &= f_{\textbf{W, U}}(\textbf{h}^{(t-1)}, \textbf{x}^{(t)}) \\ &= tanh(\textbf{Wh}^{(t-1)}+\textbf{Ux}^{(t)} + \textbf{b}) \\ \end{aligned}

여기서 $\textbf{W}$ 와 $\textbf{U}$ 는 각각 은닉상태 $\textbf{h}^{(t-1)}$ 와 입력값 $\textbf{x}^{(t)}$ 랑 곱해지는 가중치 행렬이며 학습을 통해 구하는 모수(parameter)들이다. 절편 $\textbf{b}$ 도 마찬가지이다. $tahn$ 은 hyperbolic tangent 함수이다.

참고로 $t = 1$ 인 경우에도 $\textbf{h}^{(0)}$ 이 주어져야한다.

그리고 위의 그림에서 각 시점마다 출력값 $\textbf{o}$ 를 확인할 수 있다.

\textbf{o}^{(t)} = \textbf{V}\textbf{h}^{(t)} + \textbf{c}

여기서, $\textbf{V}$ 와 $\textbf{c}$ 는 각각 가중치 행렬과 절편 벡터이고 마찬가지로 학습을 통해 구하는 모수들이다.

그렇다면 이제 출력값을 통해 손실함수(loss function)을 계산할 수 있다. 손실함수를 계산하기 위해서 실제 $t$ 시점에서 정답인 $\textbf{y}^{(t)}$ 를 가정하자. $t$ 시점에서의 손실함수를 $L^{(t)}$ 라고 정의하고 평균오차제곱합(Mean Squared Error)이라고 가정하자. 그렇다면 RNN 모델의 총 손실함수 L은 다음과 같이 정의된다.

\begin{aligned} L &= \sum_{t=1}^{m} L^{(t)} \\ &= \sum_{t=1}^{m} (\textbf{y}^{(t)} -\textbf{o}^{(t)})^\top (\textbf{y}^{(t)} -\textbf{o}^{(t)}) /n \end{aligned}

여기서 $n$ 은 $\textbf{y}^{(t)}$ 와 $\textbf{o}^{(t)}$ 의 차원이다.

예를 들어 A기업의 주식가격 $(\in \mathbb{R})$ 예측을 RNN으로 한다고 하자. 그러면 우리는 $t$ 시점의 정보 $\bf{x}^{(t)}$ 를 가지고 $y^{(t)}$ 를 맞추고 싶을 것이다. 그리고 $t$ 시점의 손실함수 $L^{(t)}$ 는 예측 가격 $o^{(t)}$ 과 실제 가격 $y^{(t)}$ 차이의 제곱이 된다. 총 손실함수 L은 차이의 제곱합이 된다.

물론 꼭 시점마다 출력값이 나올 필요는 없다. 모델 설계에 따라 달라진다. 마지막 시점에 최종 출력값만 나오는 경우에는 총 손실함수의 계산이 시점의 손실함수의 합으로 표현되지 않는다.

최종적으로는 RNN 모델은 손실함수를 줄이는 모수들을 계속해서 찾도록 학습을 진행할 것이다.

2.3 Vanilia RNN with Likelihood Function

자연어 처리 분야(Natural Language Process; NLP)에서는 출력물 $\bf{o}^{(t)}$ 을 정규화되지 않은 로그확률(unnormalized log probability)로 생각할 수 있다. 출력물 $\bf{o}^{(t)}$ 이 $n$ 차원의 벡터 $(\bf{o}^{(t)} \in \mathbb{R}^n)$ 이면 $\bf{o}^{(t)}$ 의 각 원소(element)들은 원소와 대응하는 단어가 발생할 로그확률값이 된다.

정규화되지 않은 로그확률(unnormalized log probability)

위의 단어는 Ian Goodfellow가 쓴 "Deep Learning" 책의 내용을 인용한 것이다. 로그확률값은 확률값과 $log$ 가 동시에 정의되는 $(0,1]$ 서포트에서는 $log$ 값은 0 이하의 값을 갖는다. 하지만 $\bf{o}^{(t)}$ 을 로그확률로 생각하자고 했지만 모델 어디에도 $\bf{o}^{(t)} \leq 0_{n\times1}$ 에 대한 제약조건은 없다. 학습과정에서는 $\bf{o}^{(t)}$ 의 원소값들이 $0$ 이하의 값을 갖는다고 보장할 수 없다. 이 부분이 마음에 걸려서 구글링을 해본 결과 비슷한 생각을 한 사람들이 생각을 공유한 글이 있어서 첨부한다[1]. 저 글을 통해서 보면 다음과 같이 쓰는게 더 맞는 표현인것 같다. "log of unnormalized probabililty".

예를 들어 처음 들었던 예시를 이용해보겠다. "나는 밥을 먹는다" 시점마다 문장의 감성을 알고 싶다. 감성이 "긍정", "부정", "중립" $3$ 가지만 있다고 가정을하면 $3$ 차원 벡터 $\bf{o}^{(t)}$ 를 다음과 같이 표현할 수 있다.

\begin{aligned} \textbf{o}^{(t)}&=(o^{(t)}_1, o^{(t)}_2, o^{(t)}_3)^\top \\ &= (\log p(\text{긍정}|\textbf{h}^{(t)}), \log p(\text{중립}|\textbf{h}^{(t)}), \log p(\text{부정}|\textbf{h}^{(t)}))^\top \end{aligned}

여기서, $o^{(t)}_i, i=1,2,3$ 이고 각각 $t$ 시점에서 "긍정", "부정", "중립" 감성과 대응되는 로그확률이다.

출력값이 이해되기 쉽고 확률처럼 와닿게 하기 위해서는 단계가 하나 더 필요하다. 바로 "softmax" 단계이다. $t$ 시점에서 $i$ 번째 단어의 로그확률값 $(o^{(t)}_i)$ 은 softmax를 거치면 $\hat{y}^{(t)}_i \in [0,1]$ 을 값을 갖고 모든 $i$ 에 대해서 합을 구해보면 $1$ 이 된다. 마치 확률처럼.

\hat{y}^{(t)}_i = softmax(o^{(t)}_i) = \frac{exp(o^{(t)}_i)}{\sum_{j=1}^{n}exp(o^{(t)}_j)}

모든 $i$ 에 대해서 $\hat{y}^{(t)}_i$ 합을 구하면 $1$ 이 된다는 것을 쉽게 확인할 수 있다.

이제 단어의 발생확률이 출력값이 되었으니 그에 걸맞는 손실함수도 새롭게 정의해보자. 출력값이 확률인 경우에는 다양한 손실함수를 정의할 수 있지만 통계학에서 사용하는 가능도함수(likelihood function)도 고려할 수 있다. 학부 때 수업에서 들었던 내용이 맞다면 "통계학의 아버지"라고 불리는 R.A. Fisher가 제안했다. 가능도함수는 통계학에서 가장 중요한 개념 중에 하나이다(추정, 검정 등). 기회가 된다면 가능도함수에 대해 더 자세하게 글을 쓰고 싶지만 여기서는 통계 비전공자를 위해 간략하게 소개하겠다.

가능도함수(likelihood function)

가능도함수는 말 그래도 확률변수들의 가능도를 나타내는 함수이다. 즉, 클수록 가능성도 큰 것이다. 그럼 가능도랑 확률이랑 다른 것인가? 확률은 $[0,1]$ 의 값을 갖지만 가능도는 그렇지 않아도 된다.
$n$ 개의 확률변수 $\textbf{X}=(X_1, \dots, X_n)$ 가 $\textbf{x} =(x_1, \dots, x_n)$ (데이터)로 관측됐을 경우, 가능도함수 $L$ 은 다음과 같이 정의한다.
$L(\theta;\textbf{x}) = P(\textbf{X}=\textbf{x};\theta)=\prod_{i}^{n}p(x_i;\theta)$
위의 식을 보면 가능도함수는 모수(parameter), 여기서는 $\theta$ 의 함수이다. 따라서 우리는 관측된 데이터의 가능도를 가장 크게 해주는 모수 $(\theta)$ 를 구하고 싶어하는 것이다. 가능성이 가장 높기 때문에 관측됐을 거라는 믿음이 전제된다. 예를 들면, 동전을 10000번 던졌는데 앞면이 7000번 나오면 앞면이 나올 확률( $\theta$ )를 0.7로 생각할 것이다. 이 방법을 "최대가능도추정법(Maximum Likelihood Estimation)", 줄여서 "MLE" 라고 한다.

위의 가능도함수는 일반적으로 확률밀도함수(PDF)들의 곱으로 나타내는데 $log$ 를 취하면 확률밀도함수들의 합으로 표현되기 때문에 로그가능도함수를 많이 사용한다. 중요한 것은 가능도를 최대화하는 것인데 $log$ 도 단조증가하는 함수이기 때문에 대소관계는 유지된다. 근데 일반적으로 기계학습 분야에서는 최소화 문제로 최적화를 한다. 따라서 음의 로그가능도함수(negative log likelihood)를 최소화한다. 결국 가능도를 최대화하는 것이다.

가능도에 대한 얘기가 길었다. 다시 돌아와서 RNN 모델의 손실함수를 음의 로그가능도함수로 다음과 같이 정의할 수 있다.

L(\textbf{W}, \textbf{U}, \textbf{V}, \textbf{b}, \textbf{c})=\sum_t L^{(t)} = -\sum_t \log p(y^{(t)}, \textbf{x}^{(1)},\dots,\textbf{x}^{(t)} ; \textbf{W}, \textbf{U}, \textbf{V}, \textbf{b}, \textbf{c})

여기서, $y^{(t)}$ 는 실제 정답이다.

"나는 밥을 먹는다"에서 각 시점에서의 감성은 $(y^{(1)}, y^{(2)},y^{(3)})=$ (중립, 중립, 긍정)이라고 하자. 그러면 음의 로그가능도함수는 다음과 같이 계산할 수 있다.

\begin{aligned} L(\textbf{W}, \textbf{U}, \textbf{V}, \textbf{b}, \textbf{c}) &=-\log p(\text{중립, 나는}; \textbf{W}, \textbf{U}, \textbf{V}, \textbf{b}, \textbf{c}) \\ & -\log p(\text{중립, 나는, 밥을}; \textbf{W}, \textbf{U}, \textbf{V}, \textbf{b}, \textbf{c})\\ & -\log p(\text{긍정, 나는, 밥을, 먹는다}; \textbf{W}, \textbf{U}, \textbf{V}, \textbf{b}, \textbf{c}) \end{aligned}

결국에는 아래와 같이 계산을 할 것이다.

\begin{aligned} L(\textbf{W}, \textbf{U}, \textbf{V}, \textbf{b}, \textbf{c}) &= -\sum_t \log \hat{y}^{(t)}_c \\ &= -\log\hat{y}^{(1)}_2 - \log\hat{y}^{(2)}_2 - \log\hat{y}^{(3)}_3 \end{aligned}

여기서, $\hat{y}^{(t)}_c$ 는 실제 $t$ 시점 정답 $y^{(t)}$ 에 대응되는 $\hat{y}^{(t)}_i$ 이다.

결국 손실함수는 가중치 행렬 $(\textbf{W}, \textbf{U}, \textbf{V})$ 들과 절편 벡터 $(\textbf{b}, \textbf{c})$ , 즉 모수들에 대한 식으로 쓰여진다. 그리고 손실함수를 줄여나가면 정답이 나올 가능성을 가장 크게 해주는 가중치행렬과 절편 벡터들을 찾을 수 있다. 결국 통계학에서 많이 사용하는 "최대가능도추정법"과 연결되는 것이다.

다음 포스팅에서는 LSTM에 대해서 다루겠다.

References

사이토 고키, 밑바닥부터 시작하는 딥러닝2, 한빛미디어.
Ian Goodfellow et al., Deep Learning, MIT Press, Book website.
Zhang et al., Dive into Deep Learning, Book website.

chchch

머신러닝과 통계학을 공부하는 사람

다음 포스트