Variational Inference(변분 추론)

chchch·2021년 4월 12일

ML

목록 보기

1/2

VAE의 근본이 되는 "variational inference(=variational bayes)"에 대해서 정리를 하고자 한다. 이 포스팅은 Christopher Bishop의 'Pattern Recognition and Machine Learning' 책의 내용을 바탕으로 작성했다.

Variational Inference

먼저, 추론의 목적은 데이터의 가능도(likelihood)를 계산하는 것이고 그리고 잠재변수(latent variable)의 사후확률분포(posterior distribution), $p({\bf Z}|{\bf X})$ 를 구하는 것이다. 하지만 정확한 분포를 알지 못하므로 사실상 불가능한 문제이다. 그래서 추론을 최적화 문제로 바꿔서 최대한 비슷한 값을 구하고자 한다. 데이터 $\bf X$ 가 있을 때, 데이터의 로그-주변부(marginal) 확률분포는 다음과 같이 쓸 수 있다.

\begin{aligned} \log p({\bf X}) &=\int q({\bf Z})\log \frac{p({\bf X}, {\bf Z})}{q({\bf Z})} \text{d}{\bf Z} - \int q({\bf Z})\log \frac{p({\bf Z} | {\bf X})}{q({\bf Z})} \text{d}{\bf Z} \\ & = \mathcal{L}(q) + \text{KL}(q({\bf Z})\| p({\bf Z}|{\bf X})) \end{aligned}

여기서 $\bf Z$ 는 잠재 변수이고 q( $\cdot$ )는 우리가 다룰 수 있는 혹은 계산할 수 있는(tractable) $\bf Z$ 를 확률변수로 갖는 임의의 확률분포이다.

위의 식에서 앞 항, $\mathcal{L}(q)$ 을 많은 책에서 ELBO(Evidence Lower Bound) 혹은 Variational Free Energy라고 한다. 뒤의 항은 분포간의 유사도(?)의 측도로 쓰일 수 있는 KL-divergence이다. 위의 식에서 $\log p({\bf X})$ 가 고정이고 ELBO를 최대화하는 것은 KL-divergence를 최소화하는 것과 동일해진다. 이 흐름은 처음의 추론의 목적과 연결된다. KL-divergence가 줄어든다는 것은 사후확률분포와 $q({\bf Z})$ 이 유사해지는 것이다. 우리가 알지 못하는 사후확률분포를 그에 가까워진 $q({\bf Z})$ 를 통해서 추론한다. 이처럼 $q({\bf Z})$ 를 도입해서 ELBO를 최대화함으로써 계산불가능한 KL-divergence를 간접적으로 줄인다. 여기서, $q({\bf Z})$ 를 "variational distribution" 이라고 하고 위와 같은 방법을 "variational inference" 라고 한다.

위에서 $\mathcal{L}(q)$ 와 같이 함수를 정의역으로 갖는 함수를 수학에서 범함수(functional)라고 한다. 머신러닝에 많이 쓰이는 Shannon Entropy도 범함수이다.

Factorized Distributions

위의 ELBO, $\mathcal{L}(q)$ 를 최대화하기 위해서 variational distribution, $q({\bf Z})$ 에 제약을 둔다. $q({\bf Z})$ 가 서로 배반(disjoint)인 그룹인 $Z_i$ 들로 나뉘어진다는 것이다. 그리고 $q({\bf Z})$ 을 다음과 같이 쓸 수 있다.

q({\bf Z}) = \prod_{i=1}^{M} q_i(Z_i)

위와 같은 분포를 factorized distribution 이라고 한다.

위의 가정으로 $\mathcal{L}(q)$ 는 다음과 같이 쓸 수 있다. 표기법의 편의를 위해 $q_i = q_i(Z_i)$ 로 놓자.

\begin{aligned} \mathcal{L}(q) &= \int \prod_{i=1}^{M} q_i\Big( \log p({\bf X}, {\bf Z}) - \sum_{i=1}^M \log q_i \Big) \text{d}{\bf Z} \\ &= \int q_i \Big( \int \log p({\bf X}, {\bf Z}) \prod_{i\neq j}q_j \text{d}Z_{-i} \Big)\text{d}Z_i - \int q_i \log q_i \text{d}Z_i + const \\ & = \int q_i \log \tilde{p}({\bf X}, {Z_j}) \text{d}Z_i- \int q_i \log q_i \text{d}Z_i + const , \end{aligned}

여기서 $\log \tilde{p}({\bf X}, {Z_j}) = \mathbb{E}_{i\neq j}[\log p({\bf X}, {\bf Z})] + const$ 이며 역시 분포이다.

위의 마지막 식은 $q_j$ 와 $\tilde{p}({\bf X}, {Z_j})$ 의 negative KL-divergence임을 알 수 있다. 따라서 위의 ELBO를 최대화하는 것은 KL-divergence를 최소화하는 것이다. 두 분포가 동일하면 KL-divergence가 최소일 것이므로 $q_j = \tilde{p}({\bf X}, {Z_j})$ 일 때, 최소가 된다.

q^{\star}_i = \tilde{p}({\bf X}, {Z_j})

Properties of Factorized Approximations

Variational inference는 위에서 설명한 factorized approximation을 기반인데 이 방법도 문제가 있다. 그 문제를 이제 예를 통해서 확인해보자. 만약 실제 문제에서는 우리가 알 수 없지만 실험에서 $p({\bf X}, {\bf Z})$ 를 알고 있다고 하자. 이 실험에서는 데이터 $\bf X$ 가 없으므로 그냥 $p({\bf Z})$ 라고 하겠다. $p({\bf Z}) = \mathcal{N}({\bf Z} ; {\bf \mu}, {\bf \Lambda}^{-1})$ 이고 ${\bf Z} = (z_1, z_2)$ 를 확률변수로 갖는 이변량 정규분포의 모수들은 각각 아래와 같다.

{\bf \mu} = \left( \begin{matrix} \mu_1 \\ \mu_2 \end{matrix} \right), {\bf \Lambda} = \left( \begin{matrix} \Lambda_{11} & \Lambda_{12} \\ \Lambda_{12} & \Lambda_{22} \\ \end{matrix} \right)

위에서 처럼 $q({\bf Z}) = q_1(z_1)q_2(z_2)$ 로 생각하자. 그러면 위의 $q^\star$ 를 통해 업데이트 할 수 있는데

\begin{aligned} \ln q^{\star}_1(z_1) &= \mathbb{E}_{q_2}[\ln p( {\bf Z})] + \text{const}\\ &= \mathbb{E}_{q_2}[-\frac{\Lambda_{11}}{2}(z_1 - \mu_1)^2 - \Lambda_{12}(z_1 - \mu_1)(z_2 - \mu_2)] + \text{const} \\ &= -\frac{\Lambda_{11}}{2}z_1^2 + (\mu_1\Lambda_{11} - \Lambda_{12}(\mathbb{E}_{q_2}(z_2) - \mu_2))z_1 + \text{const}. \end{aligned}

근데 $\mathbb{E}_{q_2}(z_2)$ 는 윗 절의 유도과정에서 확인할 수 있지만 $q_2$ 를 probability measure로 하는 기댓값이다. 위의 꼴을 보면 $q_1^{\star}(z_1)$ 역시 정규분포임을 알 수 있다.

q_1^{\star}(z_1) = \mathcal{N}(z_1;\mu_1 -\Lambda_{11}^{-1}\Lambda_{12}(\mathbb{E}_{q_2}(z_2) - \mu_2), \Lambda_{11}^{-1})

$q_2^\star$ 도 위와 같은 방식으로 똑같이 구할 수 있고 정규분포임을 알 수 있다. 서로의 기댓값이 관여하기 때문에 초기값을 설정하고 반복적으로 $q_1^\star$ 와 $q_2^\star$ 를 수렴할 때까지 구한다면 해를 찾을 수 있을 것이다.

Variational Inference Issue

하지만 위의 방식대로 진행할 경우, 분산이 under-estimated될 수 있다. 실제로 Bishop의 책에서 실험한 결과를 보여주겠다.

위의 그림에서 왼쪽은 $\text{KL}(q\|p)$ , 오른쪽은 $\text{KL}(p\|q)$ 를 최소화한 경우이며 초록색은 실제 $p(X)$ , 빨간색은 $q(X)$ 를 의미한다.

그 이유는 KL-divergence 식으로 생각해 볼 수 있다.

\text{KL}(q|p) = \mathbb{E}_{q}\left(log\frac{q(X)}{p(X)}\right)

위의 KL-divergence를 줄이기 위해서는 $p(X)$ 가 $q(X)$ 를 dominate하는 분포여야한다. KL-divergence가 bounded되지 않는다. 즉, $q(X) > 0$ 이면 $p(X)>0$ 이다. 따라서 $p(X)$ 의 서포트가 더 넓어야하며 $q(X)$ 는 그보다는 작지만 KL-divergence를 줄이는 분포로 최적화된다.

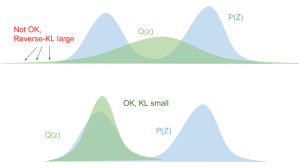
아래의 그림을 통해 더 쉽게 이해할 수 있다. 출처는 "Eric Jang"의 블로그이다.

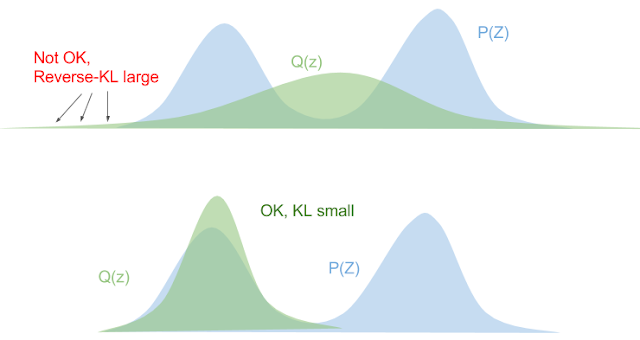그림 출처: "Eric Jang"의 블로그

위의 그림에서 2번째 그림을 보면 KL-divergence가 확 줄어들 것이다. $p(X)$ 는 쌍봉이지만 우리가 구한 최적의 $q(X)$ 는 단봉이다. 이러한 현상도 식을 통해 알 수 있는데 $p(X)$ 가 어떤 값을 가지던 $q(X) \rightarrow 0$ 이면 $log\frac{q(X)}{p(X)}$ 값은 작아지게 되고 KL-divergence도 매우 작아지게 된다. 따라서 위의 현상과 같이 분산이 under-estimated된다.

Variational inference에서의 위와 같은 문제를 해결하는 것이 큰 숙제가 아닐까 싶다. 그리고 KL-divergence를 계산하는 것도 실제 문제에서는 쉽지가 않다. 추후에 기회가 된다면 이러한 이슈들을 해결하기 위한 방법들에 대해서 공부해보고 포스팅해보겠다

chchch

머신러닝과 통계학을 공부하는 사람

다음 포스트

Variational Inference(변분 추론)

ML

Variational Inference

Factorized Distributions

Properties of Factorized Approximations

Variational Inference Issue

고차원 데이터와 차원의 저주(High-dimensional data and curse of dimensionality)

0개의 댓글