[C++] 백준 2485. 가로수

문제

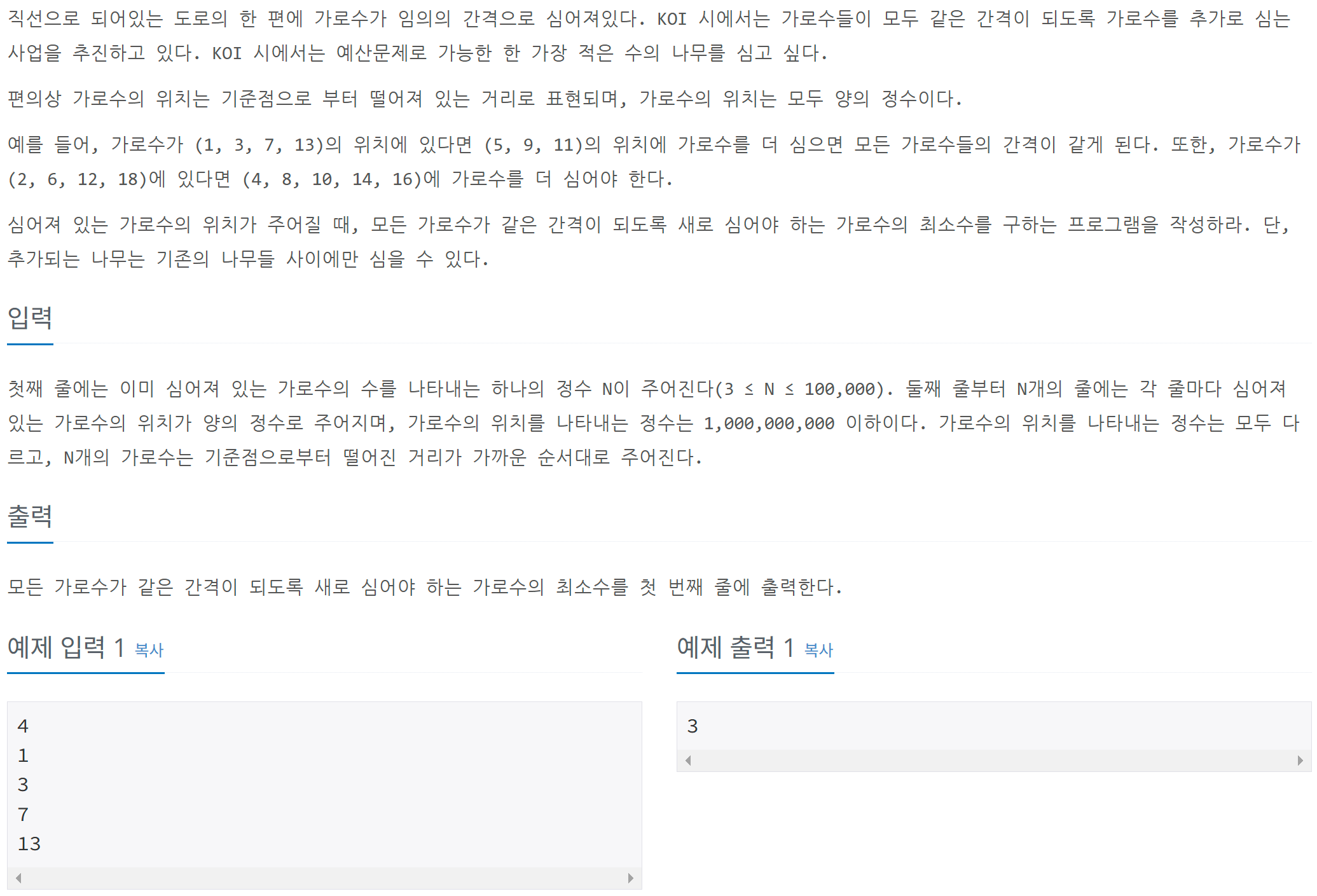
N개의 가로수들의 위치가 주어질 때, 가로수를 얼마나 더 심어야 모든 가로수 사이의 간격이 같아지는 지 출력하는 문제이다.
예산이 부족해서 가로수를 최소한으로 심어야 하는 게 킬포;

풀이

먼저 가로수 간 간격들의 최대공약수를 구한다.
그 다음, 첫 번째 가로수와 마지막 가로수 사이의 거리를
앞서 구한 최대공약수, 즉 최대의 동일한 간격으로 나눈다.

이 값은 최대 동일 간격으로 나무를 심을 때 필요한 나무 수이므로
이미 심겨져 있는 나무 수를 빼어 답을 구할 수 있다.

가로수 간 간격에 중복값은 필요가 없으므로 set에 넣어주고,
set을 반복자를 통해 돌면서 gcd 값의 최솟값을 구한다.

*, next

첫 관문은 set의 첫 번째 요소를 구하고자 하는 최대공약수에 넣어주는 거였는데 자꾸 int에 할당이 안된다고 하는거다.
뭔가 있었던 것 같은데 하면서 &를 붙였다가 *를 붙였더니 해결됐다.

그 다음 관문은 앞에서 두 번째 iterator부터 for문을 돌게 하고 싶은데
*i + 1로 넣어줬더니 그냥 요소 값에 1 더한 값이 나오는 거였다.
찾아보니 next 라는 게 있었다.
set은 vector나 array같은 순차 컨테이너가 아니라서,
*i + 1은 안된다 그러고 next를 썼더니 해결됐다.

코드

#include <iostream>
#include <algorithm>
#include <vector>
#include <unordered_set>
using namespace std;

int gcd(int a, int b) {
	if (b == 0) return a;
	else return gcd(b, a % b);
}

int main() {
	int n, t;
	cin >> n;

	vector<int> trees(n);
	for (int i = 0; i < n; i++) {
		cin >> trees[i];
	}

	unordered_set<int> s;
	for (int i = 0; i < n - 1; i++) {
		s.insert(trees[i + 1] - trees[i]);
	}

	int g = *s.begin();
	for (auto i = next(s.begin()); i != s.end(); i++) {
		g = gcd(g, *i);
		if (g == 1) break;
	}

	int ans = ((trees[n - 1] - trees[0]) / g) + 1 - n;
	cout << ans;

	return 0;
}

채점

나무 수만 알면 되니까 정렬 안하는 unordered 쓰면 더 좋아지나? 했는데
오잉 더 오래 걸리는 것

혼자 생각해보기론 정렬을 해두면 gcd 구할 때
두 값의 간격이 비교적 좁으니까 더 빨리 끝날 수도 있겠다 싶었다.