우리는 컴퓨터를 공부하며 많은 지식을 쌓는다. 그 중에는 지금 다루는 자료구조 파트도 있을 것이며, 컴퓨터 구조 파트도 있을 것이고, 운영체제 뭐.. 기타 등등 여러 분야를 공부할 것이다. 하지만 이런 것들을 공부하는 이유는 예전이나 지금이나 다를 바가 없을 것이다. 더욱 효율적이고, 더욱 빠르고, 더욱 정확하게 문제를 해결하려는 의도일 것이다. 이 처럼 문제를 해결하는 과정을 바로 Algorithm이라고 한다.

1. 알고리즘이란 이름의 유래

알고리즘이란 페르시아의 수학자 알-콰리즈미에서 유래되었다. 사담으로 영어로 대수학을 뜻하는 Algebra 또한 여기서 유래하였다.

2. 알고리즘은 무엇인가

알고리즘은 상술한 문제를 해결하는 과정을 뜻한다. 가령 예를 들자면

라면을 끓이고 싶다.(가독성을 위해 여러 과정을 스킵하였습니다.)

냄비를 갖고 온다.

물을 냄비에 담는다.

물이 끓었는가?

물에 스프를 넣고, 면을 넣는다.

...

위와 같이 문제에 대한 단계별 지시사항들을 CS(Computer Science)를 연구하는 사람들은 알고리즘(Algorithm)이라고 한다.

3. 알고리즘을 왜 분석하는가?

1. 알고리즘을 왜 연구하는가?

위에선 알고리즘에 대해서 다뤄보았고 이제부터는 어째서 알고리즘을 왜 연구하는가? 라는 것에 대한 내용이다.

만약 우리가 집에서 학교를 가야한다고 생각해보자. 그렇다면 우리는 집에서 학교를 어떻게 가야하는지를 생각해야 한다. 그렇다면 우리는 문 앞을 나서자마자 난관에 봉착한다. 왼쪽으로 가야하는지 오른쪽으로 가야하는지 직진으로 가야하는지, 계단을 이용해야하는지 엘리베이터를 이용해야하는지 등.
이러한 경우 알고리즘을 이용해 볼 수 있다.

학교를 갈 때 최대한 덜 걷고 가고 싶은지, 최대한 빨리 도착하고 싶은지, 가는 비용을 최소화하고 싶은지..

이러한 경우가 알고리즘을 필요로하는 경우라고 할 수 있다.
그렇다면 이러한 정보들, 즉 자료들을 중구난방으로 둔 상태로 사용자에게 보여주기엔 하나하나 찾아야 하기에 너무나도 느리거나, 부정확한 정보를 제공하게 된다. 그래서 이 자료들을 어떠한 형식에 따라 두기도 한다.

Example
정렬 알고리즘(퀵 정렬, 힙 정렬, 버블 정렬, 선택 정렬)
미로탐색 알고리즘(A* 알고리즘, 우선법, 좌선법 알고리즘, 다익스트라 알고리즘)
소수 찾기 알고리즘(에라토스테네스의 체)
등등

이 알고리즘들 외에도 연구 중이거나 연구 되었거나 하는 알고리즘들은 굉장히 많다.
아무튼 알고리즘을 분석하는 이유는 문제를 해결할 때에 시간적, 공간적으로 최적화되게 해결하는 것을 말한다.
일반적으로 시간적, 공간적 최적화 둘 중의 중요도는 [시간 > 공간]이다.

2. 알고리즘 분석의 목적

위에선 알고리즘을 연구하는 목적에 대해 다뤘고 후술할 내용은 알고리즘 분석의 목적이다.

알고리즘 분석의 목적은 비교를 하는 것인데. 상술했듯 일반적인 경우에는 코드의 수행시간이 얼마나 걸리는가가 우선 순위겠지만, 이 외에도 다른 이유들이 있다. 예를 들어, 수행 시간이 줄어드는 것에 비해 코드가 너무 길어져 가독성이 떨어진다거나, 개발자의 수고, 공간적인 한계로 인한 경우도 있을 것이다.

그렇다면 알고리즘을 분석한 것을 어떻게 비교할 것이냐. 라는 것의 문제이다.

1. 실행 시간 : 실행 시간은 위에서 얘기했듯 일반적으로 공간보다 시간을 더 중요하게 본다. 그렇다고 알고리즘 분석을 할 때의 척도로 내세우기엔 완벽하지 않은 부분도 있다. 일단 코드가 너무 길 수도 있고, 메모리를 너무 많이 잡아 먹을 수도 있다. 또한 시간을 척도로 보는데 해당 프로그램말고 다른 것이 실행되어있거나, 컴퓨터 주변환경이 너무 더워 CPU가 제 성능을 발휘하지 못할 수도 있다.

2. 구문의 수 : 컴파일러에게 명령을 하는 구문의 수를 갖고 비교하는 것은 좋은 해법이 아니다. 왜냐면 프로그래밍 언어에 따라 필요한 명령의 수가 천차만별이기 때문이다. 예를 들어 파이썬과 어셈블리어를 비교한다고 치면 모든 것을 일일이 정해줘야하는 어셈블리어와 비교적 느슨하게 코드를 작성해도 제기능을 하는 파이썬과는 큰 차이점이 있을 것이다.

   그렇다면 어떤 것이 좋은 알고리즘의 척도가 될 수 있을까?
   좋은 알고리즘의 척도를 f(n) 함수로 비교를 하는 것이다. 그리고 이 함수의 크기의 대소를 상대적으로 따져본다면 프로그램의 실행 시간, 언어에 따라 나뉘는게 아닌 좀 더 명확한 기준이 될 수 있을 것이다. 함수 f(n) 자체가 프로그램의 수행 시간을 나타내는 것이다.
   즉, 환경에 구애받지 않고 수행 시간을 나타낼 수 있는 f(n)을 사용하는 것이다.

1. 증가율은 무엇인가?

f(n) 함수의 입력 값(n)의 증가함에 따라 수행 시간이 증가하는 비율을 증가율이라고 한다.

예를 들어 백화점에 갔다고 가정하고
명품 매장에서 양말 한 켤레와 신발 한 켤레를 산다고 하면 신발이 200만원이고, 양말이 10만원일 때
총 비용 = 신발(200만원)+양말(10만원)이겠지만, 우리는 여기서 상대적으로 덜 중요한 양말의 값을 무시하기로 하는 것이다.
즉, 총 비용은 신발(200만원)이 되는 것이다.
만약 어떤 알고리즘의 수행시간이 n²+2n이라고 한다면 2n을 무시하고 가장 큰 차수를 가진 n²만 증가율에 포함한다는 것이다.

주로 쓰이는 알고리즘의 증가율은 1(Constant), logn(Logarithmic), n(Linear), nlogn(Linear Logarithmic),
n²(Quadratic), n³(Cubic), 2ⁿ(exponential), n!(Factorial) 등이 있다.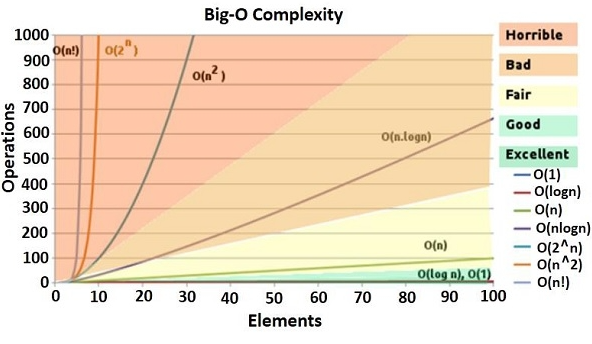

출처 : 구글 검색(점근 표기법)

이 외에도 굉장히 많은 증가율이 있지만 그건 알고리즘 파트에서 다루도록 하겠다.

2. 분석의 종류

분석의 종류에는 여러가지가 있다. 입력 값들에 따라서 알고리즘의 수행 속도가 달라질 수 있다.

예시로 수행 시간을 측정했는데 입력이 아주 운이 좋게 아무런 작업도 하지 않고 수행을 끝낼 수 있게 되는 최선의 경우(Best Case) vs 입력이 아주 나쁘게 들어와 한 번의 작업도 건너뛰지 말아야하는 최악의 경우(Worst Case) vs 입력이 무작위로 들어와 평균적으로 수행을 마치는 평균의 경우(Avarage Case) 등이 있을 수 있다.

최악의 경우 : f(n) = n²+2n+100
최선의 경우 : f(n) = 2nlogn
평균의 경우 : f(n) = 2nlogn+100

Big-O 표기법은 함수에 대해 상한을 찾게 해준다. 예시로, 위 수식들을 그래프로 그릴 때 n²의 상승폭이 밑의 logn의 상승폭보다 크니 다른 항들은 다 떼고 보고 그래프를 그린다는 것이다. 또한 일반적으로 f(n) = O(g(n))으로 표현된다. n의 값이 클 때(0 이상 일 때) f(n)의 상한이 g(n)의 상수배라는 말이다. 즉, 위에 함수로 예를 들면 f(n) = n²+2n+100이 주어진 알고리즘의 수행 시간이라면 g(n) = n²이라는 것이며, f(n)이 g(n)보다 크니 g(n)의 상수배가 f(n)의 상한이라는 것이다.

Big-O 표기법의 정의
O(g(n)) = {f(n): n ≥ n(0)인 경우인 모든 n에 대해 0 ≤ f(n) ≤ cg(n)을 만족하는 양의 상수 c와 n(0)이 존재한다.}
n이 작을 때에는 생략한다. 즉, n이 작을 경우의 상승폭은 중요치 않다라는 얘기다.

즉, Big-O Notation에 의하면 상술한 O(n²)가 O(n³), O(n⁴)도 된다는 것이다.

Omega 표기법은 함수의 하한을 찾게 해준다. 이 것은 n의 값이 클 때에 f(n)의 하한이 g(n)의 상수배라는 것이다. 예시로, 위에 작성한 함수를 이용해보자면 f(n) = n²+2n+100일 때에 Ω(n²)라는 것이다.

Omega 표기법의 정의
O(g(n)) = {f(n): n ≥ n(0)인 경우인 모든 n에 대해 0 ≤ cg(n) ≤ f(n)을 만족하는 양의 상수 c와 n(0)이 존재한다.} 예를 들어, f(n) = 1/2*n²인 경우에 이 함수의 하한은 n², n, logn.. 그 외 등등이 있을거다.

또한 Big-O 표기법은 연산 수에 큰 영향을 주지 않는 가지들을 모두 쳐내고 표기한다. 상수를 나타내는 1은 10억이 되어도 1이고 한 번만 실행되어도 1이다. n또한 2n도 n이고 100n도 n으로 나타내듯 시각화할 수 있다.

Tight 표기법은 알고리즘의 평균 수행 시간은 항상 하한과 상한 사이에 존재한다. 만약 상한(O)과 하한(Ω)이 같다면 세타(θ) 표기법 또한 같은 증가율을 같는다.

예를 들어 f(n) = 10n²+n의 상한은 O(n²)이 되고, 하한도 Ω(n²)가 된다. 이 경우 최선의 경우와 최악의 경우의 증가율이 같다. 결과적으로 Tight-Bound의 경우 또한 같아진다.

Tight 표기법의 정의
O(g(n)) = {f(n): n ≥ n(0)인 경우인 모든 n에 대해 0 ≤ c₁g(n) ≤ f(n) ≤ c₂g(n)을 만족하는 양의 상수 c₁과 c₂와 n(0)이 존재한다.}

이해가 되지 않는 사람들을 위해 덧붙이자면, g(n)이 n일 경우 c의 하한은 만족할지라도 상수배로 증가하는 n에 c를 아무리 곱한다 한들 제곱수만큼 증가하는 n²보다 항상 클 수가 없다는 것이다. n²의 경우에서도 n의 상한은 만족할지라도 하한은 만족하지 못할 것이다.

하지만 현재 컴퓨터를 공부하는 90% 이상의 사람들은 세타의 의미로 Big-O 표기법을 사용하고 있으며 세타 표기법을 사용하는 사람들은 드물다.

4. 점근적 분석인 이유

f(n)에 대하여 n의 값이 클 경우 f(n)에 근접한 다른 함수 g(n)을 찾으려 한다.
이 말은 g(n)은 n이 큰 경우 f(n)에 근접한 곡선이라는 뜻이다.
수학에선 이러한 말을 점근선(Asymptote)이라고 한다. 이러한 성질로 인해 점근적 분석(Asymptotic Analysis)이라고 하는 것이다.

5. 점근적 분석을 구하는 법

여태까지 구구절절히 이 알고리즘의 f(n)의 상한이 어떻고, 하한이 어떻고 상한과 상한의 사이에 있는 점근적 분석이 어떻고를 공부했다면 이제는 그래서 점근적 분석을 어떻게 구하는 것인가를 구해볼 것이다.

for (i = 1; i <= n; i++) {
	m = m + 2; //계산하는 시간 c
}

계산하는 상수 시간을 상수 c로 두고 입력 값인 n만큼 loop를 돌리는 코드이니

전체시간 = 상수(c)*입력 값(n) = cn 이나, 계수를 뺴고 봐야 한다.

즉, O(n)이 되는 것이다

for (i = 1; i <= n; i++) {
	for (j = 1; j <= n; j++) {
    	k = k + 1; //계산하는 시간 c
	}
}

위의 loop를 2중으로 바꾼 코드이다. 그렇다면 초보 개발자들은 여기서 함정에 빠진다. loop가 두 개이니 이 코드의 수행 시간은 2n이겠구나하고 말이다. 하지만 이 코드는 i가 한 번 돌고 j가 n만큼 돌고 다시 i가 한 번 돌고 j가 n만큼 돌고 하는 코드이다. 즉,

전체시간 = 전체시간 = 상수(c)*입력 값(n)*입력 값(n) = cn²이다.

해당 2중 loop 코드는 O(n²)짜리 코드인 것이다.

x = x + 1; //일정한 시간 c(0)
for (i = 1; i <= n; i++) {
	y = y + 1; //일정한 시간 c(1)
	for (j = 1; j <= n; j++) {
    	k = k+1; //일정한 시간 c(2)
    }
}

위와 같은 코드도 같은 식으로 분석해주면 된다.

전체시간 = c(0)+n*(c(1)+n*c(2))이 되며, 계수를 빼고 보면

O(n²)이 되는 것이다.
2중 loop안에(또는 밖에) 얼마나 많은 연산을 하던 우리는 최고차항만 보면 된다.

이제껏 봐온 케이스들은 그저 loop만 돌면서 연산하고 그걸 분석하였다면 좀 더 상위 개념을 다룰 필요가 있다.

if (length() == 0) {
	return false; //then 부분: 상수 c(0)
} else { //(상수+상수)*n
	... //상수 c(1)
    for (int i = 0; i < length(); i++) {
    	... //또 다른 상수 c(2)
        if (!list[i].cquals(otherList.list[i])) {
       		//상수 c(3)
            return false;
        }
    }
}

해당 코드에서 최선의 경우는 입력의 크기가 0인 경우 바로 c(0)만큼의 연산으로 코드가 끝나버리는 것이고 그 외에는 c(1)+n*(c(2)+c(3))인 것이다. 구하는 법은 if의 경우 else의 경우 모두 더하고 분석하는 것이다.

전체시간 = c(0)+(c(1)n*(c(2)+c(3)))이다.

여기서 최고차항만 보고 계수를 버리면 O(n)이 되는 것이다.
이게 끝이다. 모든 코드에 이런 식으로 분석할 수 있다면 점근적 분석에 대해 모두 제대로 배웠다고 말할 수 있는 것이다.
이 쯤에서 궁금할 것이다. 알고리즘을 짜면서 loop와 sequence와 if-then-else밖에 없느냐? 이거 밖에 없다. 아무리 날고 기는 코드를 짜도 이 밖을 벗어날 수는 없다.

단, 한 가지 더 알아야 하는 코드의 유형이 있다.

for (i = 1; i <= n; ) {
	i = i * 2;
}

이런 유형의 코드이다. 반복을 할 때마다 남은 범위의 절반씩, 절반의 절반, 뭐 반의 반, 그 반의 반 이런 식으로 수행하는 코드를 보면 당황할 것이다. 그런 사람들을 위해 직접 보여주겠다.

n = 1000이라고 가정하고 i의 변화를 보면,
i = 1
i = 2
i = 4
i = 8
i = 16
i = 32
i = 64
i = 128
i = 256
i = 512
i = 1024
단 10번의 loop로 i를 1000 이상으로 증가를 시켰다.

이게 왜 log냐

log n = log a^b

직접 계산하여 보면 log 2^10 = 3.01···으로 나오게 된다.

예시로 이분 탐색(이진 탐색)을 예시로 들 수 있는데, 나보다 큰 수는 오른쪽, 나보다 작은 수는 왼쪽에 넣는다고 가정하면 아래와 같은 트리형 구조가 나온다.

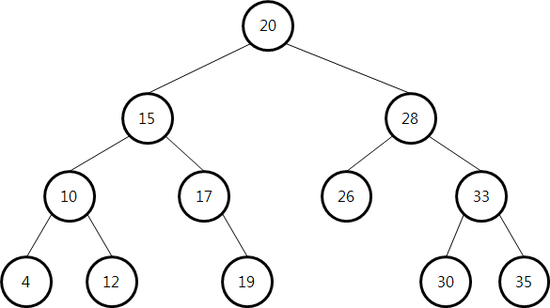
출처 : 구글 검색 (트리 구조)

만약 해당 트리에서 33에 해당하는 수를 찾고 싶다 하면 20을 기준으로 크니까 오른쪽, 28을 기준으로 크니까 다시 오른쪽으로 가면 단 두 번의 탐색으로 33이란 수를 찾을 수 있게 되는 것이다. 그리고 왼쪽으로 가던, 오른쪽으로 가던 어떤 선택을 하던 간에 찾아야 할 범위가 1/2씩 줄어드니 이분 탐색이 대표적인 O(logn)의 수행 시간을 갖는다는 예시로 뽑힌다.