8. 트리(Tree)

이 내용은 윤성우의 열혈 자료구조를 학습한 내용입니다.

1. 트리의 개요

1-1. 트리의 접근

트리는 계층적 관계(Hierarchical Reelationship)를 표현하는 자료구조다.

자료구조는 근본적으로 무엇인가를 ‘표현’하는 도구이다.

• 표현을 위해서는 저장과 삭제라는 기능이 제공되어야 한다.

1-2. 트리 관련 용어의 소개

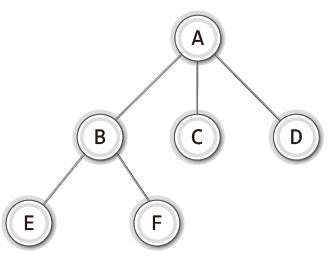
• 노드(node)
  • 트리의 구성요소에 해당하는 모든 요소
• 간선(edge)
  • 노드와 노드를 연결하는 연결선
• 루트 노드(root node)
  • 트리 구조에서 최상위에 존재하는 A 와 같은 노드
• 단말 노드(terminal node)/잎사귀 노드(leaf node)
  • 아래로 또 다른 노드가 연결되어 있지 않은 E, F, C, D 와 같은 노드
• 내부 노드(internal node)/비단말 노드(nonterminal node)
  • 단말 노드를 제외한 모든 노드로 A, B와 같은 노드

✔️ 노드의 관계

트리 구조상 위에 있을수록 촌수가 높다.

• 부모(parent)
  • 간선으로 연결된 노드 중 촌수가 높은 노드
• 자식(child)
  • 간선으로 연결된 노드 중 촌수가 낮은 노드
• 형제(sibling)
  • 부모가 같은 노드(촌수가 같다.)

• 조상(Ancestor)
  • 특정 노드 위에 위치한 모든 노드
• 후손(Descendant)
  • 특정 노드의 아래에 위치한 모든 노드

1-3. 이진 트리와 서브 트리

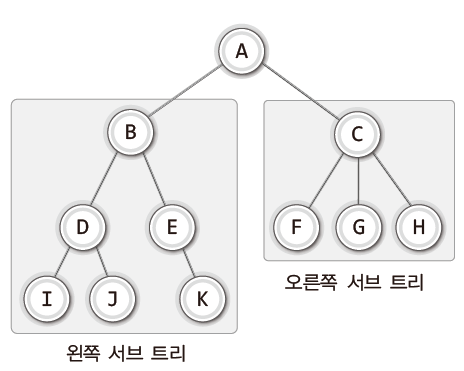
위 그림과 같이 큰 트리는 작은 트리로 구성이 된다.

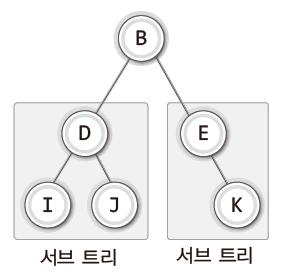
• 서브 트리(sub tree)
  • 큰 트리에 속하는 작은 트리
  • 서브 트리 역시 또 다른 서브 트리를 갖는다.
    → 트리 구조는 재귀적이다.
    

✔️ 이진 트리(binary tree)

• 이진 트리의 조건
  1. 루트 노드를 중심으로 두 개의 서브 트리로 나뉘어진다.
  2. 나뉘어진 두 서브 트리도 모두 이진 트리이어야 한다.
  • 노드가 위치할 수 있는 곳에 노드가 존재하지 않는다면, 공집합(empty set) 노드가 존재하는 것으로 간주한다. → 공집합 노드도 이진 트리의 판단에 있어서 노드로 인정한다.
    

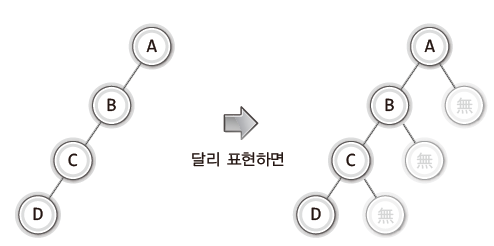
1-4. 포화 이진 트리와 완전 이진 트리

🔻 트리 관련 용어

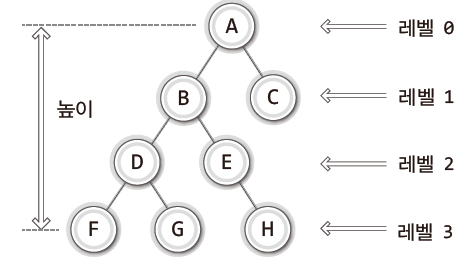
• 레벨(level): 트리의 각 층
• 높이(height): 트리의 최고 레벨

• 포화 이진 트리(full binary tree)
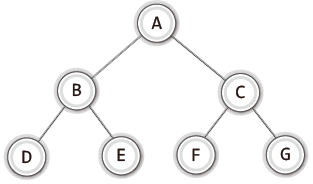
  • 모든 레벨이 꽉 찬 이진 트리

• 완전 이진 트리(complete binary tree)
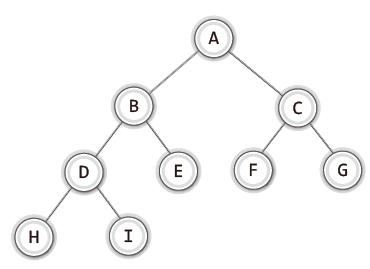
  • 모든 레벨이 꽉 찬 상태는 아니지만, 차곡차곡 빈 틈 없이 노드가 채워진 이진 트리
  • 위에서 아래로, 왼쪽에서 오른쪽으로 채워진 트리

2. 이진 트리의 구현

이진 트리는 재귀적인 특성을 지니고 있다. (서브트리의 서브트리)

2-1. 이진 트리의 구현 방법: 배열 기반 or 연결 리스트 기반

• 배열 기반
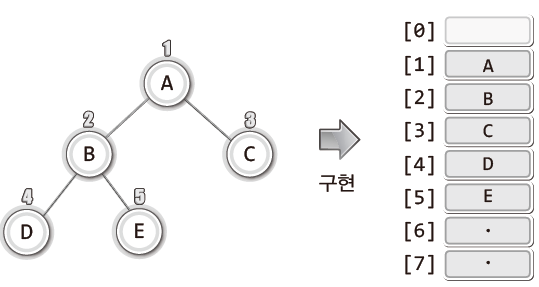
  • 연결 리스트에 비해 탐색이 용이하다.
  • 노드에 번호를 부여하고 그 번호에 해당하는 값을 배열의 인덱스 값으로 활용한다.
  • 편의상 배열의 첫 번째 요소는 사용하지 않는다.

• 연결 리스트 기반
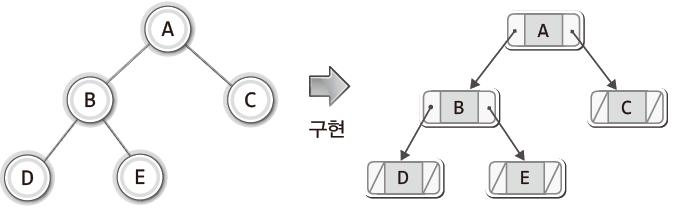
  • 트리의 구조와 리스트의 연결 구조가 일치한다.

2-2. 헤더파일에 정의된 구조체의 이해

#ifndef __BINARY_TREE_H__
#define __BINARY_TREE_H__

typedef int BTData;

typedef struct _bTreeNode // 이진 트리의 노드를 표현한 구조체
{
	BTData data;
	struct _bTreeNode * left;
	struct _bTreeNode * right;
} BTreeNode;

BTreeNode * MakeBTreeNode(void);
BTData GetData(BTreeNode * bt);
void SetData(BTreeNode * bt, BTData data);

BTreeNode * GetLeftSubTree(BTreeNode * bt);
BTreeNode * GetRightSubTree(BTreeNode * bt);

void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub);
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub);

#endif

• 하나의 노드는 그 자체로 이진트리이다.(두 개의 공집합 노드를 자식 노드로 두고 있다.) → 노드를 표현한 구조체는 실제로 이진 트리를 표현한 구조체가 된다.
  • 노드의 표현결과
  • 이진 트리의 표현결과

이진 트리의 모든 노드는 직/간접적으로 연결되어 있다.
따라서 루트 노드의 주소 값만 기억하면, 이진트리 전체를 가리키는것과 다름이 없다.

2-3. 헤더파일에 선언된 함수들의 기능

• 노드의 생성, 데이터의 반환 및 저장
  • BTreeNode * MakeBTreeNode(void);: 노드의 생성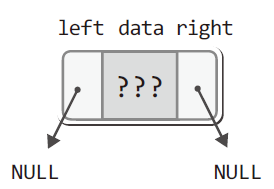
    • 노드를 동적 할당 및 초기화하여 그 주소 값을 반환한다.
    • 쓰레기 값으로 data가 저장된다.
    • 포인터 변수 left와 right는 NULL로 자동 초기화 된다.
  • BTData GetData(BTreeNode * bt);: 노드에 저장된 데이터를 반환
  • void SetData(BTreeNode * bt, BTData data);: 노드에 데이터를 저장

• 주소 값 반환
  • BTreeNode * GetLeftSubTree(BTreeNode * bt);: 왼쪽 서브 트리(노드) 주소 값 반환
  • BTreeNode * GetRightSubTree(BTreeNode * bt);: 오른쪽 서브 트리(노드) 주소 값 반환

• 서브 트리의 연결
  • 매개변수 sub 로 전달된 트리 또는 노드를 매개변수 main 으로 전달된 노드에 연결한다.
  • void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub);: 왼쪽 서브트리를 연결한다.
  • void MakeRightSubTree(BTreeNode * main, BTreeNode * sub);: 오른쪽 서브 트리를 연결한다.

2-4. 이진 트리의 구현

• 노드의 생성, 데이터의 반환 및 저장
  • BTreeNode * MakeBTreeNode(void);: 노드의 생성 후 그 주소 값을 반환

    BTreeNode * MakeBTreeNode(void)
    {
    	BTreeNode * nd = (BTreeNode*)malloc(sizeof(BTreeNode));
    
    	nd->left = NULL;
    	nd->right = NULL;
    	return nd;
    }

  • BTData GetData(BTreeNode * bt);: 노드에 저장된 데이터를 반환

    BTData GetData(BTreeNode * bt)
    {
    	return bt->data;
    }

  • void SetData(BTreeNode * bt, BTData data);: 노드에 데이터를 저장

    void SetData(BTreeNode * bt, BTData data)
    {
    	bt->data = data;
    }

• 주소 값 반환
  • BTreeNode * GetLeftSubTree(BTreeNode * bt);: 왼쪽 서브 트리(노드) 주소 값 반환

    BTreeNode * GetLeftSubTree(BTreeNode * bt)
    {
    	return bt->left;
    }

  • BTreeNode * GetRightSubTree(BTreeNode * bt);: 오른쪽 서브 트리(노드) 주소 값 반환

    BTreeNode * GetRightSubTree(BTreeNode * bt)
    {
    	return bt->right;
    }

• 서브 트리의 연결

  왼쪽 또는 오른쪽 서브 트리가 존재한다면, 해당 트리를 삭제하고서 새로운 왼쪽 또는 오른쪽 서브 트리를 연결한다.

  • void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub);: 왼쪽 서브트리 연결

    void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub)
    {
    	if(main->left != NULL)
    		free(main->left);
    
    	main->left = sub;
    }

  • void MakeRightSubTree(BTreeNode * main, BTreeNode * sub);: 오른쪽 서브 트리 연결

     void MakeRightSubTree(BTreeNode * main, BTreeNode * sub)
     {
     	if(main->right != NULL)
     		free(main->right);
     
     	main->right = sub;
     }

📌 문제 발생

• 둘 이상의 노드로 이뤄져 있는 서브 트리를 완전히 삭제하려면 서브 트리를 구성하는 모든 노드를 대상으로 free 함수를 호출해야 한다.
  → 모든 노드를 방문해야 한다. (순회: traversal)

• 이진 트리 생성(main)

  #include <stdio.h>
  #include "BinaryTree.h"
  
  int main(void)
  {
  	/*** 노드 생성 ***/
  	BTreeNode * bt1 = MakeBTreeNode();
  	BTreeNode * bt2 = MakeBTreeNode();
  	BTreeNode * bt3 = MakeBTreeNode();
  	BTreeNode * bt4 = MakeBTreeNode();
  
  	/*** 데이터 저장 ***/
  	SetData(bt1, 1);
  	SetData(bt2, 2);
  	SetData(bt3, 3);
  	SetData(bt4, 4);
  
  	/*** 연결 관계 생성 ***/
  	MakeLeftSubTree(bt1, bt2);
  	MakeRightSubTree(bt1, bt3);
  	MakeLeftSubTree(bt2, bt4);
  
  	printf("%d \n",
  		GetData(GetLeftSubTree(bt1))); // 2
  	printf("%d \n",
  		GetData(GetLeftSubTree(GetLeftSubTree(bt1)))); // 4
  
  	return 0;
  }

3. 이진 트리의 순회(Traversal)

3-1. 순회의 세 가지 방법

루트 노드를 언제 방문하는가에 따라 나뉜다.

• 전위 순회(Preorder Traversal): 루트 노드를 먼저

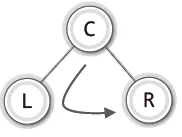
• 중위 순회(Inorder Traversal): 루트 노드를 중간에

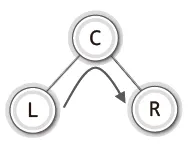
• 후위 순회(Postorder Traversal): 루트 노드를 마지막에

3-2. 순회의 재귀적 표현

• 재귀의 탈출 조건

  • 서브 트리가 NULL 인 경우 탈출한다.

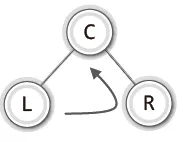
• 반복 패턴(중위 순회 기준)

  

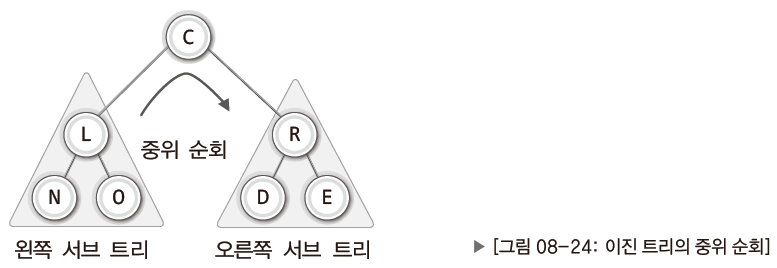
  1. 왼쪽 서브 트리의 순회
  2. 루트 노드의 방문
  3. 오른쪽 서브 트리의 순회

void InorderTraverse(BTreeNode * bt)
{
	if(bt == NULL)    // bt가 NULL이면 탈출한다. 
		return;

	InorderTraverse(bt->left); 
	printf("%d \n", bt->data); // 방문 시 다양한 함수 처리를 할 수 있다.
	InorderTraverse(bt->right); 
}

3-3. 이진트리의 완전 소멸

void DeleteTree(BTreeNode * bt)
{
	if(bt == NULL)
		return;

	DeleteTree(bt->left);
	DeleteTree(bt->right);
	free(bt); // 방문시 처리 함수
}

• 루트 노드가 마지막에 소멸되어야 하기 때문에 반드시 후위 순회 과정을 통해서 소멸을 진행해야 한다.

참고: 윤성우의 열혈 자료구조