오늘의 회고

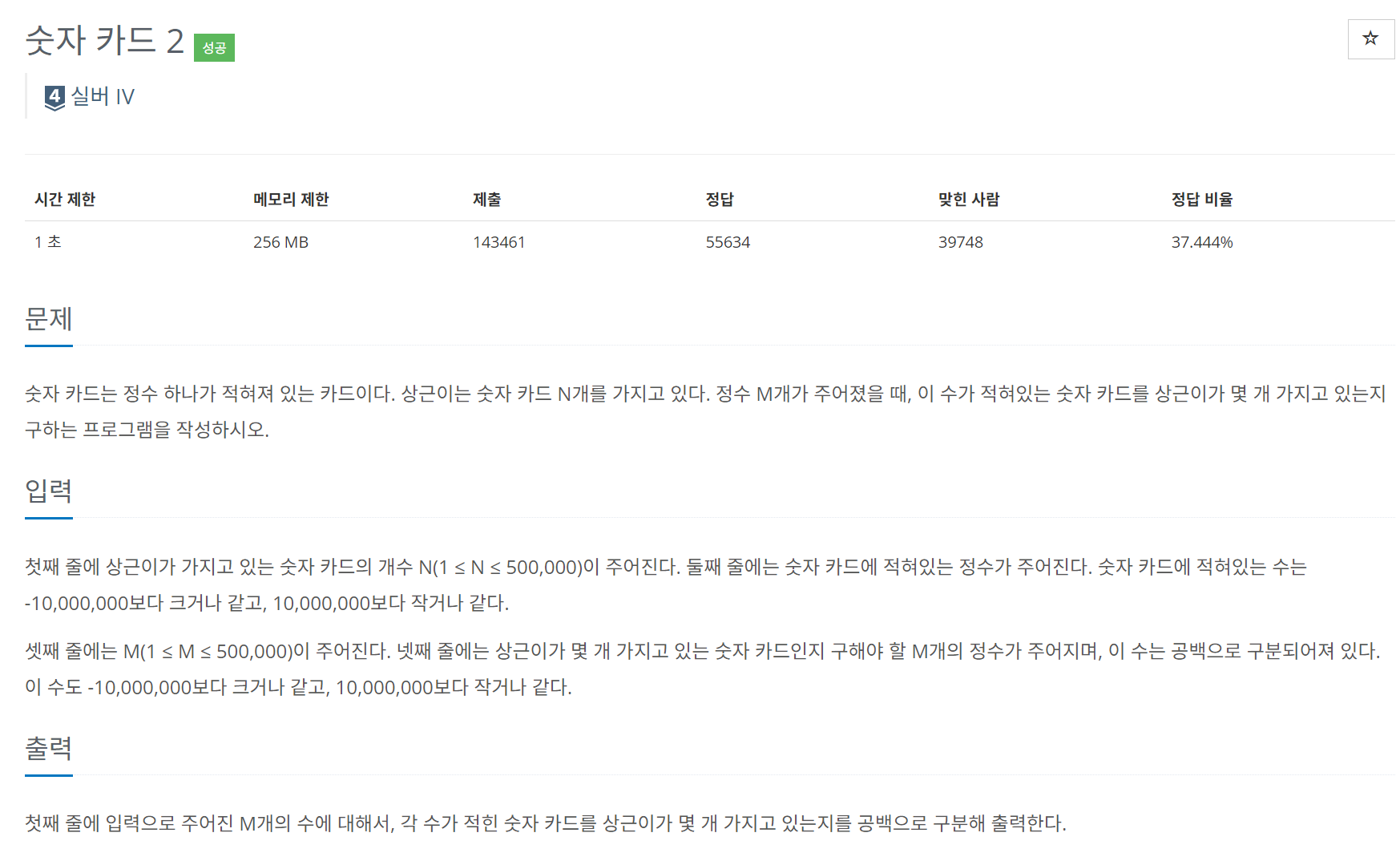
오랜만에 이분탐색을 복습할 겸 관련 문제를 백준 10816번 숫자 카드 2 풀었다.

시도한 것

for x in M_list:
    low = 0
    high = N-1
    cnt = 0
    while low <= high:
        mid = (low + high) // 2
        if x < N_list[mid]:
            high = mid - 1
        elif x > N_list[mid]:
            low = mid + 1
        else:
            cnt += 1
        
    print(cnt, end=' ')

만약 찾으려는 숫자가 mid 값보다 작으면 high 인덱스를 감소시키고
mid 값보다 크면 low 인덱스를 증가시키고 같으면 cnt를 1 증가 시키는 방식으로 짰다.
중복되는 숫자가 없었다면 이런 식으로 풀면 됐을 것이다. 하지만 이 문제는 리스트에 중복되는 숫자도 허용하기 때문에 이렇게 하게 되면 종료조건이 애매하게 된다.

만약 target이 9이고 리스트에서 9를 찾았을 때 찾은 9는 여러 중복되는 숫자 중에서 마지막에 있는지, 중간에 있는지, 처음에 있는지 모르니까 high 인덱스를 감소시켜야할지, low 인덱스를 증가시켜야할지 막막했다.

해결방법

target이 리스트에 오름차순 정렬을 해치지 않는다고 가정할 때,
마지막에 들어갈 수 있는 위치와 처음 들어갈 수 있는 위치의 차를 구하면 된다.

리스트는 [2, 5, 6, 9, 9, 9, 11, 13]
ex1) 이 리스트에서 target이 9일 때
9가 마지막으로 들어갈 수 있는 인덱스는 6, 처음 들어갈 수 있는 인덱스는 3
이 둘의 차는 3 즉, 9는 3번 나온다.

ex2) 같은 리스트에서 target이 6일 때
6이 마지막으로 들어갈 수 있는 인덱스는 3, 처음 들어갈 수 있는 인덱스는 2
이 둘의 차는 1 즉, 6은 1번 나온다.

ex3) 같은 리스트에서 target이 10일 때
10이 마지막으로 들어갈 수 있는 인덱스는 6, 처음 들어갈 수 있는 인덱스는 6
이 둘의 차는 0 즉, 10은 0번 나온다.

---

처음 들어갈 수 있는 인덱스는 lower_idx 함수
마지막에 들어갈 수 있는 인덱스는 upper_idx 함수
이 함수들의 차이는 딱 하나이다.

N_list[mid] == target일 때
high = mid => lower_idx 함수 (이렇게 해야 왼쪽 부분 탐색)
low = mid + 1 => upper_idx 함수 (이렇게 해야 오른쪽 부분 탐색)

정답 코드

import sys
input = sys.stdin.readline

N = int(input())
N_list = list(map(int, input().split()))
M = int(input())
M_list = list(map(int, input().split()))

N_list.sort()

def lower_idx(target):
    high = N
    low = 0
    while low < high:
        mid = (low + high) // 2
        if target <= N_list[mid]:
            high = mid
        else:
            low = mid + 1
    return low

def upper_idx(target):
    high = N
    low = 0
    while low < high:
        mid = (low + high) // 2
        if target < N_list[mid]:
            high = mid
        else:
            low = mid + 1
    return low

for x in M_list:
    result = upper_idx(x) - lower_idx(x)
    print(result, end=' ')