4. Greedy Algorithm(2)

4.3 Shortest Path

• 주어진 가중치 그래프에서 어느 한 출발점에서 또 다른 도착점까지의 최단 경로를 찾는 문제
• Dijkstra Algorithm
  • 최단 경로를 찾는 가장 대표적인 알고리즘
  • 최단 거리가 확정되지 않은 정점들 중 출발점에서 가장 가까운 점을 선택해 최단 거리로 확정

ShortestPath(G,s)

• Input: 가중치 그래프 $G=(V,E), |V|=n, |E|=m$
• Output: 출발점 $s$로부터 n-1개의 점까지각각 최단 거리를 저장한 배열 $D$

1. $D$를 $\infin$로 초기화. 단, $D[s]=0$으로 초기화
2. while (s로부터의 최단 거리가 확정되지 않은 점이 있으면)
3. 현재까지 최단 거리가 확정되지 않은 점 $v$에 대해서 최소의 $D[v]$의 값을 가진 점 $v_{min}$을 선택하고, $s$로부터 점 $v_{min}$까지의 최단 거리 $D[v_{min}]$ 확정
4. $s$로부터 현재보다 짧은 거리로 점 $v_{min}$을 통해 우회 가능한 점 $w$에 대해서 $D[w]$를 갱신 // 간선 완화
5. return $D$

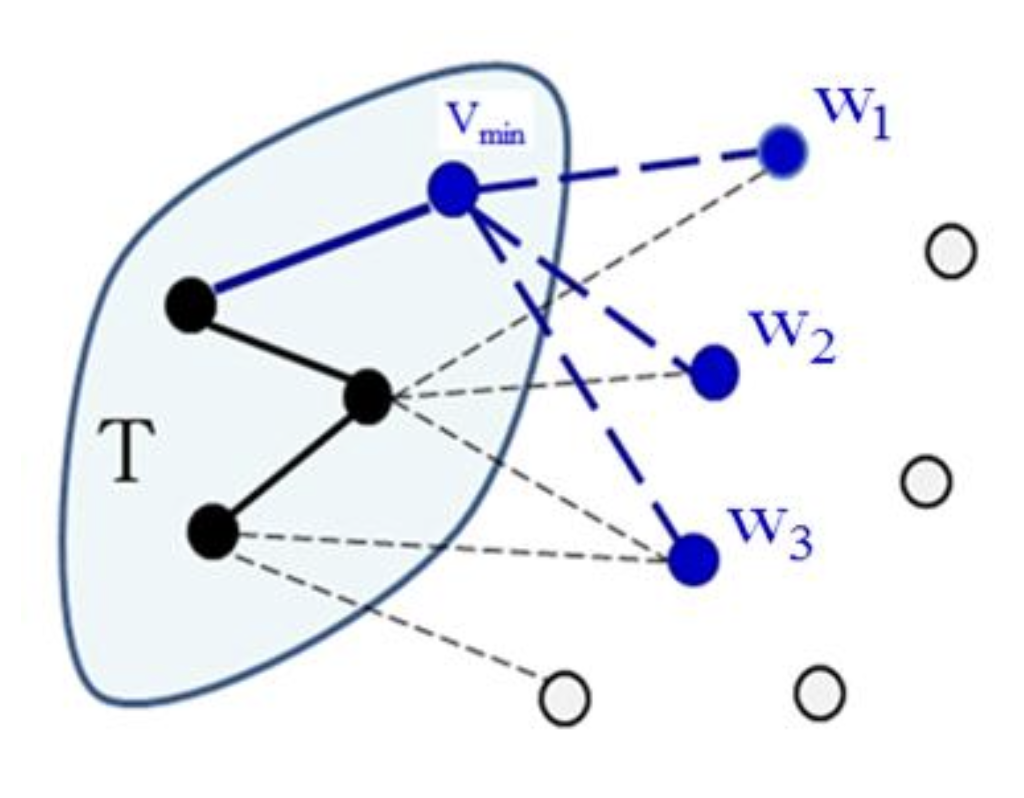
4.3.1 Edge Relaxation

Line4

• 최단 거리가 확정된 정점 $v_{min}$의 이웃 정점 $w$에 대해,
• 출발점에서 $v_{min}$까지의 최단 거리와, $v_{min}$에서 $w$로 가는 간선의 가중치의 합이 현재 저장된 $D[w]$ 값보다 작다면, $D[w]$ 값을 더 작은 값으로 갱신

4.3.2 Procedure

1. 시작점 - 서울 확정

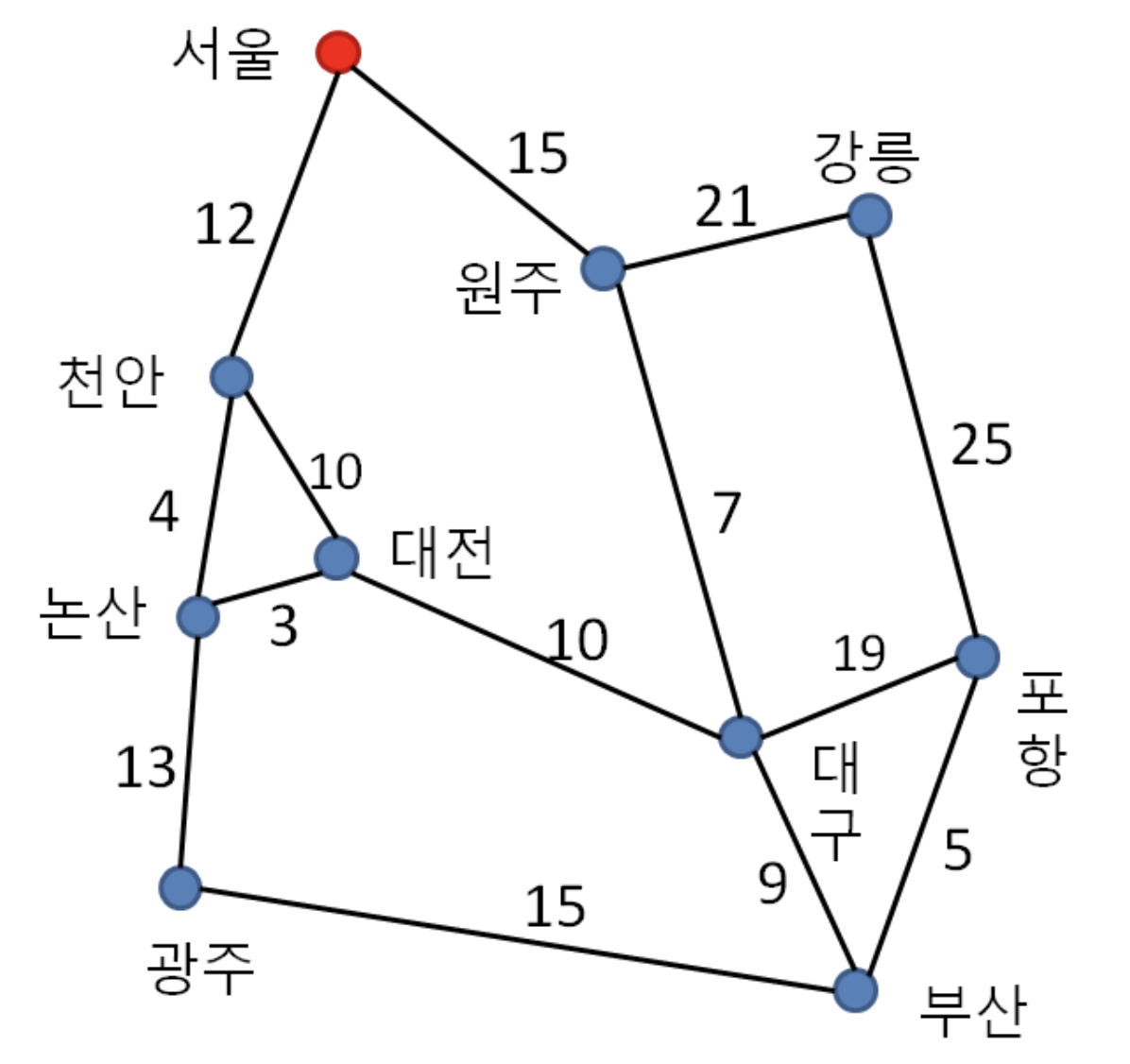
2. 간선 완화

• 현재 최솟값 정점에서 직접 연결된 이웃 정점 $w$로 가는 경로의 거리 갱신
  

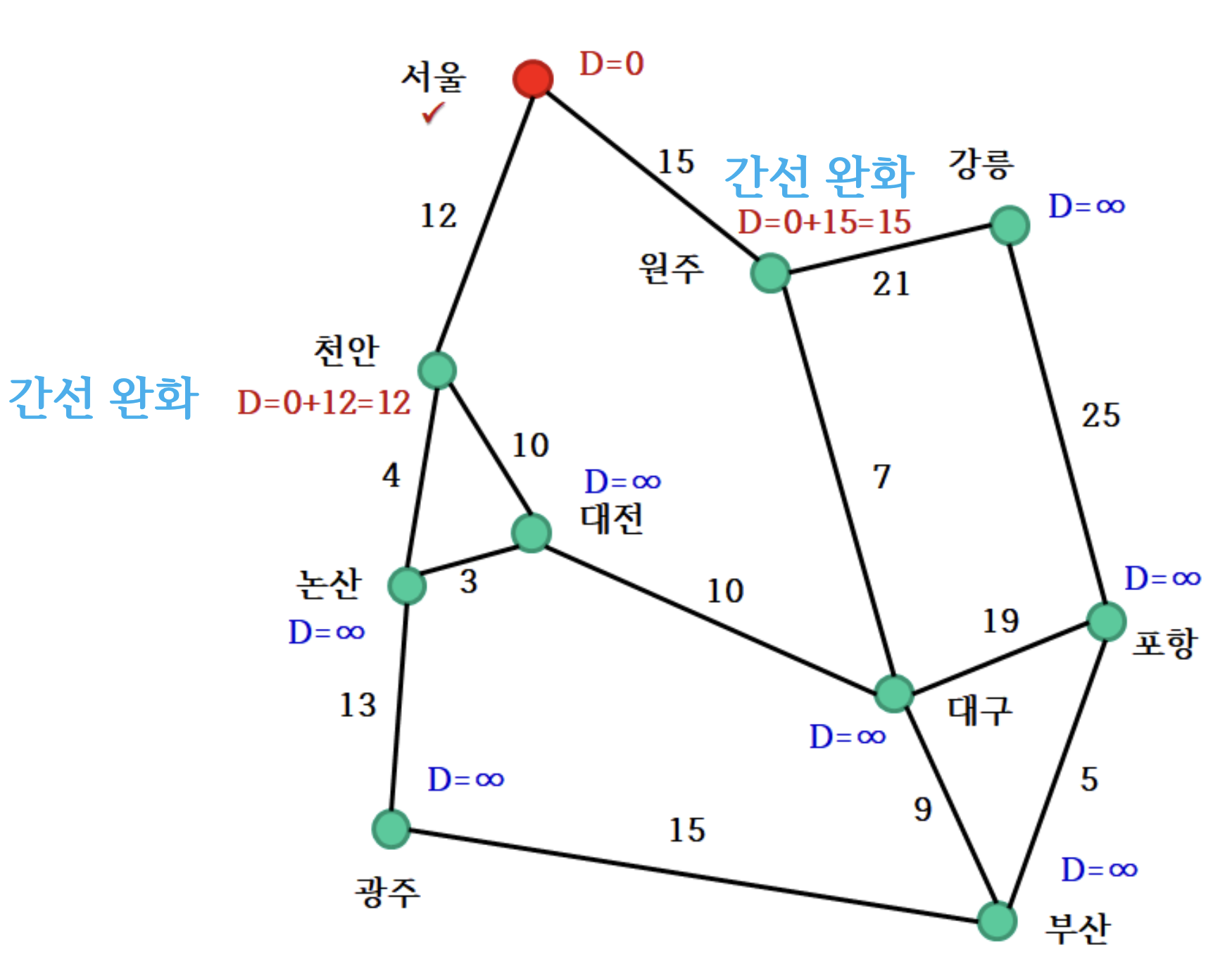
3. 천안 확정

• 다음에 최단 거리를 확정할 점은 적어도 한 번은 간선 완화 과정을 거쳐서 기존 무한대였던 거리가 갱신된 점이어야 후보가 된다.
  

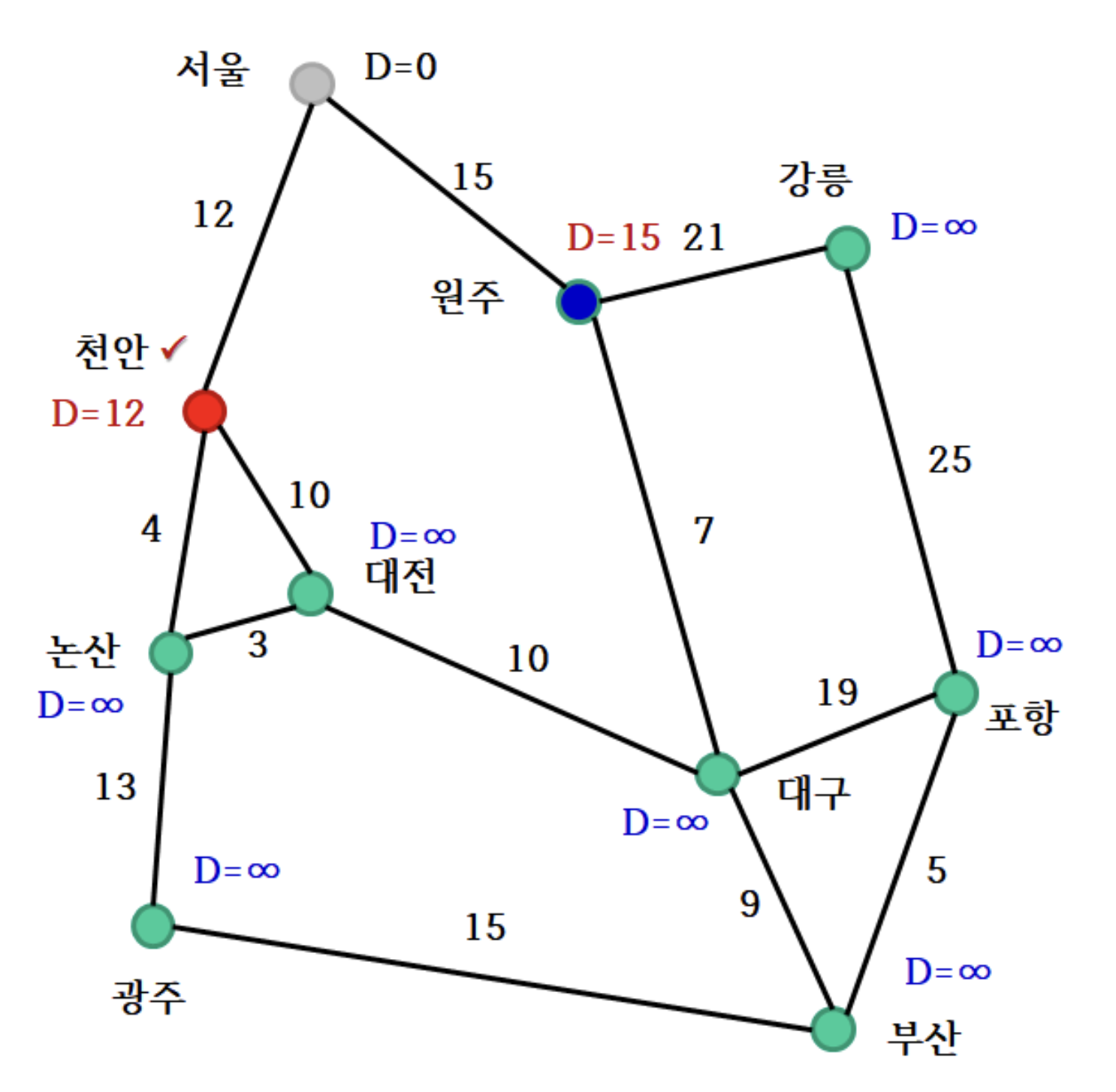
4. 간선 완화

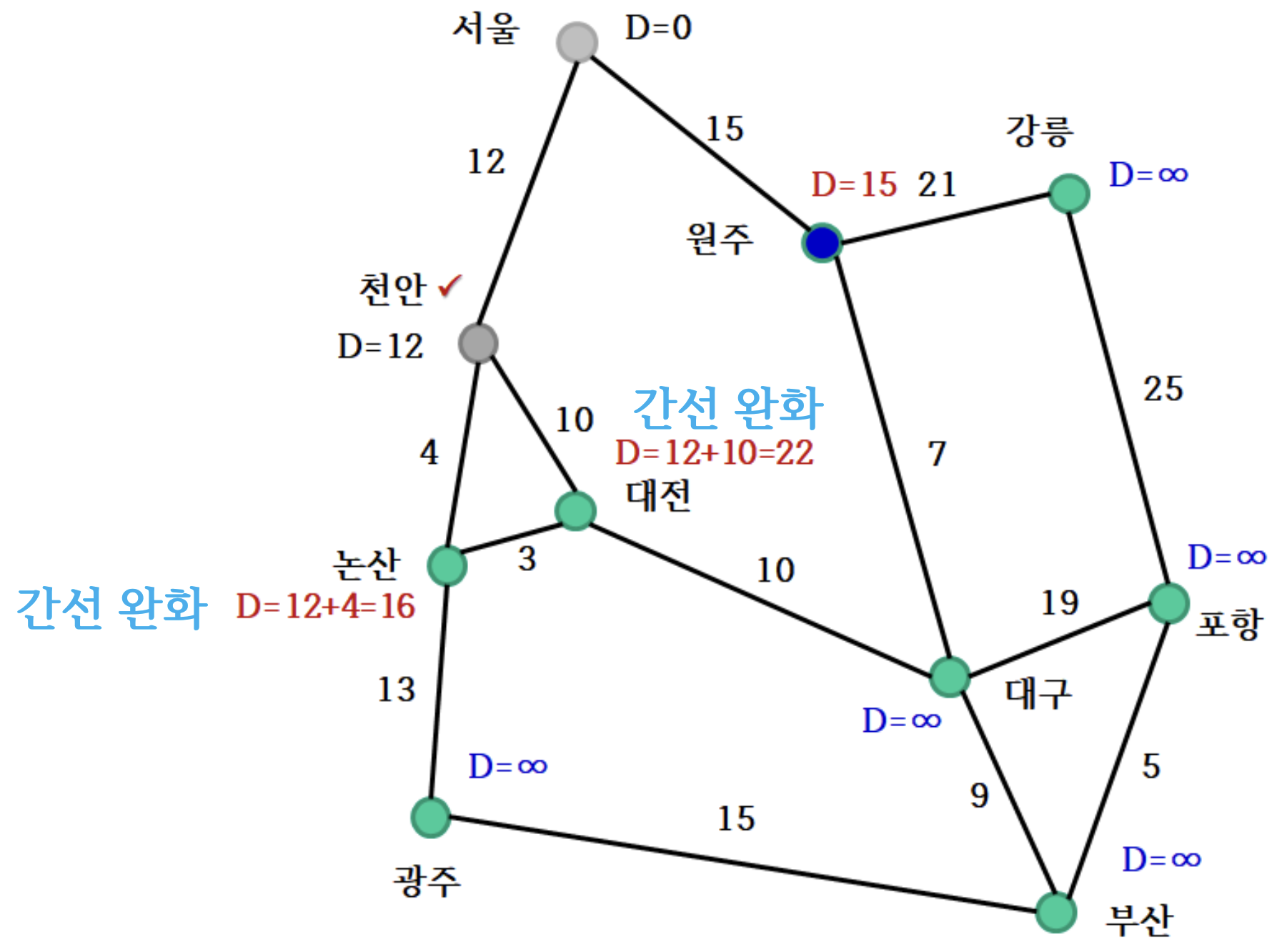
원주, 논산, 대전, 대구, 광주 생략

5. 부산 확정

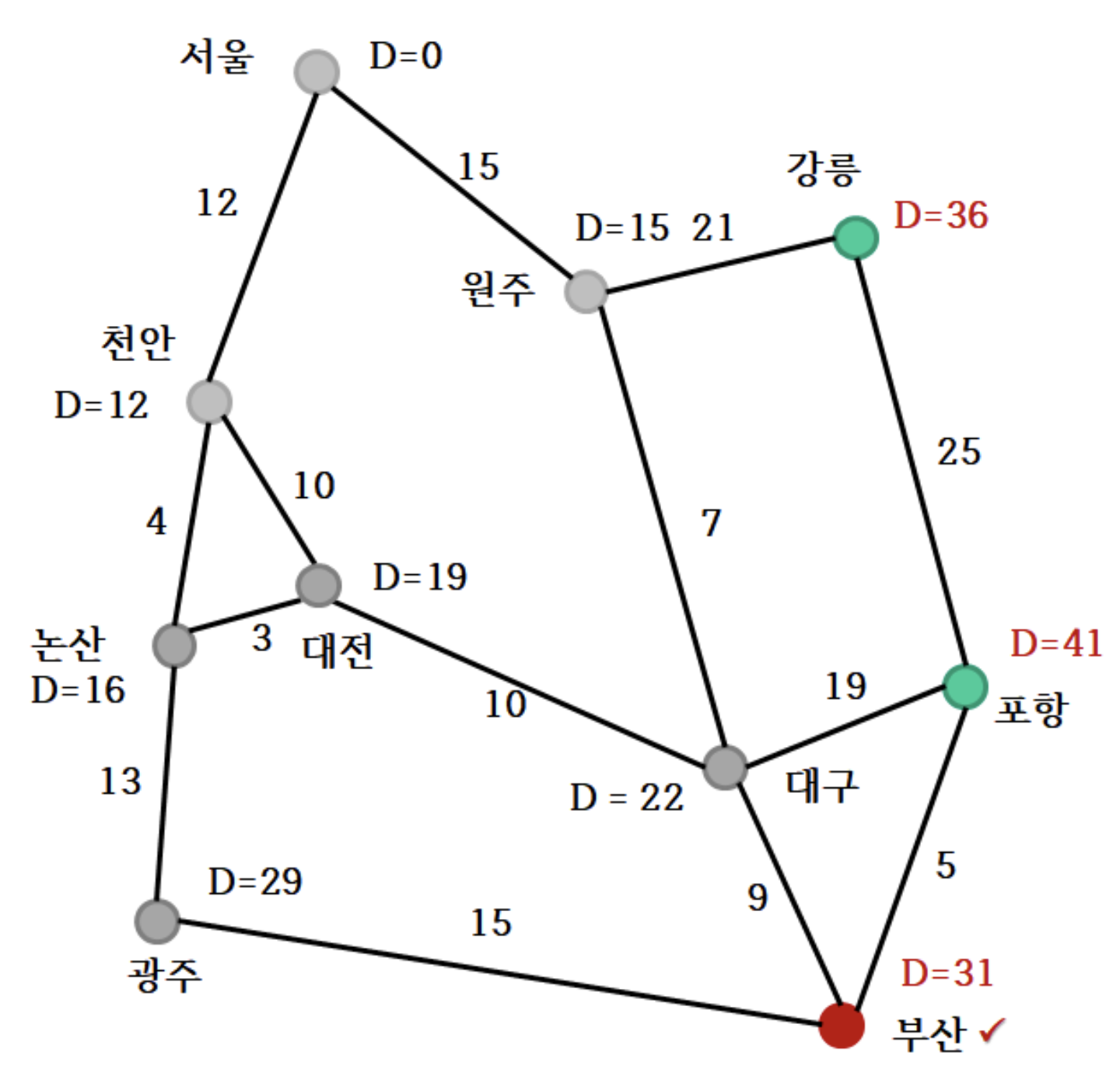
6. 간선 완화

• 대구의 경우 부산을 경유한 거리(31+9=40)가 기존 값(22)보다 크기 때문에 업데이트하지 않는다.
• 포항은 부산을 경유하면 (31+5=36)로 기존 값(41)보다 작아, 최단 거리가 36으로 갱신된다.

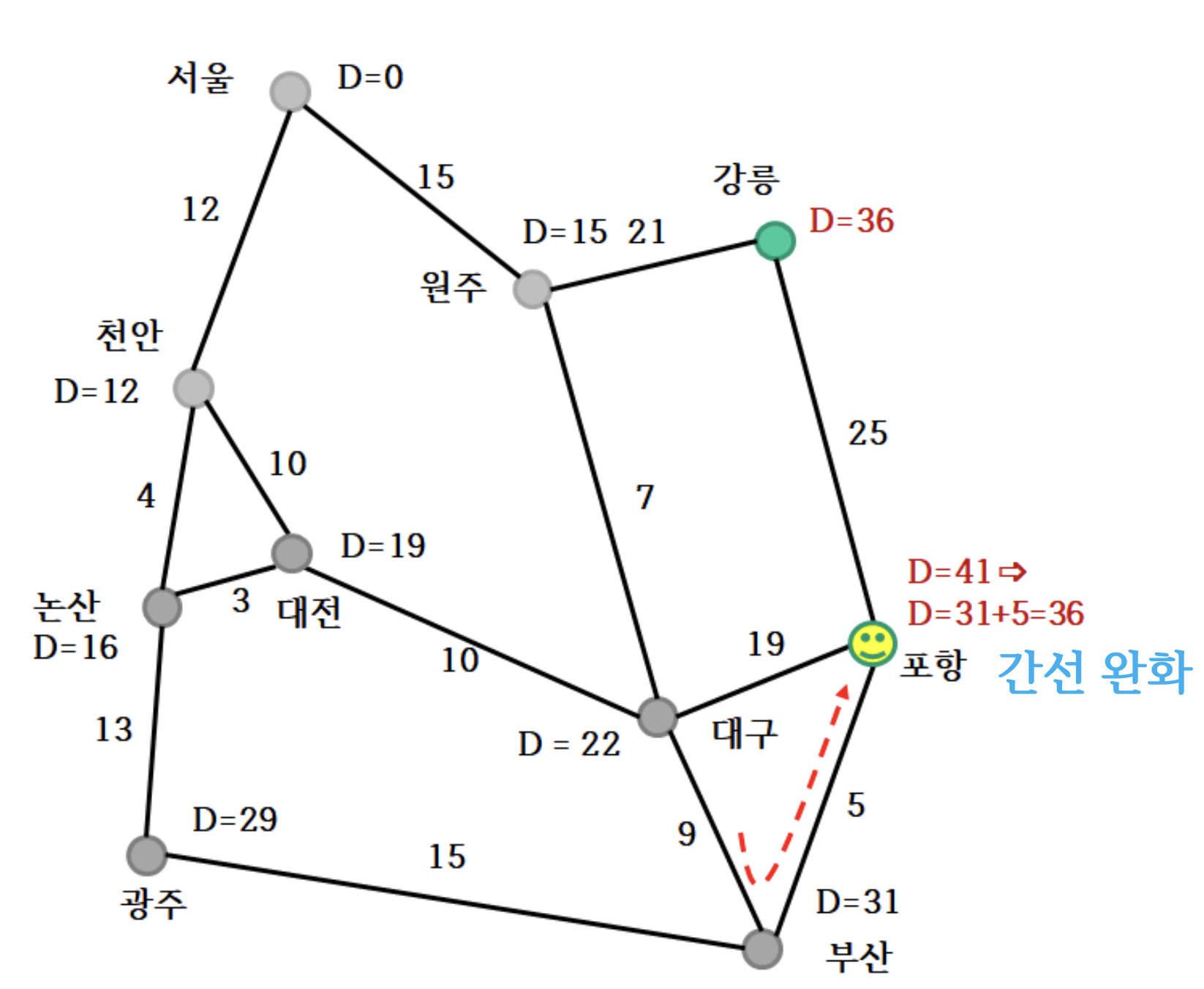
강릉, 포항 생략

4.3.3 Result

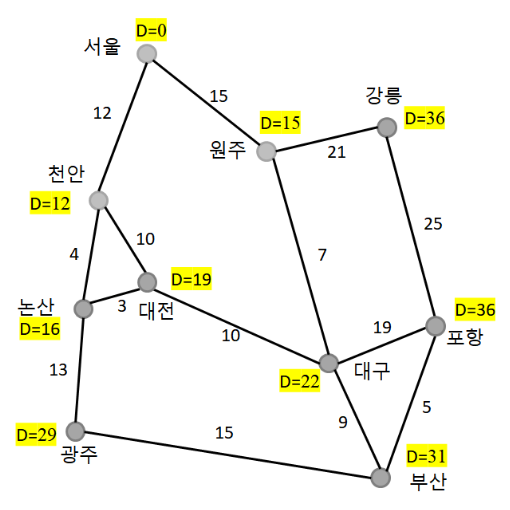
4.3.4 Time Complexity of Dijkstra's algorithm

배열(선형 탐색) 사용

• while문이 (n-1)번 반복
• 각 반복에서 최솟값 탐색 $O(n)$, 인접 거리 갱신도 최악의 경우 $O(n)$
• 전체 시간 복잡도: $O(n^2)$

반복마다 최솟값 탐색 $O(n)$, 간선 완화에 $O(n)$이 걸리니 합이 $O(n)+O(n)=O(n)$이다. 이를 반복 횟수 $n-1$과 곱해 전체 $O(n^2)$가 된다.

최소 힙(우선순위 큐) 사용

• 최솟값 찾기와 갱신이 $O(logn)$
• 간선 수가 $m$일 때 전체 복잡도 $O((n+m)logn)$
  • 간선이 적으면 $O(logn)$, 많으면 $O(mlogn)$

4.3.5 Application

• MapQuest & Google map
• 자동차 네비게이션
• 네트워크와 통신 분야
• 모바일 네트워크
• 산업 공학/경영 공학의 운영 연구
• 로봇 공학
• 교통 공학
• VLSI 디자인 분야

---

4.4 Fractional Knapsack

Knapsack Problem

• n개의 물건이 각각 1개씩 있고,
• 각 물건은 무게와 가치를 가지고,
• 배낭이 한정된 무게의 물건들을 담을 수 있을 때,
• 최대의 가치를 갖도록 배낭에 넣을 물건들을 정하는 문제

Fractional Knapsack Problem

• 물건을 부분적으로 담는 것을 허용
• 그리디 알고리즘으로 해결

0-1 Knapsack Problem

• 부분 배낭 문제의 원형으로 물건을 통째로 배낭에 넣어야 한다.
• 동적 계획 알고리즘, 백트래킹 기법, 분기 한정 기법으로 해결

• 부분 배낭 문제에서는 물건을 부분적으로 배낭에 담을 수 있으므로, 최적해를 위해서 '욕심을 내어' 단위 무게 당 가장 값나가는 물건을 배낭에 넣고, 계속해서 그 다음으로 값나가는 물건을 넣는다.
• 만일 물건을 통째로 배낭에 넣을 수 없으면, 배낭에 넣을 수 있을 만큼만 물건을 부분적으로 배낭에 담는다.

FractionalKnapsack

• Input: n개의 물건, 각 물건의 무게와 가치, 배낭의 용량 C
• Output: 배낭에 담은 물건 리스트 L, 배낭 속의 물건 가치의 합 v

1. 각 물건에 대해 단위 무게 당 가치 계산
2. 단위 무게 당 가치 기준으로 내림차순 정렬된 물건 리스트 S
3. 초기화: $L=\emptyset, w=0, v=0$ // $w$는 배낭에 담긴 물건들의 무게의 합
4. S에서 단위 무게 당 가치가 가장 큰 물건 x를 가져온다.
5. while w + (x의 무게) <= C
6. $\,\,\,\,$ x를 L에 추가
7. $\,\,\,\,$ w = w + (x의 무게)
8. $\,\,\,\,$ v = v + (x의 가치)
9. $\,\,\,\,$ x를 S에서 제거 // 추가했으니 제거
10. $\,\,\,\,$ S에서 단위 무게 당 가치가 가장 큰 물건 x를 가져온다.
11. if C-w > 0 // 배낭에 물건을 부분적으로 담을 여유가 있다면
12. $\,\,\,\,$ 물건 x를 (C-w)만큼만 L에 추가
13. $\,\,\,\,$ v = v + (C-w)만큼의 x의 가치
14. return L, v

while만 있으면 Fractional Kanpsack에서 부분적으로 담는 동작이 자동으로 처리되지 않는다. while 반복문은 물건 전체를 담을 수 있는 경우에만 진행되고, 전체를 못 담는 순간에 반복이 끝나버린다.

4.4.1 Procedure

• 배낭 최대 용량: 40g
• 단위 무게 당 가치 정렬: S=[백금(6만원), 금(5만원), 은(4천원), 주석(1천원)]

1. 백금을 통째로 담는다.
   • 무게 w = 10, 가치 v = 60
2. 금을 통째로 담는다.
   • 무게 w = 25, 가치 v = 135
3. 은을 40-25 = 15 만큼만 담는다.
   • 무게 w = 40, 가치 v = 145 + 0.4*15 = 141

4.4.2 Time Complexity

Line1

• n개의 물건 각각의 단위 무게 당 가치를 계산하는 데 $O(n)$

Line2

• 물건의 단위 무게 당 가치에 대해서 정렬하기 위해 $O(nlogn)$
  • 일반적인 정렬 알고리즘의 시간 복잡도 $O(nlogn)$

Line5~10

• while loop의 수행은 n번을 넘지 않으며, 루프 내부의 수행은 $O(1)$

Line 11~14

• 각 $O(1)$

알고리즘의 시간 복잡도

• $O(n) + O(nlong) + n \times O(1) + O(1) = O(nlogn)$

4.4.3 Application

• 0-1 배낭 문제는 최소의 비용으로 자원 할당하는 문제
  • 조합론, 계산이론, 암호학, 응용 수학 분야에서 기본적인 문제로 다뤄짐
• 버리는 부분 최소화하는 원자재 자르기
• 자산투자 및 금융 포트폴리오에서의 최선의 선택
• Merkle-Hellman 배낭 암호 시스템에서 사용

---

4.5 Set Cover

• n개의 원소를 가진 집합 U가 있고,
• U의 부분집합들을 원소로 하는 집합 F가 주어질 때,
• F의 원소들인 집합들 중에서 어떤 집합을 선택하여 합집하면 U와 같게 되는가?

집합 F에서 선택하는 집합들의 수를 최소화하는 문제

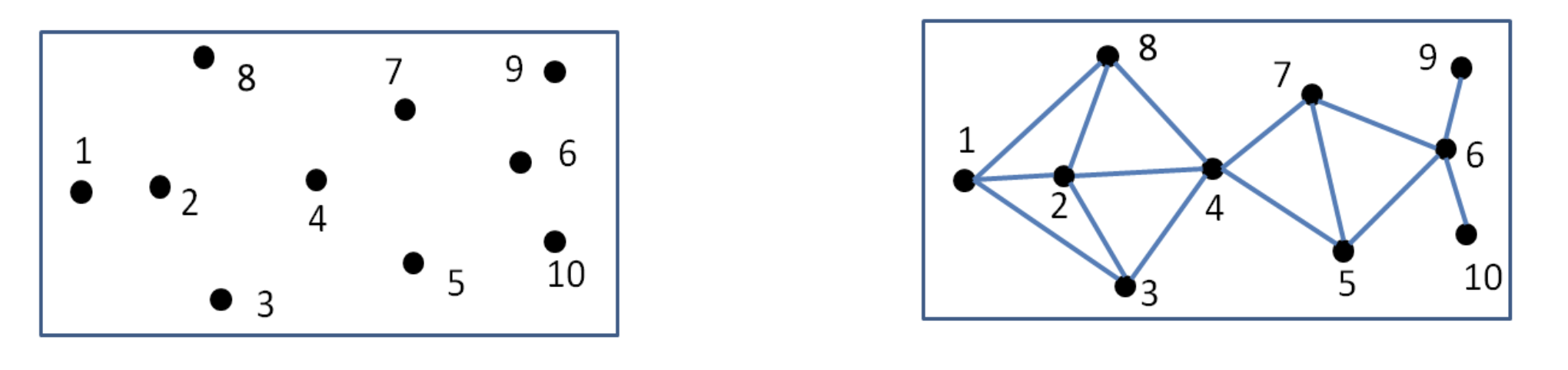
4.5.1 신도시 학교 배치

• 10개의 마을이 신도시에 만들어질 계획
• 다음 조건이 만족되도록 학교 위치 선정
  • 학교는 마을에 위치
• 어느 마을에 학교를 신설해야 학교의 수가 최소가 되는가?

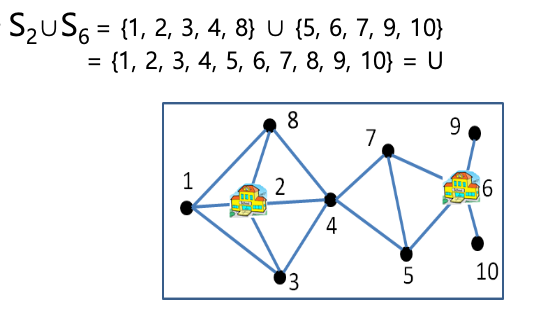
4.5.2 Optimal Solution

• 2번 마을
  • 1, 2, 3, 4, 8 마을의 학생들이 15분 이내에 등교 가능
• 6번 마을
  • 마을 5, 6, 7, 9, 10 커버
• 2번과 6번 마을에 학교를 배치하면 모든 마을이 커버된다.
  • 최소 학교의 수 = 2개

4.5.3 Simple Solution

집합 커버 문제의 최적해는 어떻게 찾아야 할까?

• F에 n개의 집합들이 있다고 가정

가장 단순한 방법

• F에 있는 집합들의 모든 조합을 1개씩 합집합하여 U가 되는지 확인하고,
• U가 되는 조합의 집합 수가 최소인 것을 찾는다.
• $F=\{S_1, S_2, S_3\}$일 경우 모든 조합
  • $S_1, \ S_2, \ S_3,\ S_1 \cup S_2, \ S_1 \cup S_3,\ S_2 \cup S_3, \ S_1 \cup S_2 \cup S_3$
  • 집합이 1개인 경우 3개
  • 집합이 2개인 경우 3개
  • 집합이 3개인 경우 1개
  • 총합은 3+3+1 = 7개 = $2^3-1$개

n개의 원소가 있을 경우

• 최대 $2^n-1$개를 검사, n이 커지면 최적해를 찾는 것은 실질적으로 불가능하다.

이를 극복하기 위한 방법

• 최적해를 찾는 대신에 최적해에 근접한 근사해를 찾는다.
• Approximation solution

결정 문제(집합을 k개 이하로 덮을 수 있는가?): NP-complete
최적화 문제(집합을 최소 개수로 덮는 최소 cover 찾기): NP-hard

SetCover

• Input: $U, F= \{S_i\}, i = 1, ... ,n$
• Output: Set Cover $C$

1. $C = \emptyset$
2. while $U = \emptyset$
3. $\,\,\,\,$ $U$의 원소를 가장 많이 가진 집합 $S_i$를 F에서 선택 // Greedy
4. $\,\,\,\,$ $U=U-S_i$
5. $\,\,\,\,$ $S_i$를 $F$에서 제거하고 $S_i$를 $C$에 추가
6. return $C$

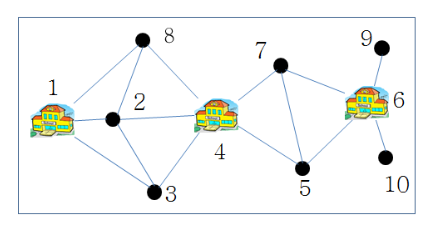
4.5.4 Procedure

$U = \{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 \} \\ F = \{ S_1, S_2, S_3, S_4, S_5, S_6, S_7, S_8, S_9, S_{10} \} \\ S_1 = \{1, 2, 3, 8\} \quad S_2 = \{1, 2, 3, 4, 8\} \quad S_3 = \{1, 2, 3, 4\} \quad S_4 = \{2, 3, 4, 5, 7, 8\} \\ S_5 = \{4, 5, 6, 7\} \quad S_6 = \{5, 6, 7, 9, 10\} \quad S_7 = \{4, 5, 6, 7\} \quad S_8 = \{1, 2, 4, 8\} \\ S_9 = \{6, 9\} \quad S_{10} = \{6, 10\}$

1. U의 원소를 가장 많이 커버하는 집합 $S_4$ 선택
2. $U = U - S_4$
3. $S_4$를 $F$에서 제거하고 C에 추가
   • $C=\{S_4\}$
4. $U=\{1, 6, 9, 10\}$을 가장 많이 커버하는 집합 $S_6$ 선택
5. $U = U - S_6$
6. $S_6$를 $F$에서 제거하고 C에 추가
   • $C=\{S_4, S_6\}$
7. $U=\{1\}$을 가장 많이 커버하는 집합 $S_1$ 선택
8. $U = U - S_1$
9. $S_1$를 $F$에서 제거하고 C에 추가
   • $C=\{S_4, S_6, S_1\}$

Return $C=\{S_4, S_6, S_1\}$

4.5.5 Time Complexity

While-loop 최대 n회 수행

• worst case: 한 번 루프마다 $U$의 원소 1개만 커버된다면 n번 반복

Line3: loop가 1회 수행될 때

• $U$의 원소들을 가장 많이 포함하는 집합 $S$ 찾으려면, 현재 남아있는 $S_i$들 각각을 $U$와 비교하여야
• $S_i$들의 수가 최대 n이라면, 각 $S_i$와 $U$의 비교는 $O(n)$ 시간이 걸리므로 line3은 $O(n^2)$
• 집합 $U$에서 집합 $S_i$의 원소를 제거하므로 $O(n)$
• $S_i$를 $F$에서 제거하고, $S_i$를 $C$에 추가하는 것은 $O(1)$

알고리즘의 시간 복잡도

• $n \times O(n^2) = O(n^3)$
• U의 모든 원소가 커버되어야 하므로 외부 반복 $O(n)$, 가장 많은 원소를 포함하는 집합 S를 찾는 내부 작업 $O(n^2)$ 시간 소요 $\rightarrow O(n) \times O(n^2) = O(n^3)$

4.5.6 Application

• 도시 계획에서 공공 기관 배치
• 경비 시스템: 경비가 요구되는 장소에 CCTV 최적 배치
• 컴퓨터 바이러스 찾기: 병렬로 구역 고를 때
• 대기업의 구매 업체 선정
• 기업의 경력 직원 고용
• 그 외에도 비행기 조종사 스케줄링, 조립 라인 균형화, 정보 검색 등에 활용

4.6 Job Scheduling

작업의 수행 시간이 중복되지 않도록 모든 작업을 가장 적은 수의 기계에 배정하는 문제

주어진 문제 요소

• 작업의 수
  • 입력의 크기(n)이므로 알고리즘을 고안하기 위해 고려되어야 하는 직접적인 요소는 아님
• 각 작업의 시작시간과 종료시간
• 작업의 길이
  • 종료 - 시작

시작시간, 종료시간, 작업 길이에 대한 그리디 알고리즘

• Earliest start time first
• Earliest finish time first
• Shortest job first
• Longest job first

위 4가지 중 첫 번째 알고리즘을 제외하고 나머지 3가지는 항상 최적해를 찾지 못한다.

JobScheduling

• Input: n개의 작업 $t_1, t_2, ... , t_n$
• Output: 각 기계에 배정된 작업 순서

1. 시작 시간으로 정렬한 작업 리스트 $L$
2. while $L \ne \emptyset$
3. $\,\,\,\,$ $L$에서 가장 이른 시작 시간 작업 $t_i$를 가져온다.
4. $\,\,\,\,$ if $t_i$를 수행할 기계가 있으면
5. $\,\,\,\,$ $\,\,\,\,$ $t_i$를 수행할 수 있는 기계에 배정
6. $\,\,\,\,$ else
7. $\,\,\,\,$ $\,\,\,\,$ 새 기계에 $t_i$를 배정
8. $\,\,\,\,$ $t_i$를 $L$에서 제거
9. return 각 기계에 배정된 작업 순서

기계수를 최소화하는 문제이므로 기계 여유가 없으면 새로운 기계 추가

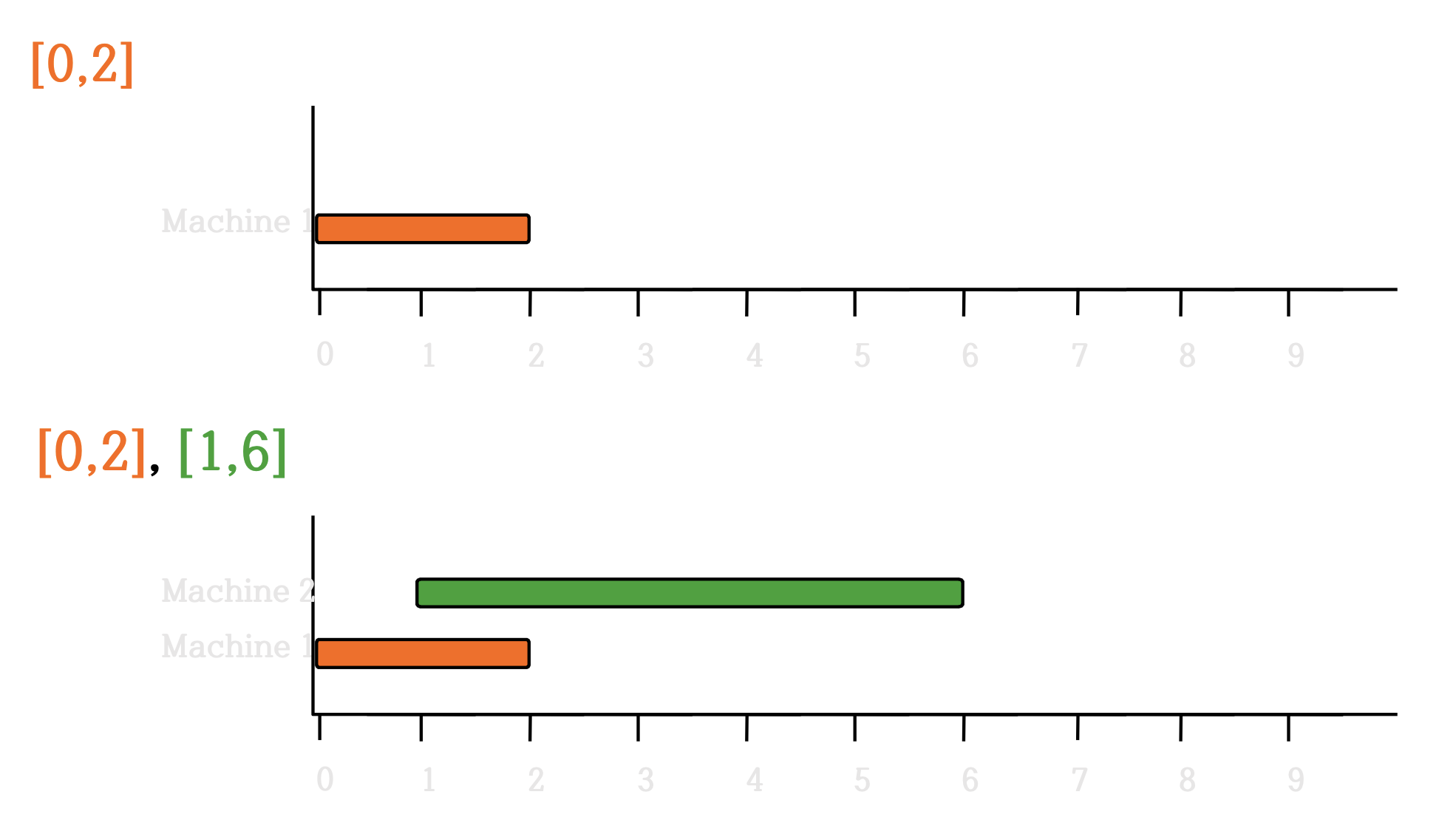
4.6.1 Procedure

$t_1 = [7, 8],\quad t_2 = [3, 7],\quad t_3 = [1, 5],\quad t_4 = [5, 9], \quad t_5 = [0, 2],\quad t_6 = [6, 8],\quad t_7 = [1, 6]$

• $[s, f]$ 에서, s는 시작 시간, f는 종료 시간

정렬

• 시작 시간으로 정렬
• $\quad L = \{ [0,2],\ [1,6],\ [1,5],\ [3,7],\ [5,9],\ [6,8],\ [7,8] \}$

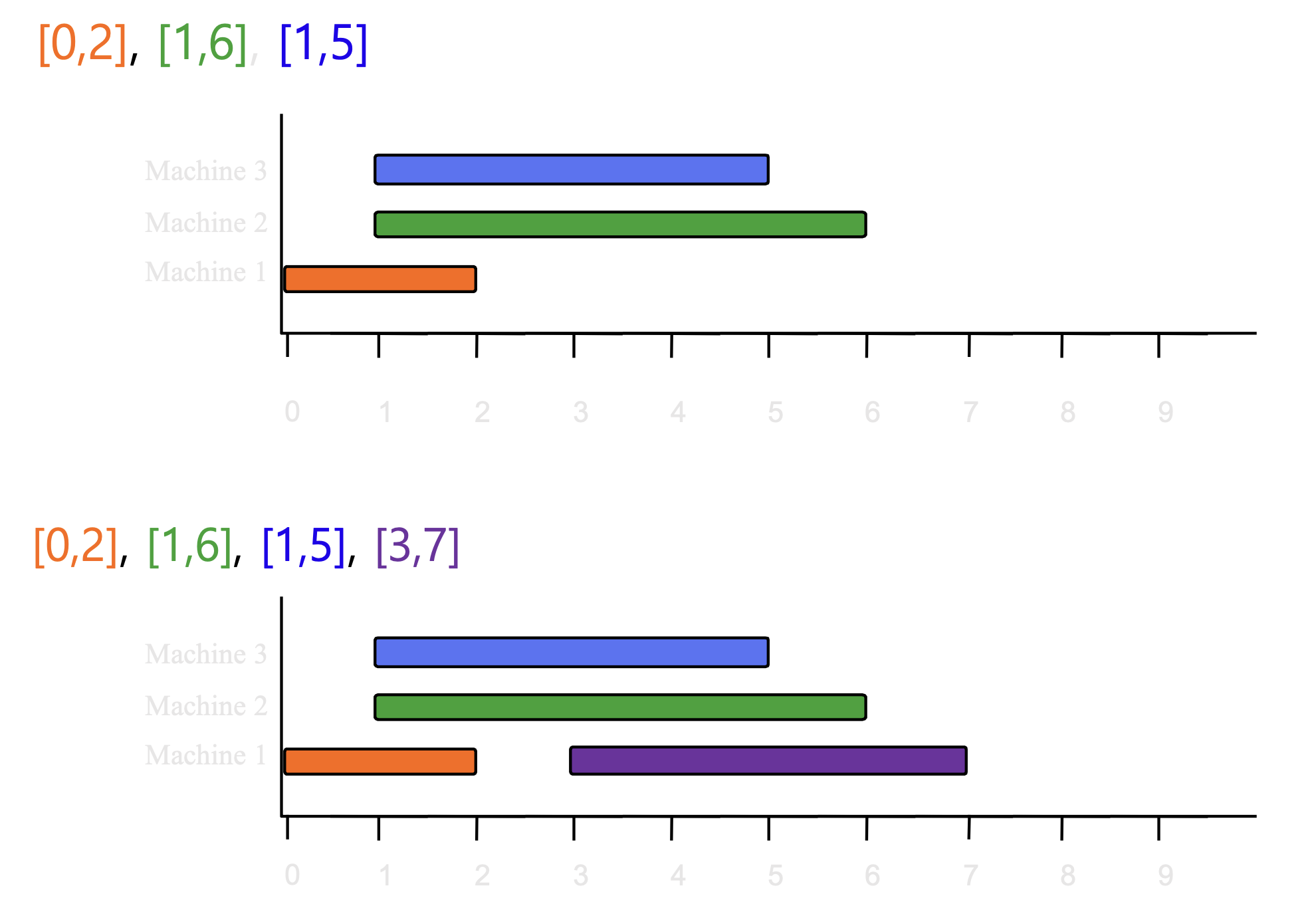
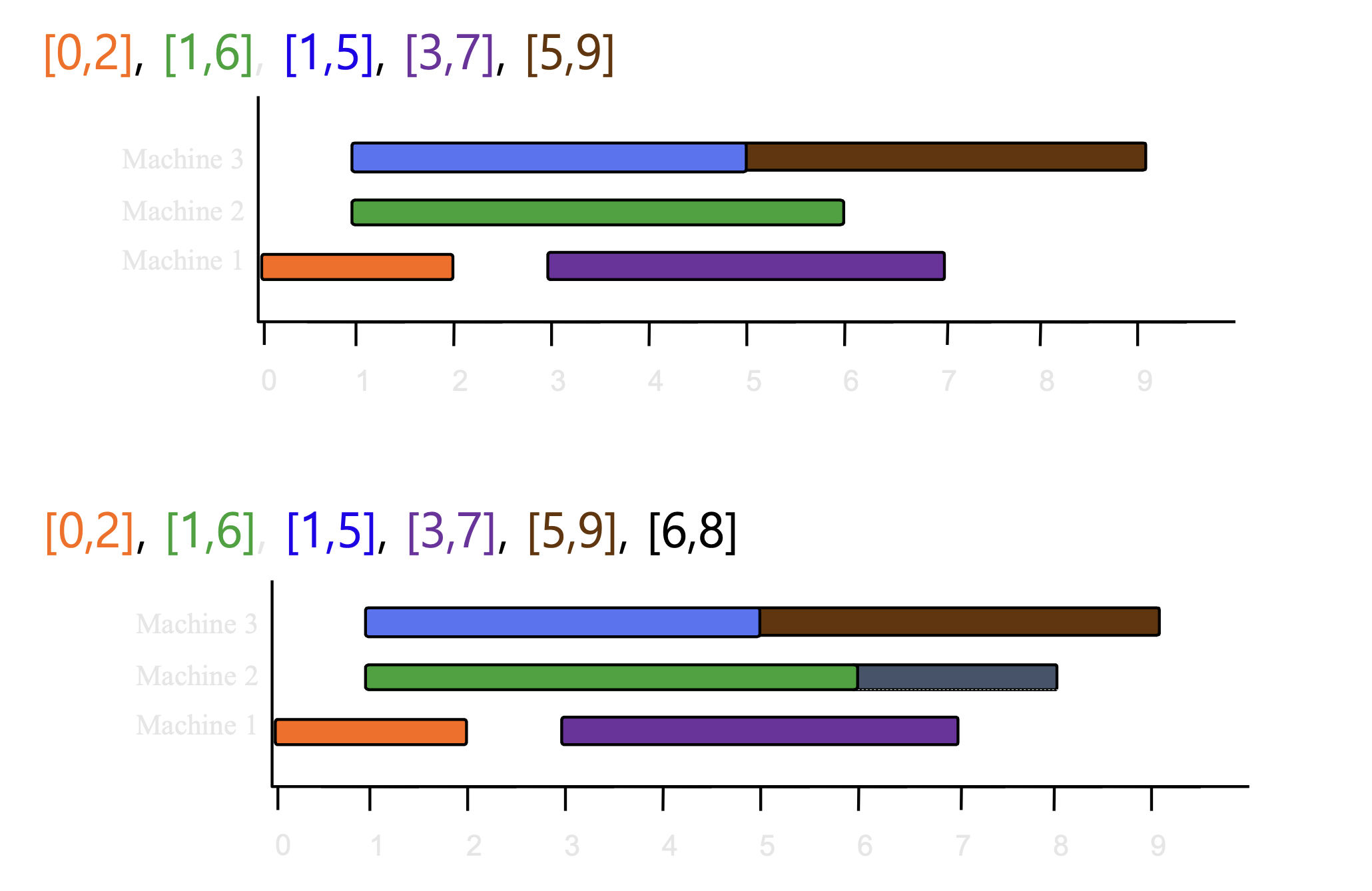
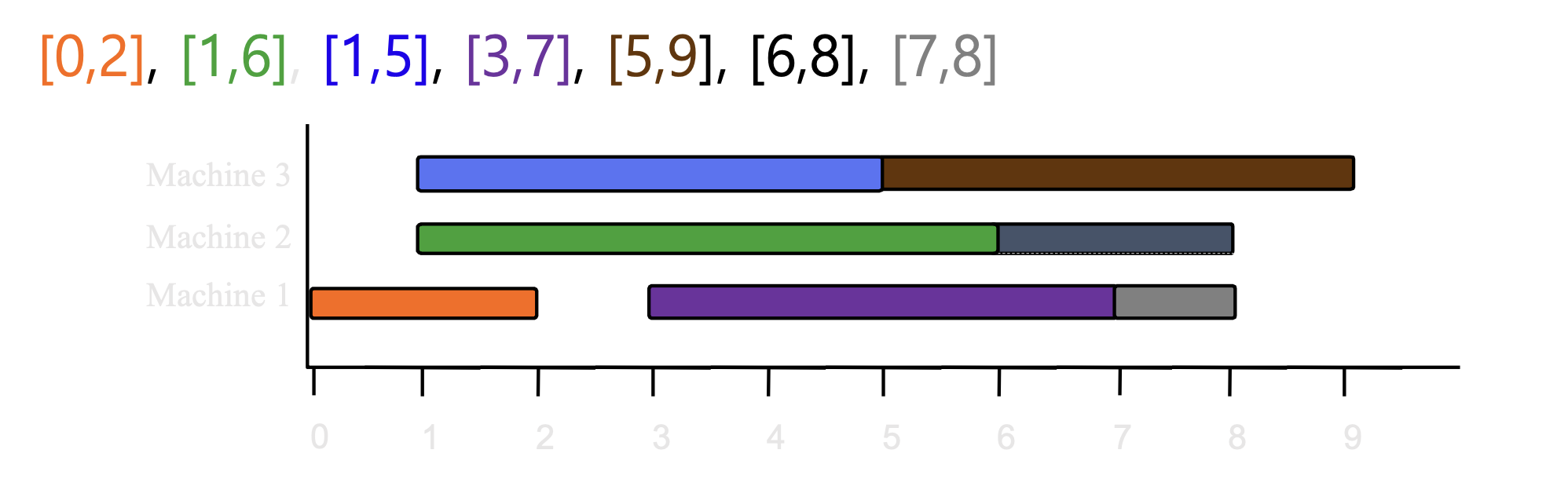
4.6.2 Time Complexity

Line1

• 정렬 시간 $O(nlogn)$

While loop

• 작업을 $L$에서 가져다 수행 가능한 기계를 찾아서 배정하므로 $O(m)$ 시간 소요. 단, m은 사용된 기계의 수
• while loop가 수행된 총 횟수는 $n$번이므로, line 2~9까지는 $O(m) \times n = O(mn)$

Time Complexity

• $O(nlogn)+O(mn)$
  • $m$이 최대 $n$에 가까운 경우 $O(n^2)$으로 볼 수 있다.

4.6.3 Application

• 비즈니스 프로세싱
• 공장 생산 공정
• 강의실/세미나 룸 배정
• 컴퓨터 태스크 스케줄링 등

4.7 Huffman

• 파일을 저장하거나 전송할 때 파일의 크기를 줄이고, 필요 시 원래의 파일로 변환할 수 있으면, 메모리 공간을 효율적으로 사용할 수 있고, 파일 전송 시간 단축 가능
• 파일의 크기를 줄이는 방법을 파일 압축(file compression)이라 한다.

Huffman Compression

• 파일에 빈번히 나타나는 문자에는 짧은 이진 코드 할당, 드물게 나타나는 문자에는 긴 이진 코드 할당
• 변환시킨 문자 코드들 사이에는 접두부 특성(prefix property) 존재
  • 각 문자에 할당된 이진 코드는 어떤 다른 문자에 할당된 이진 코드의 접두부가 되지 않음

접두부 특성의 장점은 코드와 코드 사이를 구분할 특별한 코드가 필요 없다.

입력 파일에 대해 각 문자의 빈도수(문자가 파일에 나타나는 횟수)에 기반을 둔 이진 트리를 만들어서, 각 문자에 이진 코드 할당

• 이러한 이진 코드를 허프만 코드라고 한다.

HuffmanCoding

• Input: 입력 파일의 n개의 문자에 대한 각각의 빈도수
• Output: 허프만 트리

1. 각 문자 당 노드를 만들고, 그 문자의 빈도수를 노드에 저장
2. n 노드의 빈도수에 대해 우선 순위 큐 Q를 만든다.
3. while Q에 있는 노드 수 >= 2
4. $\,\,\,\,$ 빈도수가 가장 적은 노드 (A와 B)를 Q에서 제거
5. $\,\,\,\,$ 새 노드 N을 만들고, A와 B를 N의 자식 노드로 만든다.
6. $\,\,\,\,$ N의 빈도수 = A의 빈도수 + B의 빈도수
7. $\,\,\,\,$ 노드 N을 Q에 삽입
8. return Q // 허프만 트리의 루트 리턴

4.7.1 Procedure

1. 각 문자의 빈도수에 대해 A:450, T:90, G:120, C:270
2. Line2를 수행한 후 Q

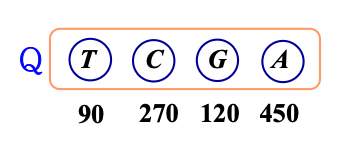
3. Q에서 T와 G를 제거한 후, 새 부모 노드를 Q에 삽입
   

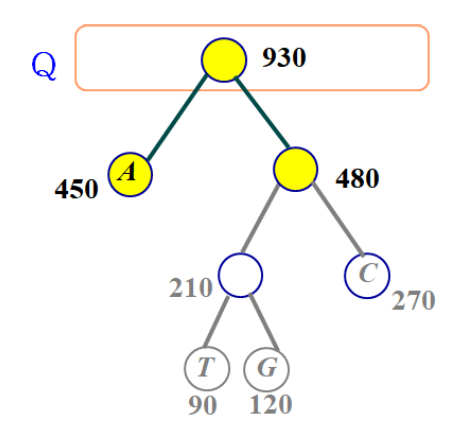
• 반환된 트리를 살펴보면 각 leaf 노드에만 문자가 존재한다.
  • 루트로부터 왼쪽 자식 노드로 내려가면 '0'을, 오른쪽 자식 노드로 내려가면 '1'을 부여하면서, 각 단말에 도달할 때까지의 이진수를 출력하여 이진수를 얻는다.

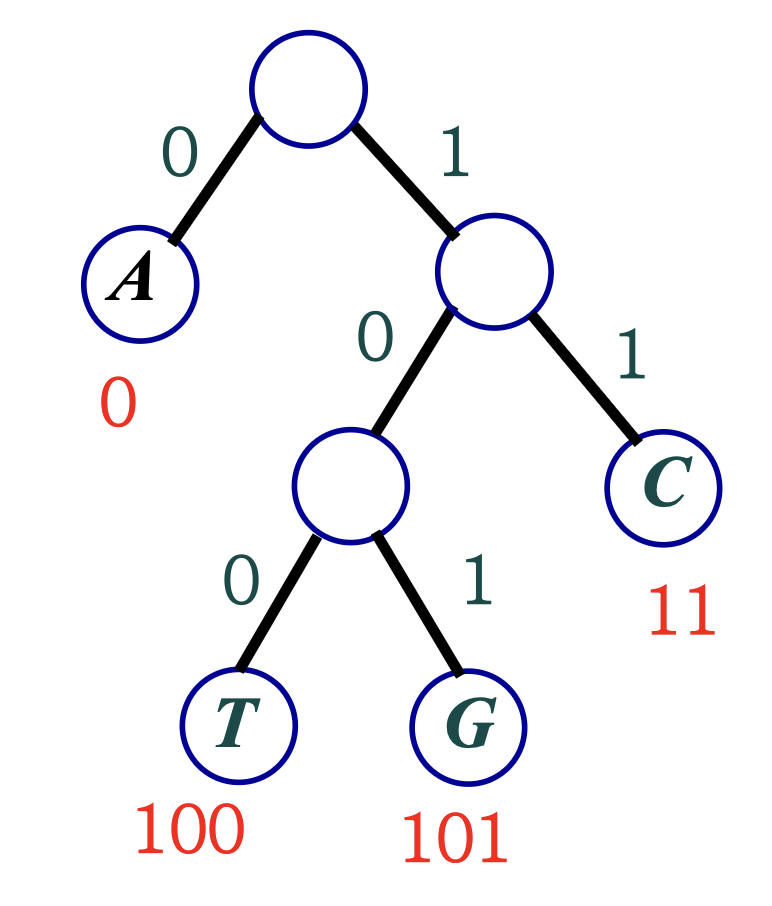
4.7.2 Compressibility

• 예제에서 'A'는 '0', 'T'는 '100', 'G'는 '101', 'C'는 '11'의 코드가 각각 할당된다.
  • 가장 빈도수가 높은 'A'가 가장 짧은 코드를 가져, 루트의 자식이 되어 있고
  • 빈도수가 낮은 문자는 루트에서 멀리 떨어지게 되어 긴 코드를 가진다.
  • 이렇게 얻은 코드는 접두부 특성을 가진다.
• 압축된 파일의 bit 수
  • (450x1)+(90x3)+(120x3)+(270x2) = 1,620 bits
• 아스키 코드로 된 파일 크기
  • (450+90+120+270)x8 = 7,440 bits
    • 2 bit로 비교해도 1,860 bits로 크다.

File Compressibility

• (1,620/7,440)x100 = 21.8%이며, 원래의 약 1/5 크기로 압축

4.7.3 Decoding

• 얻은 하프만 코드로 아래의 압축된 부분에 대해서 압축 해제
  • 10110010001110101010100
• 101 / 100 / 100 / 0 / 11 / 101 / 0 / 101 / 0 / 100
  • G T T A C G A G A T

4.7.4 Time Complexity

Line1

• n개의 노드를 만들고, 각 빈도수를 노드에 저장하므로 $O(n)$ 시간

Line2

• n개의 노드로 우선순위 큐 $Q$를 만든다.
  • 여기서 우선 순위 큐로서 이진 힙 자료구조를 사용하면 $O(n)$ 시간

Line3~7

• 최소 빈도수를 가진 노드 2개를 $Q$에서 제거하는 힙의 삭제 연산과 새 노드를 $Q$에 삽입하는 연산을 수행하므로 $O(logn)$ 시간 소요
• while-loop는 n-1번 반복
  • 왜냐하면 loop가 1번 수행될 때마다 Q에서 2개의 노드를 제거하고, 1개를 Q에 추가하기 때문
  • $(n-1) \times O(logn) = O(nlogn)$

Line8

• 트리의 루트를 번환하는 것이므로 $O(1)$

Time Complexity

• $O(n) + O(n) + O(nlogn) + O(1) = O(nlogn)$

4.7.5 Application

• FAX
• 대용량 데이터 저장
• Multimedia
• MP3 압축
• 정보 이론 분야에서 엔트로피를 계산하는데 활용
  • 이는 자료의 불특정성을 분석하고 예측하는데 이용