4.0 Greedy Algorithm
- 최적화 문제를 해결하는 알고리즘
- 가능한 해들 중에서 가장 좋은(최대 or 최소) 해를 찾는 문제
- 욕심쟁이 방법, 탐욕적 방법, 탐욕 알고리즘
- (입력) 데이터 간의 관계를 고려하지 않고 수행 과정에서 '욕심 내어' 최솟값 또는 최댓값을 가진 데이터를 선택
- 이러한 선택을 '근시안적'인 선택이라고 말한다.
- 한 번 선택하면, 절대로 번복하지 않는다.
- 근시안적 선택으로 부분적인 최적해를 찾고, 이들을 모아서 문제의 최적해를 얻는다.
- 번복하지 않는 특성 때문에 매우 단순하며, 제한적인 문제만이 그리디 알고리즘으로 해결된다.
그리디 알고리즘은 제한적 문제만 최적해를 찾을 수 있어, 일반적으로 근사해를 이용한다.
4.1 Coin Change
- 동전 거스름돈 문제를 해결하는 가장 간단하고 효율적인 방법
- 남은 액수를 초과하지 않는 조건하에 '욕심 내어' 가장 큰 액면의 동전을 취하는 것
- 동전 거스름돈 문제의 최소 동전 수를 찾는 그리디 알고리즘
- 동전의 액면은 500원, 100원, 50원, 10원, 1원
CoinChange
- Input: 거스름돈 액수
- Output: 거스름돈 액수에 대한 최소 동전 수
- change = , n500=n100=n50=n10=n1=0
- while (change 500)
change = change - 500, n500++ // 500원 동전 수 1 증가 - while (change 100)
change = change - 100, n100++ // 100원 동전 수 1 증가 - while (change 50)
change = change - 50, n50++ // 50원 동전 수 1 증가 - while (change 10)
change = change - 10, n10++ // 10원 동전 수 1 증가 - while (change 1)
change = change - 1, n1++ // 1원 동전 수 1 증가 - return (n500+n100+n50+n10+n1) // 총 동전 수 리턴
4.1.1 short-sighted
그리디 알고리즘의 근시안적인 특성
- CoinChange 알고리즘은 남아있는 거스름돈인 change에 대해 가장 높은 액면의 동전을 거스르며,
- 500원 동전을 처리하는 line2에서는 100원, 50원, 10원, 1원 동전을 몇 개씩 거슬러 주어야 할 것인지에 대해서는 전혀 고려하지 않는다.
4.1.2 Procedure
760원의 거스름돈

4.1.3 Problem
160원 동전을 추가로 발행한다면, CoinChange 알고리즘이 항상 최소 동전 수를 계산할 수 있을까?
- 거스름돈이 200원이라면, CoinChange 알고리즘은 160원 동전 1개와 10원 동전 4개로서 총 5개를 리턴
- 200원에 대한 최소 동전 수는 100원짜리 동전 2개
- CoinChage 알고리즘은 항상 최적의 답을 주지 못한다.
- 그러나 실제로는 거스름돈에 대한 그리디 알고리즘이 적용되도록 동전이 발행됨
- CoinChage 알고리즘은 항상 최적의 답을 주지 못한다.

160 x 1 + 10 x 4 보다 100 x 2가 더 좋다. 위 경우에서 최적의 답을 구하기 위해서는 미래를 봐야 가능하다.
Greedy Algorithm은 항상 최적의 해를 제공하지 않는다.
4.2 Minimum Spanning Tree
- 주어진 가중치 그래프에서 사이클 없이 모든 점들을 연결시킨 트리들 중에서 가중치 합이 최소인 트리
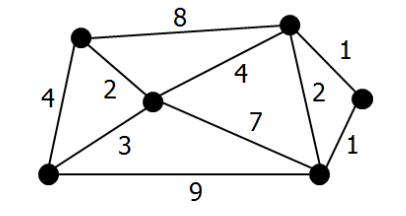
신장 트리 찾는 방법
- 사이클이 없도록 모든 점을 연결시킨다.
그래프의 점의 수 =
- 신장 트리에는 정확히 개의 간선이 있다.
- 트리에 간선을 하나 추가시키면, 반드시 사이클이 만들어진다.
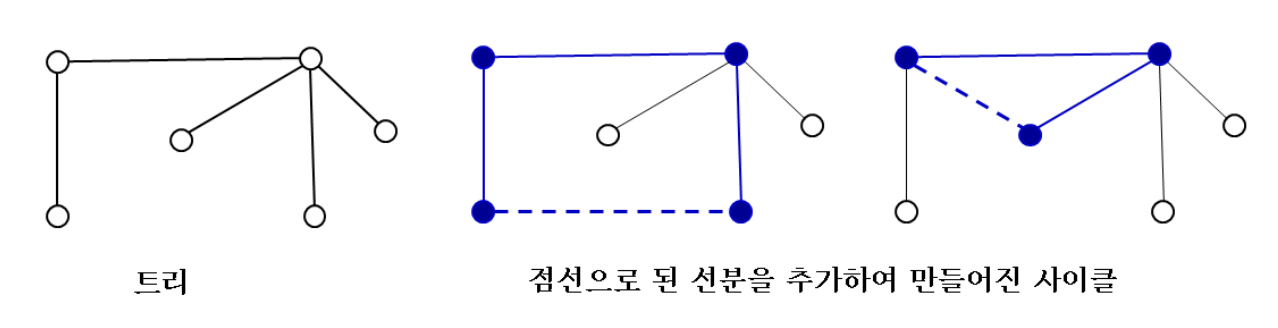
4.2.1 Minimum Spanning Tree Algorithm
Kruskal Algorithm
- 가중치가 가장 작은 간선이 사이클을 만들지 않을 때만 '욕심 내어' 그 간선을 추가한다.
- 간선 중심
Prim Algorithm
- 임의의 점 하나를 선택한 후, 개의 간선을 하나씩 추가시켜 트리를 만든다.
- 점 중심
알고리즘의 입력은 1개의 연결 성분으로 된 가중치 그래프
KruskalMST(G)
- Input: 가중치 그래프
- Output: 최소 신장 트리
- 가중치의 오름차순으로 간선들을 정렬 // = 정렬된 간선 리스트
- // 트리 초기화
- while (의 간선 수 < n-1)
- 에서 가장 작은 가중치를 가진 간선 e를 가져오고, e를 에서 제거
- if (간선 e가 에 추가되어 사이클을 만들지 않으면)
e를 에 추가 - else
e를 버린다. - return
4.2.2 Procedure
1. Line 1
- 오름차순으로 정렬
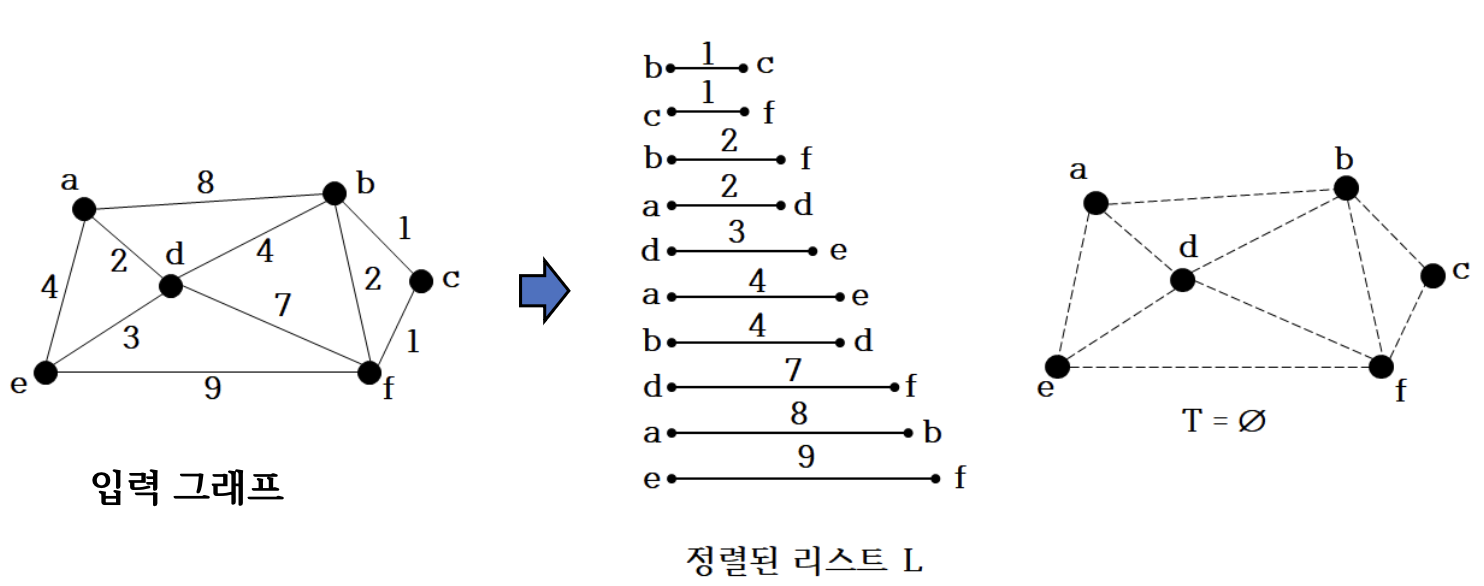
2. Line 3~
- 가중치가 가장 작은 간선 b-c 추가
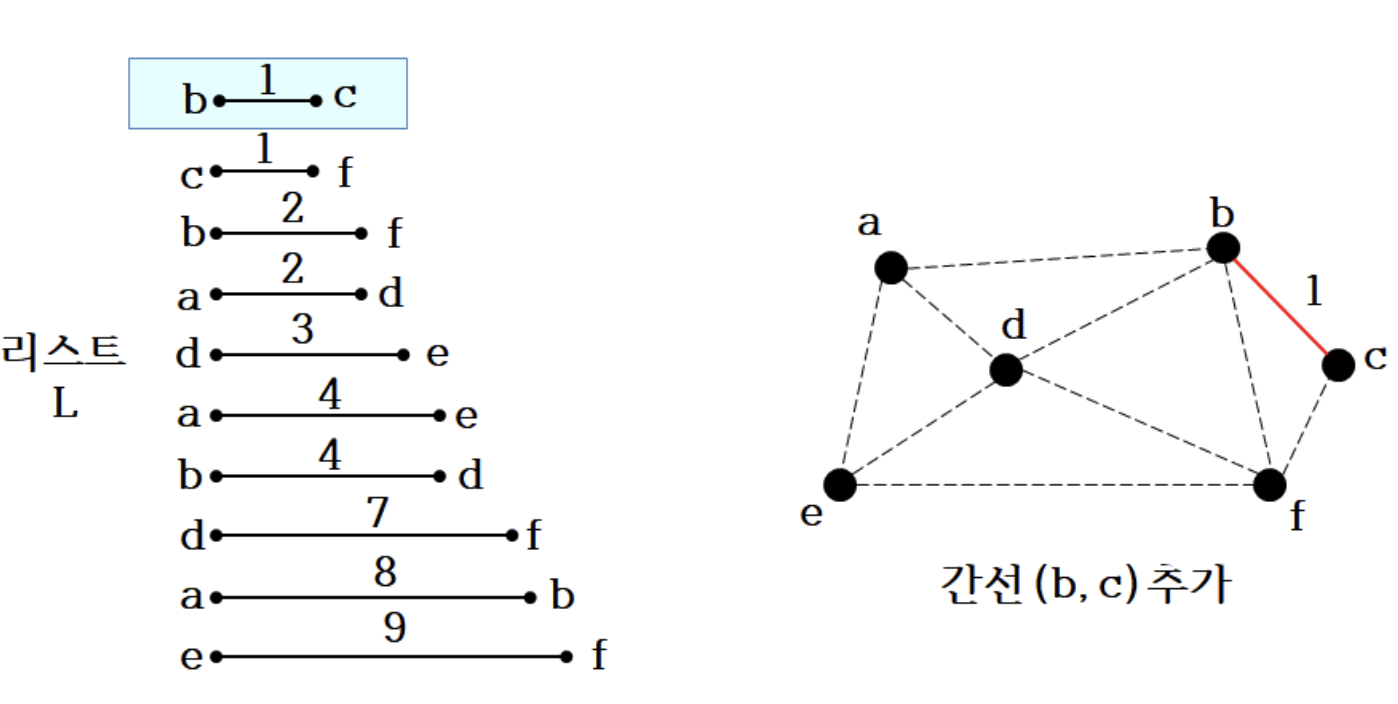
3.
- 간선 (c, f) 추가
4.
- 간선 (b, f) 버림
- 그 다음으로 작은 간선 b-f는 사이클을 형성하므로 버린다.

5, 6.
- 간선 (a, d) 추가
- 간선 (d, e) 추가
7.
- 간선 (a, e) 버림
- a-e 추가 시, 사이클 생성(a-d-e-a)
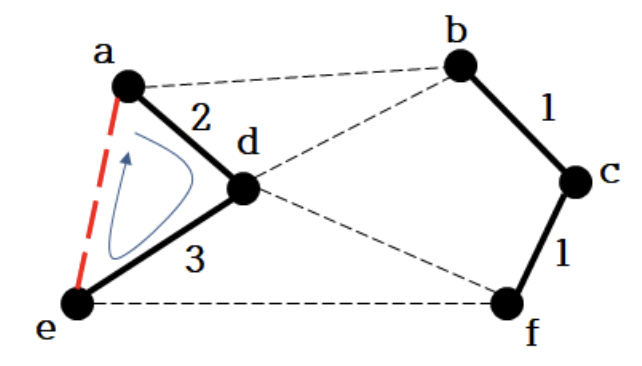
8.
- 간선 (b, d) 추가

Complete
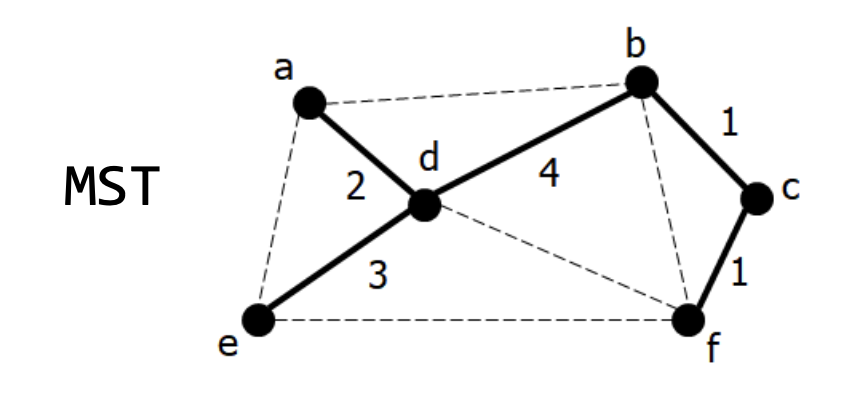
4.2.3 Time Complexity
Line1
- 간선을 정렬하는데 시간
- 단, 은 입력 그래프에 있는 간선의 수
- 일반적인 정렬 알고리즘: Quick sort, Merge sort, Heap sort의 정렬 시간 복잡도
Line2
- 를 초기화하는 것이므로 시간
Line3~8
- While-loop는 최대 번 수행
- 그래프의 모든 간선이 while-loop 내 처리되는 경우
- While-loop 내에서는 로부터 가져온 간선 e가 사이클을 만드는지를 검사하는데 거의 시간
- Union-find: 로 거의
Kruskal's Time Complexity
4.2.4 Prim's MST Algorithm
- 주어진 가중치 그래프에서 임의의 점 하나를 선택한 후 개의 간선을 하나씩 추가시켜 트리 생성
- 실질적으로 점 추가
- 추가되는 간선은 현재까지 만들어진 트리에 연결시킬 때, '욕심 내어' 항상 최소의 가중치로 연결되는 간선
PrimMST(G)
- Input: 가중치 그래프
- Output: 최소 신장 트리
- 에서 임의의 점 p를 시작점으로 선택 // 는 에 있는 와 를 연결하는 간선의 최소 가중치를 저장하기 위한 원소
- for (점 가 아닌 각 점 에 대하여){ // 배열 의 초기화
- if (간선 (p, v)가 그래프가 있으면)
간선 (p, v)의 가중치 - else
} - while (에 있는 점의 수 < n){
- T에 속하지 않는 각 점 에 대하여 가 최소인 점 과 연결된 간선 을 에 추가, 여기서 는 에 속한 점이고, 점 도 에 추가
- for (에 속하지 않은 각 점 에 대해서){
- if (간선 의 가중치 < )
간선 의 가중치 // 를 갱신
}
} - return
Prim 알고리즘에서 배열은 시작점에서 직접 연결된 정점들의 가중치만 우선 저장하고, 나머지 정점은 으로 초기화한 후, 본격적인 알고리즘 루프로 들어간다.
4.2.5 Procedure
1. Line1
- 임의의 점 선택, 으로 초기화
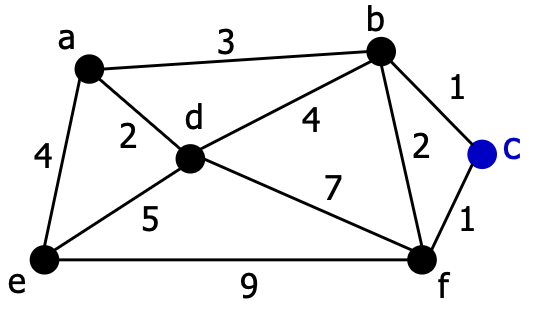
2. Line2~6
- 시작점 와 간선으로 연결된 각 점 에 대해서, 를 각 간선의 가중치로 초기화
- 나머지 각 점 에 대해서, 는 로 초기화

3. Line7
- 로 초기화
4. Line8~9
- 에 가장 가까운 점 를 추가
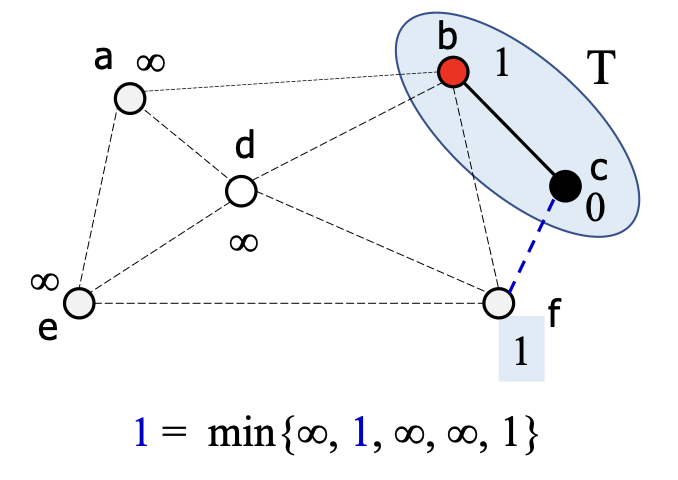
5.
- 에 연결된 와 의 와 갱신
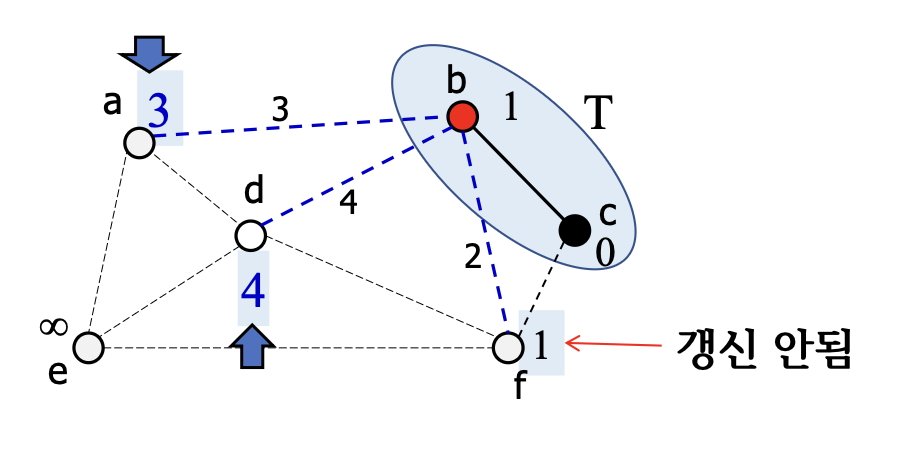
가 추가되면서 와 연결된 점에서의 가중치를 갱신한다.
6.
- 에 가장 가까운 점 추가
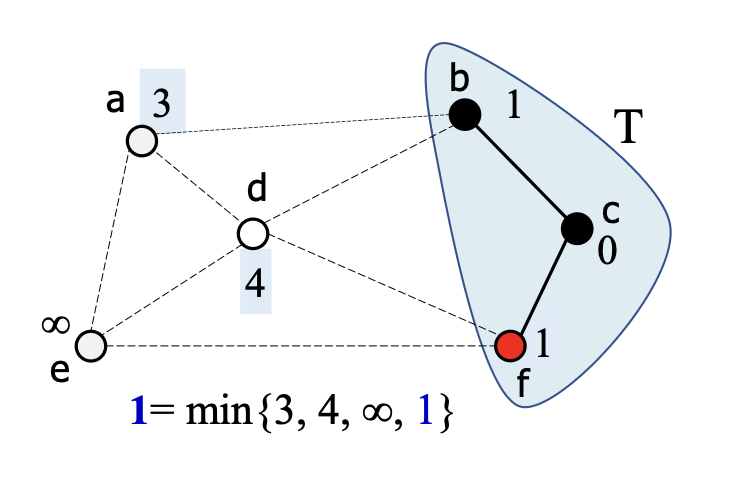
7.
- 에 연결된 의 갱신
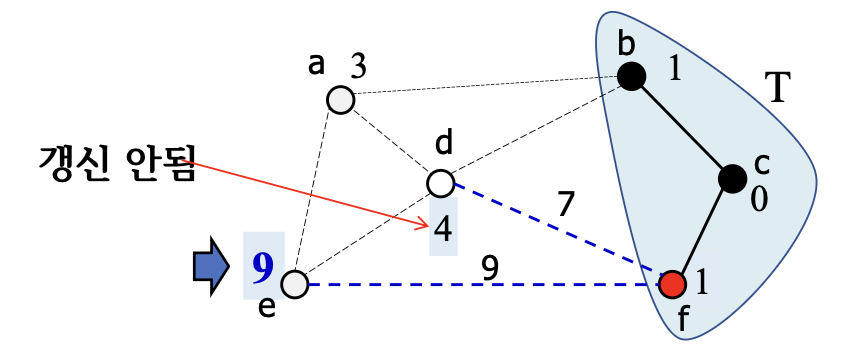
8.
- 를 에 추가
- 에 연결된 의 갱신

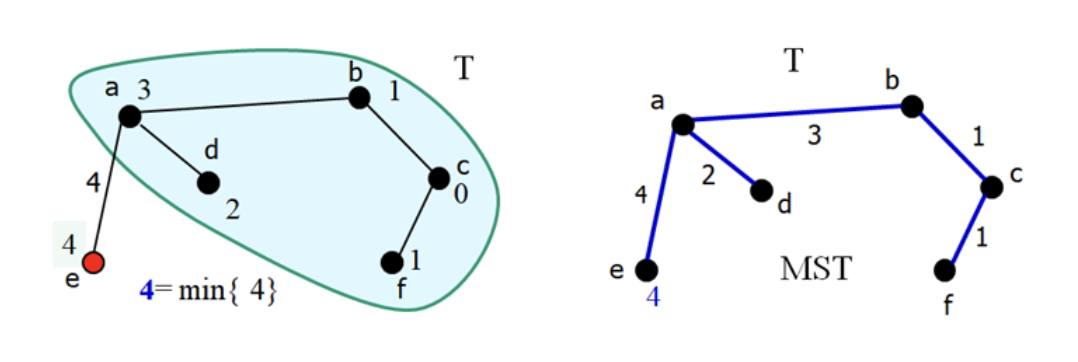
9.
- 를 에 추가
- 가 새롭게 갱신되면서 최소 점이 되었음
- 에 연결된 의 갱신
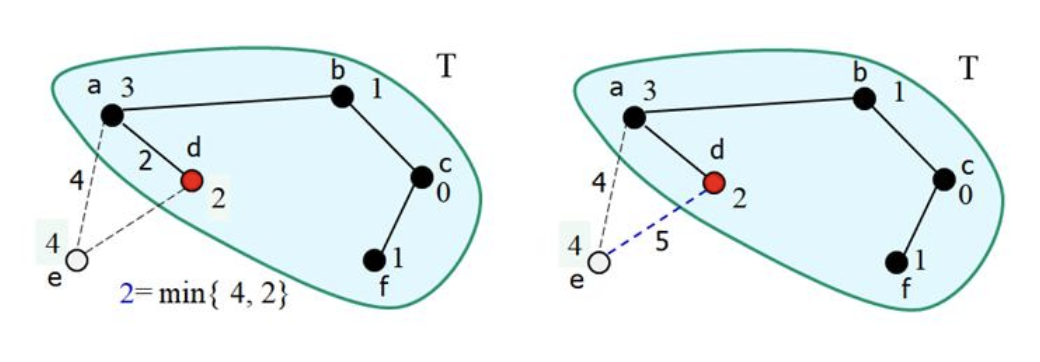
10. Complete
- 를 에 추가
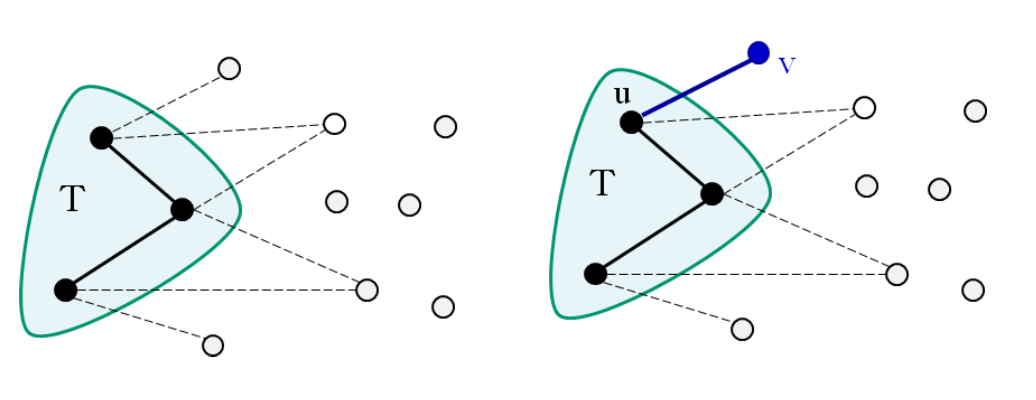
4.2.6 Why PrimMST is none cycle?
- 프림 알고리즘은 밖에 있는 점을 항상 추가하므로 사이클이 만들어지지 않는다.
4.2.7 Time Complexity
while-loop 회 반복
- 트리의 개의 점을 만들기 위해 개의 간선 추가
- 1회 반복될 때, 트리에 속하지 않은 모든 정점 중 을 찾아야 한다.
- 배열에서 선형 탐색이므로 소요
Prim's Time Complexity
- 전체 시간 복잡도:
- 최소 힙(Binary heap)을 사용하여 을 찾으면
- 은 간선 수, 은 배열 크기
- 따라서 간선 수가 이면
- 일반적인 경우:
4.2.8 Kruskal vs. Prim
Kruskal Algorithm
- 간선이 1개씩 에 추가되는데, 이는 마치 개의 점들이 각각의 트리인 상태에서 간선이 추가되면 2개의 트리가 1개의 트리로 합쳐지는 것과 같다.
- 이를 반복하여 1개의 트리인 를 생성
- 개의 트리들이 점차 합쳐져서 1개의 신장 트리 생성
- Sparse 그래프에서 특히 효율적이다.
- - (간선)이 에 비해 작을 때 더 빠름
Sparse(간선이 적은) 그래프, 이 작을수록 더 빠르다.
Prim Algorithm
- 가 점 1개인 트리에서 시작되어 간선을 1개씩 추가
- 1개의 트리가 자라나서 신장 트리가 된다.
- Dense 그래프에서 효율이 좋다. 이 클수록 힙 구현에서의 성능이 우위하다.
- 또는
4.2.9 Application
- 최소 비용으로 선로 또는 파이프를 설치하는데 활용
- 인터넷 광 케이블 선로
- 케이블 TV 선로
- 전화 선로
- 송유관로
- 가스관로
- 배수로
