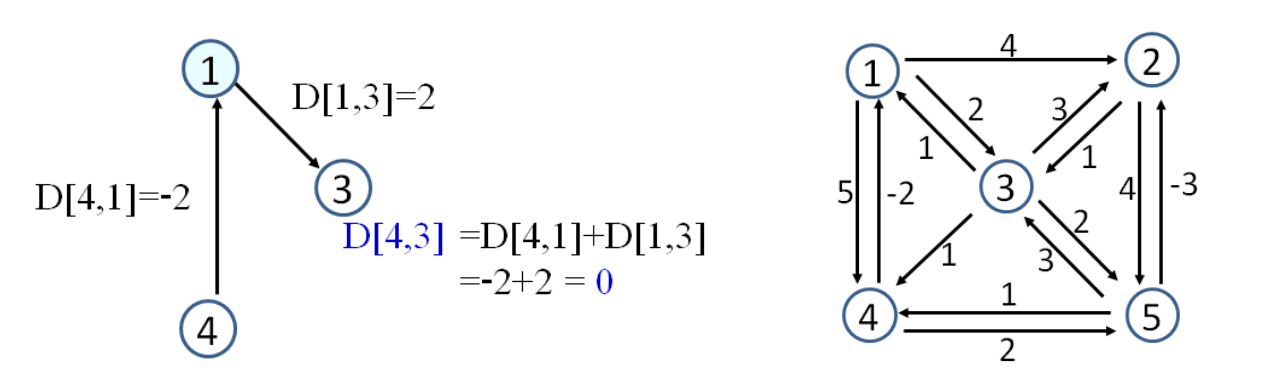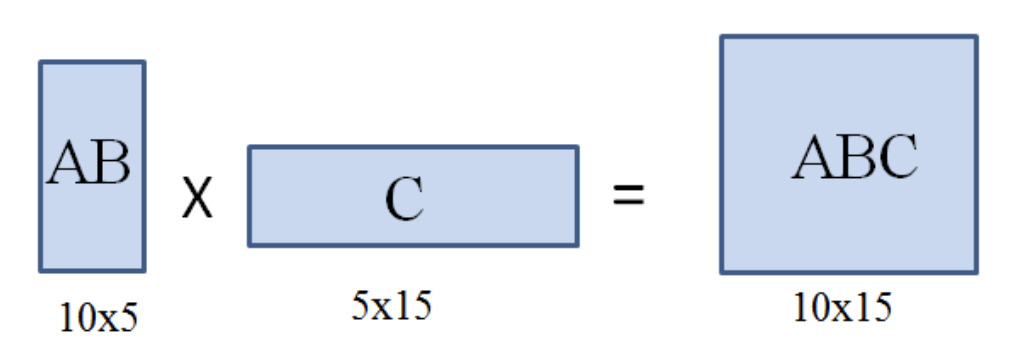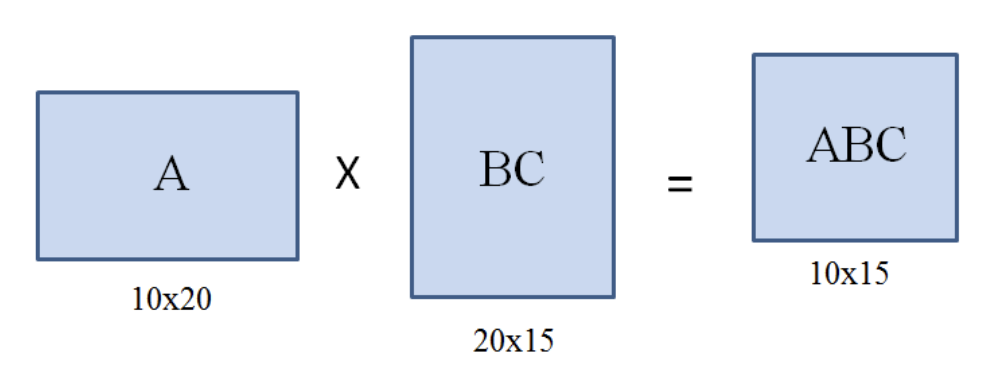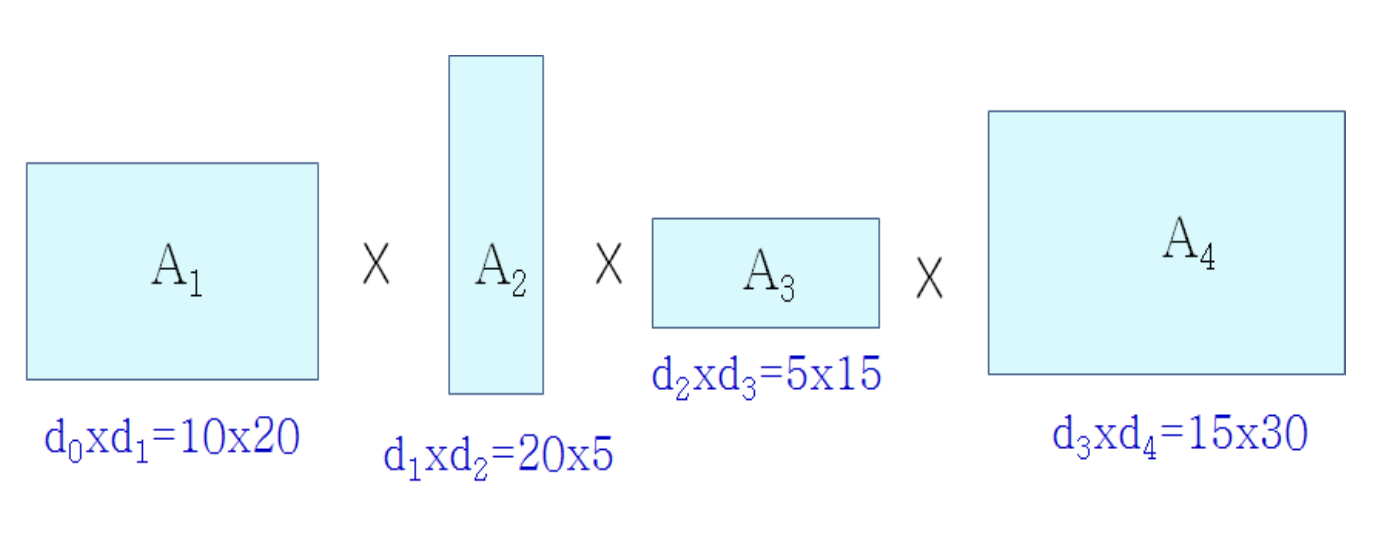5. Dynamic Programming (1)

Dynamic Programming Algorithm

• 입력 크기가 작은 부분 문제들을 해결한 후에(분할)
• 그 해들을 이용하여 보다 큰 크기의 부분 문제들을 해결해
• 최종적으로 원래 주어진 입력의 문제를 해결

5.0 DP vs Divide and Conquer

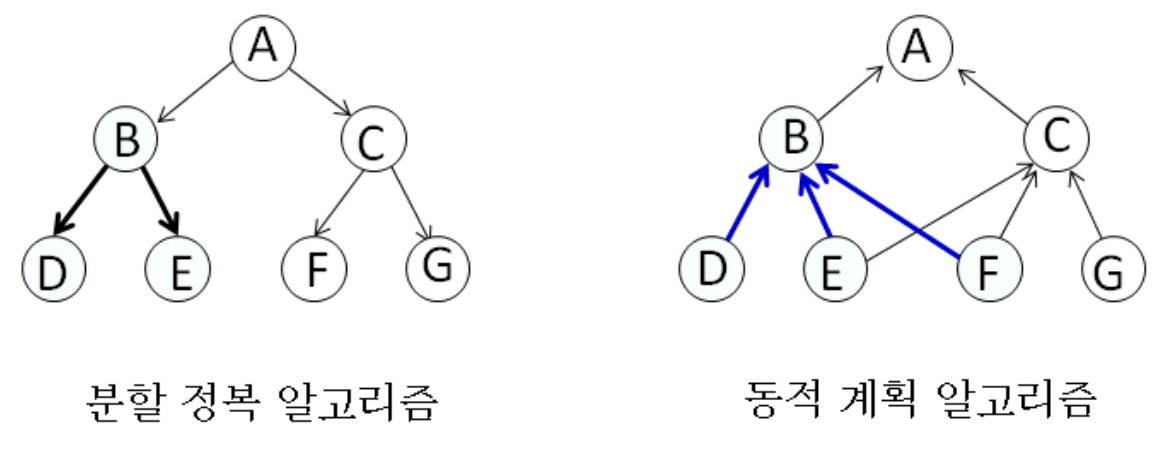
Divide and Conquer Algorithm

• 부분 문제의 해를 중복으로 사용하지 않음

DP Algorithm

• 부분 문제들 사이에 의존적 관계 존재
  • 작은 부분 문제의 해가 보다 큰 부분 문제를 해결하는데 사용됨
  • 문제 또는 입력에 따라 다르고, 대부분의 경우 뚜렷이 보이지 않아서 함축적 순서(implicit order)라고 함

두 알고리즘은 하위 문제를 푸는 구조는 비슷하지만, 합쳐 나가는 방식에서 본질적인 차이가 있다.

DP는 최적 부분 구조와 중복 부분 문제라는 두 가지 성질을 가진 문제에 적용되며, 재귀적으로 부분 문제를 푸는 분할 정복과 개념적으로 비슷하지만, 중복 계산을 피하기 위해 계산한 결과를 테이블에 저장한다는 점이 다르다.

5.1 All Pairs Shortest Paths

각 쌍의 점 사이의 최단 경로를 찾는 문제

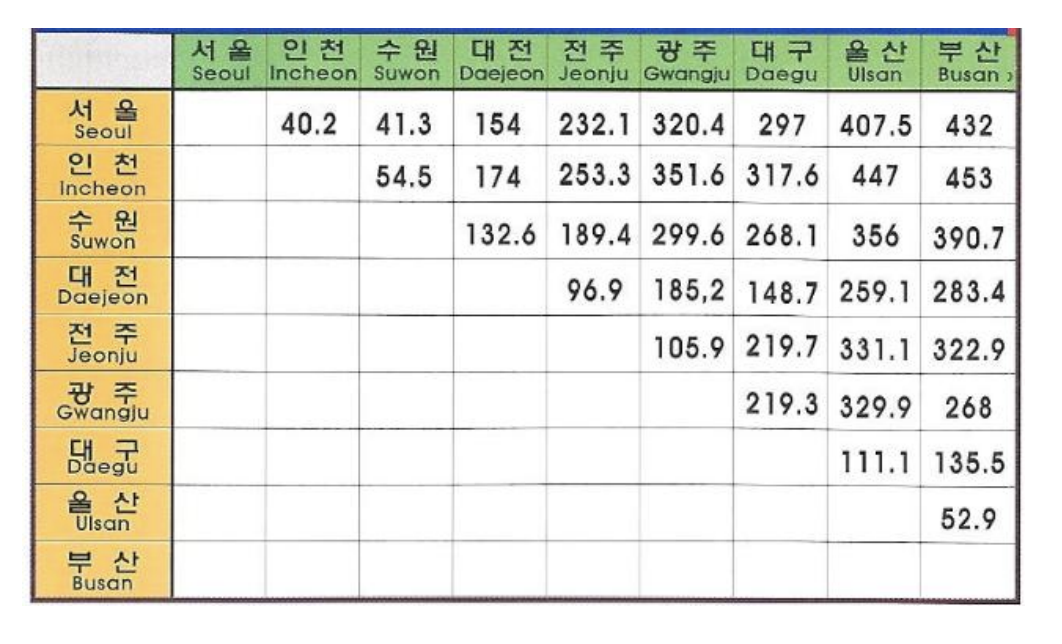
• Dijkstra의 최단 경로 알고리즘을 이용하면
  • 각 점을 시작점으로 정하여 알고리즘 수행
  • 시간 복잡도는 $n \times O(n^2) = O(n^3)$, $n$은 점의 수

5.1.1 Floyd-Warshall Algorithm

• 시간 복잡도 $O(n^3)$
• Dijkstra를 $n$번 사용할 때의 시간 복잡도와 동일
• Floyd 알고리즘은 매우 간단하여 잘 구현하면 Dijkstra보다 빠름

모든 노드에 대한 Dijkstra, input으로 시작점이 필요 없다.

5.1.2 DP Idea

• 작은 그래프에서 부분 문제들 찾기
• 3개의 점이 있는 경우, $a$에서 $c$까지의 최단 경로를 찾으려면 2가지 경로
  • $a$에서 $c$로 직접 가는 경로
  • $b$를 경유하는 경로

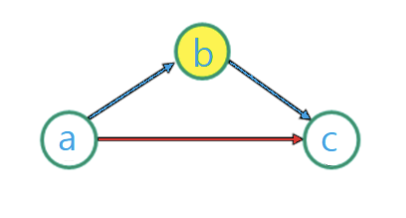
점 $1, 2, ...,n$인 경우, 모든 점을 경유 가능한 점들을 고려하면서 모든 쌍의 최단 경로의 거리를 계산

5.1.3 SubProblem

그래프의 점이 $1,2,3, ... ,n$일 때

• $D_{ij}^k=$ 점 ${1,2,3, ... ,k}$를 경유 가능한 점으로 고려하여, 점 $i$에서 점 $j$까지의 모든 경로 중 가장 짧은 경로의 거리
  • 점 $1$에서 점 $k$까지의 모든 점을 반드시 경유하는 경로를 의미하는 것이 아니다.
• $D_{ij}^k$는 ${1,2,3, ... ,k}$을 하나도 경유하지 않으면서 점 $i$에서 직접 점 $j$에 도달하는 간선 $(i, j)$가 가장 짧은 거리일 수도 있음
• $k \neq i, k \neq j$이고 $k=0$인 경우, 점 $0$은 그래프에 없으므로 어떤 점도 경유하지 않는다는 것을 의미
  • $D_{ij}^0=$ 간선 $(i, j)$의 가중치

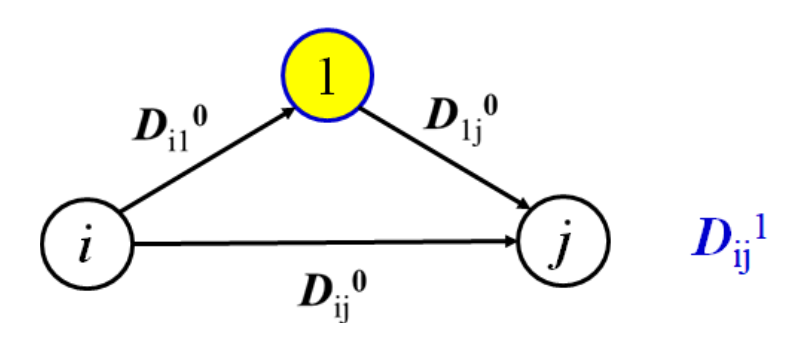
$D_{ij}^1$

• 점 i에서 점 j까지 점 1을 경유하는 경우와 직접 가는 경로 중에서 짧은 경로의 거리
• 모든 점 i와 j에 대해 $D_{ij}^1$를 계산하는 것이 가장 작은 부분 문제
• $i \neq 1, j \neq 1$
  • $i$와 $j$는 출발점 혹은 도착점이므로 $k$와 같을 수 없다.
• $D_{ij}^1 = min(D_{ij}^0, D_{i1}^0 + D_{1j}^0)$

$D_{ij}^2$

• 점 $i$에서 점 2를 경유하여 $j$로 가는 경로의 거리와 $D_{ij}^1$ 중에서 짧은 경로의 거리
• $i \neq 2, j \neq 2$
• $D_{ij}^2 = min(D_{ij}^1, D_{i2}^1 + D_{2j}^1)$

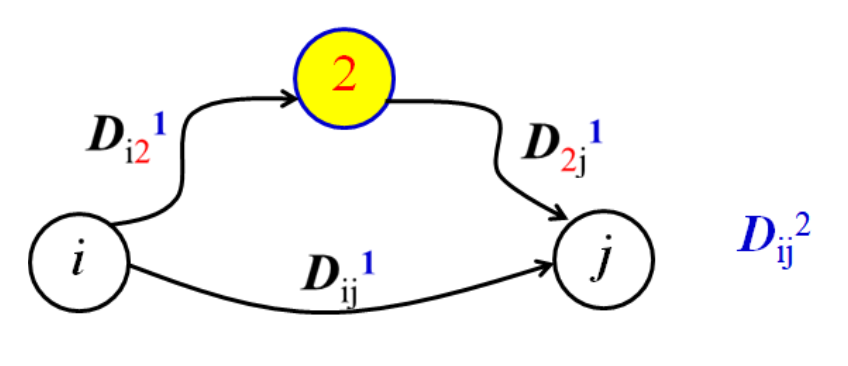
$D_{ij}^k$

• 점 $i$에서 점 $k$를 경유하여 $j$로 가는 경로의 거리와 $D_{ij}^{k-1}$ 중에서 짧은 경로의 거리
• 점 $k$를 경유하는 경로의 거리는 $D_{ik}^{k-1} + D_{kj}^{k-1}$이고, $i \neq k, j \neq k$

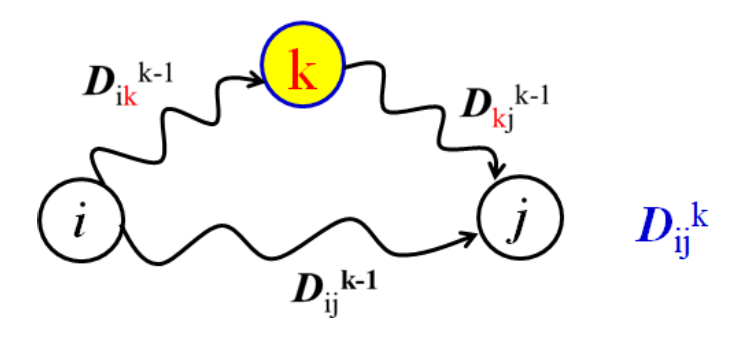
$D_{ij}^k = min(D_{ij}^{k-1}, D_{ik}^{k-1} + D_{kj}^{k-1})$

$D_{ij}^n$

• 모든 점을 경유 가능한 점들로 고려한 모든 쌍 $i$와 $j$의 최단 경로의 거리
• 플로이드의 모든 쌍 최단 경로 알고리즘은 $k$가 $1$에서 $n$이 될 때까지 $D_{ij}^k$를 계산해서 $D_{ij}^n$을 찾는다.

AllPairsShortest

• Input: 2차원 배열 $D$,
  • $D[i, j]=$ 간선 $(i, j)$의 가중치
  • 만일 간선 $(i, j)$가 없으면 $D[i, j]= \infin$
  • 모든 $i$에 대하여 $D[i, i]= 0$
• Output: 모든 쌍 최단 경로의 거리를 저장한 2차원 배열 $D$

1. for $k=1$ to $n$
2. $\,\,\,\,$for $i=1$ to $n(i \neq k)$
3. $\,\,\,\,$$\,\,\,\,$for $j=1$ to $n(j \neq k, j \neq i)$
4. $\,\,\,\,$$\,\,\,\,$$\,\,\,\,$ $D[i, j] =$ min $\{D[i, k] + D[k, j], D[i, j]\}$

중간자 노드인 k를 outer로 두고 source, dest를 바꾸면서 구한다.

부분 문제 간의 함축적 순서

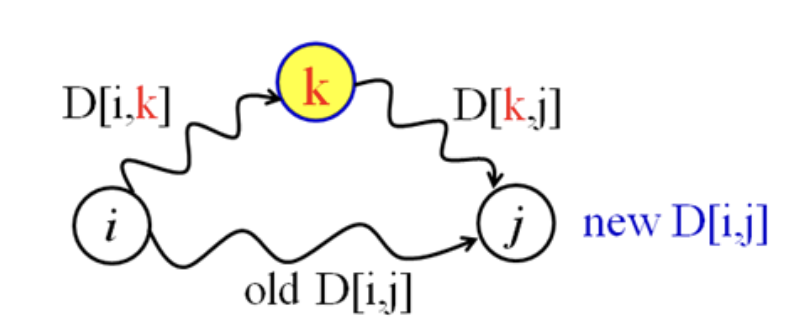
$D[i, j]$를 계산하기 위해서 미리 계산되어 있어야 할 부분 문제는 $D[i, k]$와 $D[k, j]$이다.

• Dijkstra는 Greedy를 기반하여, 현재 가장 비용이 적은 경로를 선택하며 진행하는데, 음수 간선이 있으면 최단 경로의 가중치가 더 작아지는 경로가 뒤늦게 발견될 수 있다.
• 방향성이 없는 그래프의 경우 음수 가중치는 블랙홀을 생성할 수 있다.
  • 해결: Bellman-Ford or constraint
• 반면에, Floyd는 경유하는 노드를 하나씩 늘려가면서 최단거리를 갱신하기 때문에 음수 간선이 있어도 갱신 과정에서 올바른 최단 경로를 찾는다.

5.1.4 Procedure

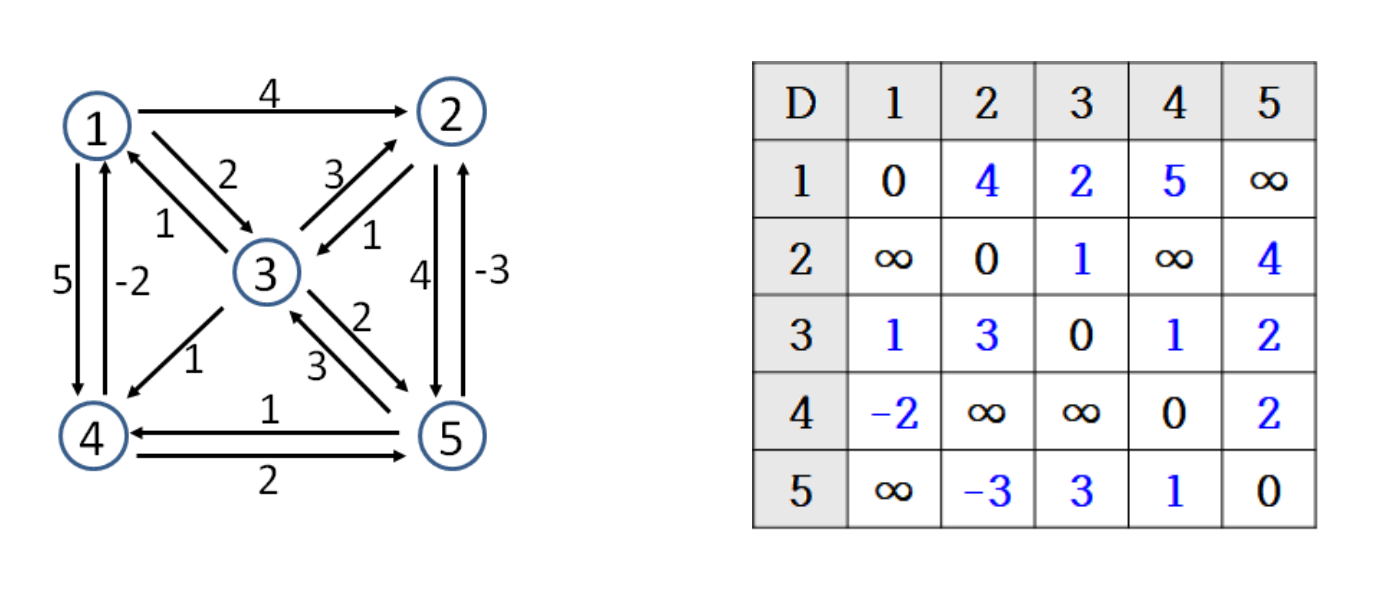
k=1일 때

1번 노드를 고려한 update이므로, i와 j가 1이 아닐 때를 고려한다.

• $D[4, 2] = min{D[4, 2], D[4, 1] + D[1, 2]} = min{\infin -2+4} = 2$

• $D[4, 3] = min{D[4, 3], D[4, 1] + D[1, 3]} = min{\infin -2+2} = 0$

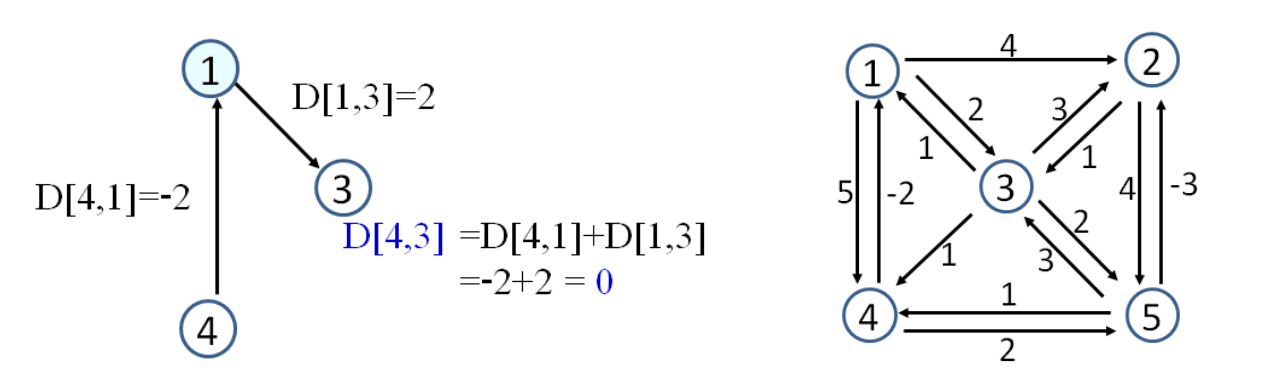
k=1일 때 수행 결과

• k=1일 때 $D[4, 2], D[4, 3]$이 각각 2,0으로 갱신, 다른 원소들은 변하지 않음

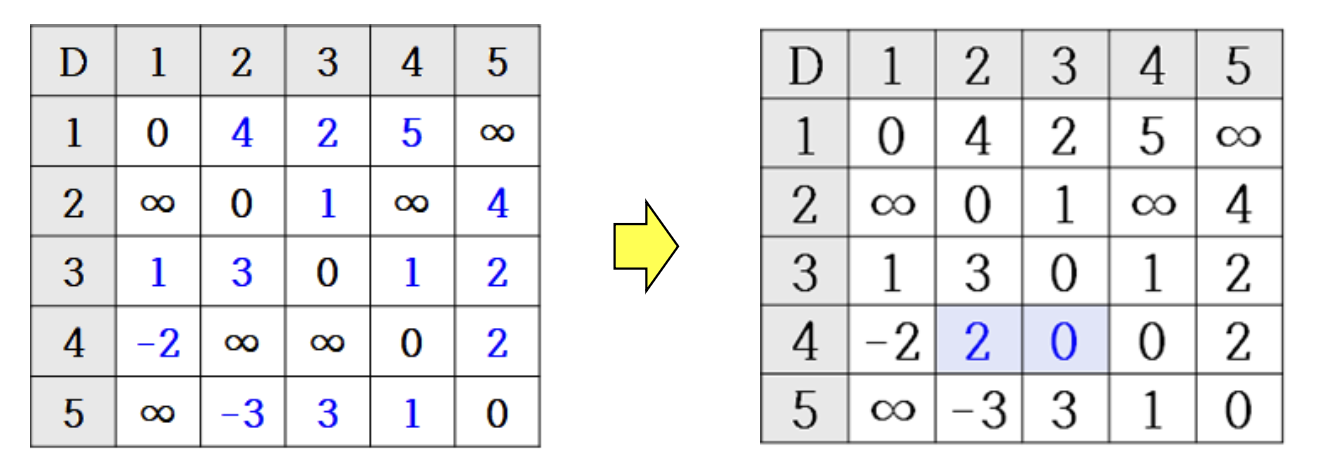
k=2일 때

• $D[1, 5]$가 $1 \rightarrow 2 \rightarrow 5$의 거리인 $8$로 갱신
• $D[5, 3]$이 $5 \rightarrow 2 \rightarrow 3$의 거리인 $-2$로 갱신

k=3일 때

• 총 7개의 원소 갱신

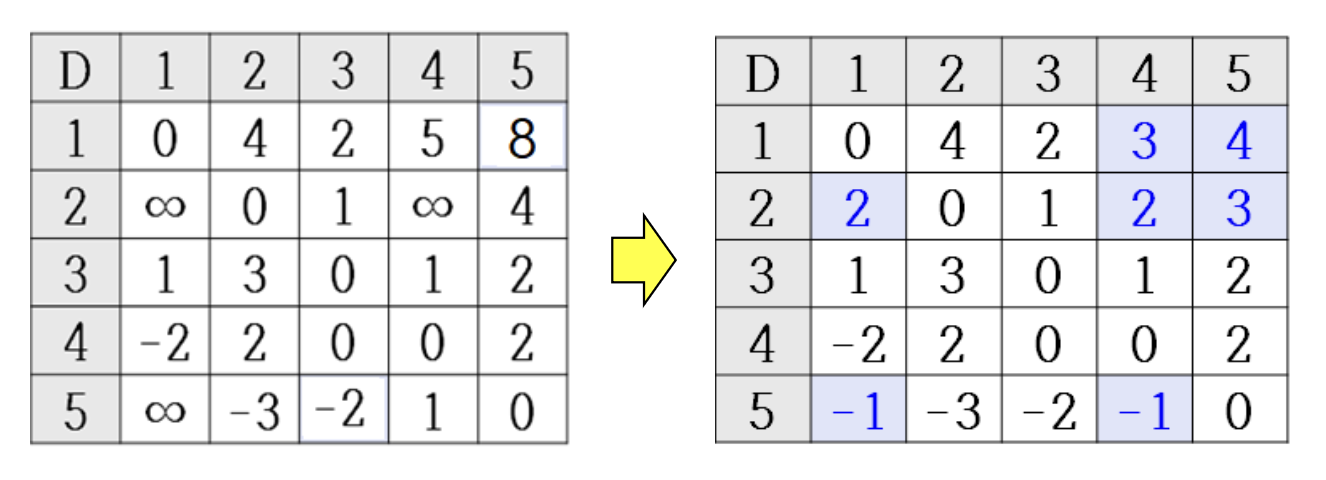
k=4일 때

• 총 3개의 원소가 갱신

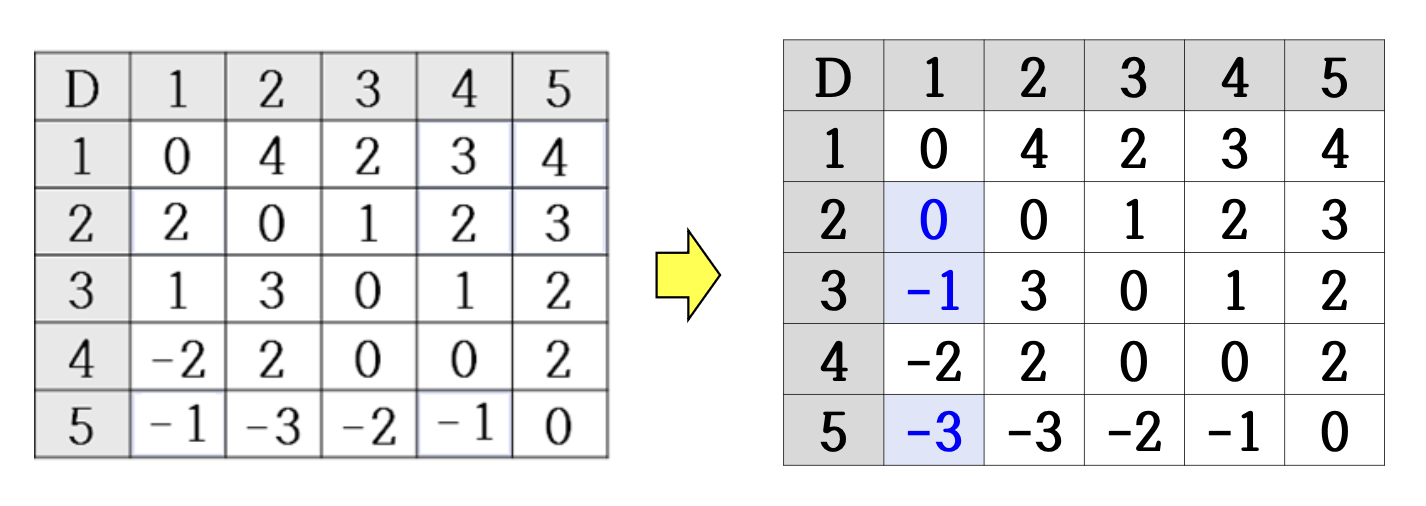
k=5일 때

• 총 3개의 원소가 갱신되고, 이것이 최종해가 된다.

5.1.5 Time Complexity

• 각 k에 대해서 모든 i, j 쌍에 대해 계산되므로, 총 $n \times n \times n = n^3$회 계산이 이루어지고, 각 계산은 $O(1)$ 시간 소요
• 시간 복잡도 $O(n^3)$

5.1.6 Application

• MapQuest, Google map
• Navigation
• GIS network analysis
• Communication Network
• Game
• VLSI Design

5.2 Chained Matrix Multiplications

• 연속된 행렬들의 곱셈에 필요한 원소 간의 최소 곱셈 횟수를 찾는 문제
• 10x20 행렬 $A$와 20x50 행렬 $B$를 곱하는데 원소 간의 곱셈 횟수는 10x20x5 = 1,000
• 두 행렬을 곱한 결과 행렬 $C$는 10x5

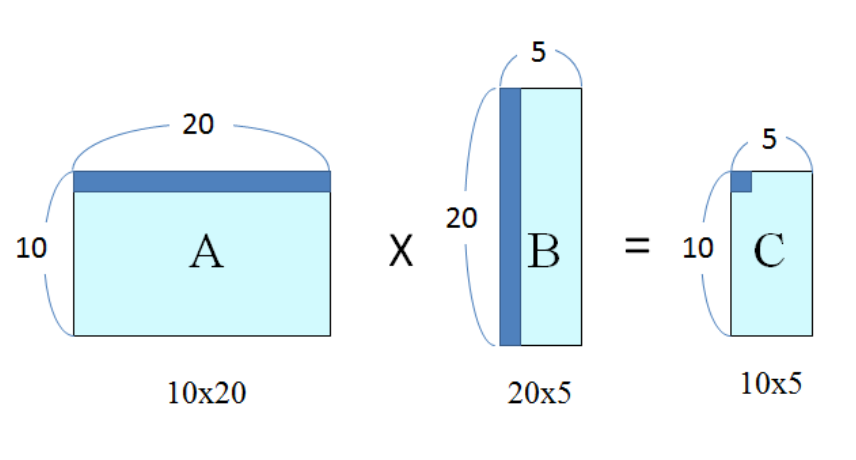
그림에서 C행렬의 해당 원소를 구하기 위해서 A의 1행, B의 1열 각각의 원소를 곱하고 전부 더하는 연산을 거쳐야 한다. 20번의 곱과 덧셈이 필요하다. 해당 원소 크기가 10x5개 존재하여 곱셈 횟수는 10x5x20이 된다.

5.2.1 Matrix Multiplications

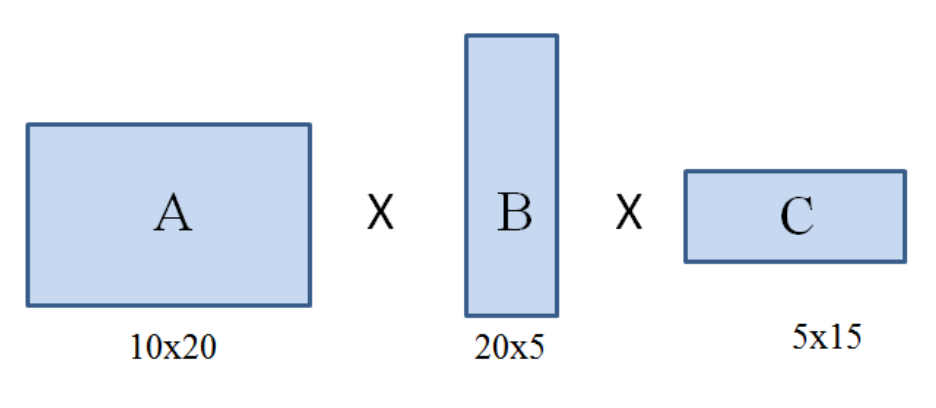
• 3개의 행렬을 곱해야 하는 경우
• 연속된 행렬의 곱셉에는 결합 법칙 허용
• AxBxC = (AxB)xC = Ax(BxC)

1. AxB를 계산한 후에 C를 곱하기

• AxB를 계산하는데 10x20x5 = 1,000번
• 결과 행렬의 크기가 10x5이고, 이에 행렬 C를 곱하면 10x5x15 = 750번
• 1,000 + 750 = 1,750회의 원소의 곱셈 필요

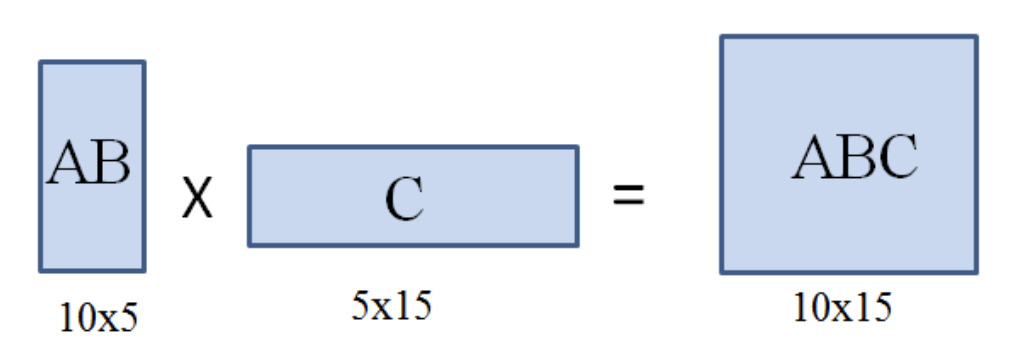
2. BxC를 계산한 후에 A를 곱하기

• BxC를 계산하는데 20x5x15 = 1,500번
• 그 결과 20x15 행렬이 만들어지고, 이를 행렬 A와 곱하면 10x20x15 = 3,000번
• 1,500 + 3,000 = 4,500회의 곱셈 필요

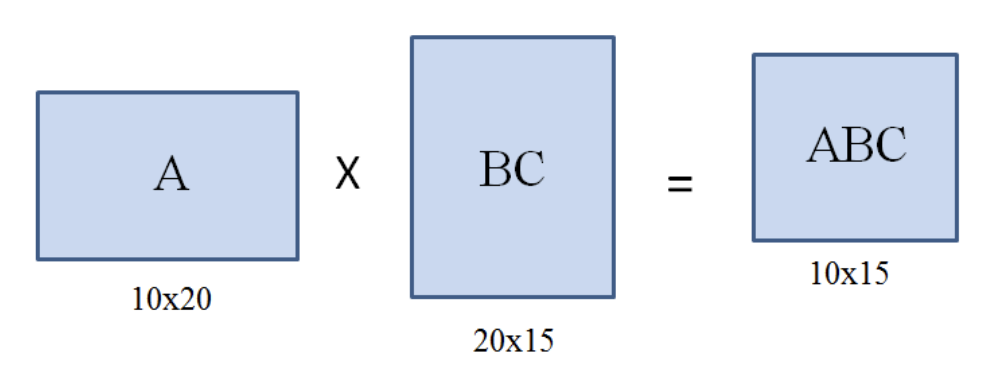
주어진 행렬의 순서를 잘 지켜서 반드시 이웃하는 행렬끼리 곱해야 한다.

5.2.2 SubProblem

ChainedMatrixMultiplications

• Input: 연속된 행렬 $A_1 \times A_2 \times ... \times A_n$
  • 단, $A_n$은 $d_{n-1} \times d_n$
• Output: 입력의 행렬 곱셈에 필요한 원소의 최소 곱셈 횟수

1. for $i = 1$ to $n$
2. $\,\,\,\,$ $C[i, j] = 0$
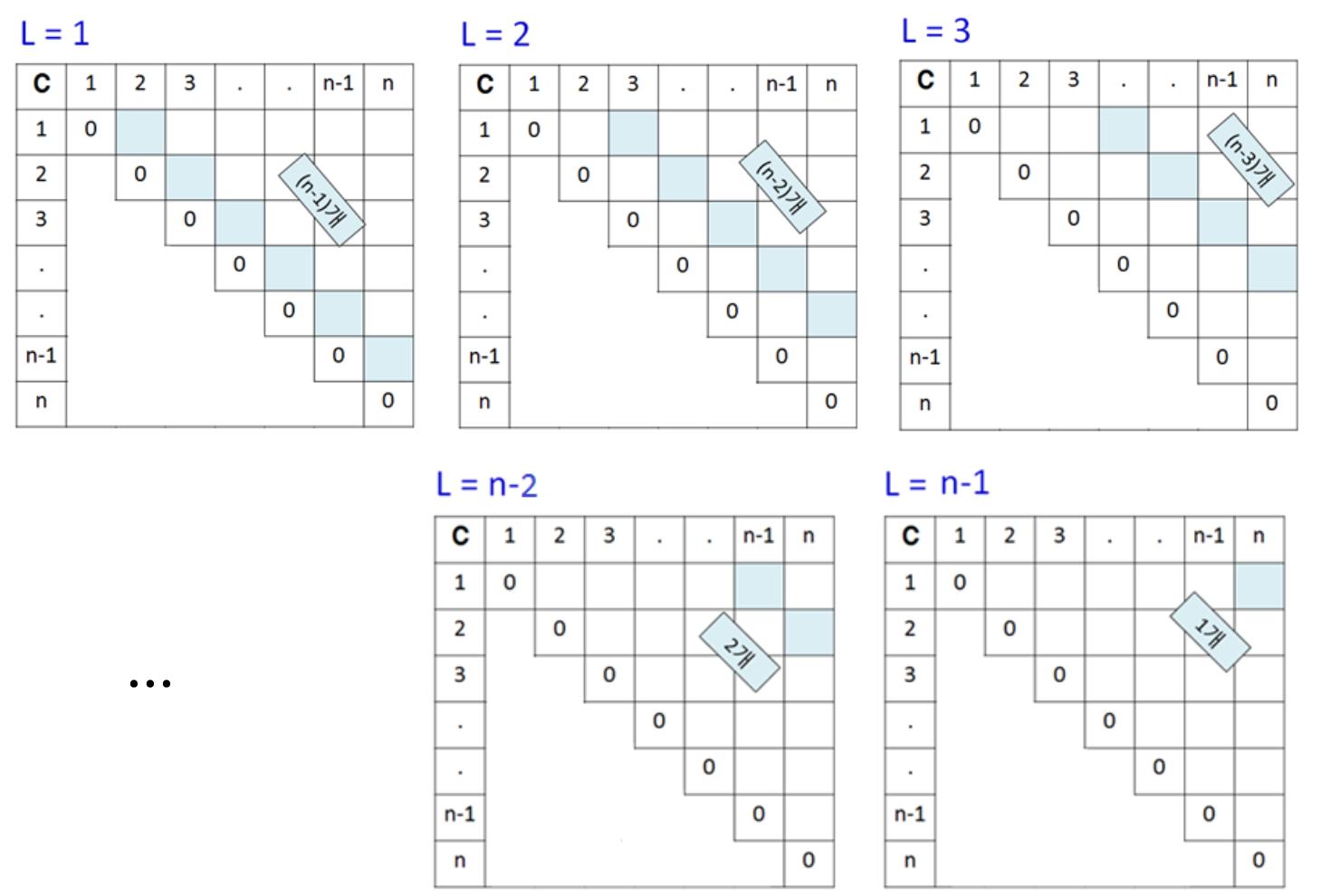
3. for $L = 1$ to $n-1$ $\,$ // L은 부분 문제의 크기를 조절하는 인덱스
4. $\,\,\,\,$ for $i = 1$ to $n-L$
5. $\,\,\,\,$$\,\,\,\,$ $j = i + L$
6. $\,\,\,\,$$\,\,\,\,$ $C[i, j] = \infin$ $\,$ // 초기화
7. $\,\,\,\,$$\,\,\,\,$ for $k=i$ to $j-1$
8. $\,\,\,\,$$\,\,\,\,$$\,\,\,\,$ temp $= C[i, k] + C[k+1, j] + d_{i-1} d_k d_j$
9. $\,\,\,\,$$\,\,\,\,$$\,\,\,\,$ if (temp $< C[i, j]$)
10. $\,\,\,\,$$\,\,\,\,$$\,\,\,\,$$\,\,\,\,$ $C[i, j]=$ temp
11. return $C[1, n]$

temp $= C[i, k] + C[k+1, j] + d_{i-1} d_k d_j$ 식이 의미하는 것은 왼쪽 연산 횟수 + 오른쪽 연산 횟수 + 새로운 행렬 연산 횟수이다.

Line3: for $L = 1$ to $n-1$

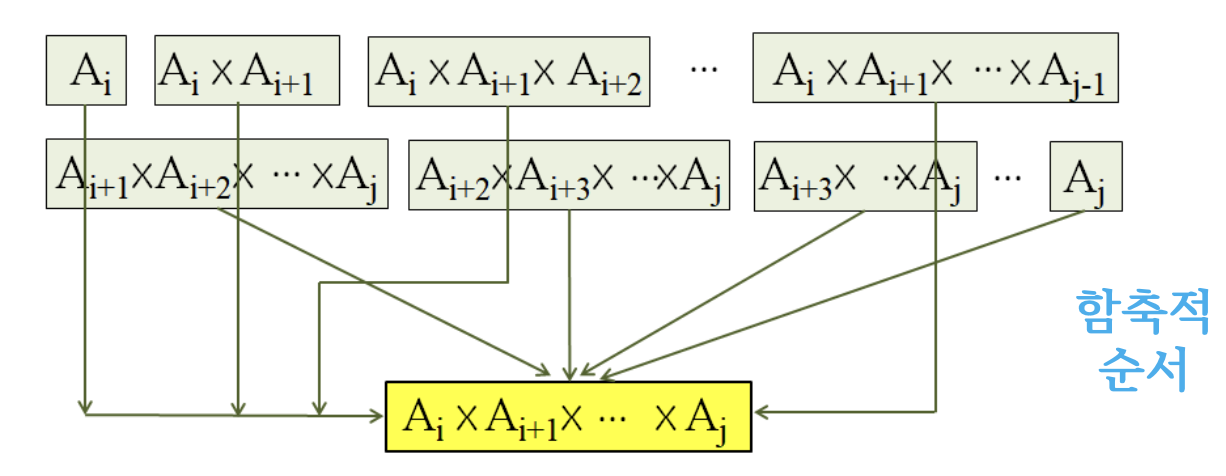
Line7: for $k=i$ to $j-1$

$\begin{aligned} &k=i \qquad (A_i) \times (A_{i+1}\times\cdots\times A_j)\\ &k=i+1 \qquad (A_i\times A_{i+1}) \times (A_{i+2}\times\cdots\times A_j)\\ &k=i+2 \qquad (A_i\times A_{i+1}\times A_{i+2}) \times (A_{i+3}\times\cdots\times A_j)\\ &\vdots\\ &k=j-1 \qquad (A_i\times\cdots\times A_{j-1}) \times (A_j) \end{aligned}$

5.2.3 Procedure

E.g. N = 4

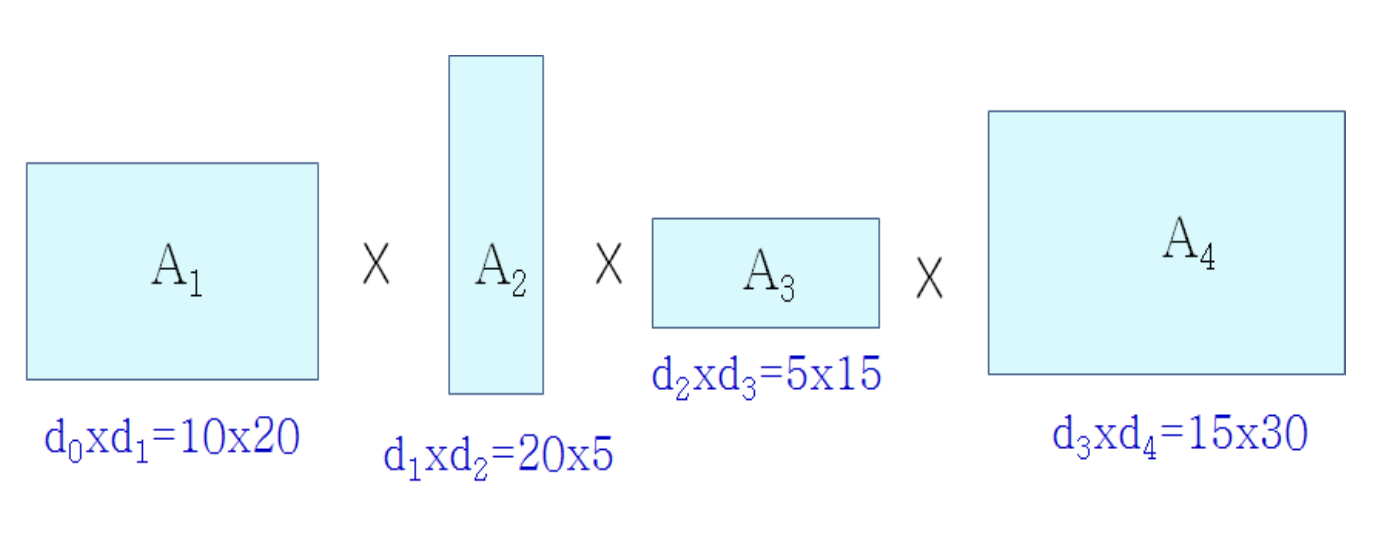
L=1일 때

두 개의 이웃한 행렬 곱셈만을 고려하는 단계

• $C[1,2]= d_0 d_1 d_2 = 10 \times 20 \times 5 = 1,000$
• $C[2,3]= 20 \times 5 \times 15 = 1,500$
• $C[3,4]= 5 \times 15 \times 30 = 2,250$

L=2, i=1일 때

$A_1 \times A_2 \times A_3$을 계산한다. $C[1,3]$

• k=1일 때
  • $A_1 \times (A_2 times A_3) =$ 4,500
• k=2일 때
  • $(A_1 \times A_2) times A_3 =$ 1,750

둘 중 더 작은 값 1,750 기록

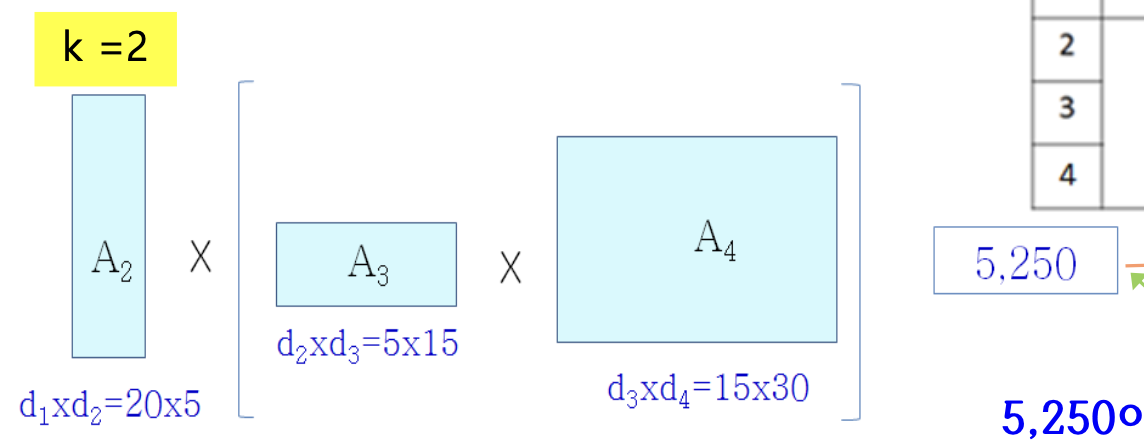
L=2, i=2일 때

$A_2 \times A_3 \times A_4$을 계산한다. $C[2,4]$

• k=2일 때

• k=3일 때

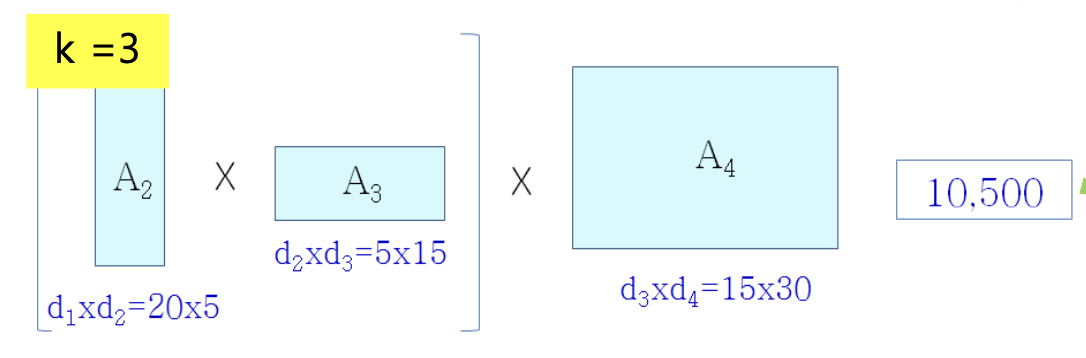
L=3일 때

$A_1 \times A_2 \times A_3 \times A_4$을 계산한다. $C[1,4]$

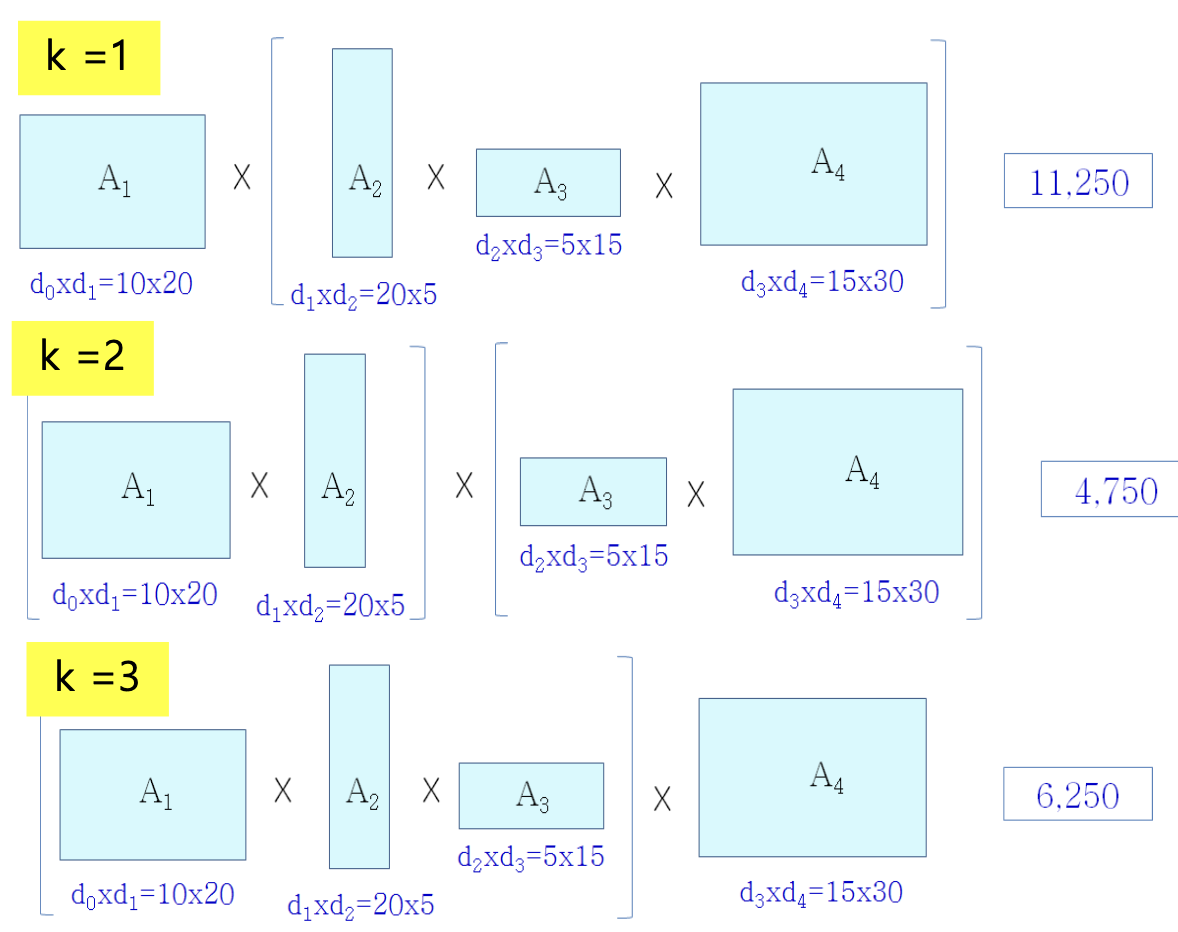
Result

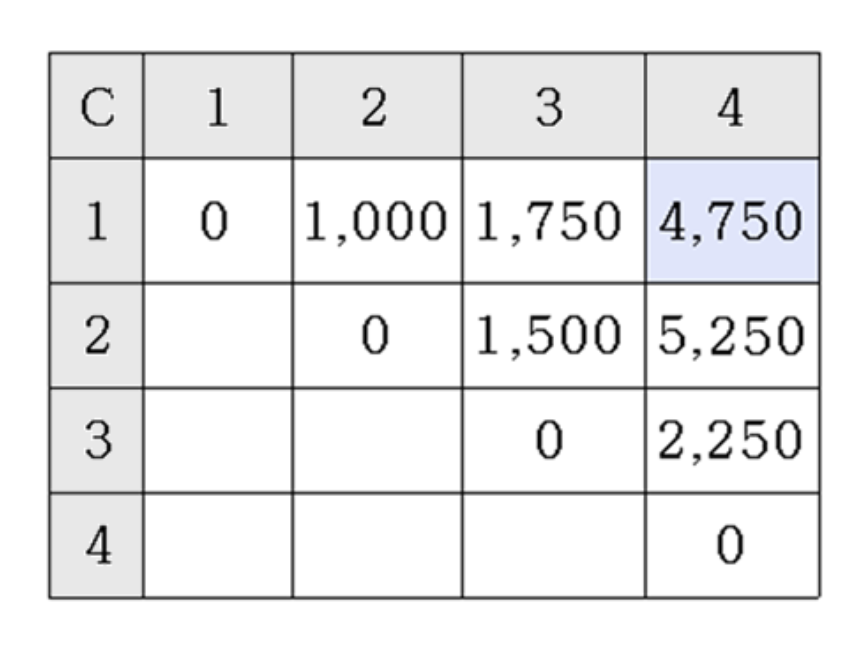
행렬 $n$개에 대하여, 부분 문제의 수는 $n(n-1)/2$가 된다.

5.2.4 Time Complexity

• 총 부분 문제 수
  • $(n-1) + (n-2) + ... + 2 + 1 = n(n-1)/2$
• 하나의 부분 문제는 k-loop가 최대 $(n-1)$번 수행
• Time Complexity: $O(n^2) \times O(n) = O(n^3)$