5. Dynamic Programming (2)

5.3 Edit Distance

삽입(insert), 삭제(delete), 대체(substitute) 연산을 사용하여 문자열 $S$를 수정하여 다른 문자열 $T$로 변환하고자 할 때 필요한 최소의 편집 연산 횟수

1. 'strong' $\rightarrow$ 'stone'

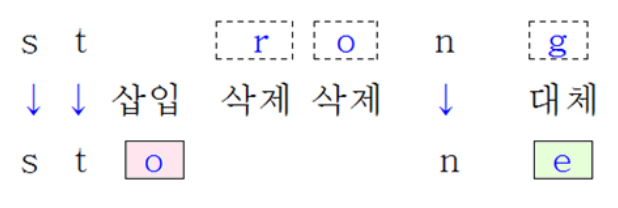
• 위에서는 's'와 't'는 그대로 사용하고, 'o'를 삽입하고, 'r'과 'o'를 각각 삭제
• 그리고 'n'을 그대로 사용하고, 마지막으로 'g'를 'e'로 대체하여, 총 4회의 편집 연산 수행

없는 글자 삭제는 필수, 대체는 삭제 + 삽입보다 비용이 저렴하다.

2. 'strong' $\rightarrow$ 'stone'

• 's'와 't'는 그대로 사용한 후, 'r'을 삭제하고, 'o'와 'n'을 그대로 사용한 후, 'g'를 'e'로 대체하여, 총 2회의 편집 연산만이 수행되고, 이는 최소 편집 횟수이다.

$S$를 $T$로 바꾸는데 어떤 연산을 어느 문자에 수행하는가에 따라서 편집 연산 횟수가 달라진다.

5.3.1 Subproblem Definition

Prefix

• 'strong' $\rightarrow$ 'stone'
• stro를 sto로 바꾸는 편집 거리를 미리 알면, ng를 ne로 바꾸는 편집 거리를 찾음으로써 주어진 입력에 대한 편집 거리를 구할 수 있다.

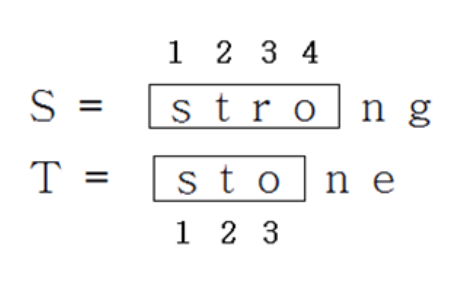
편집 거리 알고리즘은 "부분 문제"를 점화식으로 쪼개서 푸는데 두 문자열의 각각 모든 접두부 조합에 대해 "최소 편집 거리"를 미리 구해 놓으면 전체를 쉽게 해결할 수 있다.

Subproblem Definition

$|S| = m, \quad |T| = n$

$S = s_1 \; s_2 \; s_3 \; s_4 \; \cdots \; s_m$

$T = t_1 \; t_2 \; t_3 \; t_4 \; \cdots \; t_n$

• $E[i, j]=$ $S$의 처음 i개 문자를 $T$의 처음 j개 문자로 바꾸는데 필요한 편집 거리
• 'strong' $\rightarrow$ 'stone'에 대해서, stro를 sto로 바꾸기 위한 편집 거리는 $E[4, 3]$이다.

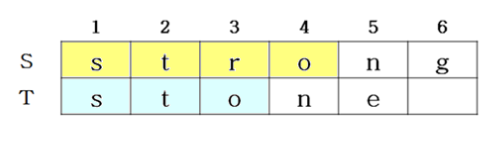
최대로 중복되는 문자(substring)를 찾는 것이 편집 거리 문제이다.
E[6, 5]는 E[4, 3], 즉 substring에서부터 파생된다.

5.3.2 'strong' $\rightarrow$ 'stone'에 대해

$s_1 \rightarrow t_1$

• ['s' $\rightarrow$ 's']
• $s_1 = t_1 =$ 's'이므로 $E[1,1] = 0$

$s_1 \rightarrow t_1t_2$

• ['s' $\rightarrow$ 'st']
• $s_1 = t_1=$'s'이고, 't'를 삽입하므로 $E[1,2] = 1$

$s_1s_2 \rightarrow t_1$

• ['st' $\rightarrow$ 's']
• $s_1 = t_1=$'s'이고, 't'를 삭제하여 $E[2,1] = 1$

$s_1s_2 \rightarrow t_1t_2$

• ['st' $\rightarrow$ 'st']
• $s_1 = t_1=$'s'이고, $s_2 = t_2=$'t'이므로 $E[2,2] = 0$
• 이 경우에는 $E[1,1] = 0$이라는 결과를 이용하고, $s_2 = t_2=$'t'이므로, $E[2,2] = E[1,1] + 0 = 0$

5.3.3 E[i, j]

E[4,3] 계산 방법

• $s_1s_2s_3s_4 \rightarrow t_1t_2$

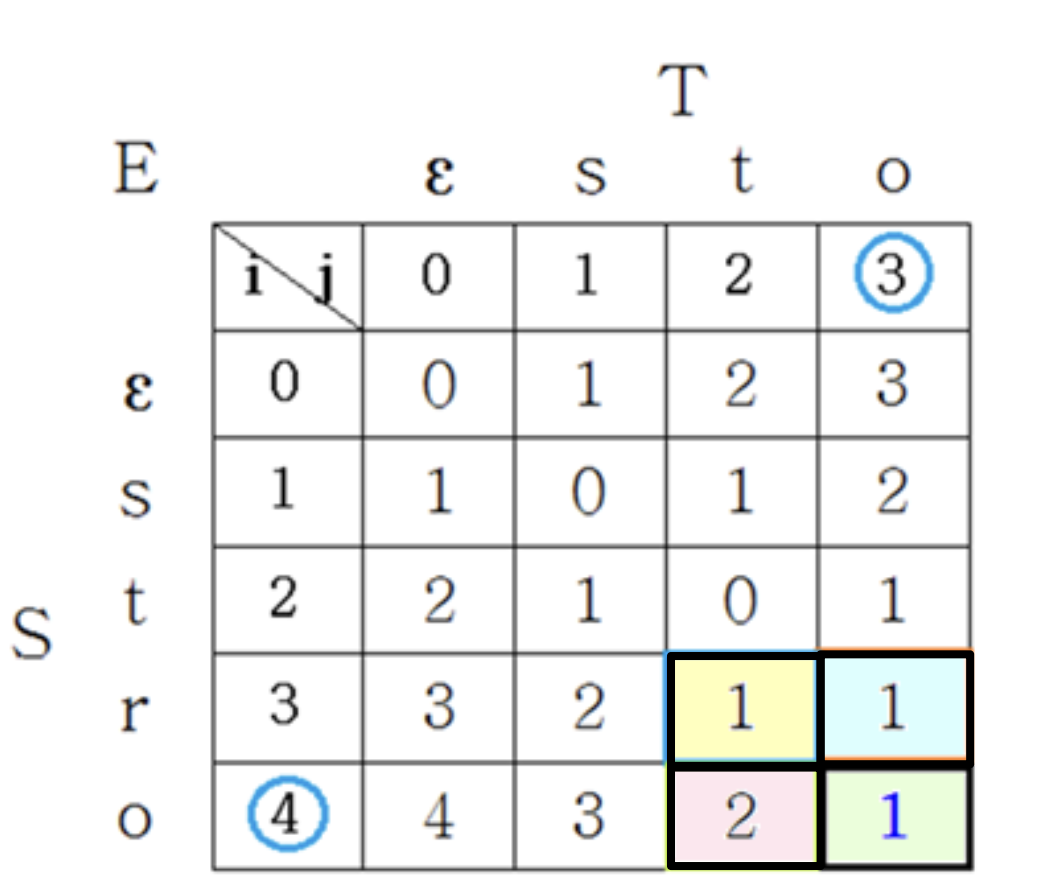
1. E[4, 2]의 해를 알면, $t_3 =$ 'o'를 삽입하면 E[4, 2] + 1
2. E[3, 3]의 해를 알면, $s_4 =$ 'o'를 삭제하면 E[3, 3] + 1
3. E[3, 2]의 해를 알면, $s_4 =$ 'o'과 $t_3 =$ 'o'이 같으므로 E[3, 2] + 0

Generalization: E[i, j]

$E[i, j] = \min\left\{ E[i, j-1] + 1, E[i-1, j] + 1,\; E[i-1, j-1] + \alpha \right\}$

$\text{단},\; \alpha = \begin{cases} 1 & \text{if } s_i \neq t_j \\ 0 & \text{if } s_i = t_j \end{cases}$

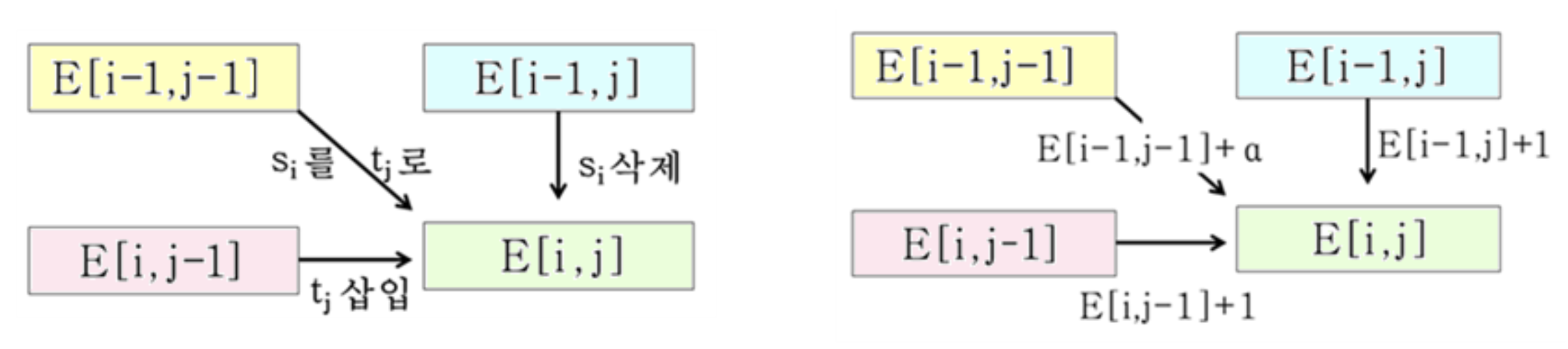
Initialization

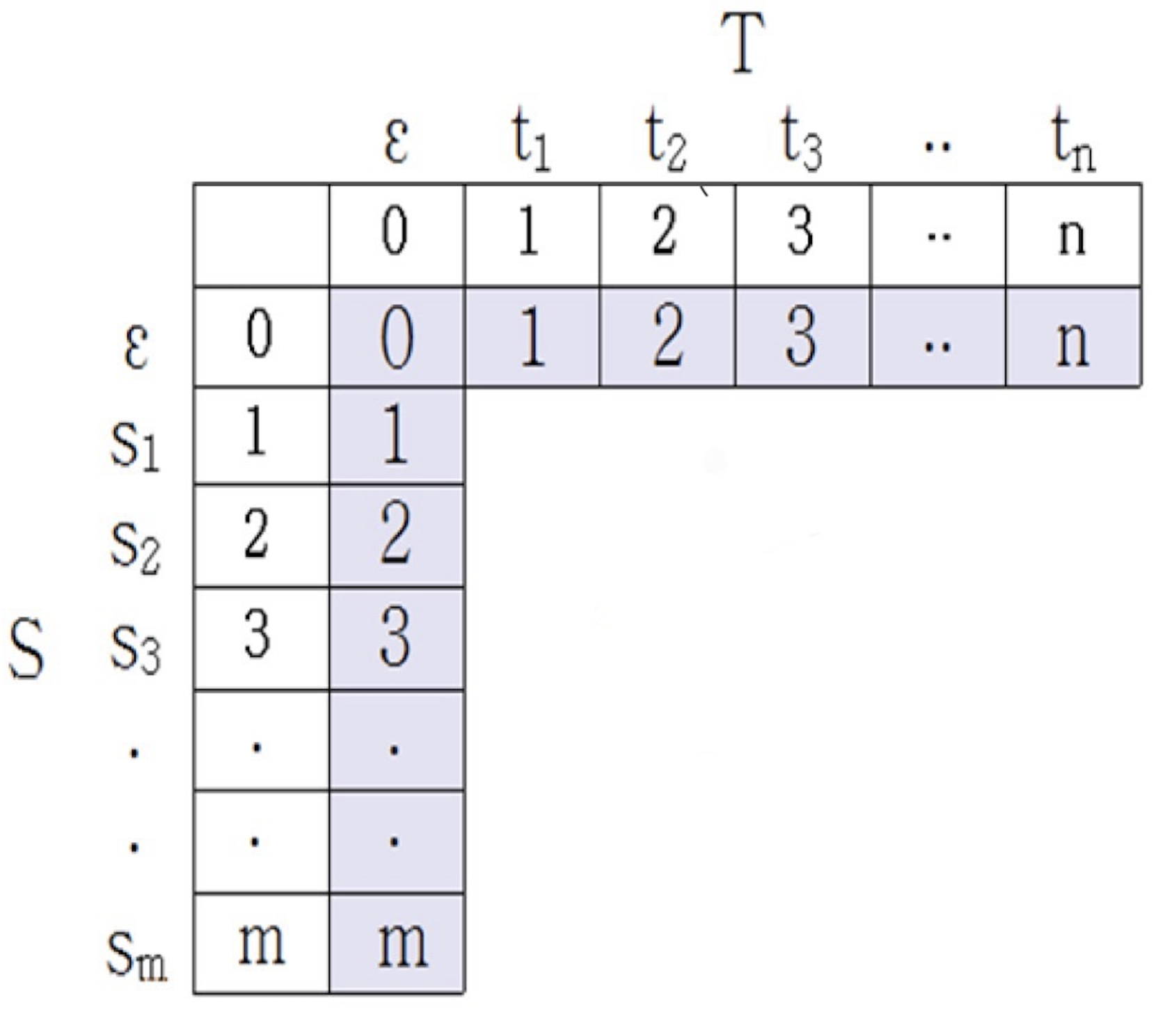
• 0번 행의 0 ~ n 초기화 의미
  • $S$의 첫 문자를 처리하기 전에 즉, $S$가 $\epsilon$(공 문자열)인 상태에서 $T$의 문자를 좌에서 우로 하나씩 만들어 가는데 필요한 삽입 연산 횟수를 각각 나타낸다.
• 0번 열의 0 ~ m 초기화 의미
  • $T$를 $\epsilon$로 만들기 위해서, $S$의 문자를 위에서 아래로 하나씩 없애는데 필요한 삭제 연산 횟수를 각각 나타낸다.

EditDistance

• Input: $S$, $T$(각 문자열의 길이는 각각 m과 n이다.)
• Output: $S$를 $T$로 변환하는 편집 거리, $E[m,n]$

1. for i=0 to m; E[i,0] = i // 0번 열 초기화
2. for j=0 to n; E[0,j] = j // 0번 행 초기화
3. $\,\,\,\,$ for i=1 to m // 각 행에 대해서
4. $\,\,\,\,$$\,\,\,\,$ for j=1 to n // 각 열에 대해서
5. $\,\,\,\,$$\,\,\,\,$$\,\,\,\,$ E[i, j] = min{E[i, j-1] + 1, E[i-1, j] + 1, E[i-1, j-1] + $\alpha$}
6. return E[m, n]

5.3.4 Procedure

'strong' $\rightarrow$ 'stone'의 편집 거리

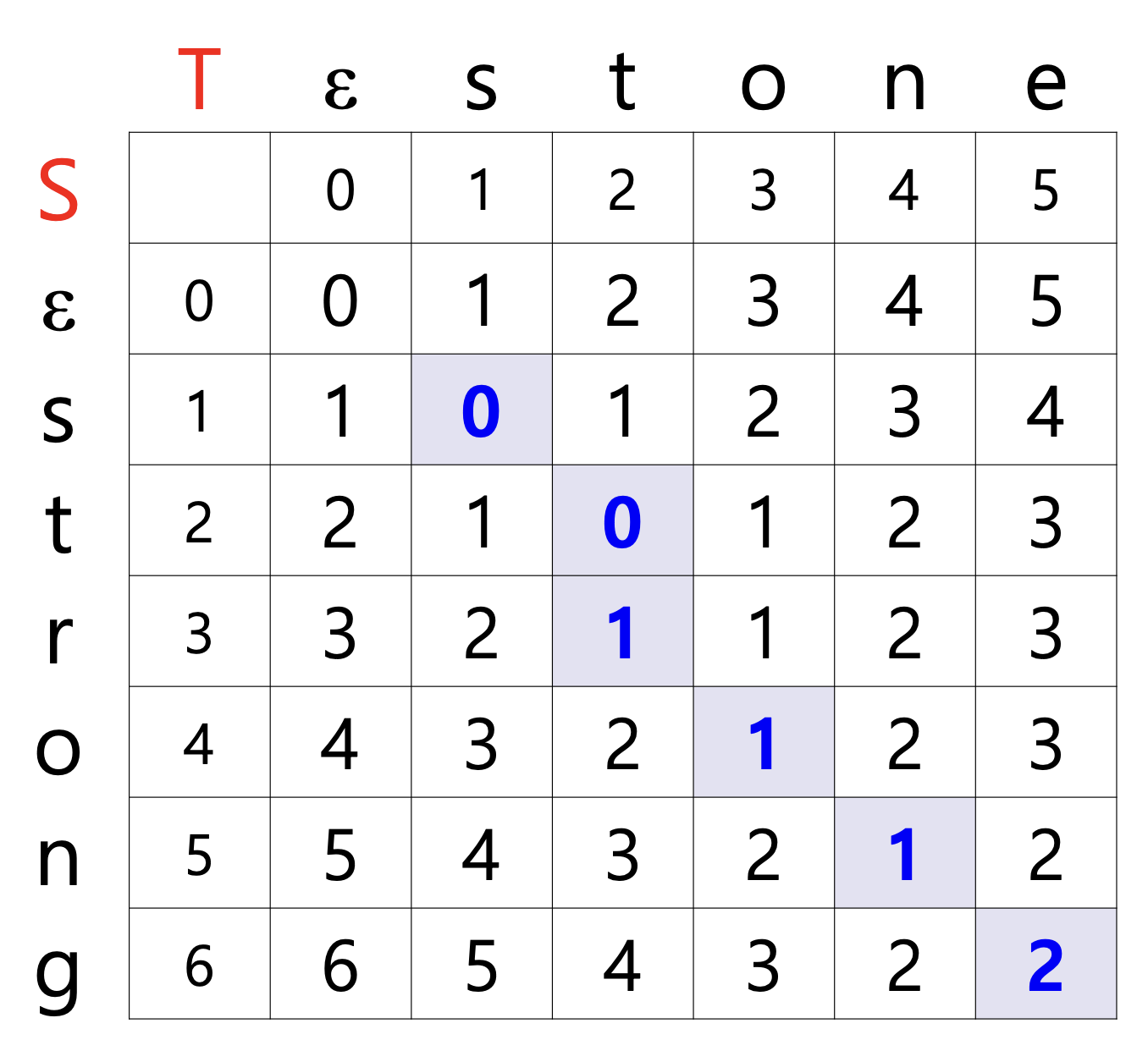
E[1, 1]

• E[1, 1] = min{E[1, 0] + 1, E[0, 1] + 1, E[0, 0] + $\alpha$}
• S와 T가 같은 경우에는 $\alpha$가 0이다.

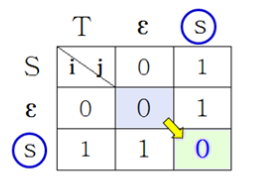
E[2, 2]

• E[2, 2] = min{E[2, 1] + 1, E[1, 2] + 1, E[1, 1] + $\alpha$}

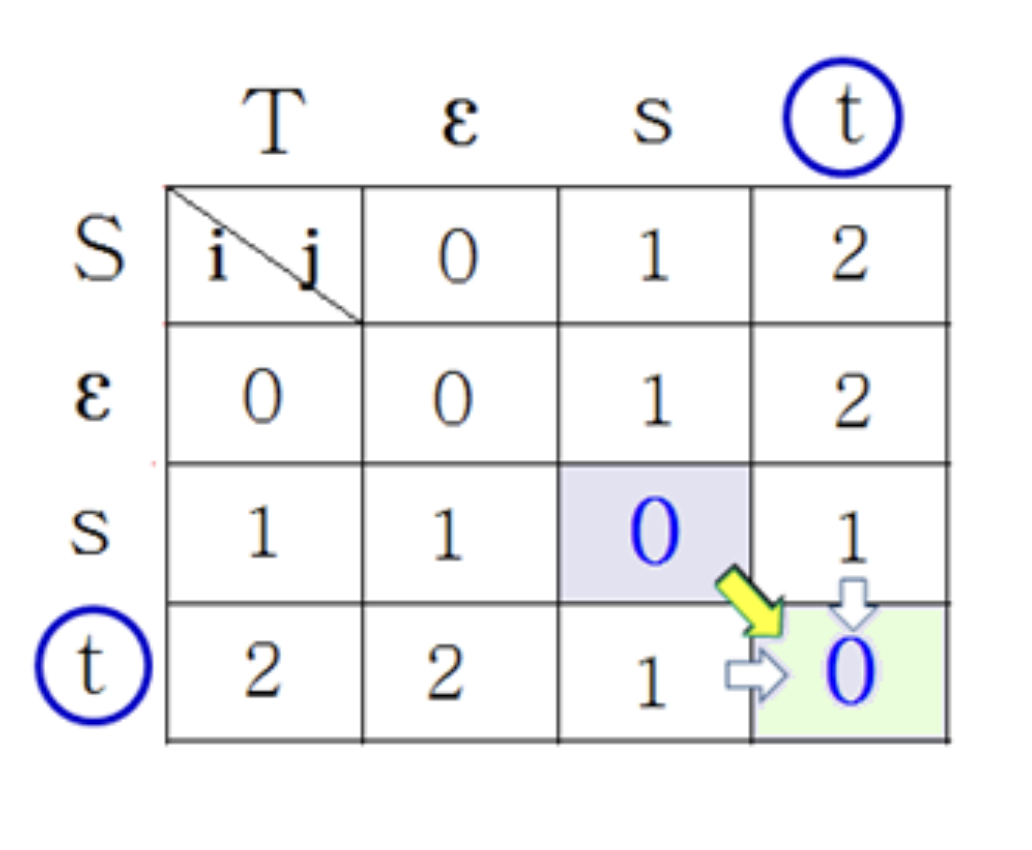
E[3, 2]

• E[3, 2] = min{E[3, 1] + 1, E[2, 3] + 1, E[2, 2] + $\alpha$}

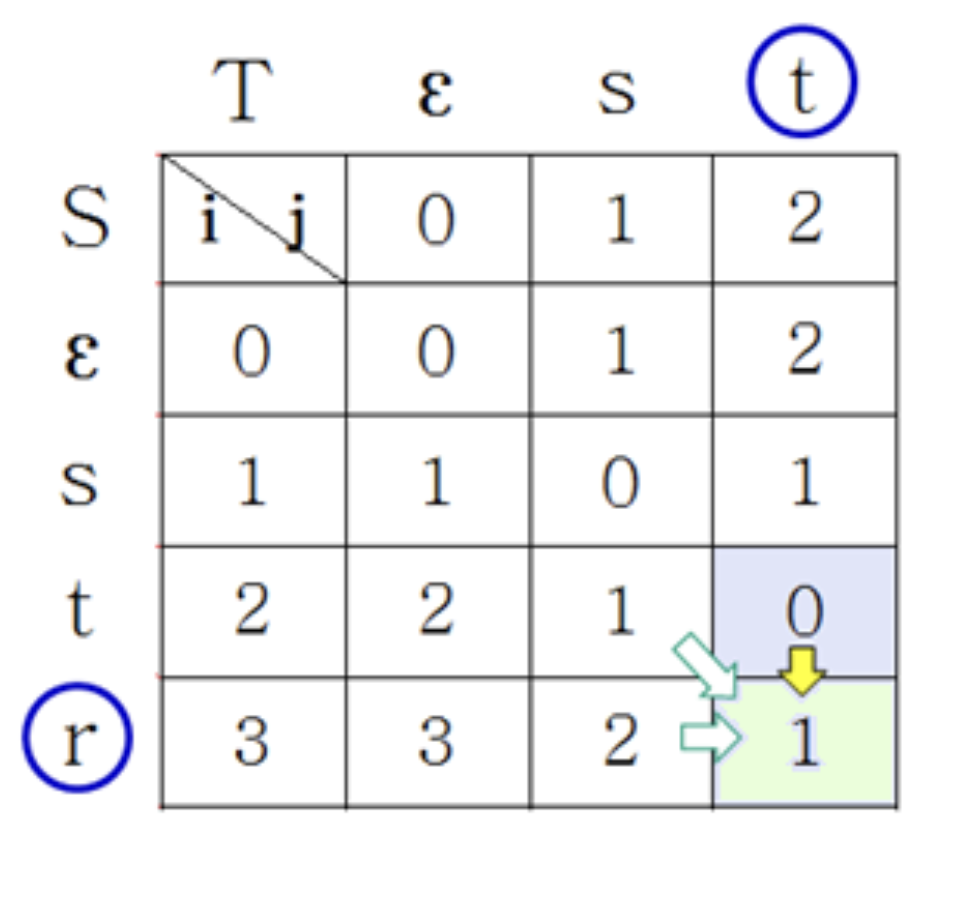
E[4, 3]

• E[4, 3] = min{E[4, 2] + 1, E[3, 3] + 1, E[3, 2] + $\alpha$}

E[5, 4]

• E[5, 4] = min{E[5, 3] + 1, E[4, 4] + 1, E[4, 3] + $\alpha$}

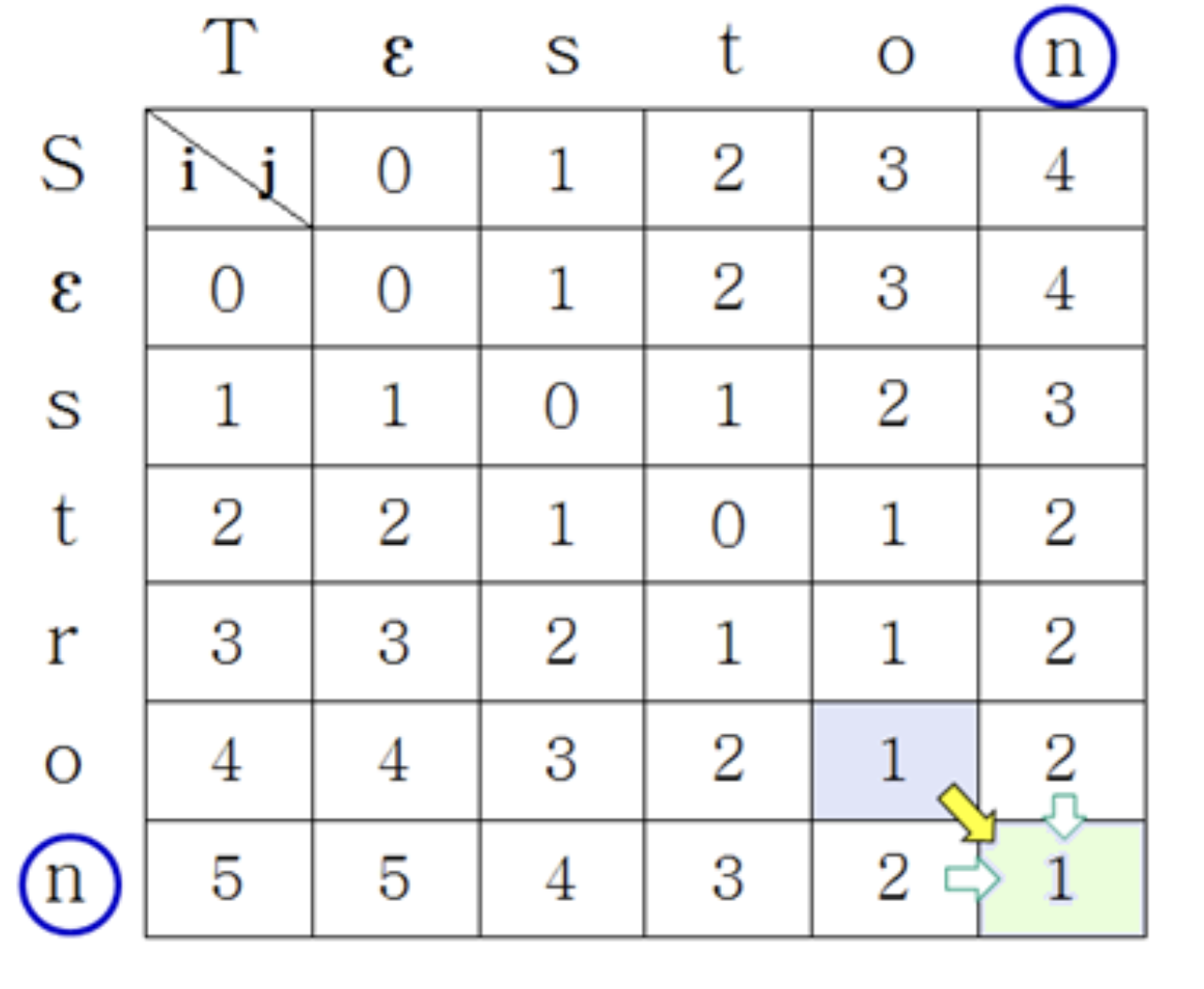
E[6, 5]

• E[6, 5] = min{E[6, 4] + 1, E[5, 5] + 1, E[5, 4] + $\alpha$}

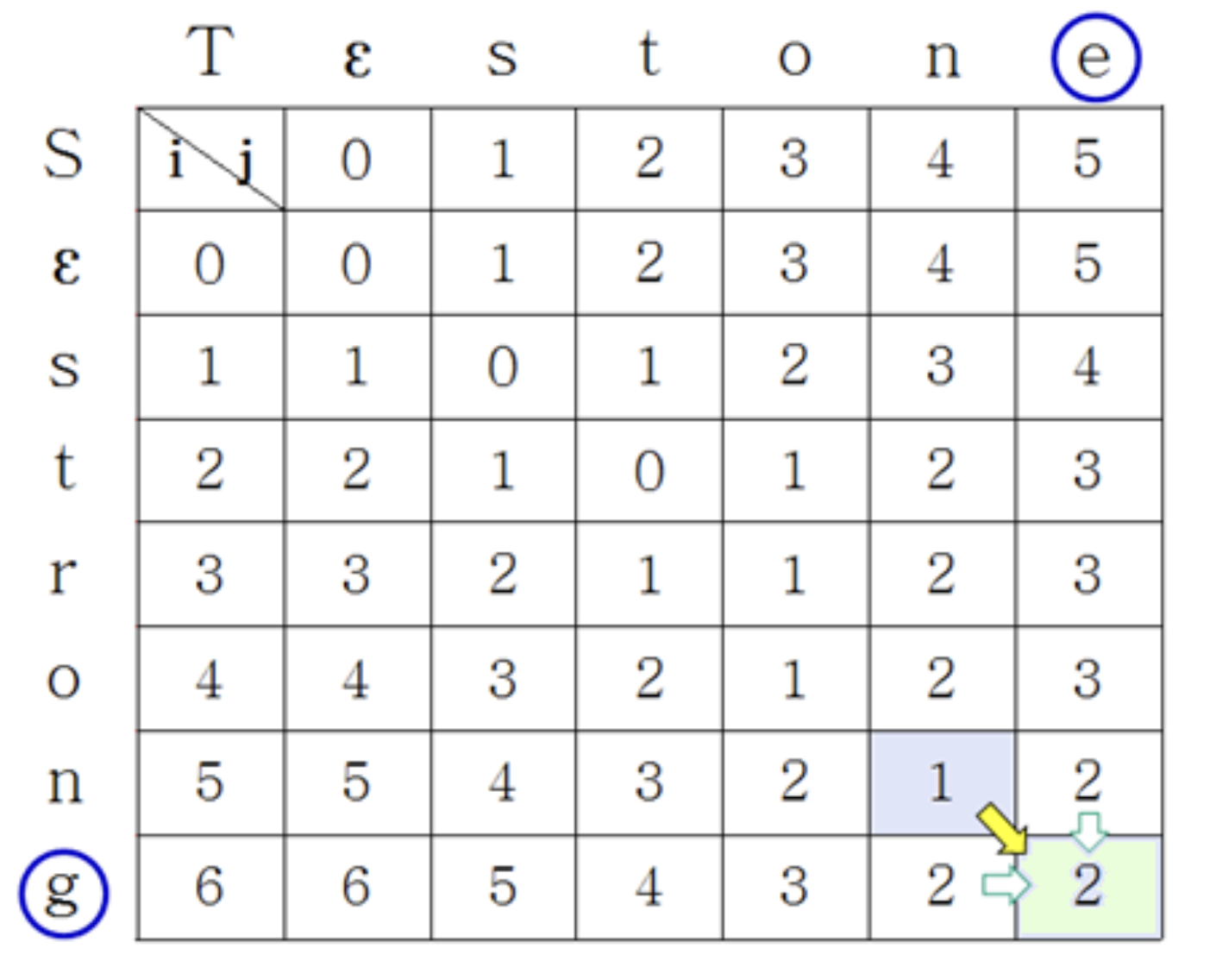
5.3.5 Time Complexity

• 시간 복잡도는 $O(mn)$
  • 단, m과 n은 두 문자열 각각의 길이
• 총 부분 문제의 수가 배열 E의 원소 수인 mxn이고, 각 부분 문제를 계산하기 위해 주위의 3개의 부분 문제들의 해를 참조한 후, 최솟값을 찾는 것이므로 $O(1)$ 시간 소요

5.3.6 Application

• 생물 정보 공학 및 의학 분야
  • 편집 거리가 작으면 문자열들이 서로 유사하다고 판단할 수 있으므로 두 개의 유전자가 얼마나 유사한가 측정하는데 활용
  • 환자의 유전자 속에서 암 유전자와 유사한 유전자를 찾아 미리 진단
  • 암세포에만 있는 특징을 분석하여 항암제 개발
  • 좋은 형질을 가진 유전자들 탐색
• 철자 오류 검색
• 광학 문자 인식에서의 보정 시스템
• 자연어 번역