5. Dynamic Programming (3)

5.4 Knapsack

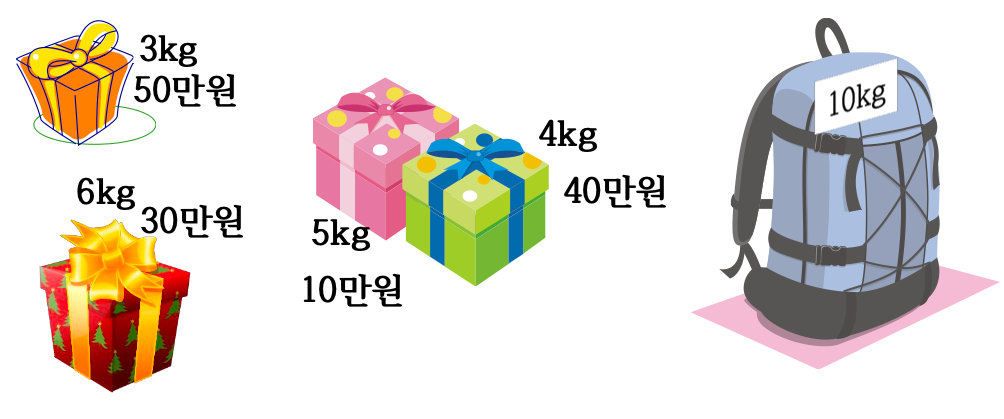
• $n$개의 물건과 각 물건 $i$의 무게 $w_i$와 가치 $v_i$가 주어지고 배낭의 용량이 $C$일 때, 배낭에 담을 수 있는 물건의 최대 가치는?
• 단, 배낭에 담은 물건의 무게의 합이 $C$를 초과하지 말아야 하고, 각 물건은 1개씩만 있다.
• 이러한 배낭 문제를 0-1 배낭 문제라고 한다.

5.4.1 Subproblem

• 물건
• 물건의 무게
• 물건의 가치
• 배낭의 용량

4가지 요소가 존재하는데, 물건과 물건의 무게는 부분 문제를 정의하는데 필요하다.

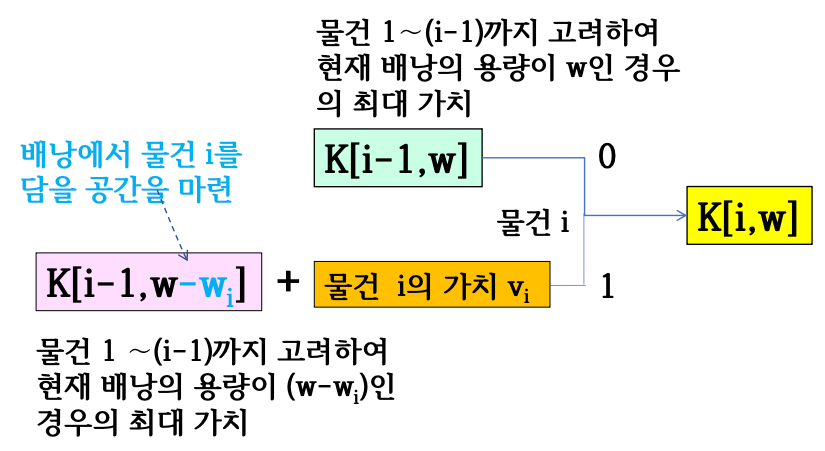
• $K[i, w] =$ 물건 $1$ ~ $i$까지만 고려하고, (임시) 배낭의 용량이 $w$일 때의 최대 가치
• 단 $i = 1, 2, ... , n$이고, $w = 1, 2, 3, ... , C$
• 문제의 최적해 = $K[n, C]$

Knapsack

• Input: 배낭의 용량 $C$, $n$개의 물건과 각 물건 $i$의 무게 $w_i$와 가치 $v_i$, 단 $i = 1, 2, ... , n$
• Output: $K[n, C]$

1. for i = 0 to n $\,\,$ K[i, 0] = 0 // 배낭의 용량이 0일 때
2. for w = 0 to C $\,\,$ k[0, w] = 0 // 물건 0이란 어떤 물건도 고려하지 않을 때
3. for i = 1 to n // 각 행에 대해서
4. $\,\,\,\,$ for w = 1 to C // w는 배낭의 (임시) 용량)
5. $\,\,\,\,$ $\,\,\,\,$ if ($w_i$ > w) // 물건 i의 무게가 임시 배낭 용량을 초과하면
6. $\,\,\,\,$ $\,\,\,\,$ $\,\,\,\,$ K[i, w] = K[i-1, w]
7. $\,\,\,\,$ $\,\,\,\,$ else
8. $\,\,\,\,$ $\,\,\,\,$ $\,\,\,\,$ K[i, w] = max{K[i-1, w], K[i-1, w- $w_i$] + $v_i$}
9. return K[n, C]

5.4.2 Procedure

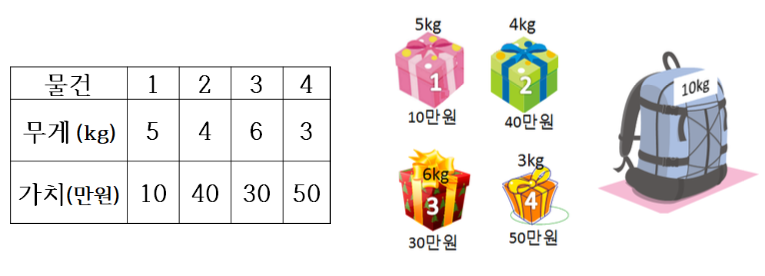
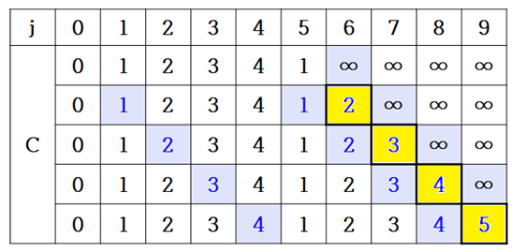
• 배낭의 용량 C = 10kg

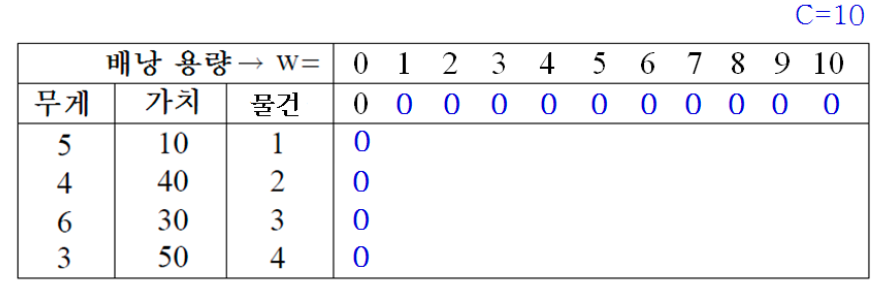
Line1~2

• 0번 행과 0번 열의 각 원소를 0으로 초기화

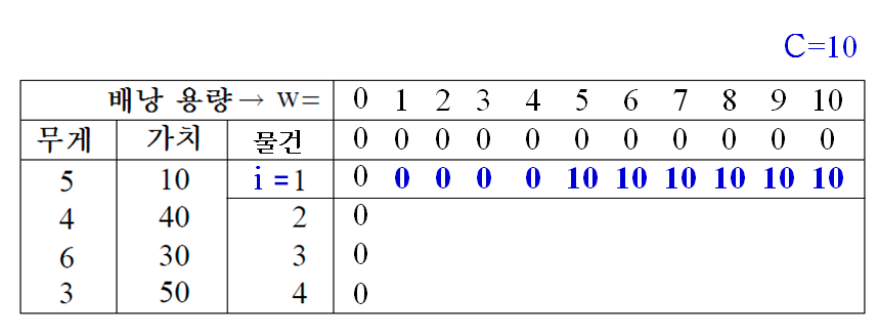
물건 1(5kg)만 고려

• w = 1, 2, 3, 4일 때, 각각 물건 1을 담을 수 없다.
  • K[1, 1] = 0, K[1, 2] = 0, K[1, 3] = 0, K[1, 4] = 0

• w = 5(배낭의 용량 5kg)일 때
  • K[1, 5] = 10

• w = 6, 7, 8, 9, 10일 때
  • K[1, 6] = K[1, 7] = K[1, 8] = K[1, 9] = K[1, 10]

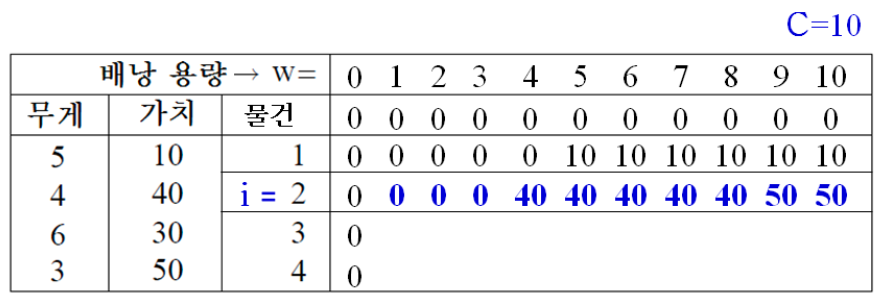
물건 2(4kg)

• w = 1, 2, 3일 때
  • K[2, 1] = 0, K[2, 2] = 0, K[2, 3] = 0
• w = 4일 때
  • K[2, 4] = 40
• w = 5일 때
  • K[2, 5] = max{K[i-1, w], K[i-1, w- $w_i$] + $v_i$}
    = max{K[2-1, 5], K[2-1, 5-4] + 40}
    = max{10, 0+40}
    = max{10, 40} = 40
  • 물건 1을 배낭에서 뺀 후, 물건 2를 담는다. 그때의 가치가 40이다.
• w = 6, 7, 8일 때
  • 각각의 경우도 물건 1을 빼내고 물건 2를 담는 게 더 큰 가치를 얻는다.
  • K[2, 6] = K[2, 7] = K[2, 8] = 40
• w = 9일 때
  • K[2, 9] = max{K[i-1, w], K[i-1, w- $w_i$] + $v_i$}
    = max{K[2-1, 9], K[2-1, 9-4] + 40}
    = max{10, 10+40}
    = max{10, 50} = 50
  • 물건 1과 2를 둘 다 담을 수 있다.
• w = 10일 때
  • 물건 1과 2 둘 다 담을 수 있다.

5.4.3 Result

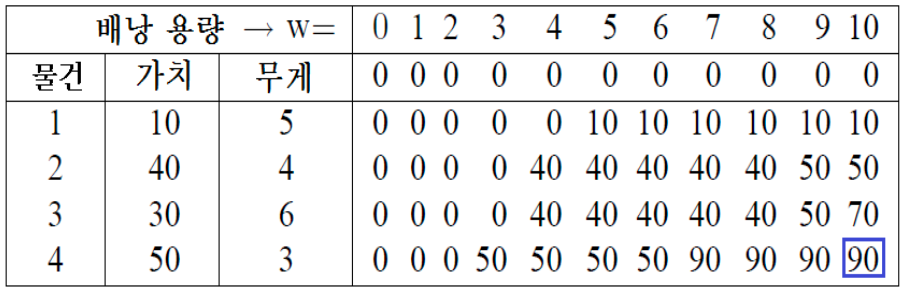
최적해는 K[4, 10]= 90이 된다.

K[i-1, w- $w_i$]: i번째 물건을 넣었을 때 남는 용량에서 최적값, 여기에 이번 물건의 가치 $v_i$를 더한다.

5.4.4 Time Complexity

1개의 부분 문제의 해를 구할 때

• Line5에서의 무게를 1번 비교한 후, Line6에서는 1개의 부분 문제의 해를 참조하고, Line8에서는 2개의 해를 참조한 계산이므로 $O(1)$ 시간

부분 문제 수

• 배열 K의 원소 수인 $n \times C$
• $C$ = 배낭의 용량

Knapsack's Time Complexity

• $O(1) \times n \times C = O(nC)$

5.4.5 Application

배낭 문제는 다양한 분야에서 의사 결정 과정에 활용

• 원자재의 버리는 부분을 최소화 시키기 위한 자르기/분할
• 금융 포트폴리오와 자산 투자의 선택
• 암호 생성 시스템 (Merkle-Hellman Knapsack Cryptosystem)

5.5 Coin Change

대부분의 경우 그리디 알고리즘으로 해결되나, 해결 못하는 경우도 있다. DP 알고리즘은 모든 동전 거스름돈에 대해 항상 최적해를 찾는다.

5.5.1 Subproblem

• 문제에 주어진 요소들
  • 동전의 종류 $d_1, d_2, ... , d_k$, 단 $d_1 > d_2 > ... > d_k = 1$
  • 거스름돈 $n$원

배낭 문제의 DP 알고리즘은 배낭의 용량을 1kg씩 증가시켜가며 문제를 해결한다.

• 1원씩 증가시켜가며 문제를 해결하자.
• 거스름돈을 배낭의 용량과 같이 생각하자.

1차원 배열 $C$

• C[1] = 1원을 거슬러 받을 때 사용되는 최소의 동전 수
• C[2] = 2원을 거슬러 받을 때 사용되는 최소의 동전 수
  ...
• C[n] = n원을 거슬러 받을 때 사용되는 최소의 동전 수

C[j]를 계산하는데 어떤 부분 문제가 필요한가?

• 500원 동전이 필요하면 j-500원의 해, C[j-500]에다가 500원 1개 추가
  ...
• 1원 동전이 필요하면 j-1원의 해, C[j-1]에다가 1원 동전 추가

$\,\,\,\,$

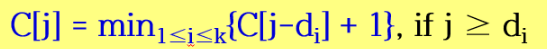
DPCoinChange

• Input: 거스름돈 n원, k개의 동적의 액면 $d_1 > d_2 > ... > d_k = 1$
• Output: C[n]

1. for i = 0 to n C[i] = $\infin$
2. C[0] = 0
3. for j = 1 to n // j는 1원부터 증가하는 (임시) 거스름돈 액수
4. $\,\,\,\,$ for i = 1 to k
5. $\,\,\,\,$ $\,\,\,\,$ if ($d_j \leq$ j) and (C[ j- $d_i$]+1 $<$ C[j])
6. $\,\,\,\,$ $\,\,\,\,$ $\,\,\,\,$ C[j] = C[ j - $d_i$] + 1
7. return C[n]

5.5.2 Procedure

$d_1$ = 16, $d_2$ = 10, $d_3$ = 5, $d_4$ = 1이고, 거스름돈 $n$ = 20일 때

Line 1~2

• 배열 C 초기화 $\infin$

거스름돈 1원 ~ 4원

j는 목표 금액

• 1원
  • C[1] = C[j-1]+1 = C[1-1]+1 = C[0]+1 = 0+1 = 1
• 2원
  • C[2] = C[j-1]+1 = C[2-1]+1 = C[1]+1 = 1+1 = 2
• 3원
  • C[3] = C[j-1]+1 = C[3-1]+1 = C[2]+1 = 2+1 = 3
• 4원
  • C[4] = C[j-1]+1 = C[4-1]+1 = C[3]+1 = 3+1 = 4

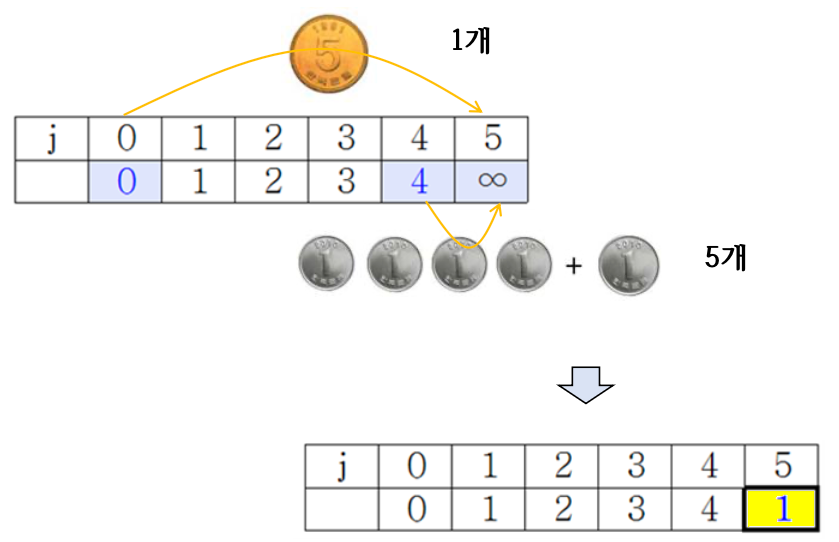
거스름돈 5원

j원을 만들 때 필요한 최소 동전 갯수는 j = 1, 2, 3, 4는 당연히 5원짜리로 만들 수 없으니 기존 값을 사용하고, j = 5에서는 동전 5원을 사용하지 않는 경우인 4 vs. 동전 5원을 사용하는 경우 1 이므로 최솟값 1이 선택된다.

$d_3$ = 5, $d_4$ = 1
5원: C[ j - $d_3$] + 1 = C[5 - 5] +1 = 1
1원: C[ j - $d_4$] + 1 = C[5 - 1] +1 = 5

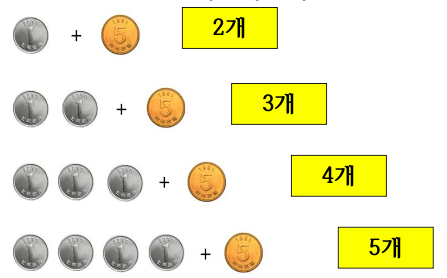
거스름돈 6, 7, 8, 9원

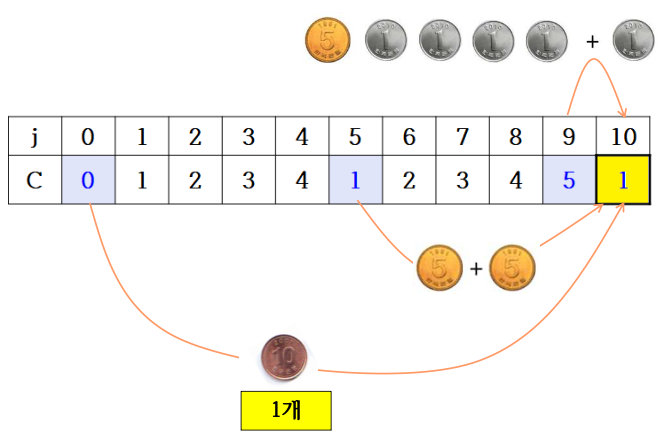
거스름돈 10원

DP 알고리즘은 동전 종류별로 돌아가면서 모두 확인해서 최적값을 갱신한다.
$d_1$은 16원이므로 제외하고, 나머지 3개의 동전 종류별로 확인한다.

j(거스름돈)는 10원

10원: C[ j - $d_2$] + 1 = C[10 - 10] +1 = 1
5원: C[ j - $d_3$] + 1 = C[10 - 5] +1 = 2
1원: C[ j - $d_4$] + 1 = C[10 - 1] +1 = 6

최솟값 1이 기록된다.

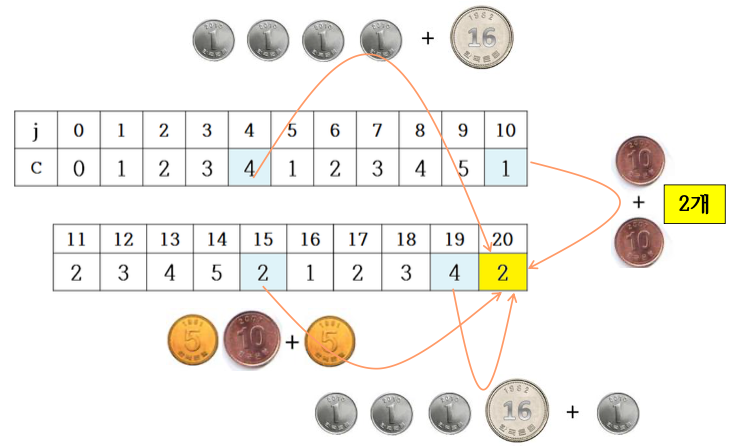
거스름돈 20원

16원: C[ j - $d_1$] + 1 = C[20 - 16] +1 = 5
10원: C[ j - $d_2$] + 1 = C[20 - 10] +1 = 2
5원: C[ j - $d_3$] + 1 = C[20 - 5] +1 = 3
1원: C[ j - $d_4$] + 1 = C[20 - 1] +1 = 5

최솟값인 2가 기록된다.

5.5.3 Result

• 거스름돈 20원에 대한 최종해 = C[20] = 2
• 그리디 알고리즘은 20원에 대해 16원 동전을 먼저 '욕심 내어' 취하고 4원이 남게 되어, 1원 4개를 취하여, 모두 5개의 동전이 해라고 답한다.

5.5.4 Time Complexity

$O(nk)$

• 거스름돈 j가 1원 ~ n원까지 변하며, 각각의 j에 대해서 최대 모든 동전($d_1, d_2, ... , d_k$) k개를 1번씩 고려하기 때문이다.

DP 알고리즘은 최적 부분 구조(최적성 원칙) 특성을 가지고 있다.

• 문제의 최적해 속에 부분 문제의 최적해가 포함되어 있다.
• 그리디 알고리즘(단계별로 보면)도 유사한 속성을 가진다고 볼 수 있다.