6. Sort Algorithm (1)

정렬 알고리즘은 크게 2가지로 나눌 수 있다.

Internal sort

• 입력의 크기가 주기억 장치(RAM)의 공간보다 크지 않은 경우에 수행되는 정렬
• 버블 정렬, 선택 정렬, 삽입 정렬, 합병 정렬, 퀵 정렬, 힙 정렬, 쉘 정렬, 기수 정렬, 이중 피봇 퀵정렬, Time sort

대표적인 알고리즘의 시간 복잡도는 $O(nlogn)$이다.

External sort

• 입력의 크기가 주기억 장치보다 큰 경우에 보조 기억 장치(HDD)에 있는 입력을 여러 번에 나누어 주기억 장치에 읽어 들은 후, 정렬하여 보조 기억 장치에 다시 저장하는 과정 반복
• 다방향 합병(p-way), 다단계 합병(polyphase)

---

6.1 Bubble sort

• 이웃하는 숫자를 비교하여 큰 수를 뒤로 이동시키는 과정을 반복하여 정렬
• 작은 수가 마치 거품처럼 위로 올라가는 것을 연상케한다.

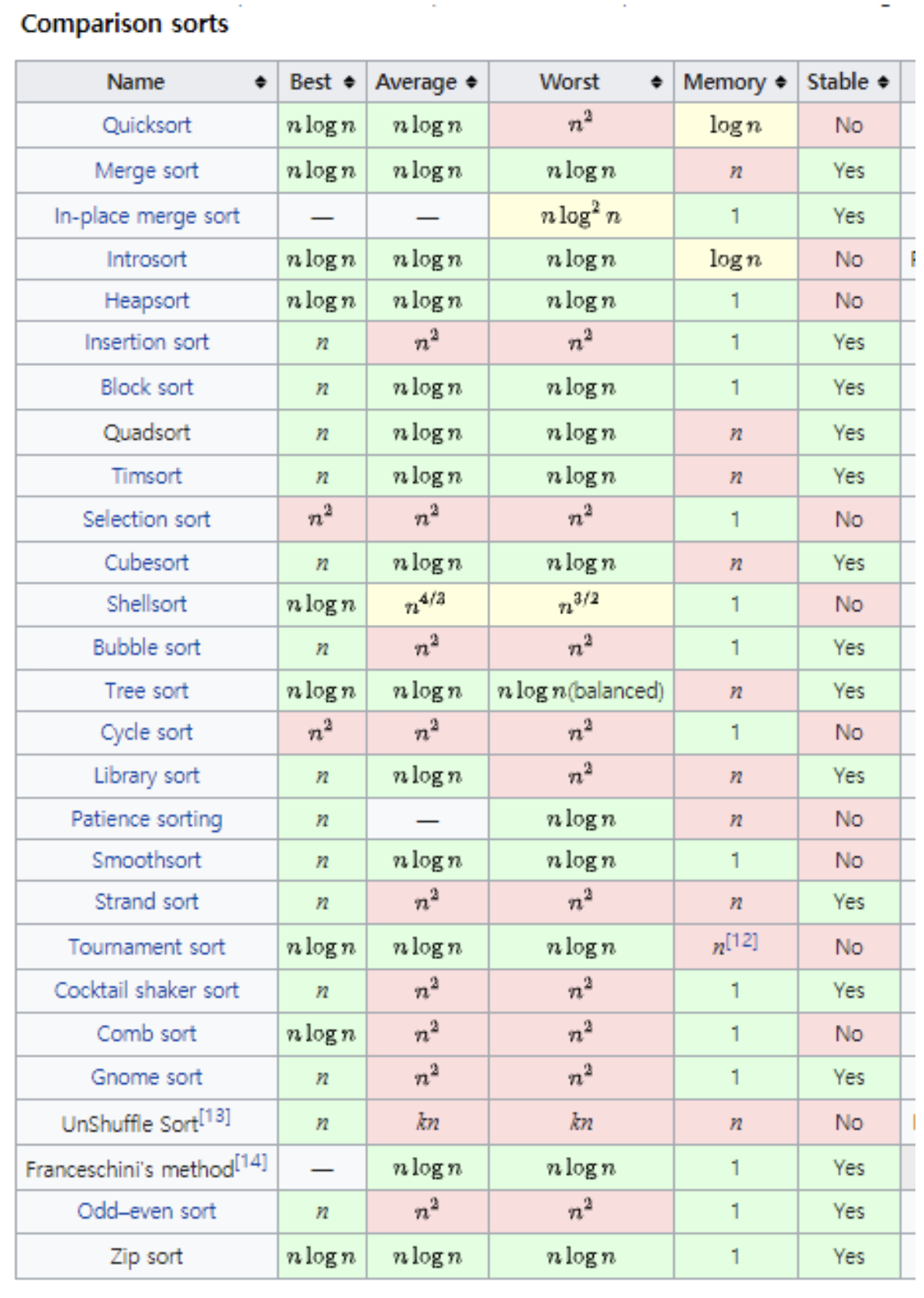
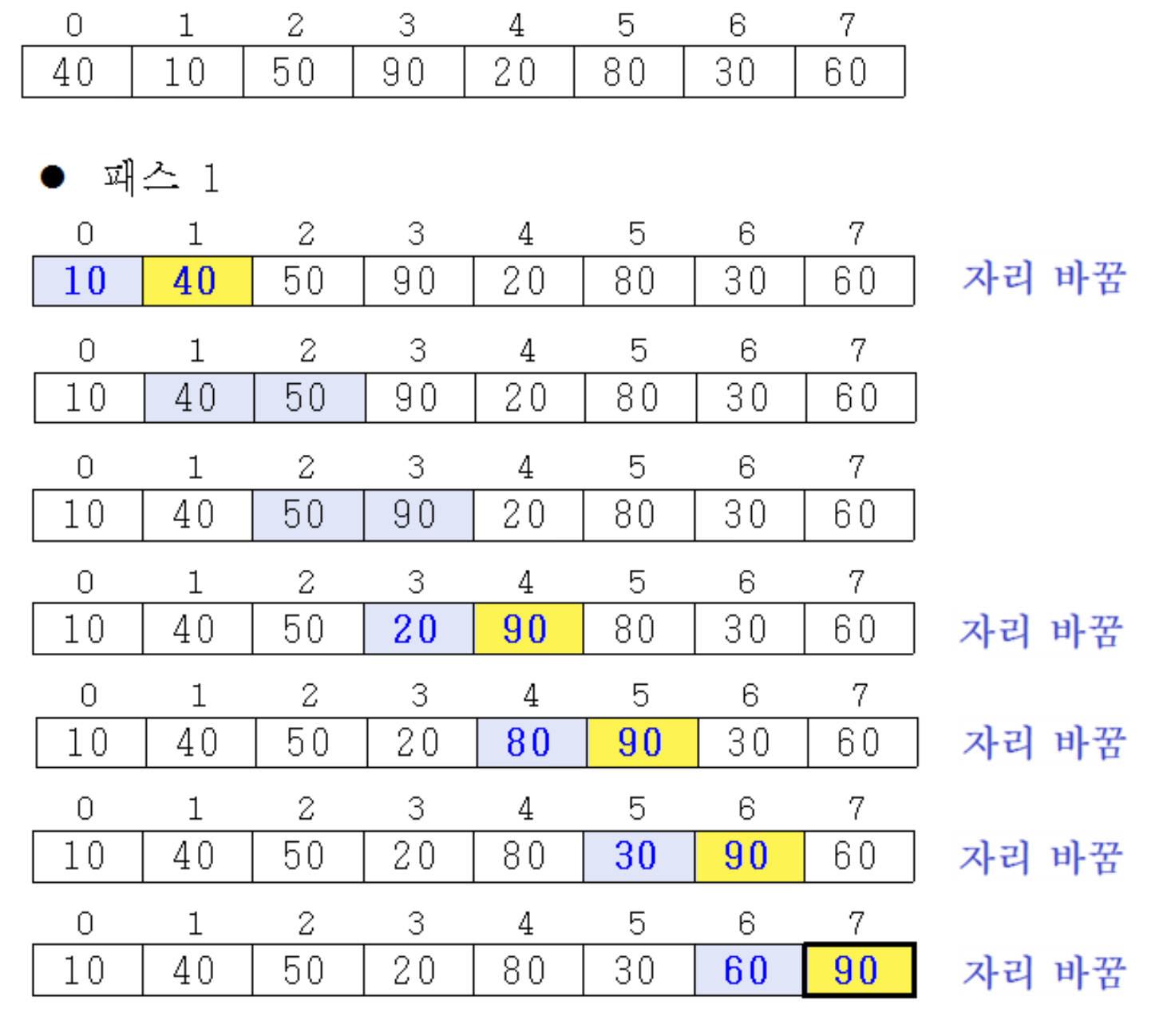
Pass: 입력을 전반적으로 1회 처리하는 것

• 1번째 pass 결과를 살펴보면, 작은 수는 버블처럼 위로 1칸씩 올라감
• 가장 큰 수인 90은 맨 밑(배열의 가장 마지막)에 위치

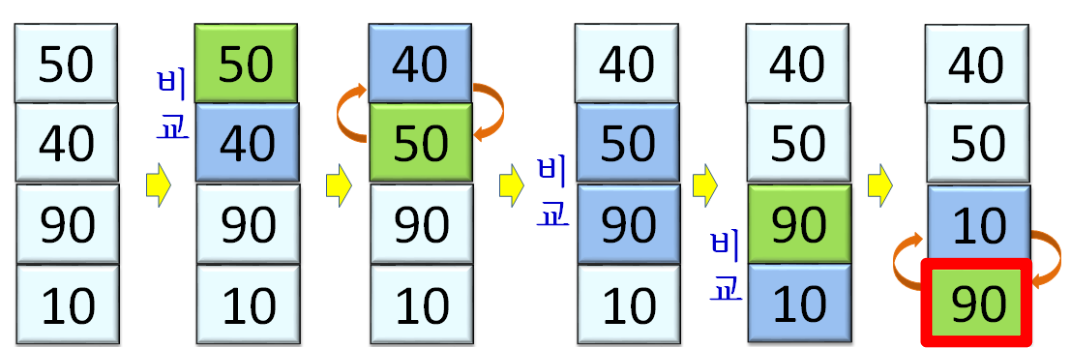
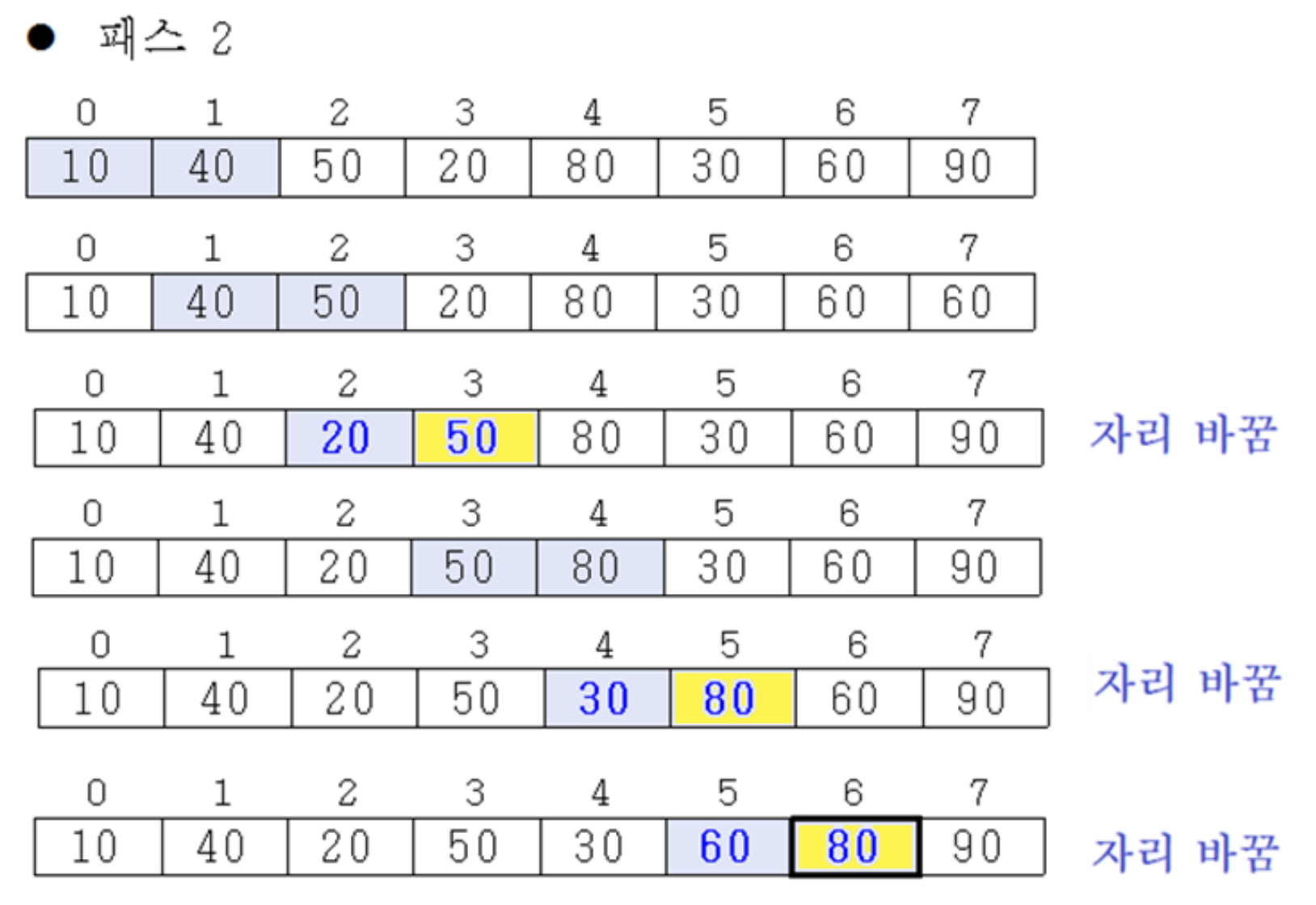
2nd pass

• 이웃하는 원소 간의 비교를 통해 40-50은 그대로 자리에 있고, 50-10이 서로의 자리를 바꿈
• 두 번째로 큰 수인 50이 90의 위에 존재

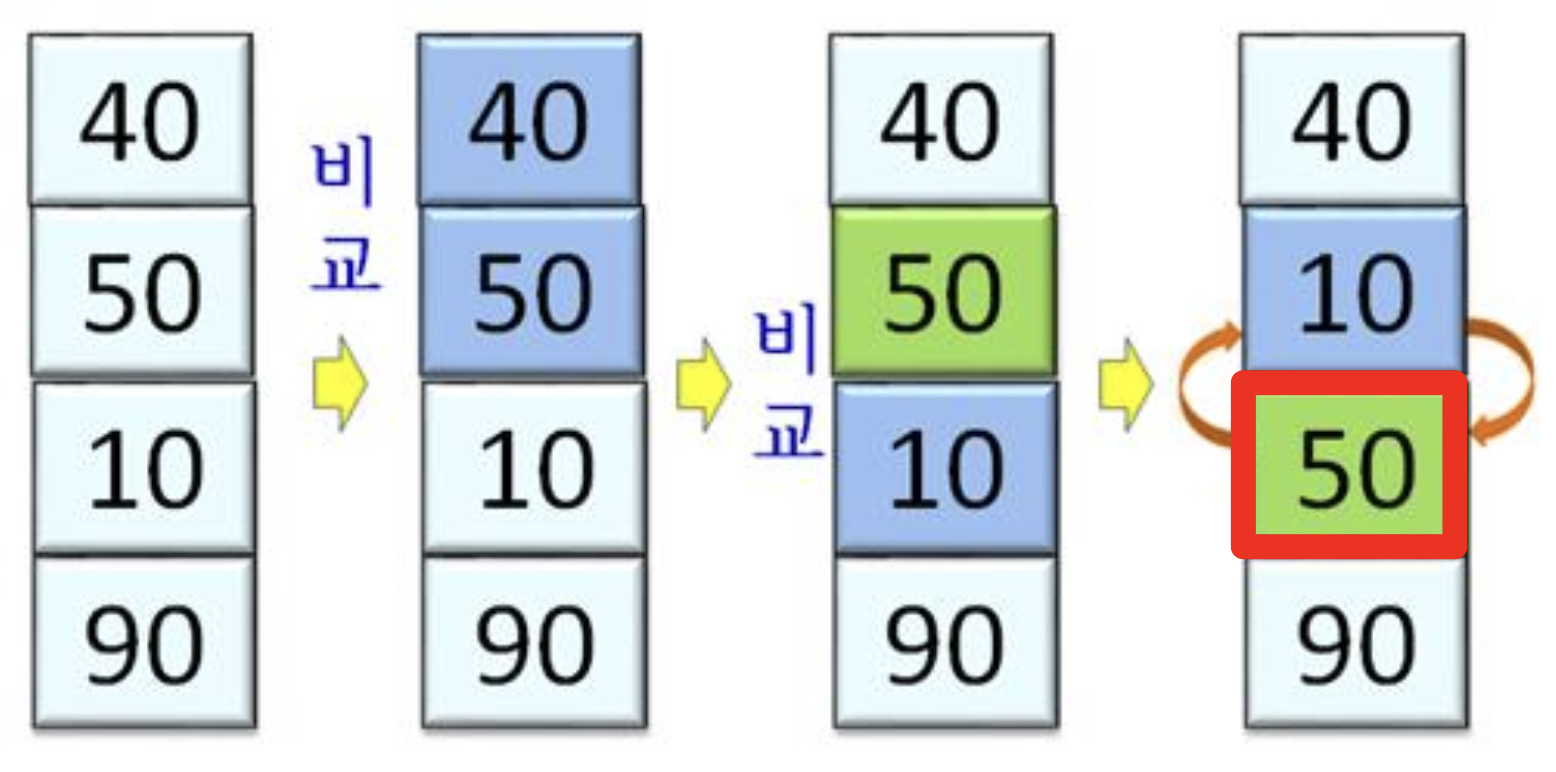
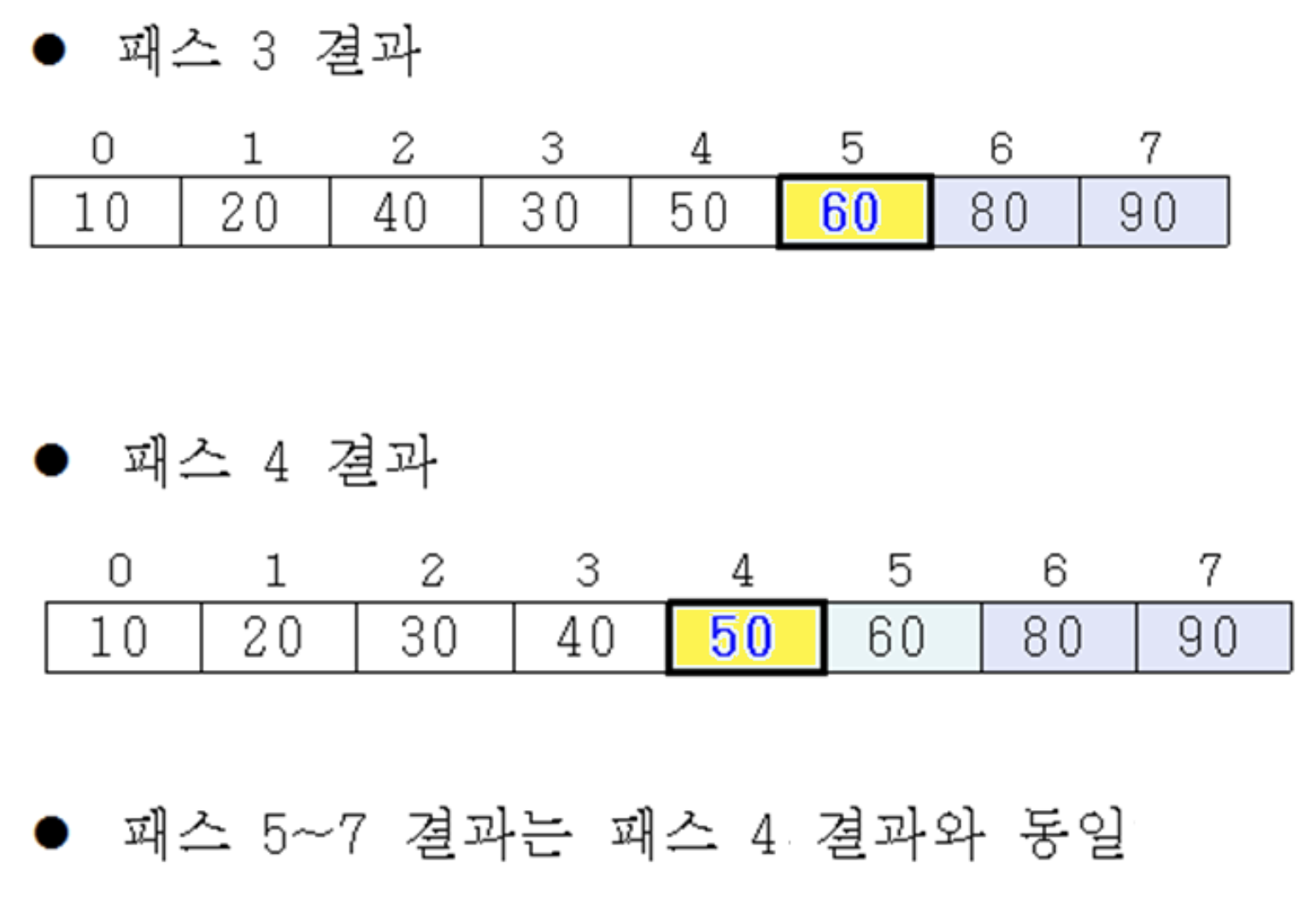
3rd pass

• 이웃하는 원소 간의 비교를 통해 40과 10 교환
• 세 번째로 큰 원소인 40이 두 번째로 큰 원소 50 위에 존재
• n개의 원소가 있으면 n-1번의 pass 수행

6.1.1 BubbleSort()

• Input: 크기가 n인 배열 A
• Output: 정렬된 배열 A

1. for pass = 1 to n-1
2. $\,\,\,\,$ for i = 1 to n-pass
3. $\,\,\,\,$ $\,\,\,\,$ if (A[i-1] > A[i]) // 위의 원소가 아래의 원소보다 크면
4. $\,\,\,\,$ $\,\,\,\,$ $\,\,\,\,$ A[i-1] $\leftrightarrow$ A[i] // 자리 바꿈
5. return A

6.1.2 Procedure

6.1.3 Time complexity

for-loop 속에서 for-loop 수행

• Pass = 1이면, n-1번 비교
• Pass = 2이면, n-2번 비교
  ...
• Pass = n-1이면, 1번 비교
• 총 비교 횟수: (n-1) + (n-2) + ... + 1 = n(n-1)/2
• 안쪽 for-loop의 if 조건이 True일 때, 자리 바꿈은 $O(1)$

$(n-1)/2 \times O(1) = O(n^2) \times O(1) = O(n^2)$

---

6.2 Selection sort

• 입력 배열 전체에서 최솟값을 선택하여 배열의 0번 원소와 자리를 바꾸고, 나머지 원소에서 최솟값을 선택하여 배열의 1번 원소와 자리를 바꾼다.
• 이러한 방식으로 마지막에 2개의 원소 중 작은 것을 선택하여 자리를 바꾼다.

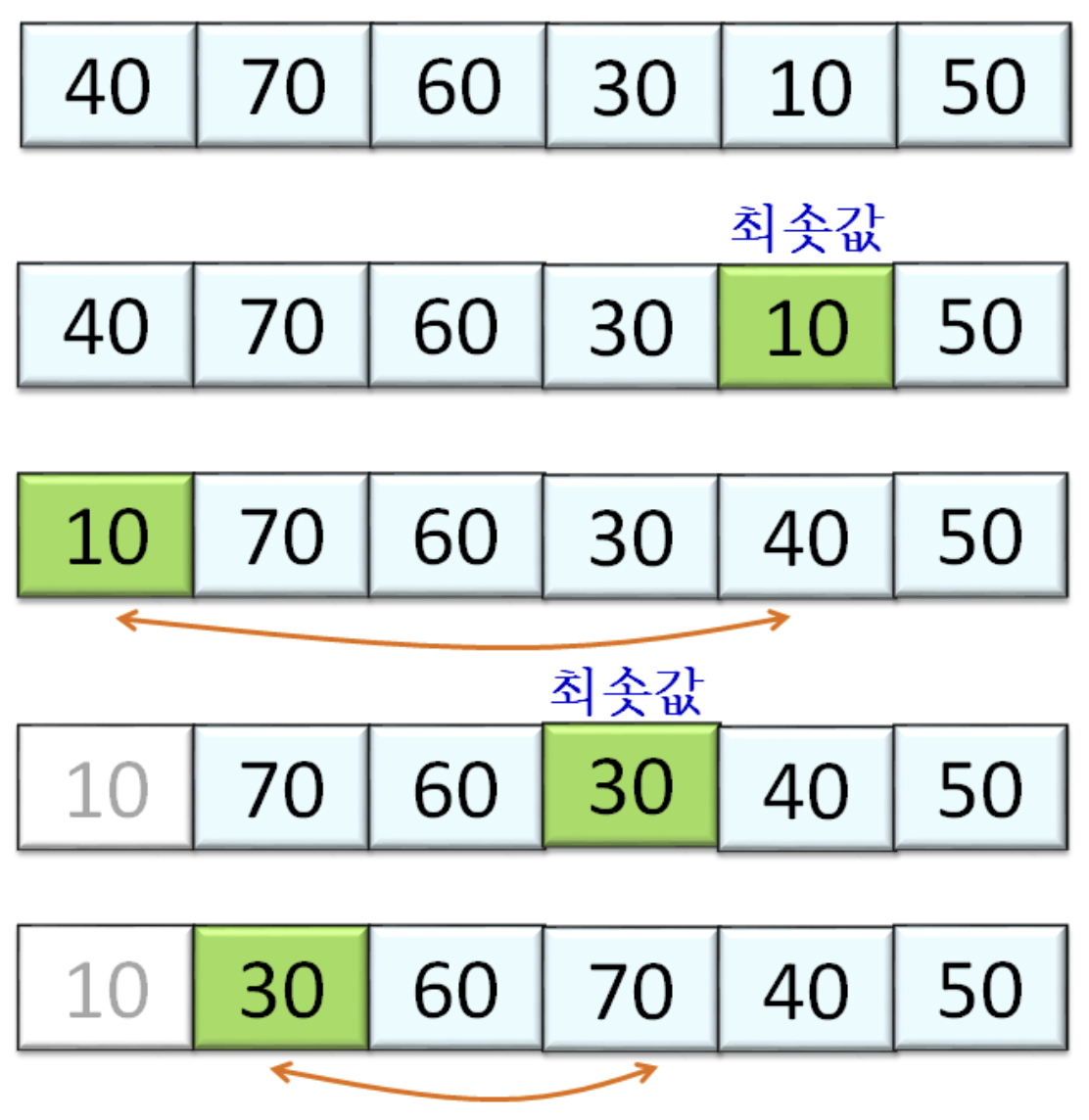
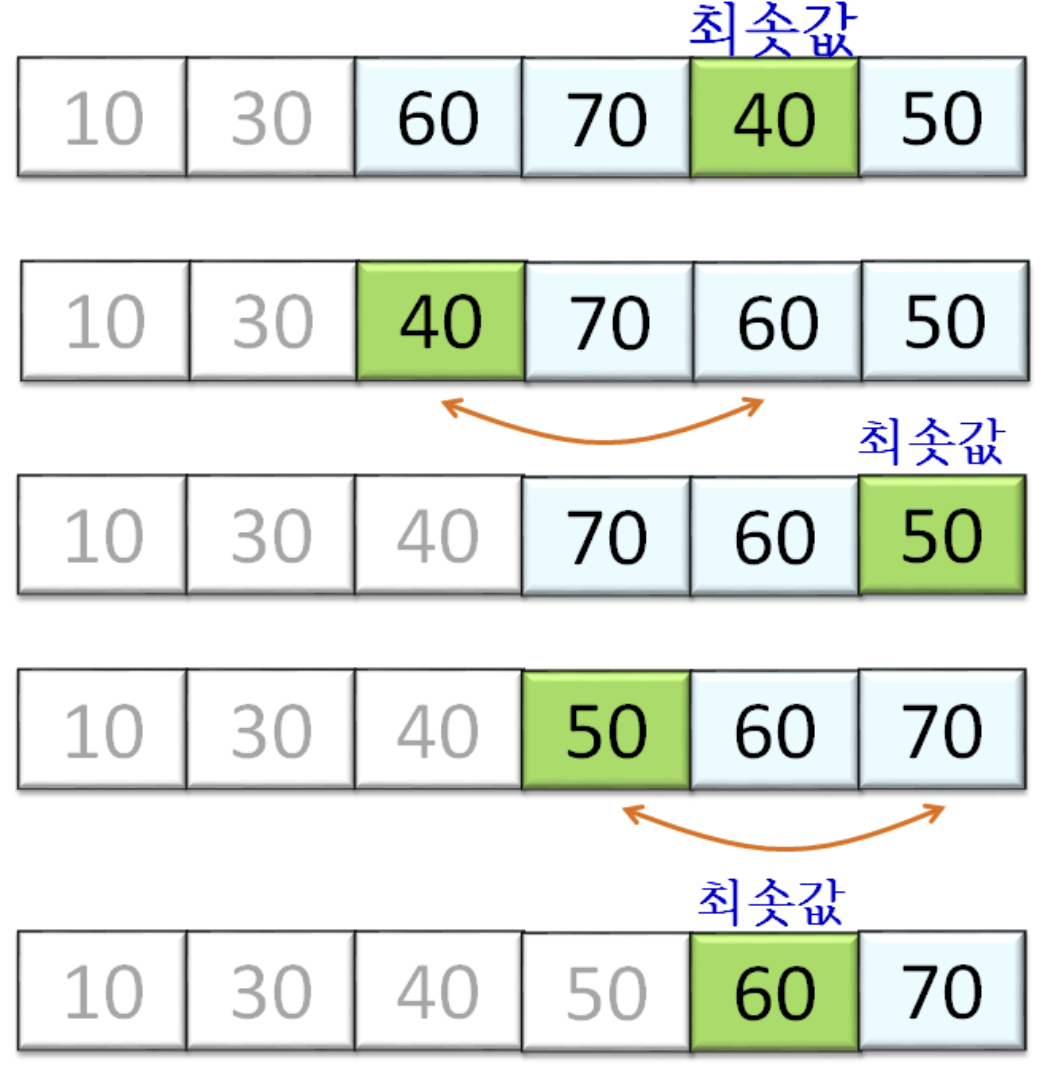
한 번의 pass당 swap이 한 번만 일어나기 때문에, 버블 정렬보다 미세하게 빠르다.

6.2.1 SelectionSort()

• Input: 크기가 n인 배열 A
• Output: 정렬된 배열 A

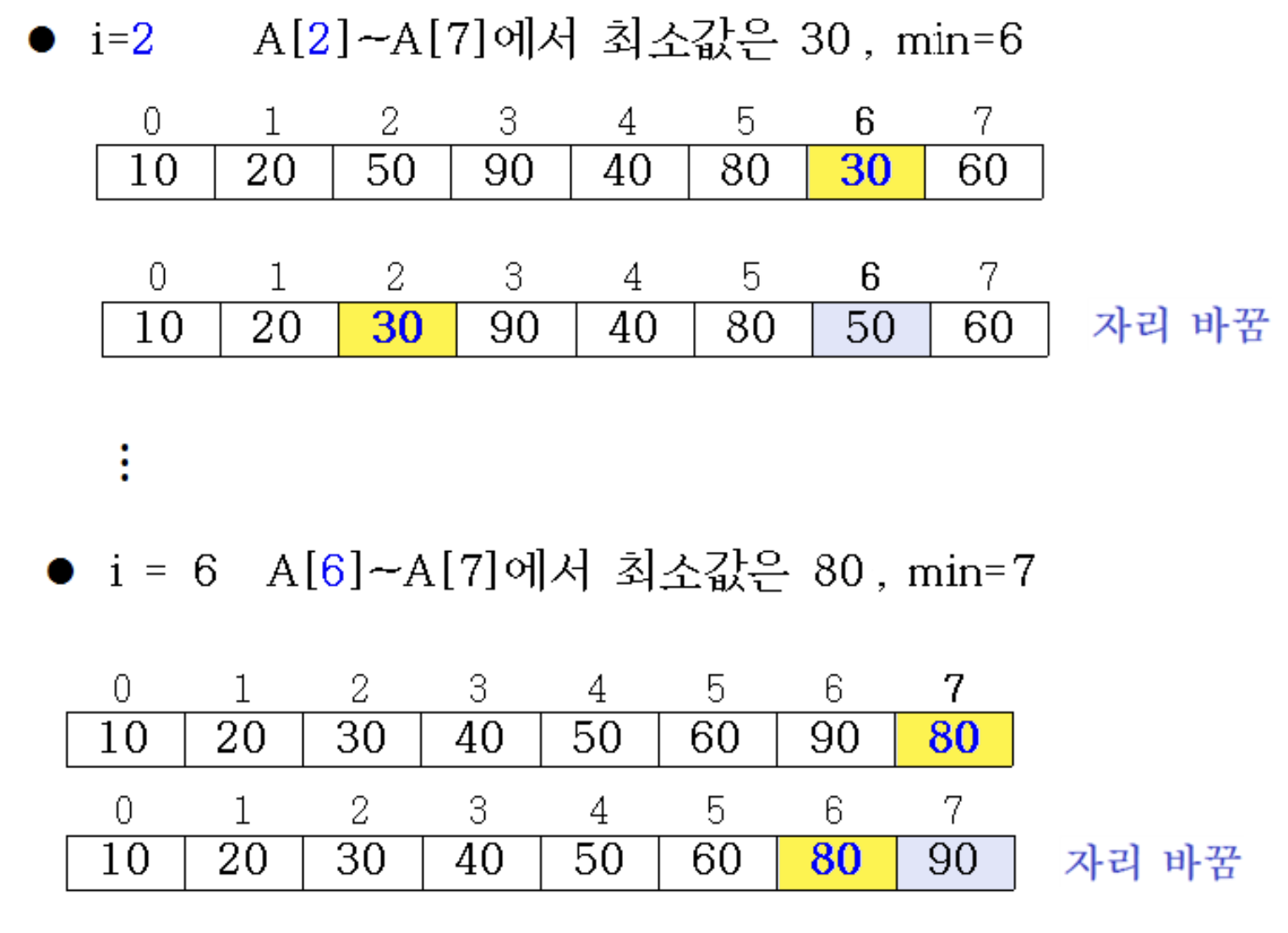
1. for i = 0 to n-2
2. $\,\,\,\,$ min = i
3. $\,\,\,\,$ for j = i+1 to n-1 // A[i]~A[n-1]에서 최솟값 찾기
4. $\,\,\,\,$ $\,\,\,\,$ if A[j] < A[min]
5. $\,\,\,\,$ $\,\,\,\,$ $\,\,\,\,$ min = j
6. $\,\,\,\,$ A[i] $\leftrightarrow$ A[min]
7. return A

6.2.2 Procedure

6.2.3 Time Complexity

• 외부 for-loop는 (n-1)번 수행
  • i = 0; 내부 for-loop는 (n-1)번 수행
  • i = 1; 내부 for-loop는 (n-2)번 수행
    ...
  • 마지막으로 1번 수행
• 내부 for-loop가 수행되는 총 횟수
  • (n-1) + (n-2) + (n-3) + ... + 2 +1 = n(n-1)/2
• loop 내부의 if 조건이 Ture일 때의 자리 바꿈은 $O(1)$

$(n-1)/2 \times O(1) = O(n^2)$

6.2.4 Input insensitive

• 입력이 거의 정렬되어 있든지, 역으로 정렬되어 있든지, 랜덤하게 되어있든지 항상 일정한 시간 복잡도를 나타낸다.
• 입력에 민감하지 않은 알고리즘
• 원소 간의 자리바꿈 횟수가 최소인 정렬

---

6.3 Insertion sort

버블 < 선택 < 삽입

선택 정렬은 정렬되지 않은 부분에서 최솟값을 찾아 한 번에 앞으로 보내고, 삽입 정렬은 정렬되지 않은 부분의 첫 번째 원소를 정렬된 부분의 알맞은 위치에 삽입하는 방식이다.

• 배열을 정렬된 부분(앞부분)과 정렬 안 된 부분(뒷부분)으로 나누고, 정렬 안 된 부분의 가장 왼쪽 원소를 정렬된 부분의 적절한 위치에 삽입하여 정렬되도록 하는 과정을 반복

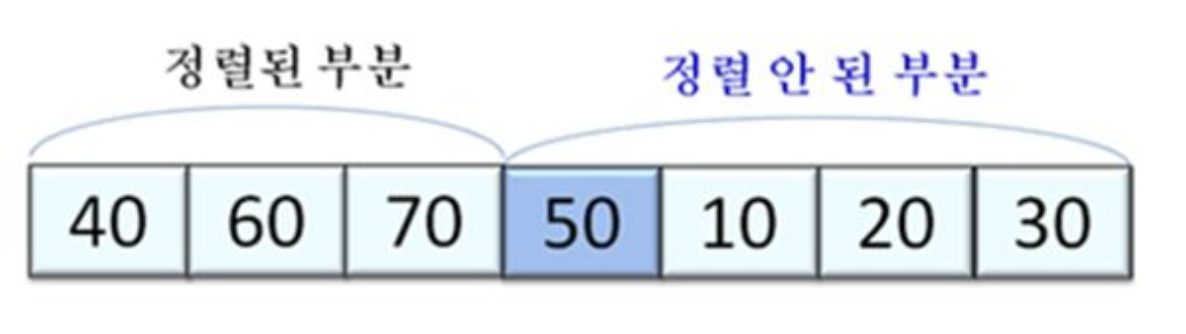
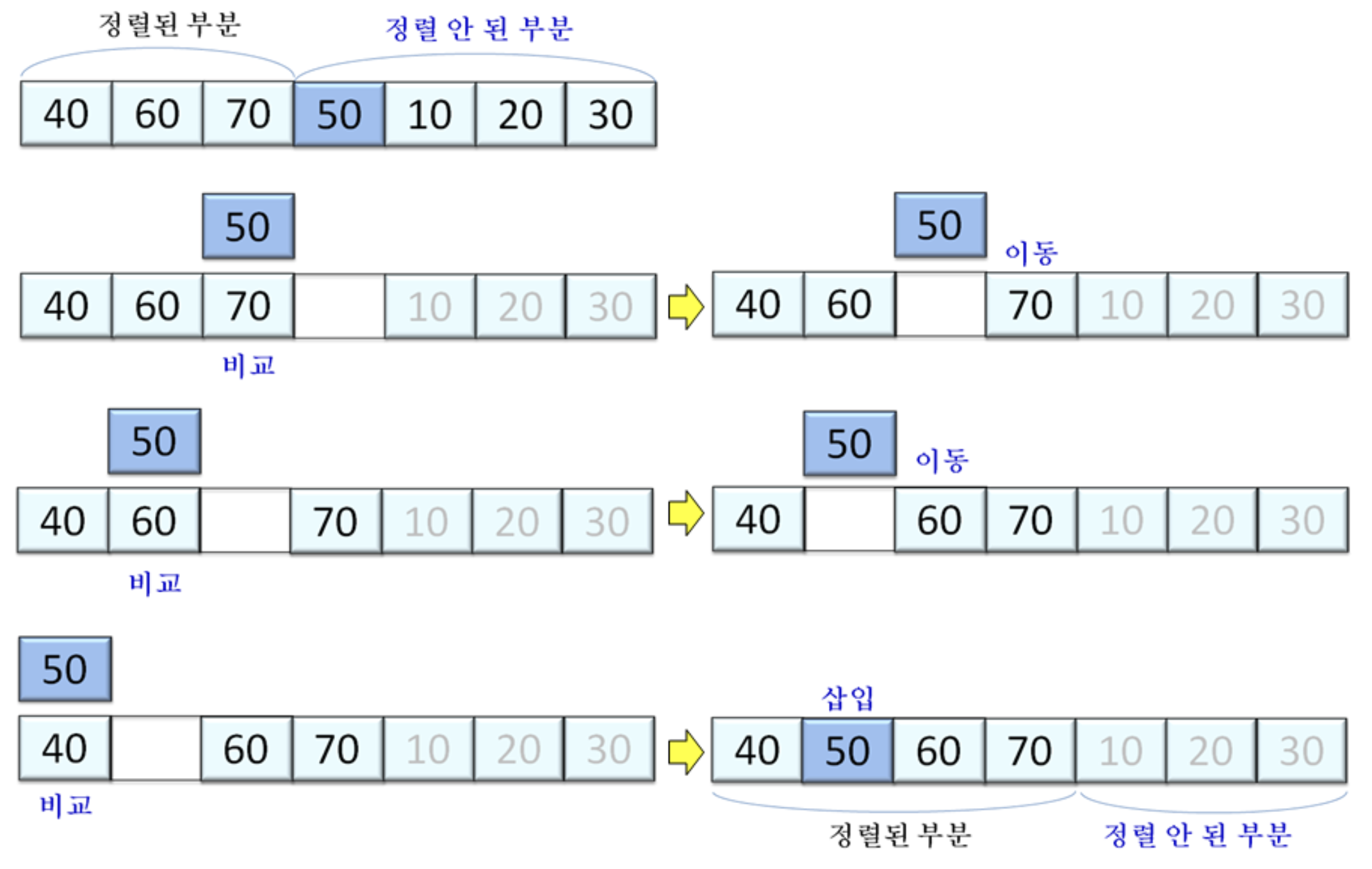
• 정렬 안 된 부분의 숫자 하나가 정렬된 부분에 삽입됨으로써, 정렬된 부분의 원소 수가 1개 늘어나고, 동시에 안 된 부분의 원소 수는 1개 줄어든다.
• 이를 반복 수행하면, 마지막엔 정렬 안 된 부분엔 아무 원소도 남지 않고 입력이 정렬된다.
• 정렬은 배열의 첫 번째 원소만이 정렬된 부분에 있는 상태에서 정렬을 시작한다.

6.3.1 InsertionSort()

• Input: 크기가 n인 배열 A
• Output: 정렬된 배열 A

1. for i = 1 to n-1
2. $\,\,\,\,$ CurrentElement = A[i]
3. $\,\,\,\,$ j $\leftarrow$ i - 1
4. $\,\,\,\,$ while (j >= 0) and (A[j] > CurrentElement){
5. $\,\,\,\,$ $\,\,\,\,$ A[j+1] = A[j]
6. $\,\,\,\,$ $\,\,\,\,$ j $\leftarrow$ j - 1
7. $\,\,\,\,$ }
8. $\,\,\,\,$ A[j+1] $\leftarrow$ CurrentElement
9. return A

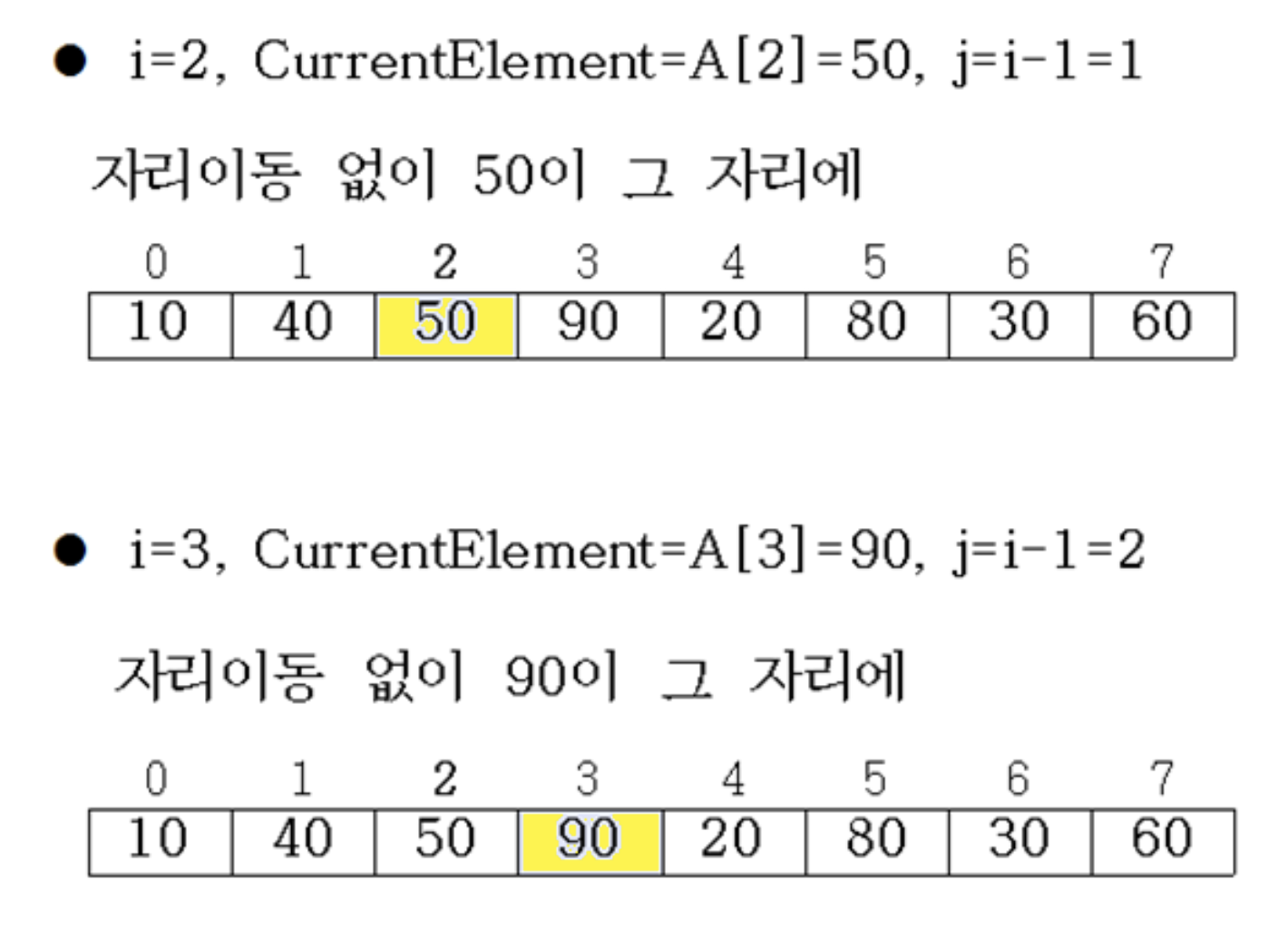
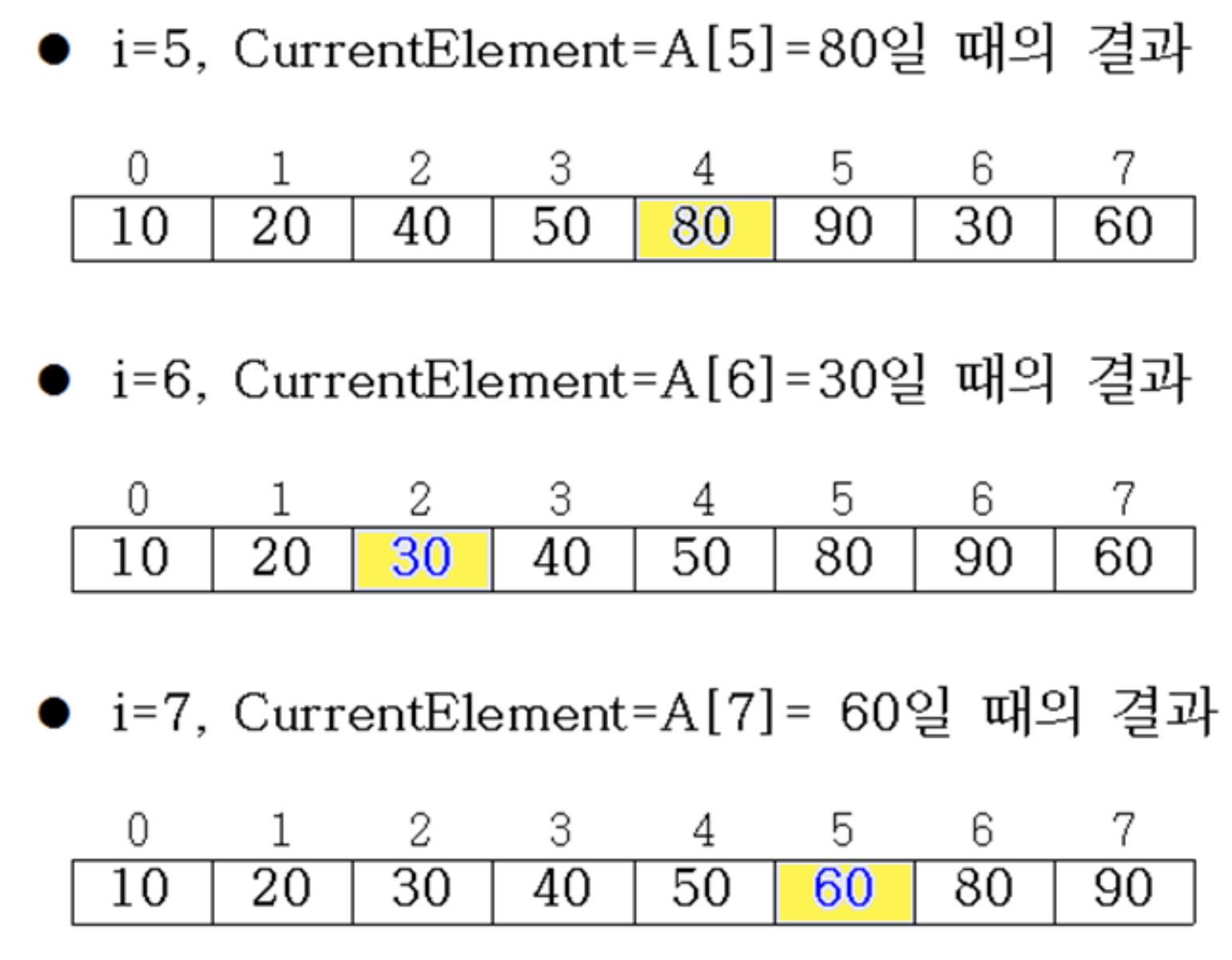
i까지의 앞 부분은 이미 정렬되어 있다고 가정

6.3.2 Procedure

6.3.3 Time complexity

Worst case

• for-loop가 (n-1)회 수행
  • i = 1일 때, while-loop는 1회 수행
  • i = 2일 때, 최대 2회 수행
    ...
  • 마지막으로 최대 (n-1)회 수행
• loop 내부의 line 5 ~ 6이 수행되는 총 횟수
  • 1 + 2 + 3 + ... + (n-2) + (n-1) = n(n-1)/2
• loop 내부는 $O(1)$ 시간

$n(n-1)/2 \times O(1) = O(n^2)$

Best case

• 입력이 이미 정렬되어 있으면, 항상 각각 CurrentElement가 자신의 왼쪽 원소와 비교 후, 자리 이동 없이 원래 자리에 위치하고, while-loop의 조건이 항상 False이므로 원소의 이동도 전혀 없다.
  • 따라서 (n-1)번의 비교만에 정렬을 마친다.
  • 이때가 삽입 정렬의 최선, $O(n)$

실제로 알고리즘을 사용할 때는, 이미 어느 정도 정렬된 것을 다루는 경우가 많기 때문에 삽입정렬이 유용하다.

Average case

• CurrentElement가 자신의 자리 포함 앞부분의 각 원소에 자리잡을 확률이 같다고 가정하여 분석하면
• $O(n^2/4) = O(n^2)$

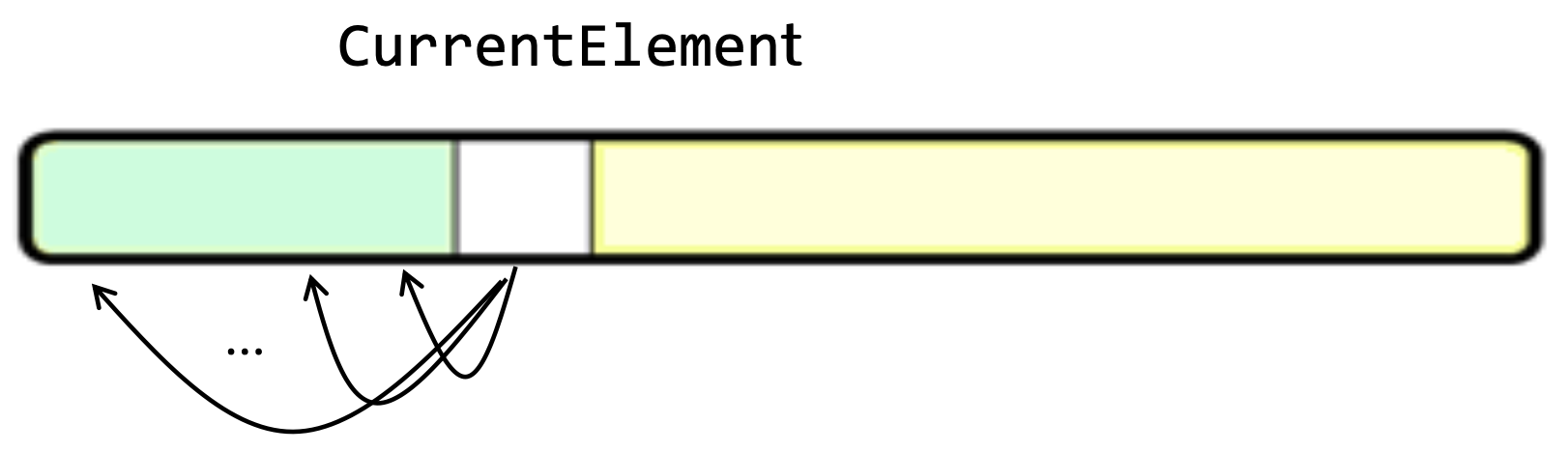
• 현재 원소가 각각 앞부분 각각 원소에 자리 잡을 확률이 같다(균등 분포)고 가정한다.
• 정렬된 부분의 길이가 m이고, 전체 배열의 원소 개수는 n이다. 모든 원소가 정렬된 구간의 어디에나 들어갈 수 있으니까, 평균적으로는 정렬된 부분의 중간 m/2을 비교해야 맞는 차리를 찾는다.
• $\sum_{m=1}^{n-1} \frac{m}{2} = \frac{1}{2} \cdot \frac{(n-1)n}{2} = \frac{n^2}{4} - \frac{n}{4}$

6.3.4 Characteristic

• 거의 정렬된 입력에 대해서 다른 정렬 알고리즘보다 빠르다.
  • e.g. 입력이 앞부분은 정렬되어 있고, 뒷부분(전체의 20% 이하)에 새 데이터가 있는 경우
• 입력의 크기가 작을 때 매우 좋은 성능을 보임
• 퀵 정렬, 합병 정렬에서 입력 크기가 작아지면 순환 호출을 중단하고 삽입 정렬 사용
• Time sort에서는 입력 크기가 64이하면 삽입 정렬 호출

---

6.4 Shell sort

• 버블 정렬이나 삽입 정렬이 수행되는 과정
  • 기껏해야 이웃하는 원소의 자리 바꿈
• 버블 정렬의 수행 과정
  • 작은 숫자가 배열의 앞부분으로 매우 느리게 이동
• 삽입 정렬에서 마지막 원소가 가장 작은 숫자라면
  • 그 숫자가 배열의 맨 앞으로 이동해야 하므로, 모든 다른 숫자들이 1칸씩 오른쪽으로 이동

삽입 정렬을 이용해 배열 뒷부분의 작은 숫자를 앞부분으로 빠르게 이동시키고, 동시에 앞부분의 큰 숫자는 뒷부분으로 빠르게 이동시키자.

6.4.1 Gap

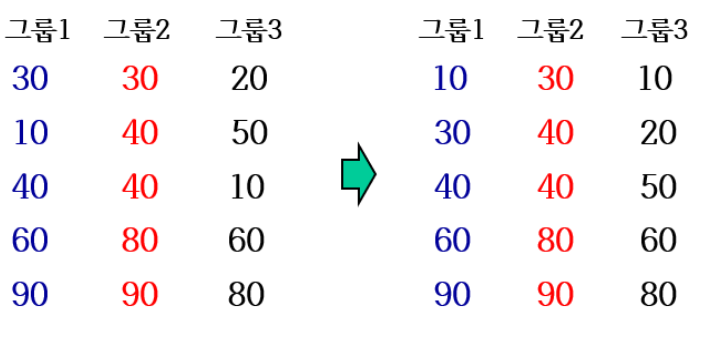
간격이 5인 숫자 그룹

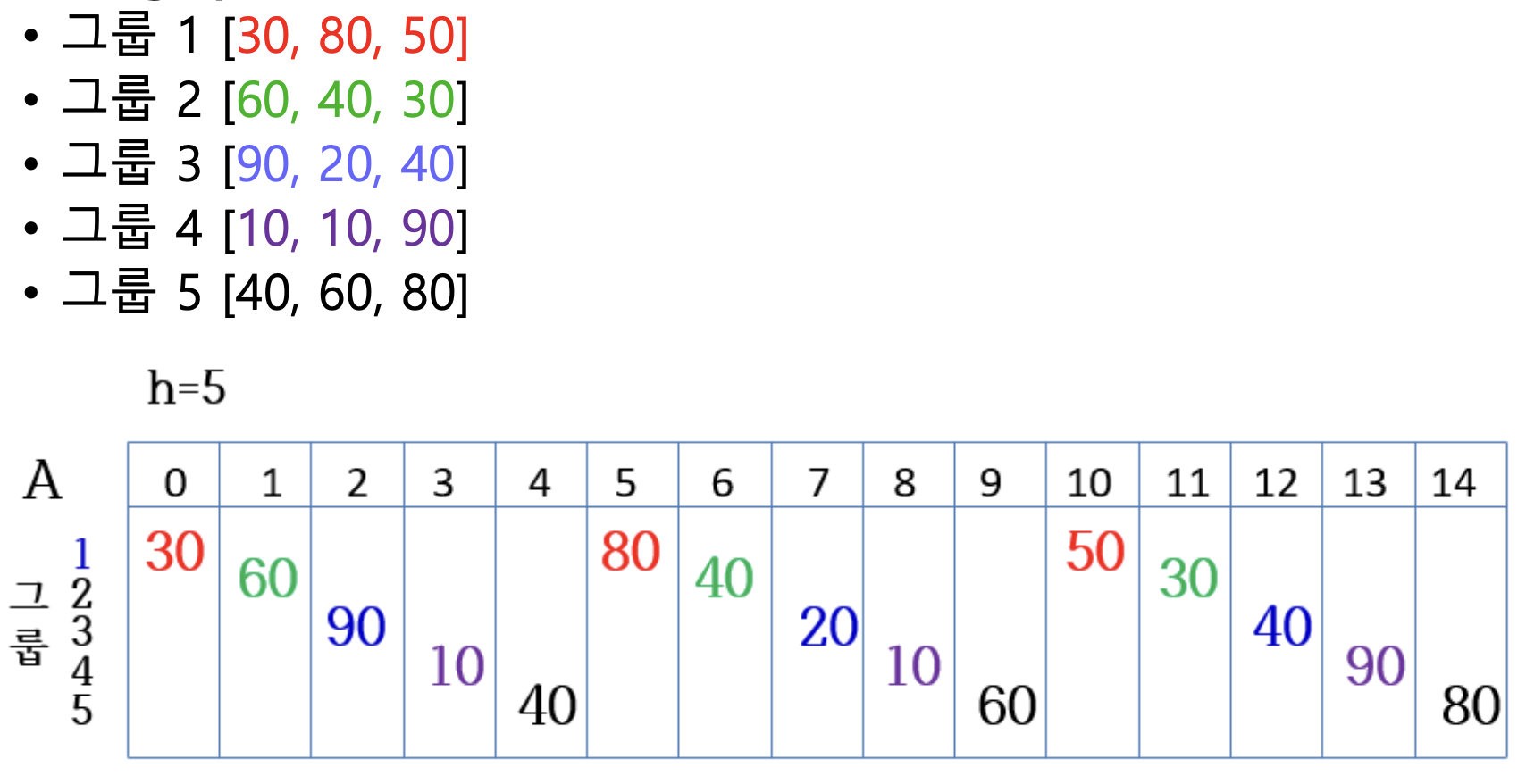
각 그룹별로 삽입 정렬 수행한 결과

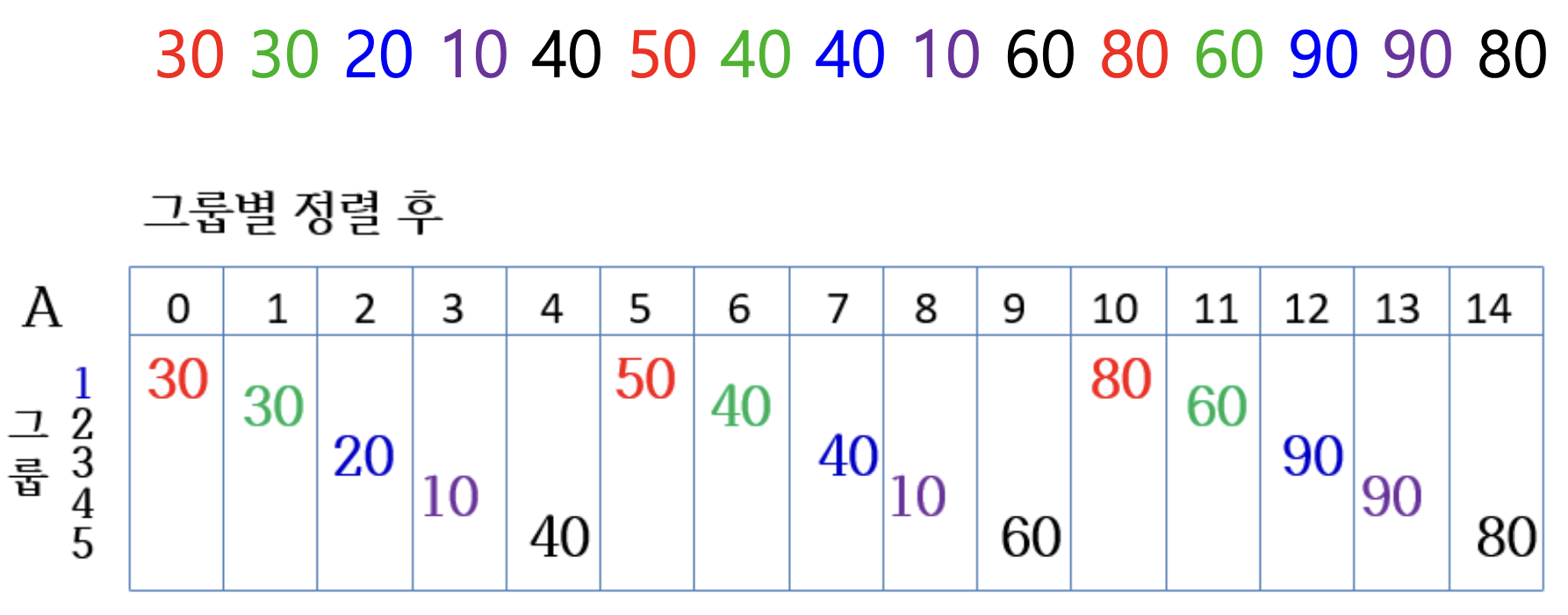
간격이 5인 그룹별로 정렬한 결과

• 80과 90 같은 큰 숫자가 뒷부분으로
• 20과 30 같은 작은 숫자가 앞부분으로

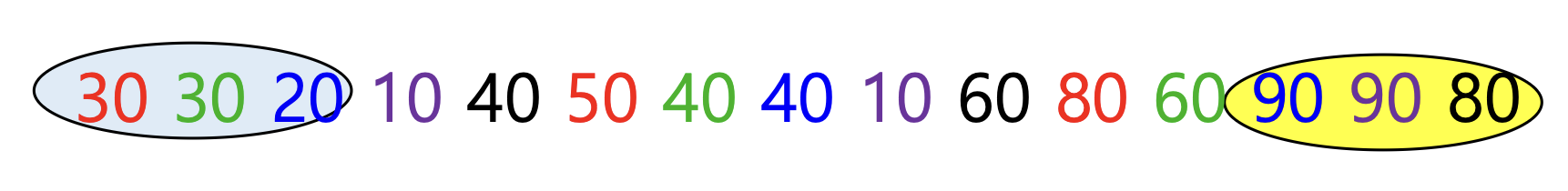
간격 조절

• 다음엔 간격을 5보다 작게 하여(e.g. 3) 3개의 그룹으로 나누어 각 그룹별로 삽입 정렬 수행
• 마지막에는 반드시 간격을 1로 놓고 수행
  • 다른 그룹에 속해 서로 비교되지 않은 숫자가 있을 수 있기 때문
  • 모든 원소를 1개의 그룹으로 여기는 것으로 삽입 정렬

6.4.2 ShellSort()

• Input: 크기가 n인 배열 A
• Output: 정렬된 배열 A

1. for each gap h = [h_0 > h_1 > ... >h_k = 1]
2. $\,\,\,\,$ for i = h to n-1
3. $\,\,\,\,$ $\,\,\,\,$ CurrentElement = A[i]
4. $\,\,\,\,$ $\,\,\,\,$ j = i
5. $\,\,\,\,$ $\,\,\,\,$ while ( j >= h) and (A[j-h] > CurrentElement)
6. $\,\,\,\,$ $\,\,\,\,$ $\,\,\,\,$ A[j] = A[j-h]
7. $\,\,\,\,$ $\,\,\,\,$ $\,\,\,\,$ j = j-h
8. $\,\,\,\,$ $\,\,\,\,$ A[j] = CurrentElement
9. return A

h 자체는 하나의 gap 값이지만, 바깥 반복문에서 gap list를 하나씩 꺼내 쓰는 형태로 생각하면 된다.

6.4.3 Comparison order

• Line 2 ~ 8: for-loop에서 간격 h에 대해 그룹별로 삽입 정렬이 수행되는데, 실제 자리바꿈을 위한 원소 간의 비교는 아래와 같은 순서로 진행

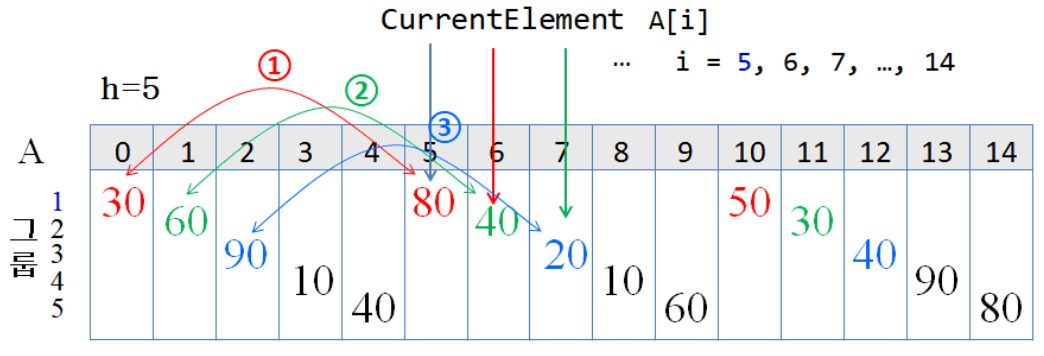
앞에 gap만큼 떨어진 원소랑만 한번 비교하고 끝나는 게 아니라, 현재 값이 삽입될 올바른 위치가 나올 때까지 계속 gap만큼 건너뛰며 비교한다.

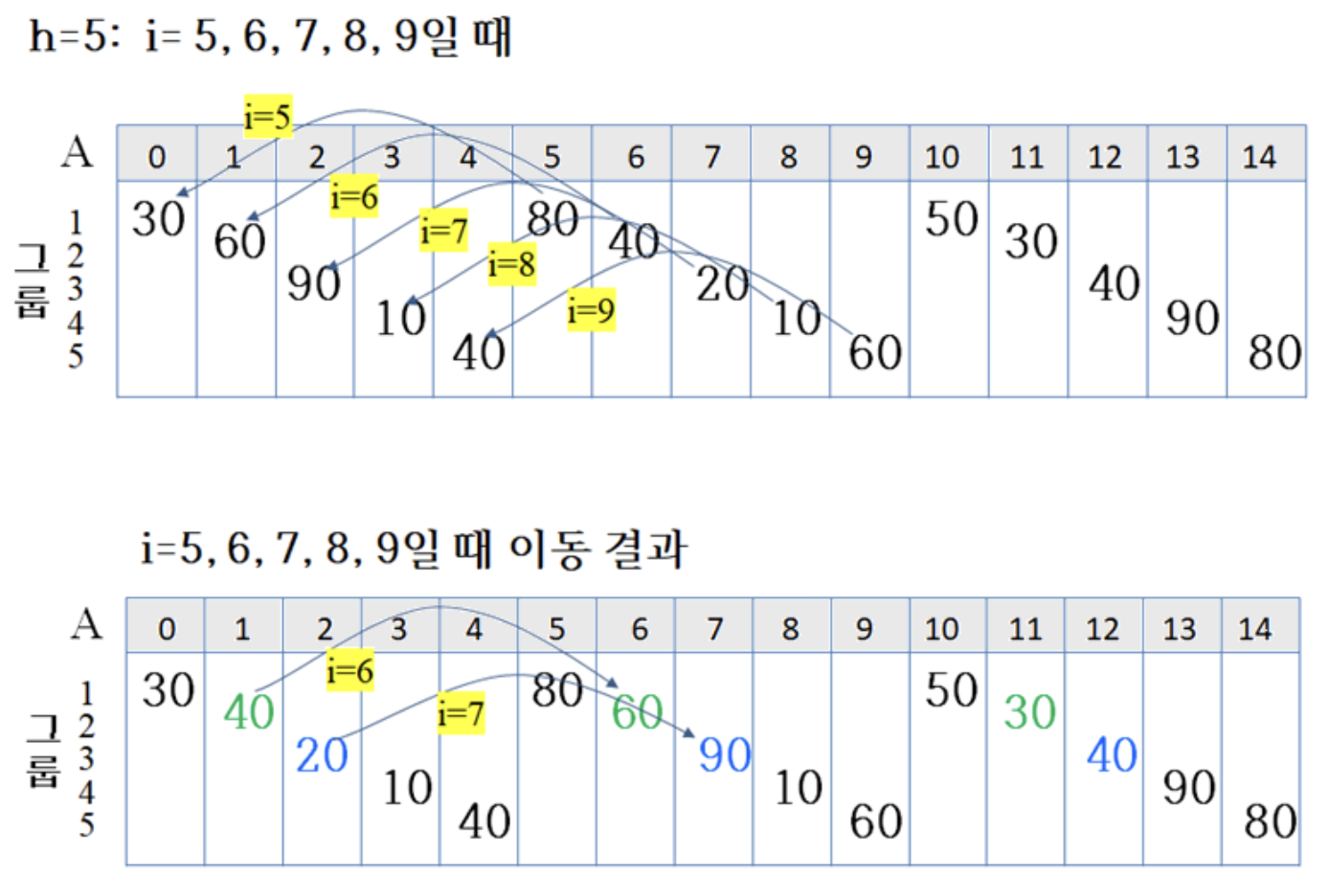
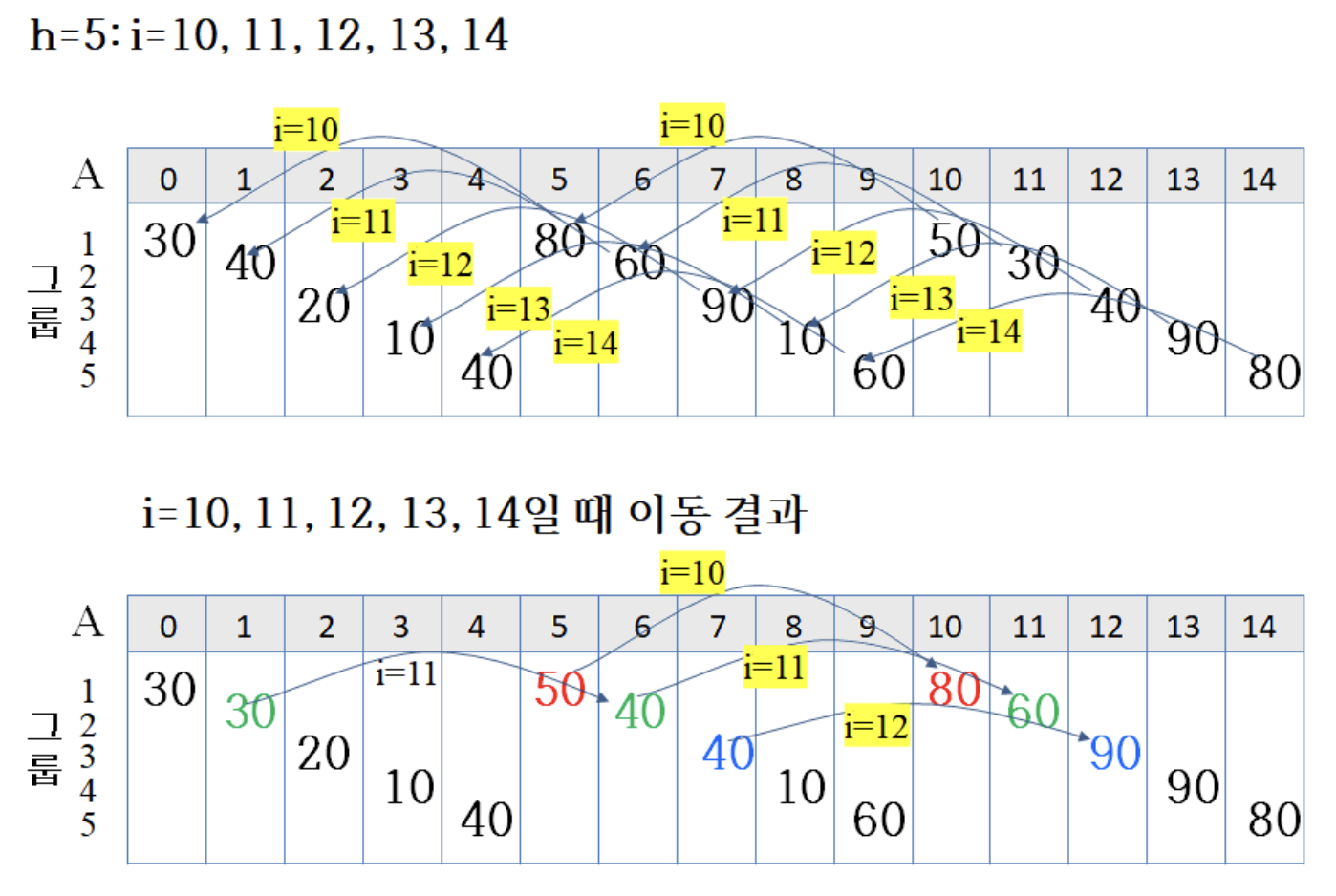
6.4.4 Procedure

h = 5일 때,

• 30 30 20 10 40 50 40 40 10 60 80 60 90 90 80

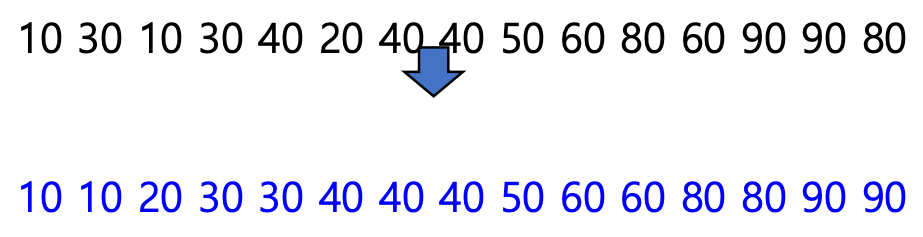
h = 3일 때,

• 배열의 원소가 3개의 그룹으로

h = 1일 때,

• 삽입 정렬과 동일

6.4.5 Time complexity

• 사용하는 간격에 따라 분석 필요
• Worst case: Hibbard의 간격 $2^k-1$
  • $2^k-1(2^k-1, ..., 15, 7, 5, 3, 1)$을 사용하면 $O(n^{1.5})$
• 지금까지 알려진 가장 좋은 성능을 보인 간격
  • $1, 4, 10, 23, 57, 132, 301, 701, 1750$ Marcin Ciura
• 쉘 정렬의 시간 복잡도는 아직 풀리지 않은 문제
  • 가장 좋은 간격을 알아내야 하는 것이 선행되어야 하기 때문

6.4.6 Characteristic

• 입력 크기가 매우 크지 않은 경우에 매우 좋은 성능
• 임베디드 시스템에서 주로 사용
  • 간격에 따른 그룹별 정렬 방식이 H/W로 정렬 알고리즘을 구현하는 데에 적합