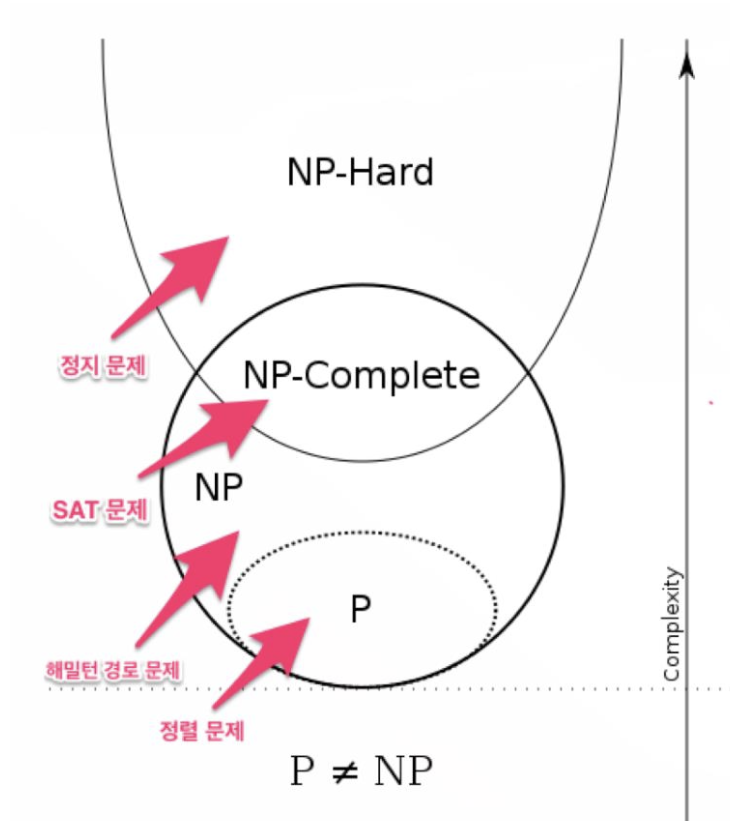
7.1 Classification of problems
7.1.1 Deterministic vs. Non-Deterministic
Deterministic
- One possible option at each decision step
- E.g., Dijkstra algorithm to find the shortest path
- Generate one corret solution
Non-Deterministic
- Many possible options at each decision step
- A set of possible states or solutions are generated
- Generate many candidate solutions
- Check wheter thry are corret or not
- We can use search algorithm
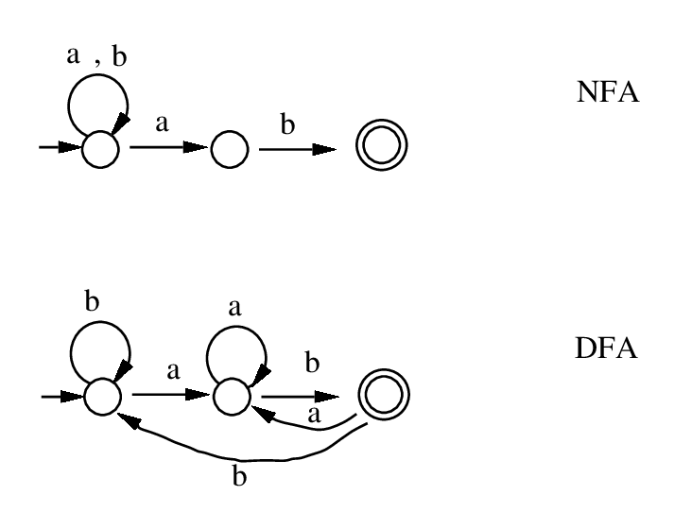
- NFA는 입력 'a'가 들어왔을 때 현재 상태에서 다음 상태가 여러 개(a,b(1), a(2))라서 어떤 경로로 갈지 미리 단정할 수 없다.
- 반면 DFA는 입력마다 모든 상태에서 항상 하나의 명확한 경로만 존재한다.
Deterministic은 입력에 대해 항상 하나의 상태로 정확히 이동하는 것을 의미하고, Non-Deterministic은 매 입력마다 여러 상태로 갈 수 있는 가능성을 모두 남겨두기 때문에 모든 후보 경로를 추적하며 정답이 있는지 검사해야 한다.
7.1.2 P vs. NP Problems
P Problem
- There exists a deterministic algorithm running in polynomial time
항상 결정론적인 알고리즘으로 다항식 시간 안에 정답을 도출할 수 있는 문제를 의미한다.
NP Problem
- There exsists a non-deterministic algorithm (generate candidate solutions)
- Verifying process runs in polynomial time
NP 문제는 Non-polynomial이 아니라 Non-deterministic의 약자, 비결정론적인 알고리즘으로 다항식 시간 내에 검증이 가능한 문제를 뜻한다. 1개 이상의 정답 후보가 생성되고, 후보가 실제로 정답인지 아닌지 검증하는 과정이 다항식 시간 내에 수행되어야 한다.
정답이 yes인 경우에 답을 하나 줬다고 했을 때, 그게 진짜 맞는지 여부를 다항식 시간 안에 확인할 수 있는 결정 문제들의 집합
Polynomial vs non-polynomial time algorithm
- Polynomial time
- Worst-case running time is , for some constant k
- E.g., , , ,
- Non-polynomial time
- E.g., , ,
- P is in NP
- Generate only one solution in polynomial time
- Verifying runs in polynomial time
- NP is in P? (Not proven)
- Means nobody found P algorithm
- (to prove existence, we need to show that all algorithms are not in P)
P is in NP는 이미 증명되어 있기 때문에 NP is in P가 증명되면 P = NP가 될 것이다.
7.1.3 Verification
Decision problems
- Given an input and a question regarding a problem, determine if the answer is "yes" or "no"
Optimization problems
- Find a solution with the "best" or "optimum" value
- Optimization problems can be cast as decision problems that are easier to study
- E.g., Shortest path:G = unweighted directed graph
- Find a path between u and v that uses the fewest edges (optimization)
- Does a path exist from u to v consisting of a most k edges? (decision)
- E.g., Shortest path:G = unweighted directed graph
가장 좋은 값을 찾아내는 최단 경로 찾기 등의 문제가 최적화 문제이고, 어떤 조건이 특정 값을 넘지 않는지 y/n로 답하는 문제가 결정 문제이다.
E.g., Hamiltonian Cycle
- Optimization problems
- Given a graph G = (V, E), determine cycle that contains each and every vertex in V only once

- Decision problems
- Given a directed graph G = (V, E), is there a cycle that contains each and each vertex in V only one? y/n
같은 문제에 대해서 결정 문제는 이러한 사이클이 그래프에 있는지 여부만 판단한다.
7.1.4 Intractable Problems
- Problems in P are called tractable
- Problems not in P are intractable or unsolvable
- Can be solved inreasonable time only for small input size
- Or, can not be solved at all
NP 문제라는 건 문제의 어려움을 의미한다.
- Are non-polynomial algorithms always wort than polynomial ones?
- is technically tracable, but almost impossible to solve
- is technically intractable, but possible to solve for reasonable size n
Intractable does not mean
- Brute-force algorithms are the only option
- All instances of the problem are equally hard
- It is hard to get approximate answers
Brute-force만 가능하다거나, 모든 인스턴스가 다 꼭같이 어렵다는 뜻이 아니다. 어느 경우에는 근삿값을 빠르게 구할 수 있는 알고리즘이 존재하기도 한다.
How to know complexity of your problems?
- Design algorithm until we find one running in polynomial time
- Impossible
- See whether your problem is in NP-complete
- You do not need to spend more time to find polynomial algorithms
무식하게 다항시간 알고리즘을 찾으려고 계속 설계하는 건 실상 불가능하다. 대신 그 문제가 NP-complete인지 확인하자. 먼저 문제가 NP에 속함을 보이고 NP-complete로 알려진 문제에서 현재 문제가 다항시간 환원을 할 수 있으면 NP-complete가 된다.
7.1.5 NP Problem Set
- P 문제 집합과 NP-Complete 문제 집합을 둘 다 포함하는 집합
- NP 문제 집합에 속한 문제를 NP 문제라고 한다.
- NP 문제는 Non-deterministic Polynomial time 알고리즘을 가진 문제이다.
NP Algorithm
- Non-deterministic Polynomial time Algorithm
- 첫 번째 단계
- 주어진 입력에 대해서 하나의 해를 추측하고
- 두 번째 단계
- 그 해를 다항식 시간에 확인한 후에
- 그 해가 '맞다/아니다'라고 답한다.
해를 찾는 알고리즘이 아니라, 해를 다항식 시간에 확인하는 알고리즘이다.
7.1.6 The relationship
- P 문제, NP-Complete 문제, NP 문제 집합 사이의 관계
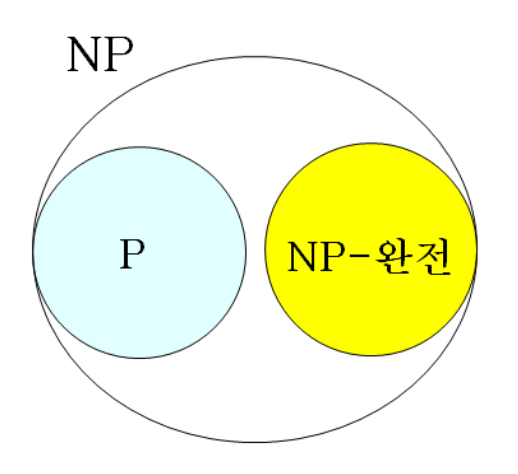
P NP ?
- P 문제는 다항식 시간에 해결할 수 있는 문제
- NP 문제의 해를 '다항식 시간에 검증할 수 있다'는 성질과 대응
- P 문제는 NP 알고리즘처럼 해를 추측하는 단계가 필요 없으며, 다항식 시간 안에 직접 해를 구해 검증 결과를 참으로 판단한다.
7.2 NP-Completeness
7.2.1 NP-Completeness
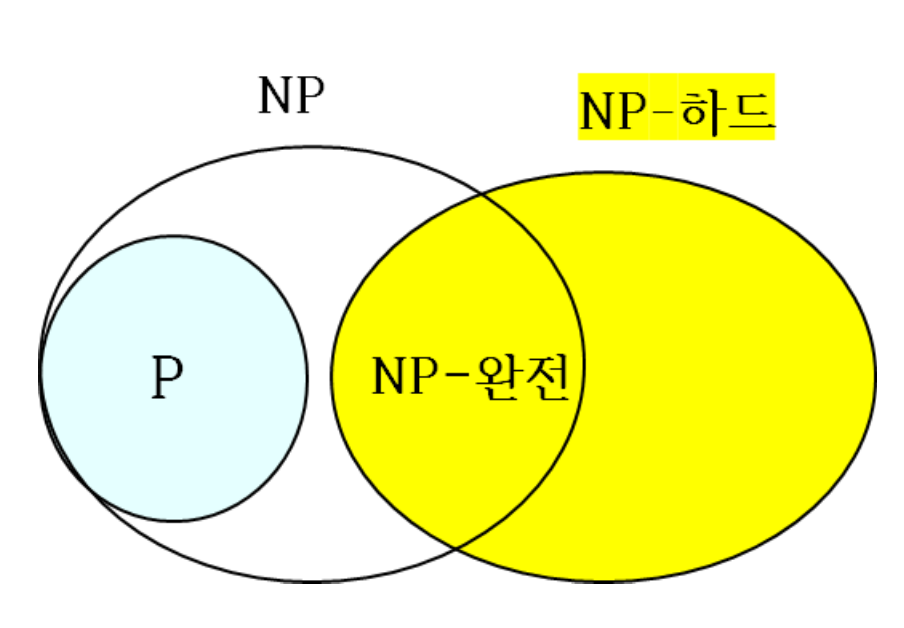
- A set of NP problems to which all NP probles reducible in polynomial time (solvable)
- Implication: the most inefficiently solved problems in NP
7.2.2 NP-Hard
- A set of problems to which all NP problems recudible in polynomial time
- Very difficult problem
- No need to be in NP
7.2.3 Reduction
- Reduction is a way of saying that one problem is "easier" than another
- We say that problem A is easier than B (i.e., we write "A B") if we can solve A using the algorithm that solves B
- Idea: transform the inputs of A to inputs of B

왜 A가 더 쉬울까? B를 풀 줄 알면 A도 공짜로 풀 수 있다고 치면 이해가 쉽다.
Polynomial Reductions
- Given two problems A, B, we say that A is polynomially reducible to B (A B) if:
- There exists a function that converts the input of A to inputs of B in polynomial time
- A(i) = YES B(f(i)) = YES
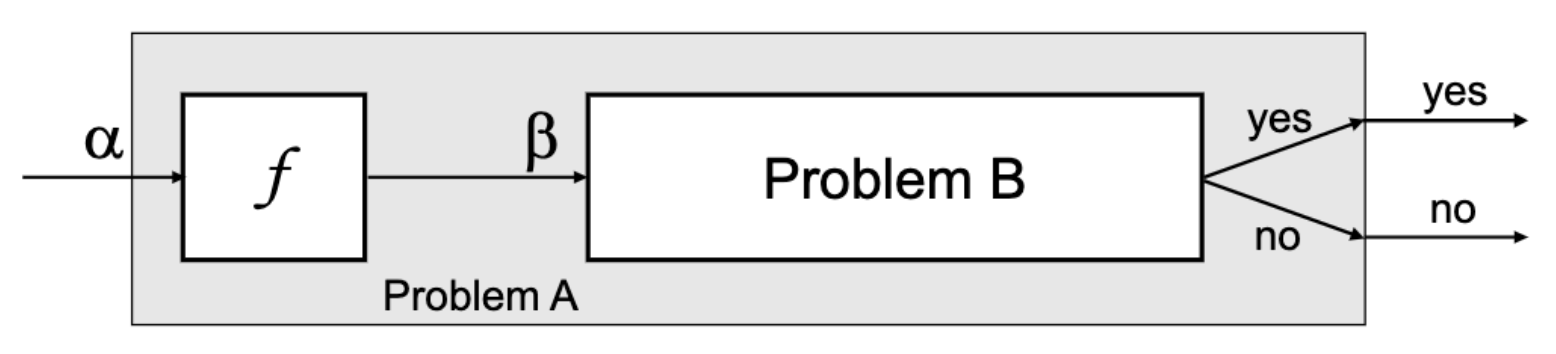
A B는 B를 결정할 수 있는 알고리즘이 하나만 있으면, f로 변환해서 그 알고리즘을 한 번 돌려서 A도 다항시간에 풀 수 있다는 말이다.
Implication of Reductions
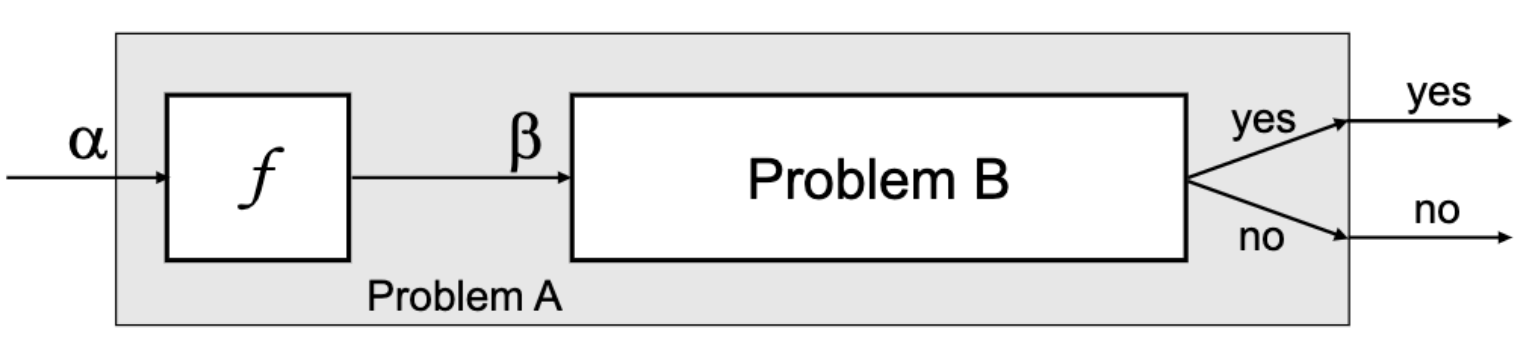
- If A B and B P, then A P
- If A B and A P, then B P
A 이면 B가 최소한 A만큼은 어렵다고 본다. 따라서 B가 P에 속해 쉽다면 그보다 같거다 덜 어려운 A도 P에 속한다. 같은 명제를 어려움 전달 관점에서 쓰면 A 이고 A가 P에 속하지 않는다고 알려져 있다면, B가 P에 속할 수 없다.
7.2.4 Reduction Example
- 문제 A = Subset Sum
- 정수의 집합 S의 부분 집합들 중에서 원소의 합이 K가 되는 부분 집합을 찾는 문제
- S = {20, 35, 45, 70, 80}이고, K = 105라면, {35, 70}의 원소는 합이 105가 되므로 문제의 해는 {35, 70}

이러한 경우는 직접 하나씩 해봐야 알 수 있기 때문에 brute-force
- 문제 B = Partition
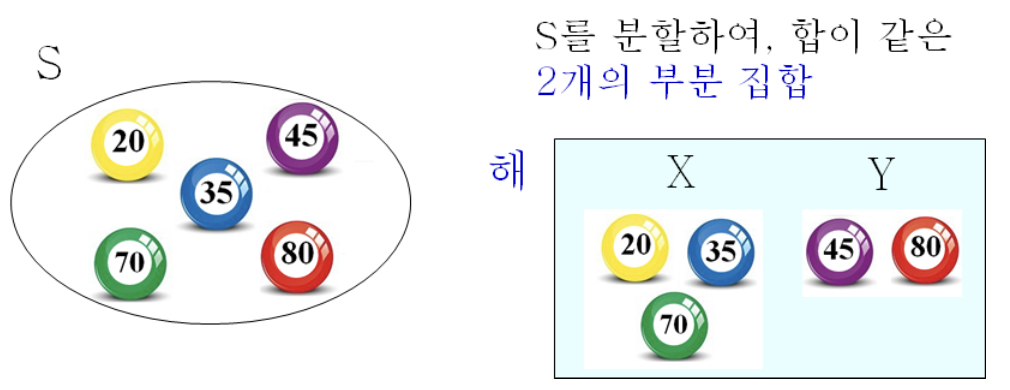
- 정수의 집합 S에 대해, S를 분할하여 원소들의 합이 같은 2개의 부분 집합을 찾는 문제
- S = {20, 35, 45, 70, 80}이고, X = {20, 35, 70}과 Y = {45, 80}이 해
- sum(X) = 20 + 35 + 70 = 125, sum(Y) = 45 + 80 = 125
7.2.5 Transition Idea
- 원래 문제: Subset Sum
- Partition으로 변환
- S 안의 모든 원소의 합을 s라고 두고, 새 원소 t = s - 2k 생성
- S에 t를 추가해서 새로운 집합 S' = S {t} 생성
- S'에 대해 "두 부분집합 X, Y로 나눠서 합이 같게 되나?"라는 partition 문제를 푼다고 생각한다.
- Partition 알고리즘이 해 X, Y를 찾았다고 하자.
- S' 전체 합은 s + t = s + (s - 2K) = 2s - 2K
- X와 Y의 합이 같으므로 각각 합은 절반인 s - K
- t가 들어있는 쪽에서 t만 빼면 Subset Sum의 해가 됨
- X와 Y 중 하나에 반드시 t가 들어있다. 그 집합을 X라고 하자.
- X의 합은 s - K, 여기서 t를 빼면 (s - K) - t = (s - K) - (s - 2K) = K
- 즉 X에서 t를 뺀 집합은 합이 정확히 K가 되는 부분집합이다.
E.g.,
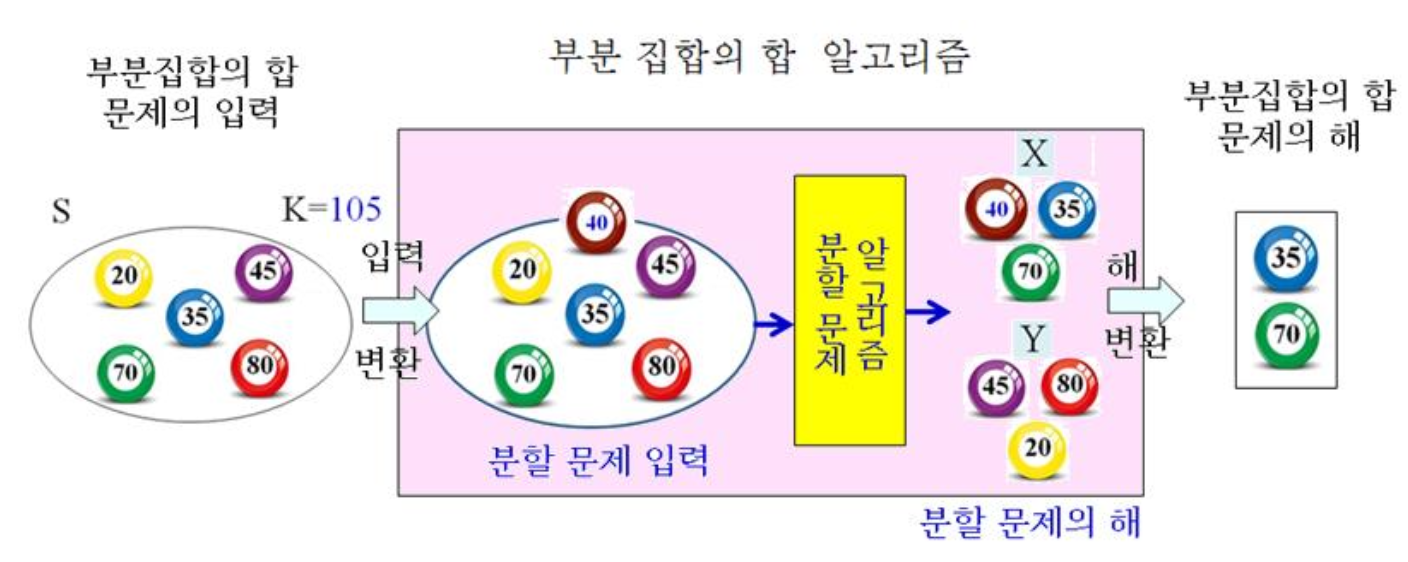
부분 집합의 합 문제를 분할 문제로 변환하여 해결하는 예제로 s, K, t 값은 다음과 같다.
- s = 20 + 35 + 45 + 70 + 80 = 250
- K = 105
- t = s - 2K = 250 - (2 105) = 250 - 210 = 40
NP-Complete
7.2.6 Time Complexity
- 문제를 변환하는 전 과정의 시간 복잡도는 다음의 3단계의 시간 복잡도의 합
- 문제 A의 입력을 문제 B의 입력으로 변환하는 시간
- 문제 B를 위한 알고리즘이 수행되는 시간
- 문제 B의 해를 문제 A의 해로 변환하는 시간
- 첫 단계와 세 번째 단계
- 단순한 입출력 변환이므로 다항식 시간에 수행
- 두 번째 단계
- 문제 변환의 시간 복잡도는 두 번째 단계의 시간 복잡도에 따라 결정
- 두 번째 단계가 다항식 시간이 걸리면, 문제 A도 다항식 시간에 해결

Why NP-Complete is important?
- If one NP-complete problem is solved in polynomial time
any NP-complete problem is solved in polynomial time - A complexity boundary
- P <= NP-Complete <= NP-Hard
어느 한 NP-Complete를 다항시간에 푸는 알고리즘을 찾으면, 그 문제로 환원되는 다른 모든 NP 문제도 연쇄적으로 다항시간에 풀 수 있다.
How to determine complexity of your problem?
- Polynomial verification
- given an input with size n, O(f(n)) need for verification
- A NP-complete problem is reducible to your problem in polynomial time
1 NP
1 & 2 NP-Complete
2 NP-Hard
Reduction of Ham-Cycle to TSP
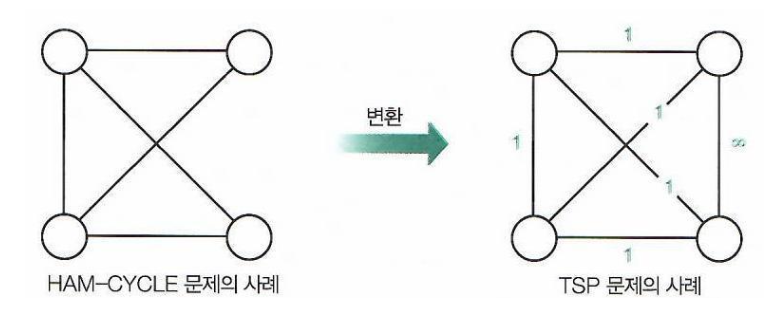
- Ham-Cycle has a cycle in the given case
TSP has a cycle with weight sum is length less that or equal to n (Ham-Cycle has no weight, but we can assign 1 equally) TSP is NP-Hard
G의 각 간선에 가중치 1을 부여해서 TSP 그래프로 보고, 원래 G에 없던 간선들은 사용하면 안 되게 아주 큰 비용으로 놓는다. TSP를 다항시간에 풀 수 있으면, 모든 NP 문제는 다항시간에 같이 풀려버린다.
Ham-Cycle TSP
7.3 NP-Completeness Problems
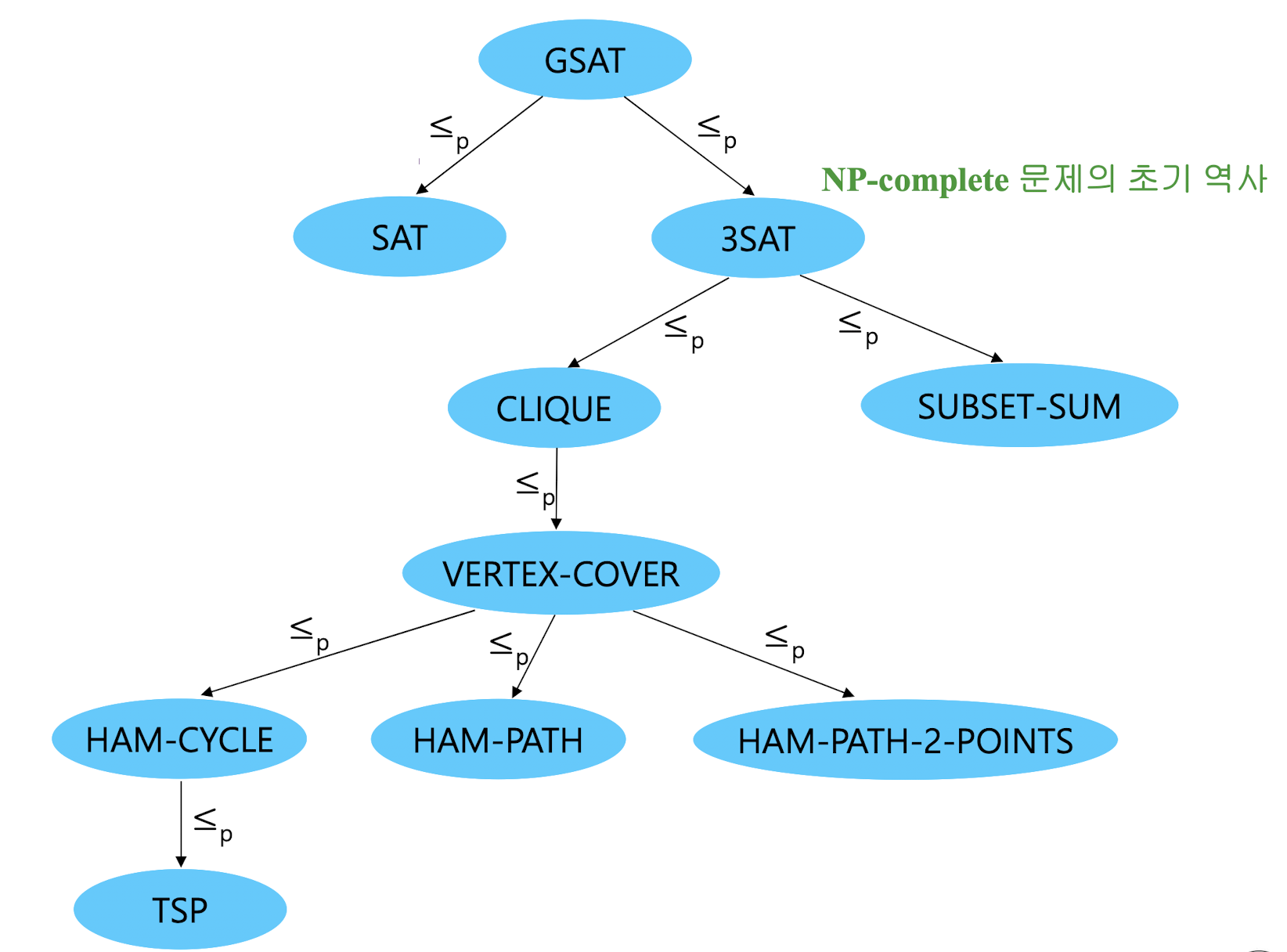
7.3.1 SAT
- Boolean variable들이 (OR)로 표현된 논리식이 여러 개 주어질 때, 이 논리식들을 모두 만족시키는 각 부울 변수의 값을 찾는 문제
E.g.,
- Boolean variable w, x, y, z에 대하여,

7.3.2 CNF-SAT
- CNF is a special case of SAT
- is in "Conjuctive Normal Form" (CNF)
- "AND" of expressions (i.e., clauses)
- Each clause contains only "OR"s of the variables and their complements
E.g.,
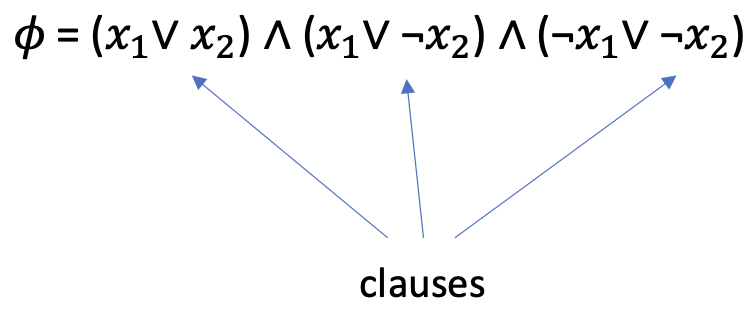
여러 개의 절이 AND로 되어 되어 있고, 각 절은 변수 또는 그 부정들을 OR로만 묶은 것이다.
7.3.3 Subset Sum
- 주어진 정수의 집합의 S의 원소는 합이 K가 되는 S의 부분 집합을 찾는 문제이다.
E.g.,
- S = {20, 30, 40, 80, 90}이고, 합이 200이 되는 부분 집합을 찾고자 할 때,
- Solution: {30, 80, 90}의 원소 합이 200이다.
7.3.4 Partition
- 주어진 정수의 집합의 S의 원소는 합이 K가 되는 S의 부분 집합을 찾는 문제이다.
E.g.,
- S = {20, 30, 40, 80, 90}일 때, S를 2개의 합이 동일한 부분 집합으로 분할하면,
- Solution: X = {20, 30, 80}, Y = {40, 90}; 각각의 부분 집합의 합이 130이다.
7.3.5 0-1 Knapsack
- 배낭의 용량이 C이고, 물건 각각의 무게와 가치가 와 일 때, 단 i = 1, 2, ...,n, 배낭에 담을 수 있는 물건의 최대 가치를 찾는 문제
- 단, 담을 물건의 무게의 합이 배낭의 용량을 초과하지 말아야 한다.
E.g.,
- C = 20kg, = 12kg, = 8kg, = 6kg, = 5kg이고, = 20, = 10, = 15, = 25
- Solution: 물건 2, 3, 4를 배낭에 담으면, 그 무게의 합은 8 + 6 + 5 = 19kg, 그 가치의 합은 10 + 15 + 25 = 50으로 최대
로 C가 n에 비해 매우 크면 real-time 처리가 어려울 수도 있다. C를 이진수 길이로 보면 거의 지수시간에 해당하기 때문에 이러한 알고리즘을 pseudo-polynomial time 알고리즘이라고 부른다. DP 알고리즘이 항상 빠른 알고리즘이 아니다.
7.3.6 Vertex Cover
- 주어진 그래프 G = (V,E)에서 각 간선의 양 끝점들 중에서 적어도 1개의 점을 포함하는 집합
- 최소 크기의 정점 커버를 찾는 문제
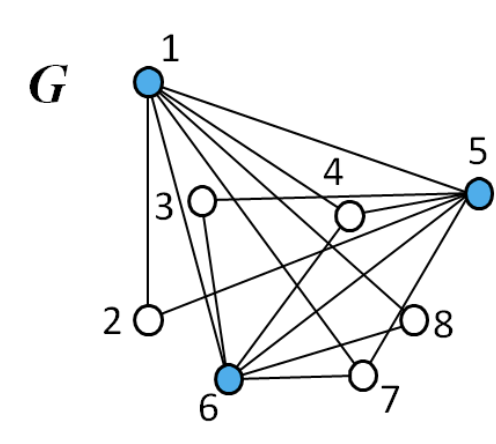
- Solution: {1, 5, 6} 그래프의 각 간선의 양 끝점들 중에서 적어도 1개의 끝점이 1, 5, 6 중에 하나이다. 그리고 이는 최소 크기의 커버
Set Cover처럼 간단한 Greedy로 풀면 일반적으로 최적 해가 보장되지 않는다. 정확한 해를 얻으려면 지수 시간급 탐색(전수조사)이 필요하다.
7.3.7 Independence Set
- 주어진 그래프 G = (V, E)에서 연결하는 간선이 없는 점들의 집합
- 최대 크기의 독립 집합을 찾는 문제
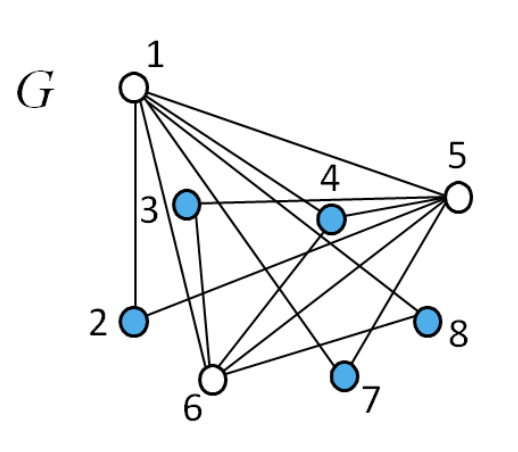
- Solution: {2, 3, 4, 7, 8}은 서로 간선으로 연결 안 된 최대 크기의 독립 집합
7.3.8 Clique
- 주어진 그래프 G = (V, E)에서 모든 점들 사이를 연결하는 간선이 있는 부분 그래프
- 최대 크기의 클리크를 찾는 문제
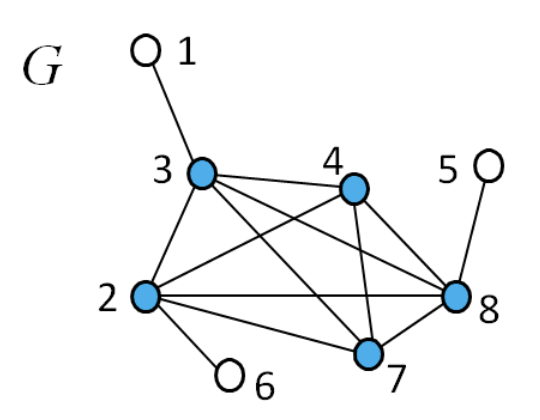
- Solution: {2, 3, 4, 7, 8}은 서로 간선으로 모두 연결된 최대 크기의 클리크
7.3.9 Graph Coloring
- 주어진 그래프 G = (V, E)에서 인접한 점들을 서로 다른 색으로 색칠하는 것
- 가장 적은 수의 색을 사용하여 그래프를 색칠하는 문제
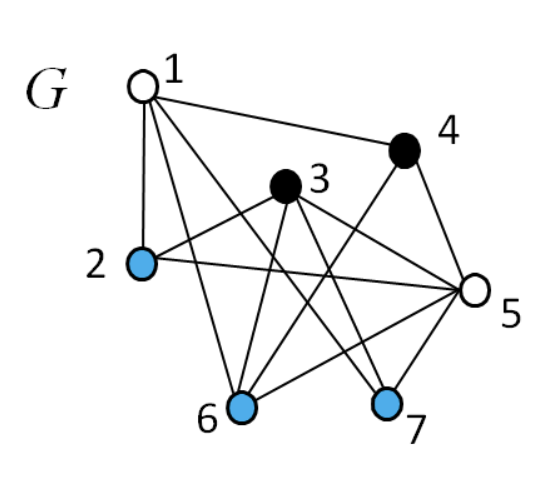
- Solution: {1, 5}는 흰색, {3, 4}는 검은색, {2,6, 7}은 파란색으로 칠한다.
3가지 색보다 적은 수의 색으로 이 그래프를 칠할 수는 없다.
7.3.10 Set Cover
- 주어진 집합 S = {1, 2, 3, ... , n}에 대해서 S의 부분 집합들이 주어질 때, 이 부분 집합들 중에서 합집합하여 S와 같게 되는 부분 집합들을 집합 커버라고 한다.
- 집합 커버 문제는 가장 적은 수의 부분 집합으로 이루어진 집합 커버를 찾는 문제
E.g.,
- S = {1, 2, 3, 4, 5}, 부분 집합: {1, 2, 3}, {2, 3, 4}, {3, 5}, {3, 4, 5}라면,
- Solution: {1, 2, 3}과 {3, 4, 5}를 합집합하면서 S가 되고, 부분 집합 수가 최소이다.
7.3.11 Longest Path
- 주어진 가중치 그래프 G = (V, E)에서 시작점 s에서 도착지 t까지의 가장 긴 경로를 찾는 문제
- 단, 간선의 가중치는 양수이고, 찾는 경로에서 반복되는 점이 없어야 한다.
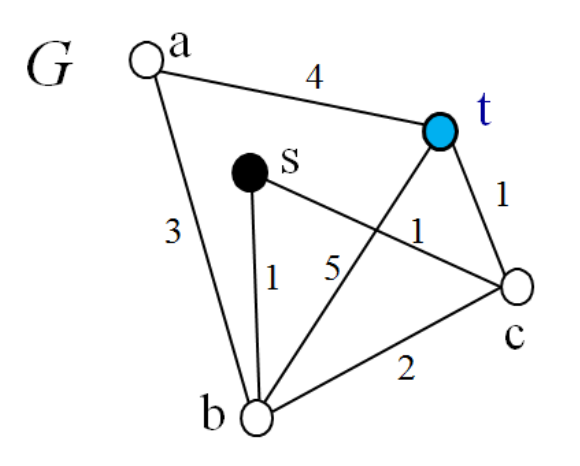
- s -> c -> b -> a -> t가 최장 경로로 길이는 10이다.
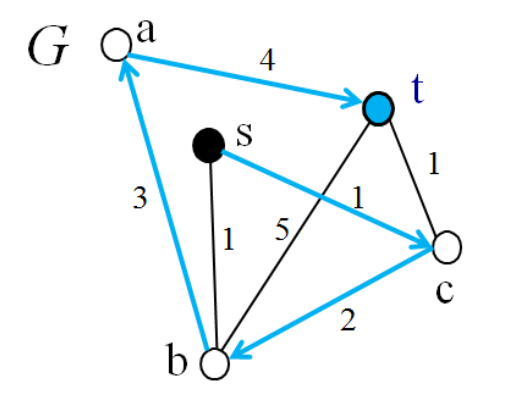
Shortest path는 한 번 경로를 선택하면 길이가 더 줄어들 여지가 없어 "확정된 최단 거리"가 되지만, Longest path는 어떤 경로를 골라도 더 긴 경로가 존재할 수 있다.
7.3.12 Traveling Salesman
- 주어진 가중치 그래프 G = (V, E)에서, 임의의 한 점에서 출발하여 다른 모든 점들을 1번씩만 방문하고, 다시 시작점으로 돌아오는 경로 중에서 최단 경로를 찾는 문제
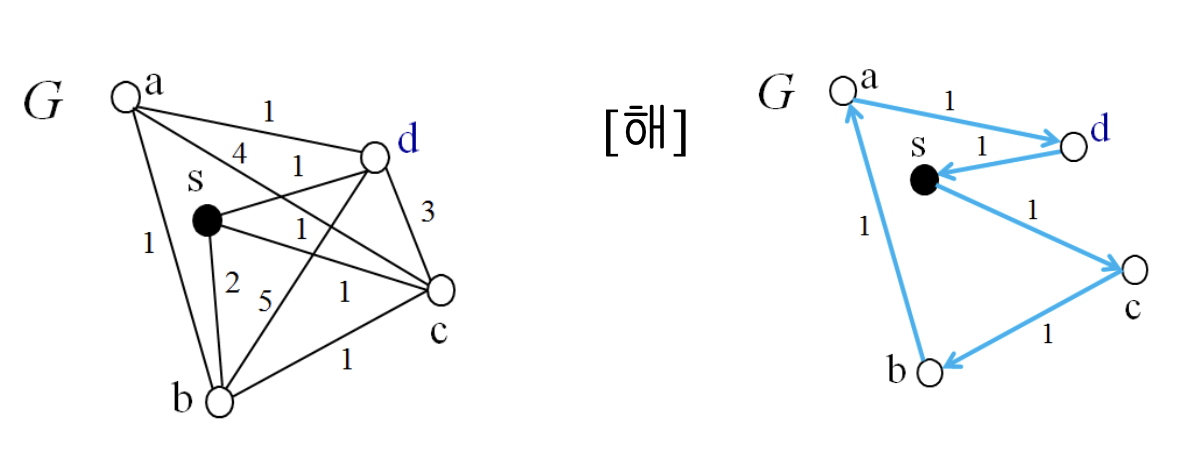
7.3.13 Hamiltoniam Cycle
- 주어진 그래프 G = (V, E)에서, 임의의 한 점에서 출발하여 모든 다른 점들을 1번씩만 방문하고 다시 시작점으로 돌아오는 경로를 찾는 문제
- 간선의 가중치를 모두 동일하게 하여 TSP 문제의 해를 찾았을 때, 그 해가 hamiltonian cycle 문제의 해가 된다.
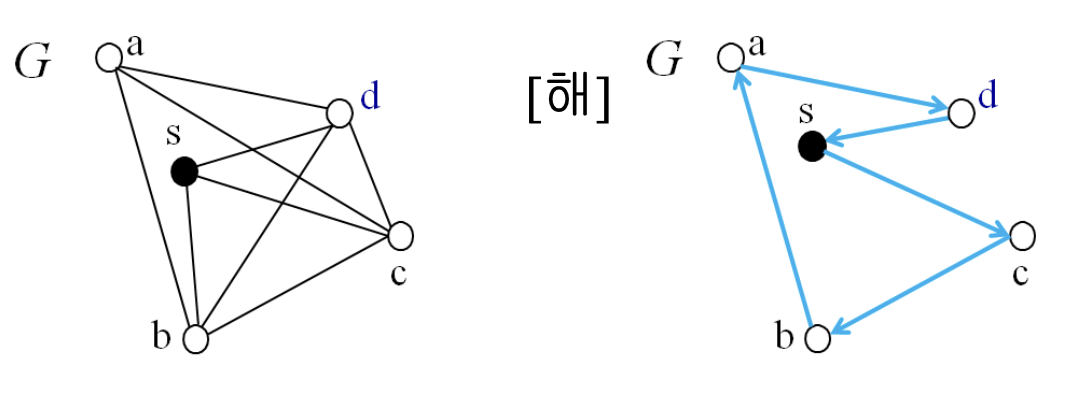
7.3.14 Bin Packing
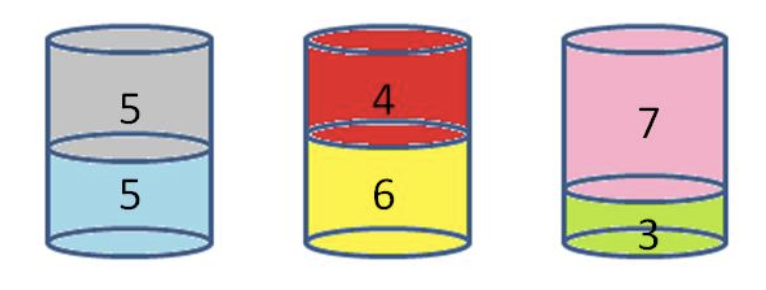
- n개의 물건이 주어지고, 통의 용량이 C일 때, 가장 적은 수의 통을 사용하여 모든 물건을 통에 채우는 문제
- 단, 각 물건의 크기는 C보다 크지 않다.
E.g.,
- 통의 용량 C = 10이고, n = 6개의 물건의 크기가 각각 5, 6, 3, 7, 5, 4
- Solution: 3개의 통을 사용하여 아래와 같이 채울 수 있다.
7.3.15 Job Scheduling
- 각 작업의 수행 시간 , 단 i = 1, 2, 3, ..., n, 그리고 m개의 동일한 성능의 기계가 주어질 때, 모든 작업이 가장 빨리 종료되도록 작업을 기게에 배정하는 문제
E.g.,
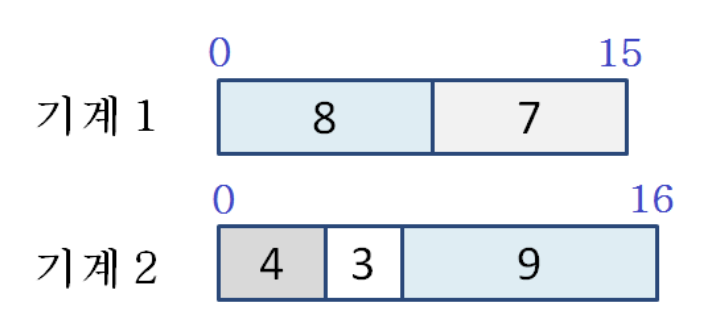
- n = 5개의 작업이 주어지고, 각각의 수행 시간이 8, 4, 3, 7, 9이며 m = 2
- Solution: 아래와 같이 작업을 배정하면 가장 빨리 모든 작업 종료
7.4 Application
SAT
- Formal Verification
Subset Sum
- Password 검사 및 메시지 검증
Partition
- Network Design
- Pattern Recognition
- Circuit Design
- VLSI Design
0-1 Knapsack
- 원자재 버리는 부분을 최소화하는 분할
Vertex Cover
- Boolean Logic Minimization
- Network Flow
Set Cover
- City Planning에서 공공 기관 배치
- Computer Virus 찾기
Independent Set
- Computer Vision
Clique
- 단백질 특성 연구
Longest Path, TSP, Hamiltonian Cycle
- Vehicle Rounting
Job Scheduling
- 항공 산업에서 공항 gate scheduling