8. Approximation Algorithm (2)

8.4 Task Scheduling

Goal

• Minimize the time of running all tasks

Condition

• N tasks given
• T = {$t_i$ | $t_i$ = required time to finish task i, i = 1, 2, 3, ... , n}
• M machines
• After a job is assigned to a machine, we can not change the machine in its running time
• If a machine is running for a job, we can not assign another job

Greedy Search에서는 각 작업의 시작 시간과 종료 시간만 주어지고 사용 가능한 기계수의 제한이 없었다.
반면 근사 알고리즘에서는 전체 작업 수와 사용할 수 있는 기계 수가 미리 정해져 있고 각 작업의 처리 시간이 주어졌을 때 모든 작업을 수행하는 스케줄 중에서 전체 완료 시간이 가장 짧은 해를 목표로 한다.

Greedy Algorithm for Task Scheduling

• Different from what we covered in the greedy algorithm chapter
• Early ending machine first

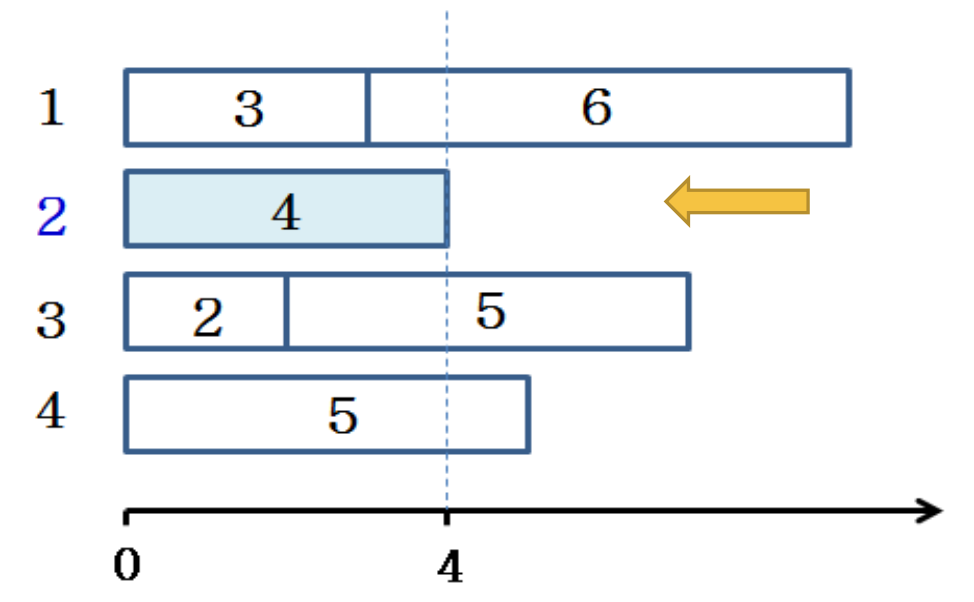
절대 시간 4를 기준으로 하면 제일 빨리 끝나는 게 2번 기계이다. 같은 시간이면 여러 개 중에서 앞에서부터 채운다.

8.4.1 Approx_JobScheduling(T, M)

• Input: n tasks, task $t_i$, i = 1, 2, ..., n, machine $M_j$, j = 1, 2, ... , m
• Output: the ending time of finishing all tasks

E.g.,

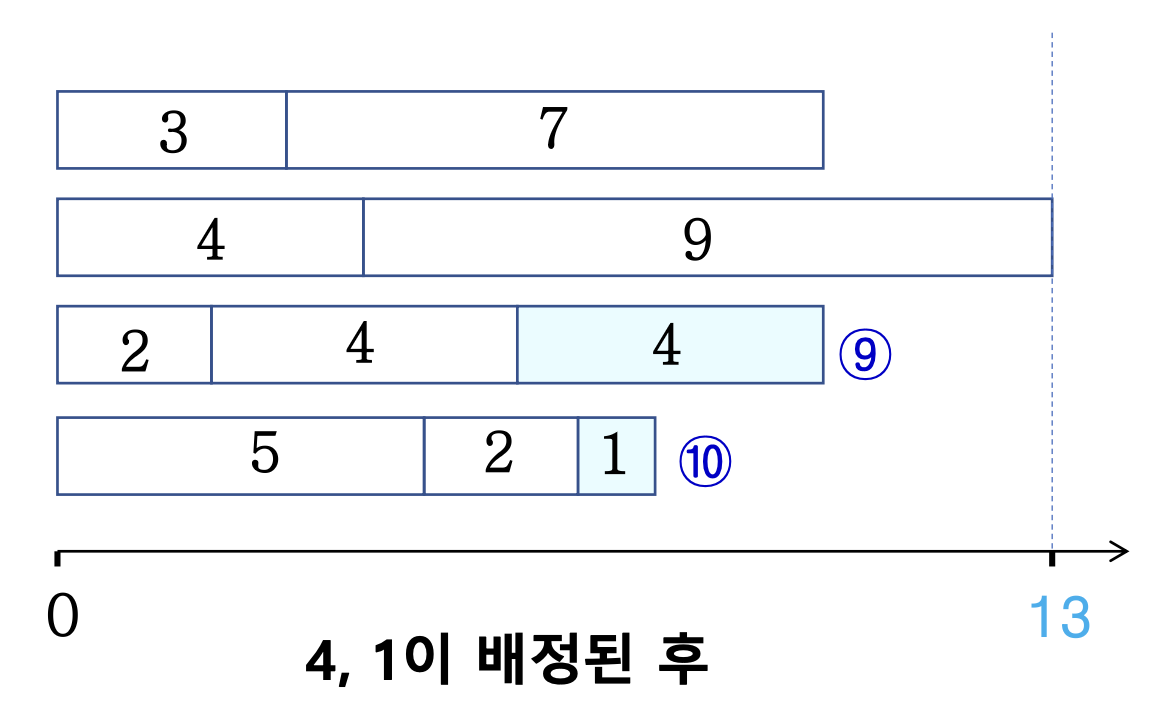
• T = {5, 2, 4, 3, 4, 7, 9, 2, 4, 1}
• 4 machines

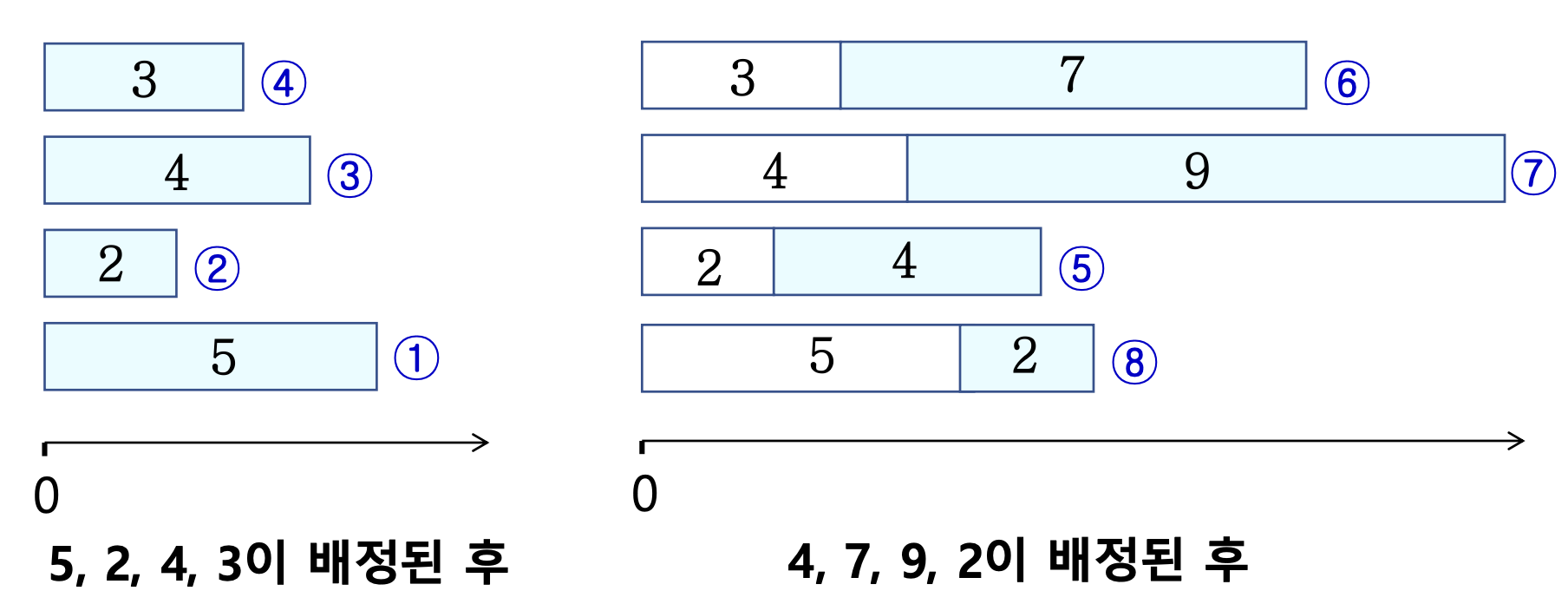
• Finishing time: 13

8.4.2 Approximation Ratio

Theorem 1: OPT'/OPT < 2

• OPT': approximation by Approx_JobScheduling
• OPT: optimal solution

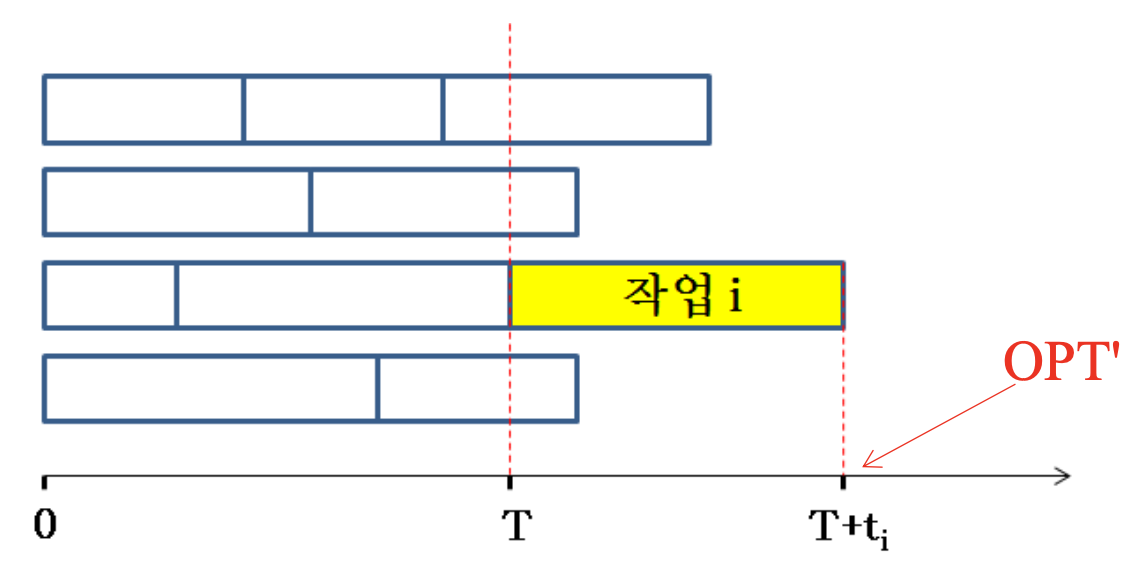
T + t' = OPT'
m: Machine size

Lemma 1: T <= T'

• T = OPT' - $t_i$
• M = T + E[ending time of all machine - T]
  • = total task running time / m $\rightarrow$ lower bound
  • T 기준으로 앞을 다 빼고난 뒤에서의 평균
• T' = T + E[ending times except the machine running $t_i$ - T]
  • = M - $t_i$ / m
• The expectation for T' is positive or 0, so T <= T'

Lemma 2: M <= OPT

• M = T + E[ending time of all machine - T]
  = total task running time / m
• OPT is the earliest ending time of the latest ending time in machines
• Ending time of each machine < OPT
• If M(lower bound) > OPT
  • OPT >= E[ending time of all machine] $\rightarrow$ contradiction

contradiction: 이게 성립하면 모순이 생긴다.

Lemma 3: $t_i$ <= OPT

• No doubt
• OPT should max($t_i$) by definition

OPT가 하나의 task보다 작을 수는 없다.

최악의 경우 2배까지 느려질 수 있다.

---

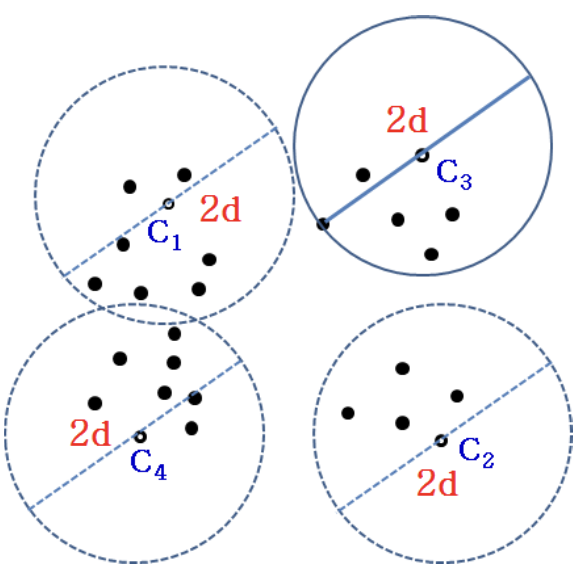
8.5 Clustering

• Grouping similar data regard as a type of data (cluster)
• Modeling
• What data is in which type? - find the closet cluster

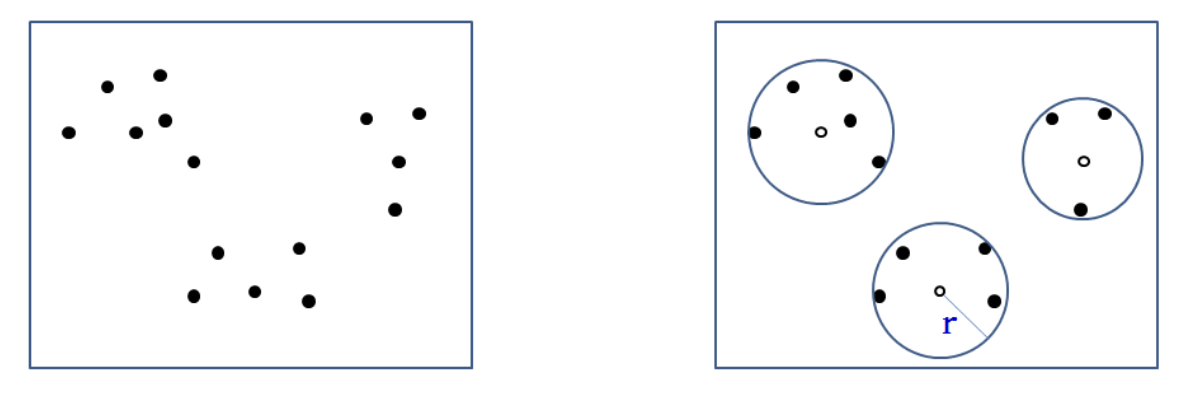
How to Determine a Cluster?

• Minimize the expected distance of data points to the centroid of their cluster
• Find the expected minimum radius of k-clusters to cover all data

반경을 작게 잡을수록 정확도가 올라간다.

• In 2D space, find k clusters
• E.g., k = 3

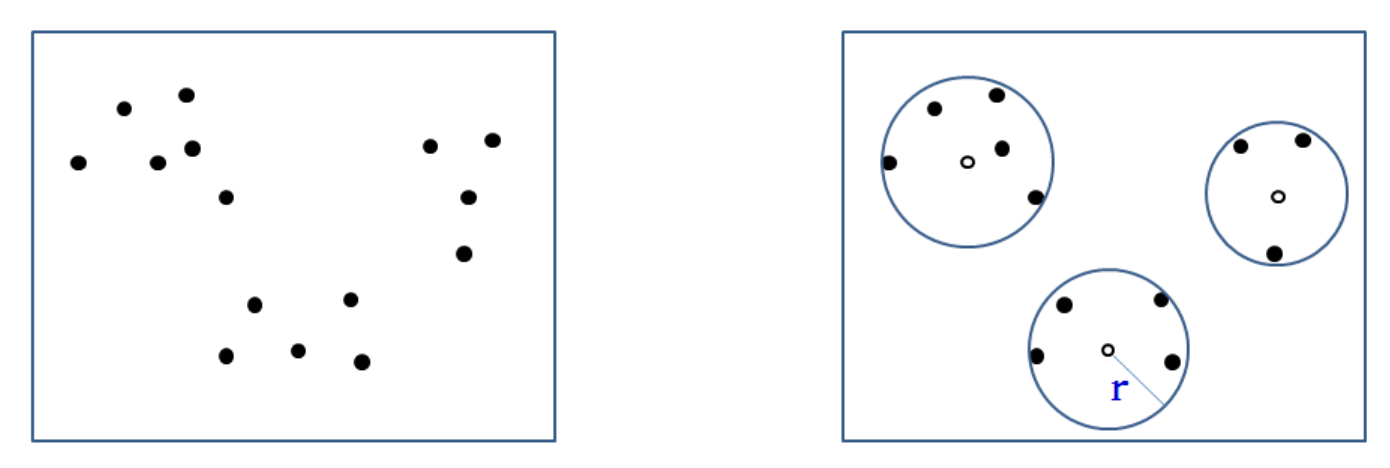
위 상황에서 new data를 넣는다면 1, 2, 3 cluster group 중에 어디로 가야할까?

8.5.1 Greedy Algorithm of Clustering

• Select one by one and determine its cluster at each iteration

How to select next one?

• Find the closet one and assign it to the same cluster until the radius is larger than a threshold
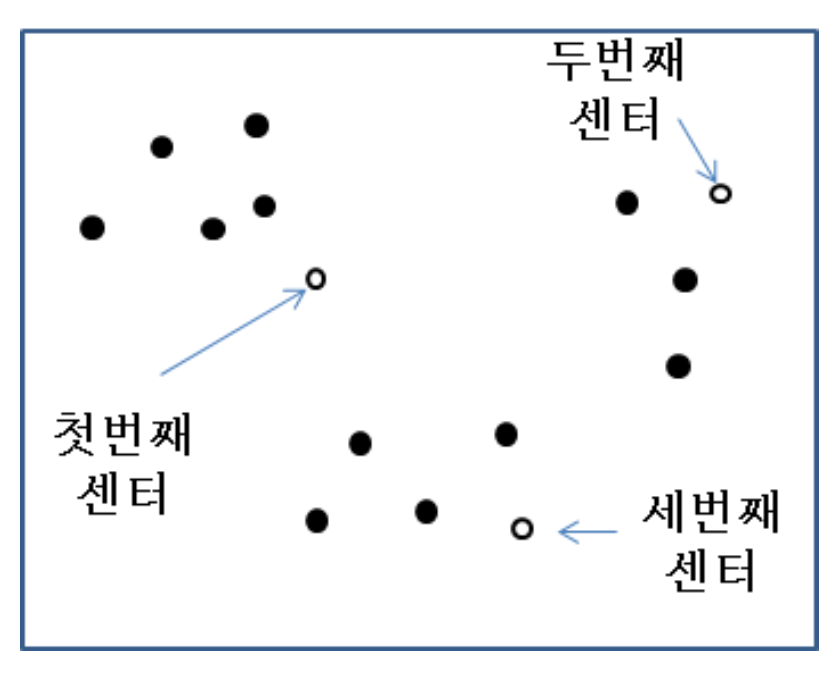
• Or find the furthest point and assign to a different cluster

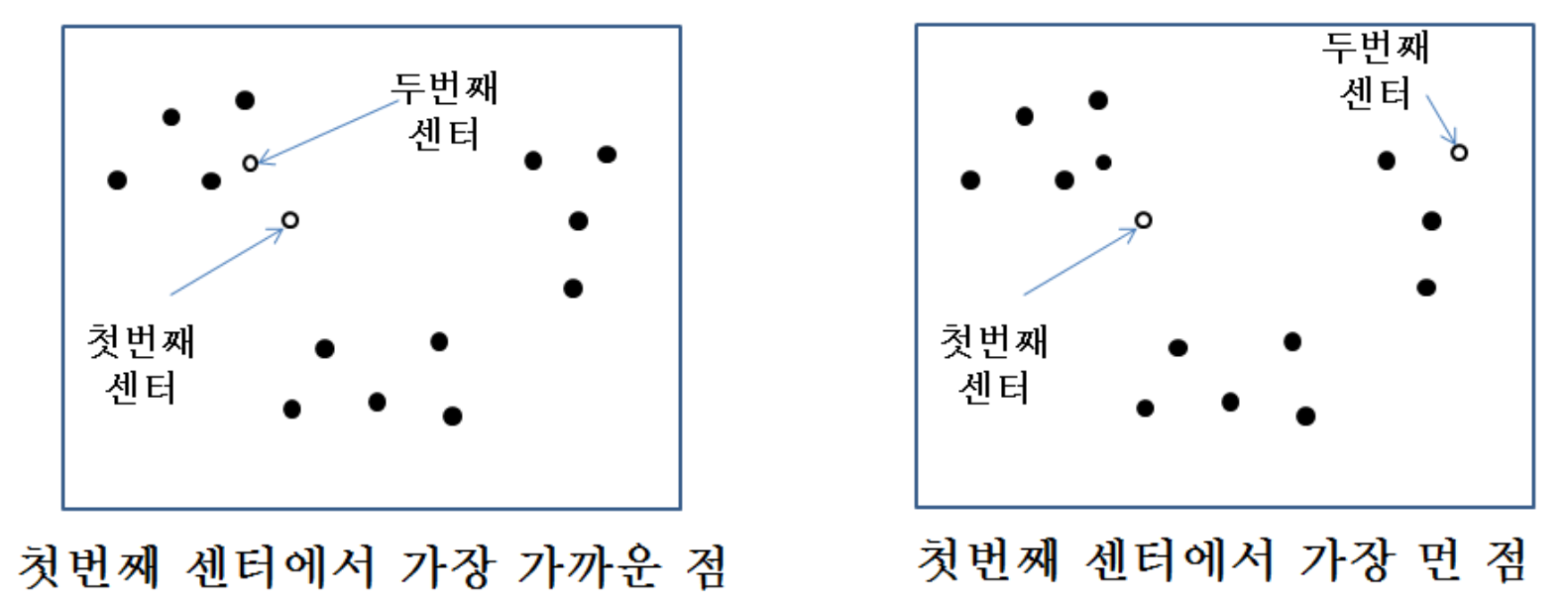
첫 번째 센터를 정할 때는 완전한 random이지만, 두 번째 센터는 첫 번째로부터 가장 먼 점을 선택한다.

Next?

• The furthest point from selected two points

8.5.2 Approx_k_Clusters()

• Input: 2D n vectors $x_i$,. i = 0, 1, ... , n-1, cluster size k, k > 1
• Output: k centroid and cluster arrangement for all points

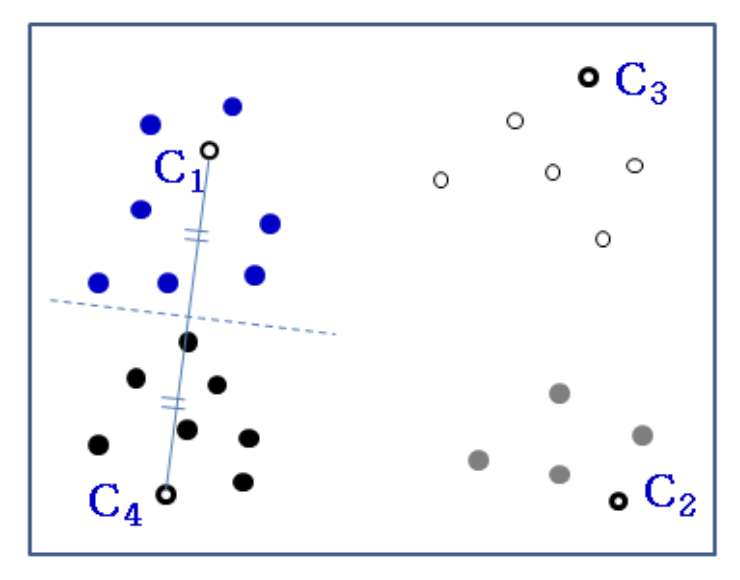
E.g., k = 4

1. Random selection of centroid of $C_1$

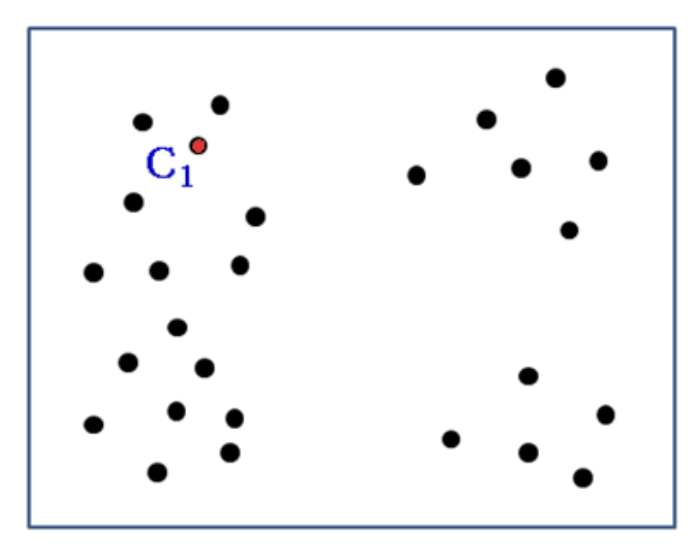
2. Evaluate distance of all points from $C_1$ & Select the furthest one as $C_2$

3. Let's assume that maximum of minimum distance was 20 $\rightarrow$ $C_3$ is selected

min 중에서 최댓값을 선택하면 $C_3$

4. $C_3$ is selected

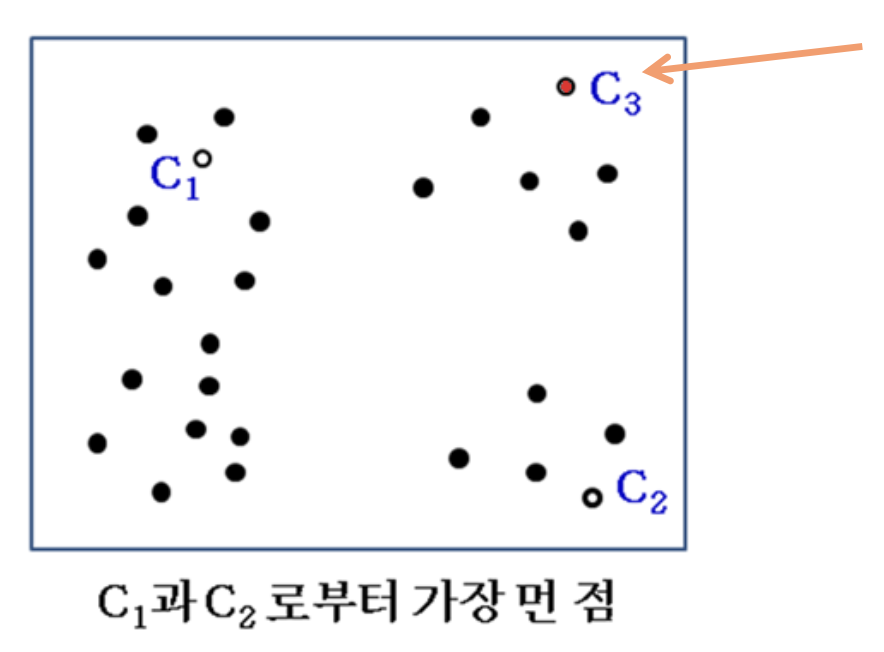
5. In the same way, we can select $C_4$

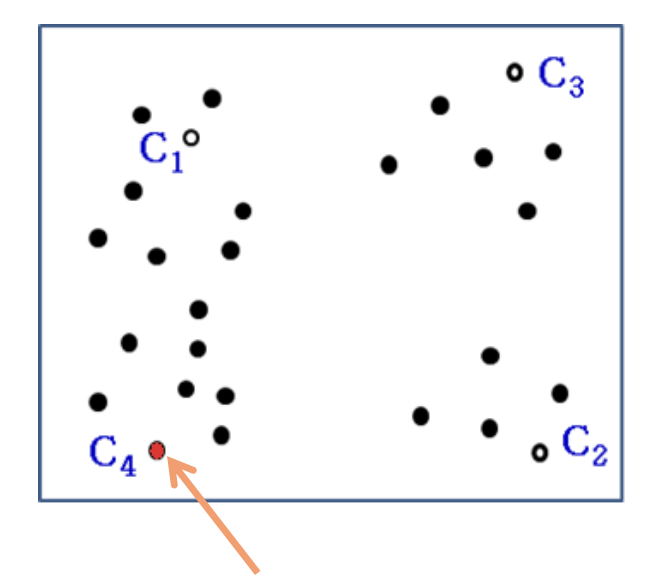
6. Evaluate distance of $x_i$ to $C_1 ~ C_4$
7. Find the closet cluster
8. Assign $x_i$ to the cluster

8.5.3 Time Complexity

• 3~5 line의 outer loop => $O(k)$
• Inner1: $O(n)$ - i = 0 to n - 1
• Inner2: $O(k)$ - all j니까 최악의 경우 k
• Total: $O(nk^2)$

8.5.4 Quality of a Solution

• Min-Max Distance: max(d($x_i$, $c_j$)) over all i where j = argmin$_k$d($x_i$, $c_k$)
• M': Minimal min-max distance (optimal)
• M: A lower bound of M'
• M": Approximated max-min distance; 근사 알고리즘으로 구한 값

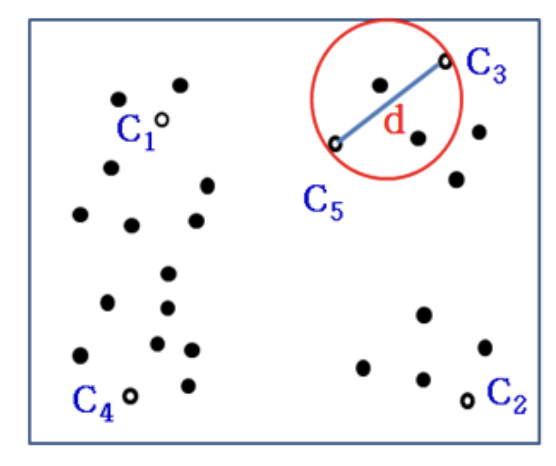
Lemma 1: 2M' >= d

• d = d(C[k], C[k+1]) = max$_i$(min$_j$(d($x_i$, C[j]))
• Select k + 1 centroids through the greedy algorithm
• Any algorithm should put two of the centroids into one cluster
• A cluster in an optimal solution should have large diameter than d
• M': max(all radius of k clusters)
• 2M' >= d

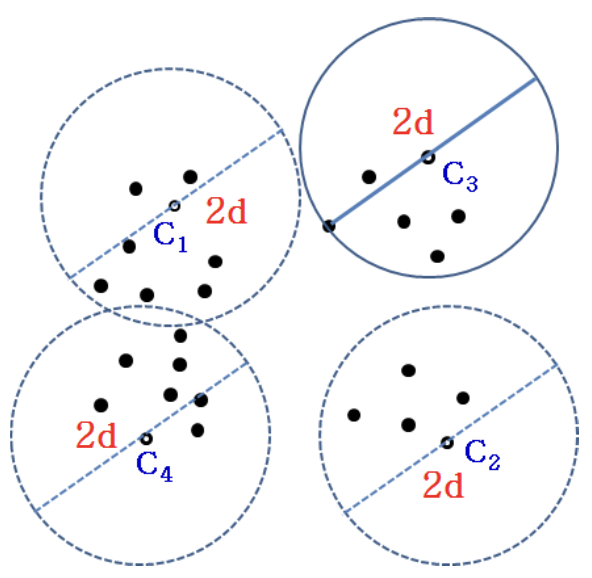
Lemma 2: M" <= d

• Any $x_i$ has shorter distance to its closest cluster
• = d($x_i$, C[j]), $x_i$ is assigned to C[j]
• Therefore, any cluster has a radius smaller than or equal to d

Theorem 1: M" / M' <= 2

• 2M' >= d (by lemma 1)
• M" < d (by lemma 2)
• M" / M' <= 2