9. Search Algorithm(2)

9.3 Simulated Annealing

Branch-and-Bound

• Find the probable solution first
• If we find a solution, go to the next probable "state" $\rightarrow$ a partial solution

항상 부분해들을 체계적으로 탐색하고 bound를 pruning하여 정확한 최적해를 보장한다.

Simulated Annealing

• Find a complete candidate solution
• If it is not good enough, change some components to go the another "state"
• Assumption: current solution with a minor change its quality so much

항상 완전한 해 하나를 들고 다니면서, 조금씩 변형해 가며 좋은 해를 찾는 확률적 최적화 기법이다.

Search solutions near currently observed good solutions

Branch-and-Bound quality가 나쁜 상태는 중간 단계에서 pruning하고 다시는 탐색하지 않는다. 반대로 SA는 해를 완전히 제거하지 않고 현재 해를 조금씩 변경하면서 주변 해 공간을 계속 탐색한다.

• If quality is bad $\rightarrow$ large change
• If quality is good $\rightarrow$ small change

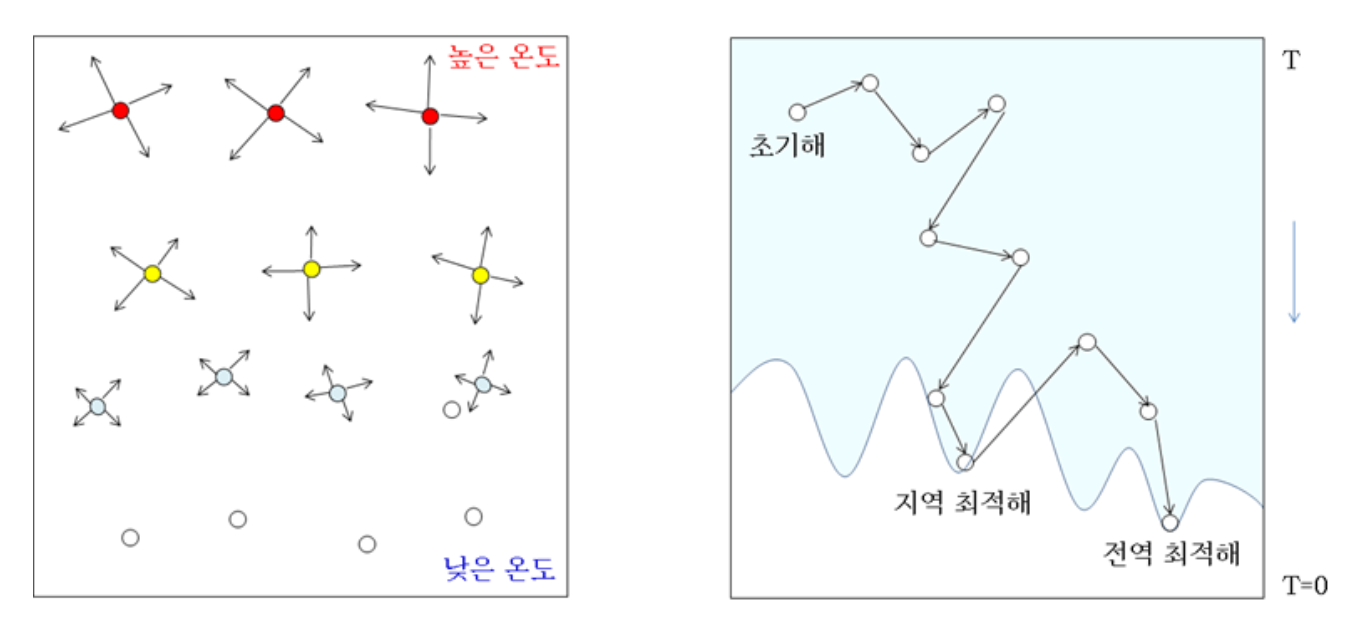
온도 T가 높을 때는 큰 변화도 자주 허용하므로 해가 크게 요동치며 전역 탐색을 시도한다.

• Criterion
• How much change is required for how good solutions?
  • Unclear
• An approach
  • Control by temperature

9.3.1 SimulatedAnnealing()

• S: 모든 정점을 한 번씩 방문해 이루어진 하나의 cycle
• T: 온도

d가 0 이상(같거나 더 나쁜 해)일 때도, 난수 $q \in (0,1)$와 비교해 q < p이면 그 해로 이동하도록 하여 나쁜 해를 확률적으로 가끔 받아들인다.

• Cooling rate $\alpha$
  • $T \leftarrow \alpha T$, 온도가 감소하는 속도 결정
  • $\alpha$가 1에 가까울수록 온도가 천천히 줄어들어 이웃으로의 이동 오래 유지되고 탐색 강해짐
  • $\alpha$ 작을수록 온도가 빨리 식어 이웃 이동이 빨리 제한되고, 탐색 범위가 좁아짐
• Make movement to a neighbor slow
• Affect exploration strength

• Probability of selecting a randomly generated neighbor p
• $p = 1 /e^{d/T} = e^{-d/T}$
  • 초기에는 $T$가 커서 $p$가 크므로 나쁜 해도 비교적 자유롭게 받아들여 다양한 $s$를 탐색할 수 있다.
  • $d$가 클수록(해가 많이 나빠질수록) $p$는 작아지지만, 0이 되지는 않으므로 지역 최적해에 갇혀도 탈출 가능성이 존재한다.
• Large T $\rightarrow$ high probability to accept a neighbor
• Small T $\rightarrow$ low probability to accept a neighbor

9.3.2 Pre-defined operators for TSP

• How to generate a neighbor?
• Use pre-defined operators (for TSP)
  • Insertion
  • Switching
  • Inversion

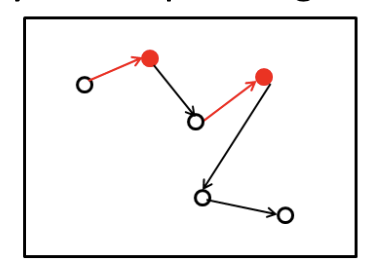
1. Insertion

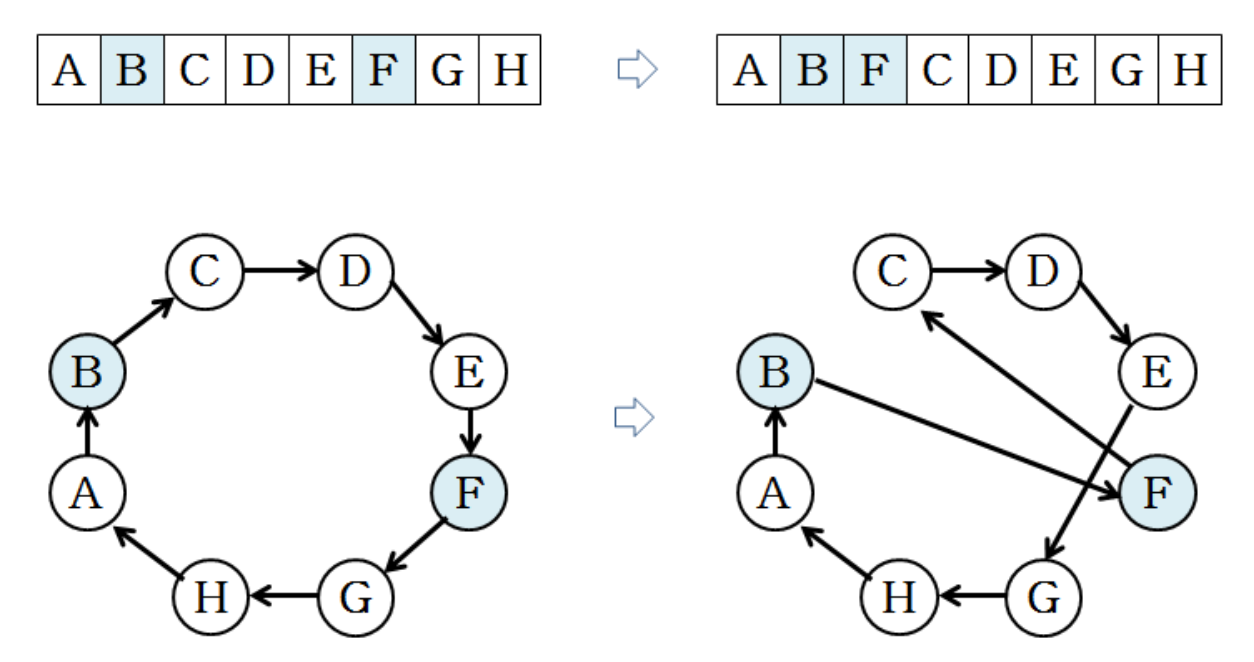
2. Switching

• 2번의 insertion과 같지만 insertion보다 많은 path의 변화를 일으킨다.

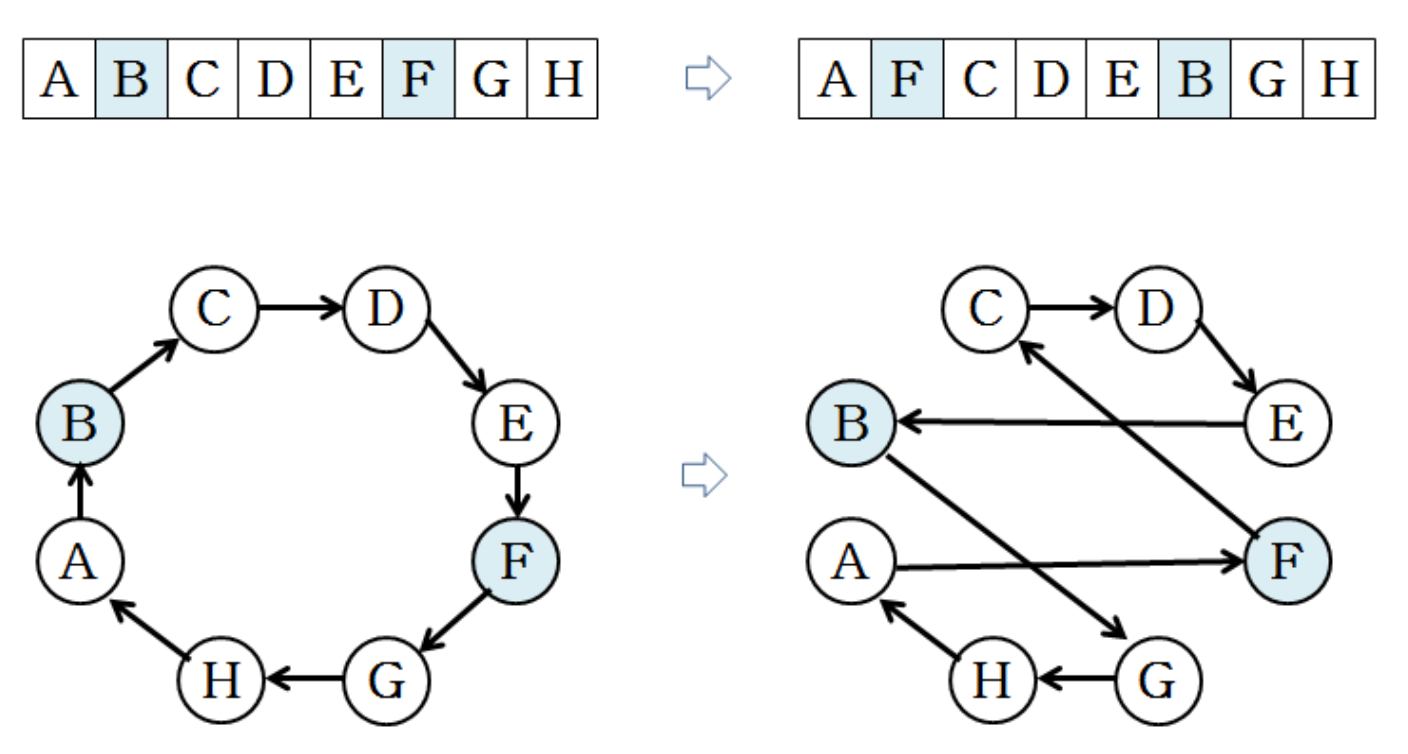
3. Inversion

---

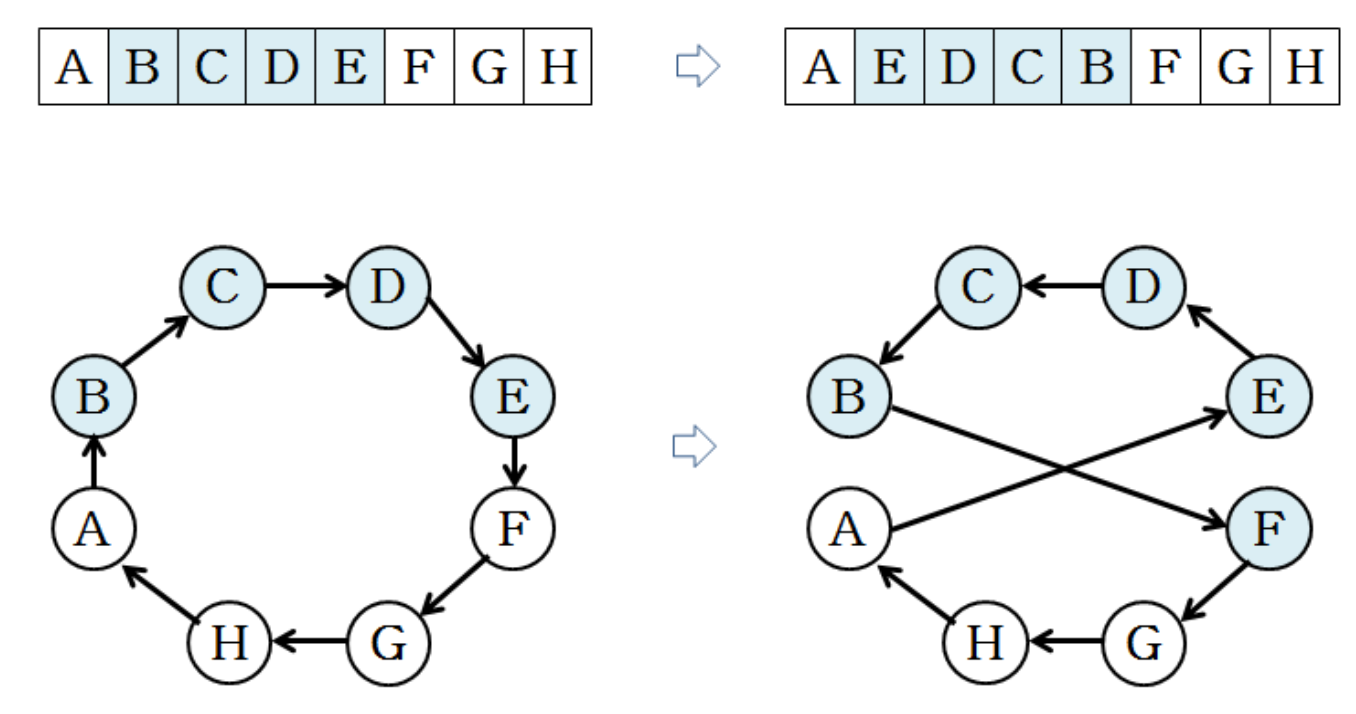
9.4 Genetic Algorithm

Simulated Annealing

• Improve an observed solution
• Determine the next search subspace by the best in the observed samples

좋은 해 하나를 계속 변형하며 탐색하는 알고리즘

Idea of Genetic Algorithm

• Why not improve many samples?
• They may have a good combination for optimal solutions (building block)
• If we can re-combinate the building blocks $\rightarrow$ an optimal solution

좋은 부분 구조를 가진 해들을 여러 개 유지하고, 그 사이에서 교차와 돌연변이 같은 연산으로 모의 담금질처럼 변형을 주되 집단 전체를 진화시키는 방법

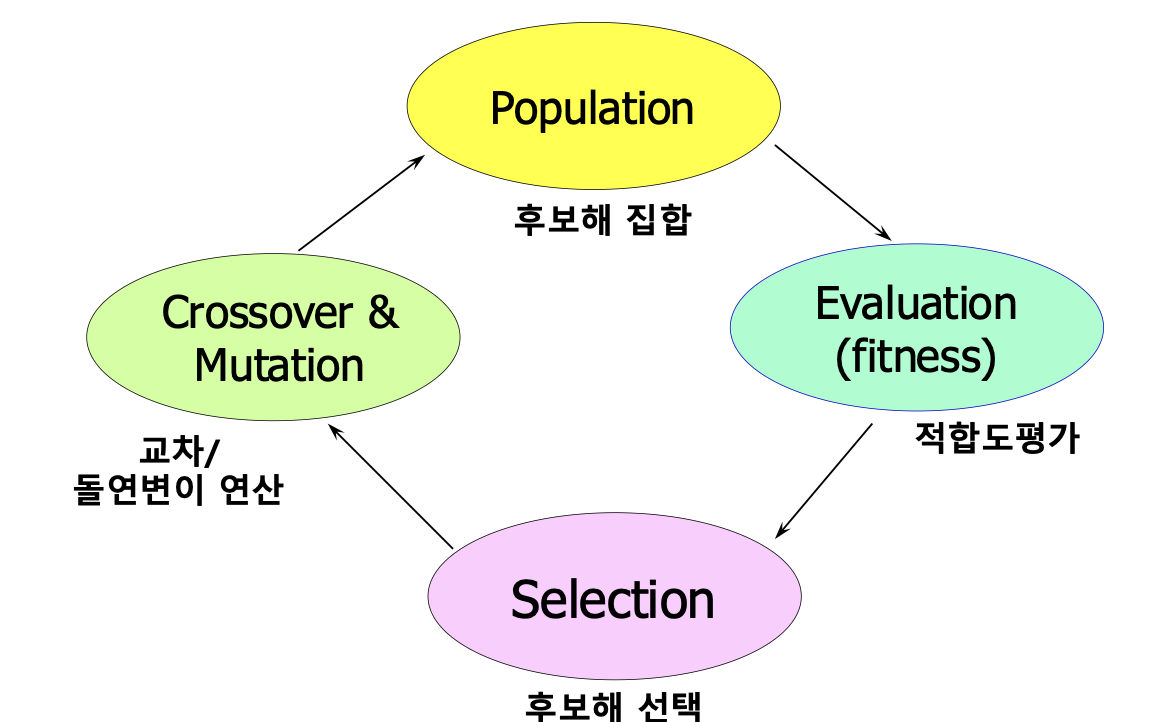
9.4.1 Genetic()

• The simplest from of GA
• G: 세대 t에서의 population
  • 개체: population 안에 들어있는 한 개의 해

• Evaluate individuals in $G_{t+1}$
  • 각 개체의 fitness를 계산해 평가
  • 이 값을 기준으로 좋은 해/나쁜 해를 구분하고 선택, 교차 확률 등에 사용한다.

E.g.,

• TSP: G = {A, B, C, D, E}, stating node = A
• Examples of candidate solutions: ABCDEA, ACDEBA, AECDBA, ...

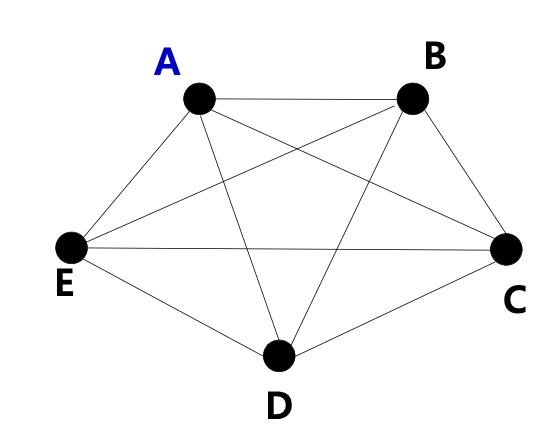
Search Space

• Permutation of 5 nodes = 5! = 120
• (n-1)! for n vertices = (5-1)! = 4! = 24

9.4.2 Fitness Definition

• Fitness = Target objective to optimize
• TSP: minimum weight sum
• Fitness Function(a candidate solution) = weight sum of used edges
• f(ABCDEA) = 5 + 2 + 1 + 3 + 9 = 20

Basic Operator

• Selection
• Crossover
• Mutation
• .. many other operators exist

1. Selection

• Determines which individuals will be "selected" for the next generation
• Issues
  • How many individuals?
  • How good individuals?
  • How diverse individuals?
  • Elitism

Roulette Wheel Selection

• The simplest selection method
• Probability is assigned by fitness
• Probability of selecting sample A
  • f(A) / sum(f(i) for all i)
• Issues
  • Relative ratio
  • Absolute ratio
  • Adaptive ratio

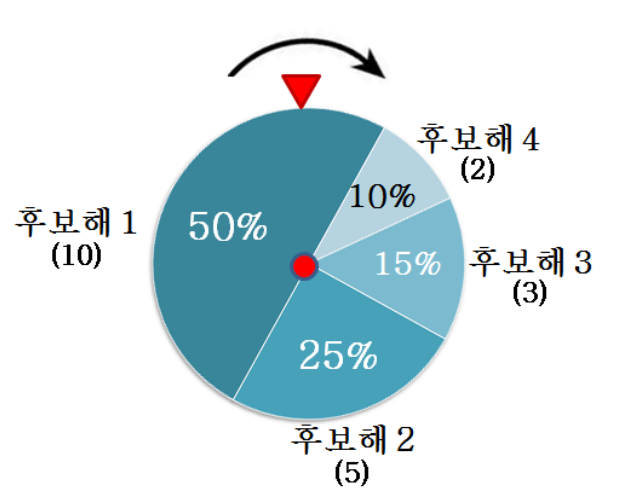
• Evaluate a multinomial distribution
• Repeat sampling
• Issue
  • Duplicated sampling
  • Others: Tournament Selection, ...

2. Crossover

• A process to compose building blocks
• One-point crossover
• $\leftrightarrow$ two-point crossover

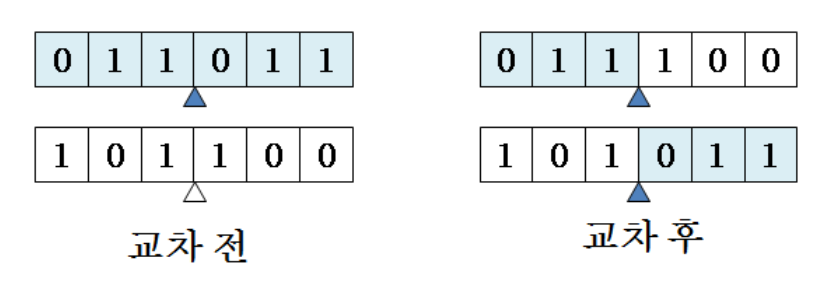
• Probability controls the probability of searching better solutions
  • 101011 is the optimal solution
  • The probability of applying crossover: p
  • The probability of selecting crossover point: 1/5
  • p/5: the probability of finding the optimal solution from the above two parents

3. Mutation 돌연변이

• Introduce a mutation to a candidate solution
• Small change
• Probability of applying mutation in a solution: p
• Issue
  • How large probability with respect to population size, individual length

어떤 위치의 bit 하나를 filp하는 것을 의미한다.

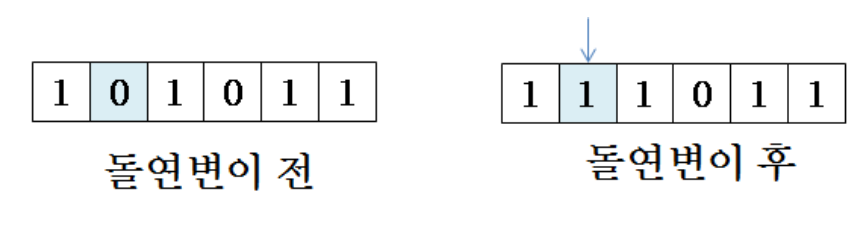
• Break found building blocks
• Used for increasing diversity
• Expect a small probability to observe
  • 돌연변이 확률은 작게 잡지만, 그 작은 확률 덕분에 완전히 새로운 building block이 가끔 등장하길 기대한다.
• If composin building blocks do nt increase fitness monotonically, the mutation is more effective
  $\rightarrow$ very strong dependency between elemetns
• Mutation Rate: (1/PopSize) ~ (1/Length)

염색체 내 요소들 사이 상호 의존성이 강해서 부분 최적 구조의 단순 조합으로는 전역 최적해를 만들기 어려운 경우, 기존 building block을 깨고 완전히 다른 조합을 만드는 돌연변이가 오히려 더 효과적일 수 있다.

돌연변이 연산 역할

돌연변이 연산 후

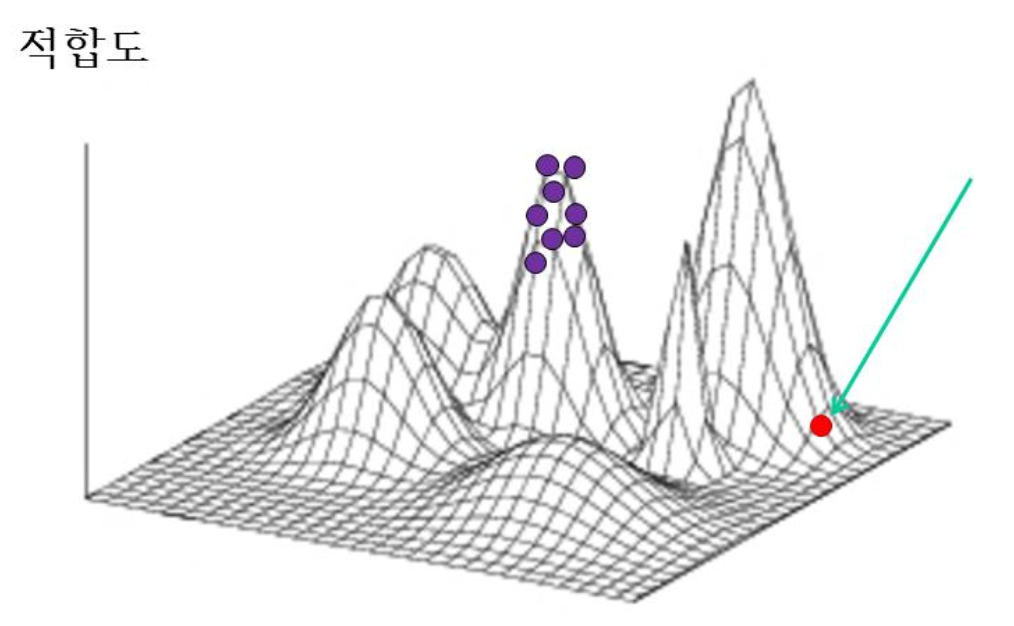
여러 세대가 지난 후

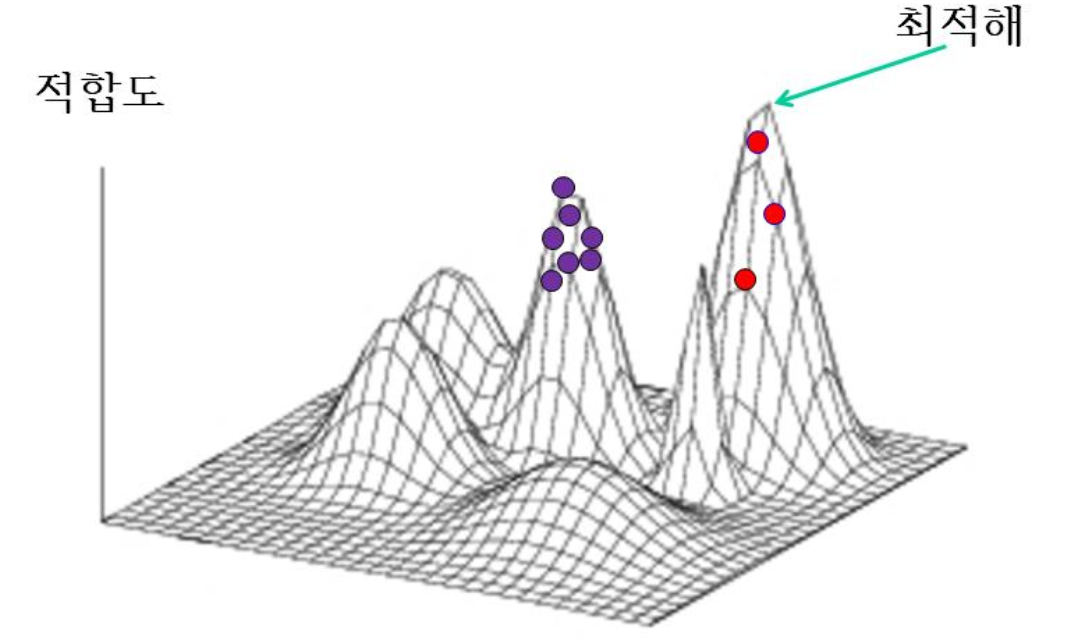
Terminating Condition

• Not constant
  • No guarantee that the genetic algorithm will always find an optimal solution
  • In general, the algorithm is terminated when no more good solutions emerge during the execution of the algorithm $\rightarrow$ threshold

9.4.3 Example of Running GA

• Find an $x$ to maximize $f(x)$ in the range $0 \le x \le 31$
  • $f(x) = -x^2 + 38x + 80$
• Population size: 4
• Selection at the first generation: 1, 29, 3, 10 (assume)
• Fitness of the selected individuals
  • f(1) = 117
  • f(29) = 341
  • f(3) = 185
  • f(10) = 360

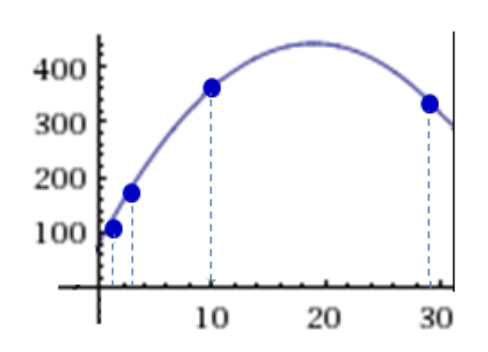
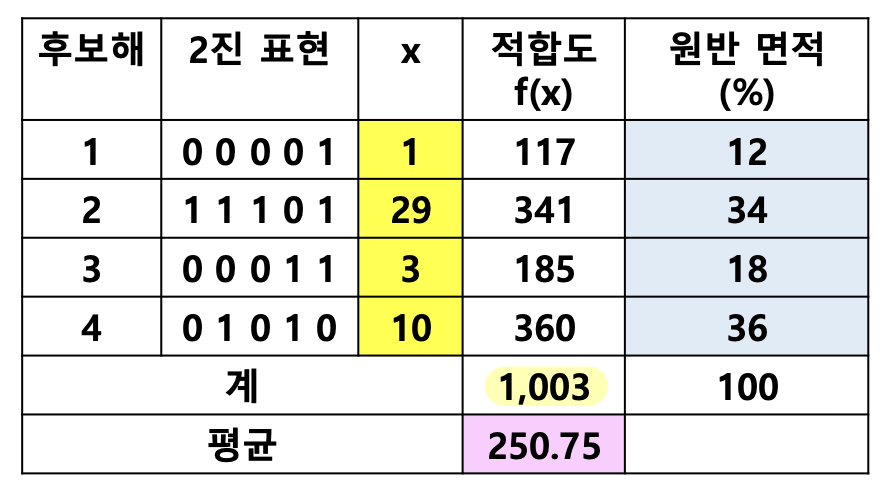
• Roulette-Wheel Selection
• Average fitness in the population: 250.75

Selection

• Non-deterministic, assumption
• 2 x id4, 1 x id2, 1 x id3, 0 x id1

Crossover

• Non-deterministic, assumption
• id2 + id4, id3 + id4
• One point crossover

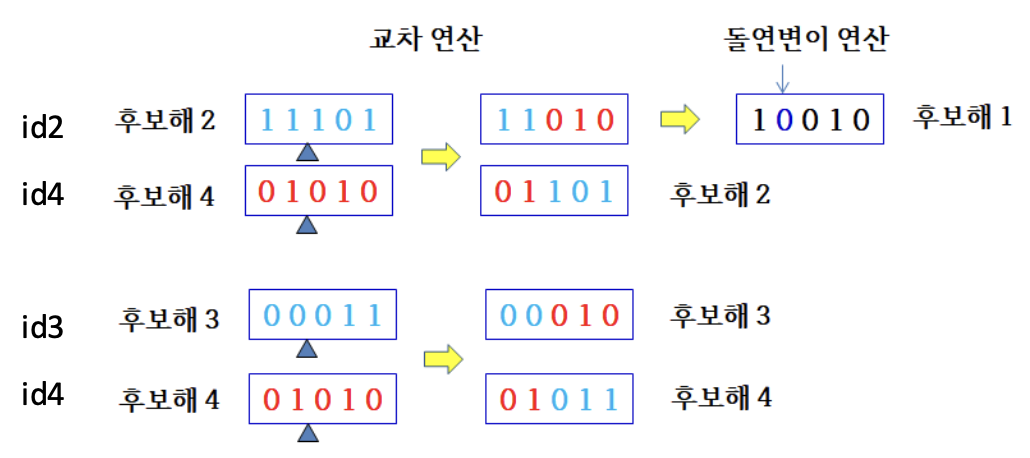
Mutation

• Non-deterministic, assumption
• Generated samples by crossover are mutated

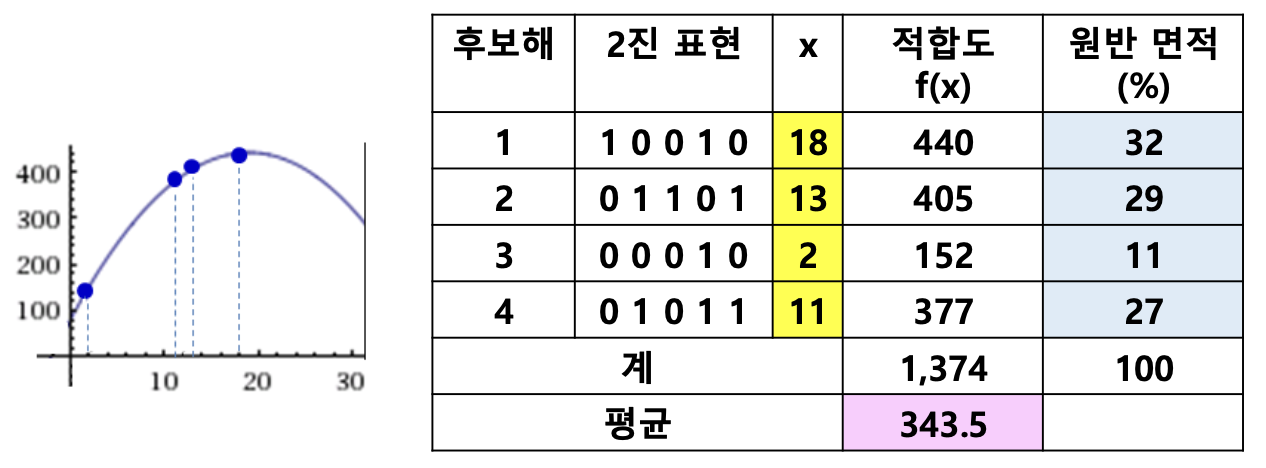
• Average fitness of population at the second generation: 343.5
• Repeat until, the best solution is not improved anymore

9.4.4 Genetic Algorithm for TSP

• Various crossover operators

1. Two-point crossover

• Select two points
• Can represent more expressive building blocks

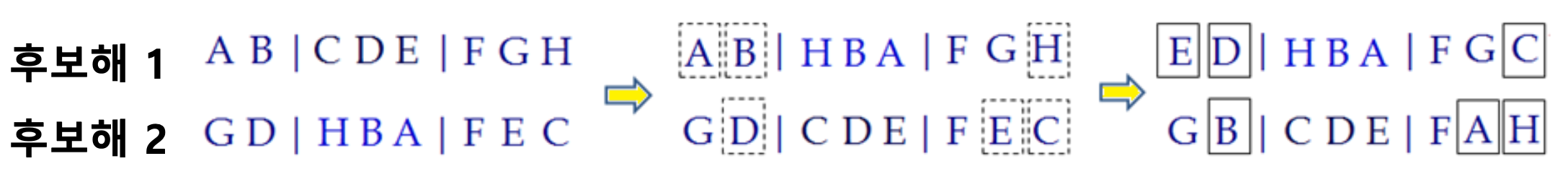
교차 구간은 고정이다.

2. Cycle crossover

• One-point exchange
• Repeat until two solutions make complete solutions

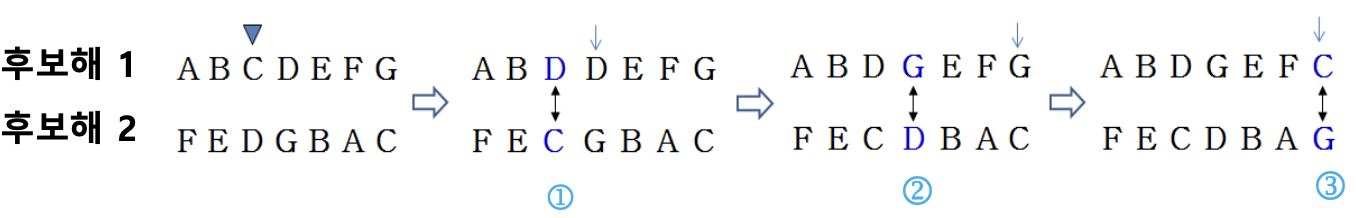
System parameters to empirically tune

1. Population size
2. Selection operator
3. Crossover rate
4. Mutation rate
5. Terminating condition

To improve performance

1. Chromosome representation
2. Operator bias in selecting next subspace for search
3. Exploration and exploitation control
4. Elitism

9.4.5 Advanced Algorithms

• Control of selecting the next search space
  • Probabilistic Model(Estimation of distribution algorithm, CMA-ES)
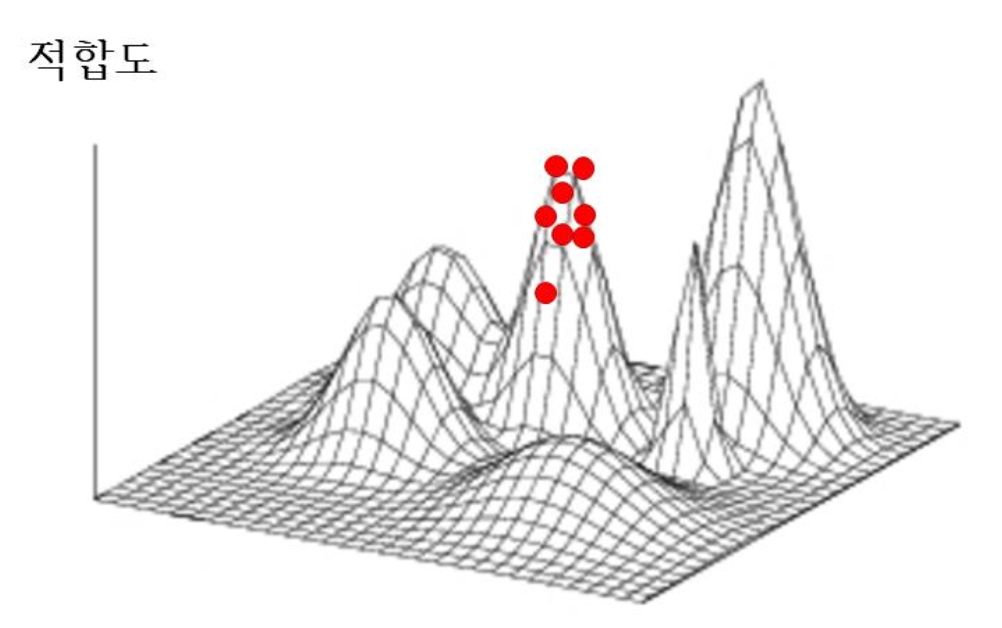
• Multimodal optimization
  • Find k-best solutions independently (particle swarm optimization)
  • Bi-population
• Optimize many objectives (not a single objective form of many objectives) (multi-objective optimization)
• Searching best model (not a single solution for a model)
  • $\rightarrow$ Genetic programming
• Many and many algorithms ...

9.4.6 Applications

• Very good performance for complex problems in general
• Bin-packing
• Task-scheduling
• TSP
• Knapsack problem

Practical Applications

• Robotics
• Signal processing
• Circuit design
• Flight design
• Communication optimization
• Any problem can be solved by GA
  • Area: machine learning, pattern recognition, evolutionary computation