1. Algorithm
알고리즘의 유래
- 9세기경 페르시아 수학자인 알콰리즈미의 이름으로부터 유래
- 최초의 알고리즘: BC 300년 경 유클리드의 GPD 알고리즘
알고리즘이란?
- 문제를 해결하기 위한 단계적인 절차
- 단계적인 절차를 따라 하면 요리가 만들어지듯이, 알고리즘도 단계적인 절차를 따라 하면 주어진 문제의 해를 찾는다.
- 효율적인 알고리즘 고안이 중요
1.1 최대 숫자 찾기
Sequential Search
- 카드의 숫자를 하나씩 비교하면서 본 숫자들 중에서 가장 큰 숫자를 기억해가며 찾기
1.2 임의의 숫자 찾기

Sequential Search
- 최대 숫자 찾기처럼 85를 기억하고 바닥에 펼쳐진 카드를 차례대로 한 장씩 읽으며 85와 비교
- 8장의 카드를 읽은 후에나 85를 찾는다.
오름차순으로 미리 정렬되어 있다면? 이진 탐색
- 중간에 있는 45(혹은 55)와 85를 먼저 비교
- 중간 한 장을 읽어 85와 비교한 것이 첫 카드부터 읽어 나가는 순차 탐색보다 훨씬 빠르게 목표에 다가간다.
Binary Search, K 찾기
- 오름차순으로 데이터 정렬
- 중간 숫자와 K 비교한 후
- 같으면 탐색 성공
- K가 작으면 앞부분 반에서 같은 방법으로 K를 찾고
- K가 크면 뒷부분 반에서 같은 방법으로 K를 찾는다.
1.3 동전 거스름돈
물건을 사고 거스름돈을 동전으로 받아야 한다면? 대부분 경우 가장 적은 수의 동전을 원한다.
거스름돈이 730원이라면?
어떻게 하면 가장 적은 수의 동전을 찾을까?
- 가장 큰 액면의 동전부터 차례로
- 730원에 대해서
- 500원 동전 1개 선택
- 남은 230원에 대해 100원 동전 2개 선택
- 남은 30원에 대해 10원 동전 3개 선택
- 총 동전의 수 = 1 + 2 +3 = 6개
남은 거스름돈 액수를 넘지 않는 한도에서 (욕심 내어) 가장 큰 액면의 동전을 계속해서 선택하는 알고리즘을 Greedy 알고리즘이라고 한다.
1.4 한붓 그리기
종이에서 연필을 떼지 않고 그리는 한붓그리기 문제
- 어느 한 점에서 출발하여 모든 간선을 한 번만 지나서 출발점으로 돌아오되, 궤적을 그리는 동안 연필이 종이에서 떨어져서는 안 된다.
- 단, 점은 여러 차례 방문하여도 무방하다.
- Euler Circuit
어떻게 해결 방법을 찾아야 할까?
- 그래프가 작으면 연필로 시행착오를 통해서
- 그래프가 크면 그래프의 어느 점까지 진행하여 왔을 때, 다음에 어느 점으로 이동해야 할지를 결정하기가 쉽지 않다.
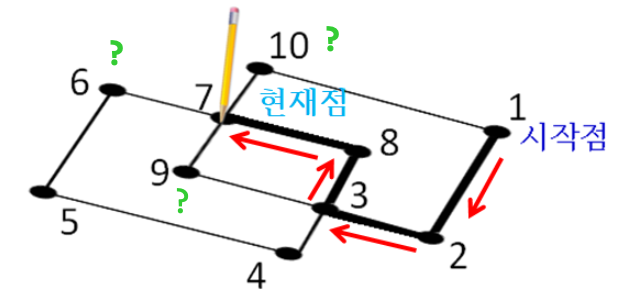
- 현재 점 7로부터 점 6, 9, 10 중에서 어디로 진행해야 할까?
점 6, 9, 10을 살펴보자
- 점 6으로 가면 5, 4, 3, 9, 7, 10을 거쳐서 점 1로 돌아올 수 있다.
- 점 9로 가면 3, 4, 5, 6, 7, 10을 거쳐서 역시 점 1로 돌아올 수 있다.
- 점 10으로 가면 점 1로 갈 수 밖에 없고, 나머지 간선들을 지나기 위해서는 연필을 떼어야 한다.
점 6, 9의 공통점은?
- 현재 점으로부터 점 6이나 점 9를 지나서 현재 점으로 돌아오는 사이클이 있다.
- 즉 현재 점에서 점 6이나 점 9로 이동하면, 연필을 떼지 않고 진행할 수 있다.
- 점 10을 지난 후, 남아있는 간선들을 연결해서는 현재 점으로 돌아올 사이클이 남아있지 않다.
현재 점에서 현재 점으로 돌아오는 사이클이 존재하며, 이는 폐공간 또는 크루스칼 구조와 같다.
현재 점으로 돌아오는 사이클이 있으면 진행하고, 인접한 점이 하나밖에 없으면 사이클 체크 없이 인접한 점으로 진행한다.
1.5 미로 찾기
알고리즘이 없던 옛날, 미로 찾기의 해는 바로 실타래였다.
하지만 실제 미로 문제의 대부분은 실타래가 없다. 이러한 상황에서 어떻게 미로를 빠져나올 수 있을까?
일반적인 방법
- 현 위치에서 한 방향을 선택하여 이동하고,
- 길이 막혀 있으면 다시 되돌아 나오며,
- 다른 방향으로 다시 시도
- 가능하다면 지나갔던 곳을 표시해 놓고(stack) 다시 안 간다.
그러나 일반적인 방법은 어두운 곳에서는 사용이 불가하다. 이렇게 어려운 상황에서도 답은 존재하는데, 무엇일까?
오른손 법칙
- 현 위치에서 한 방향을 선택하고, 오른손을 벽에 댄다.
- 그리고 출구가 나올 때까지 계속 오른손을 벽에서 떼지 않고 계속 걸어간다.
- 이 방법은 실타래나 특별한 표시가 필요 없이도 항상 출구를 찾는다.
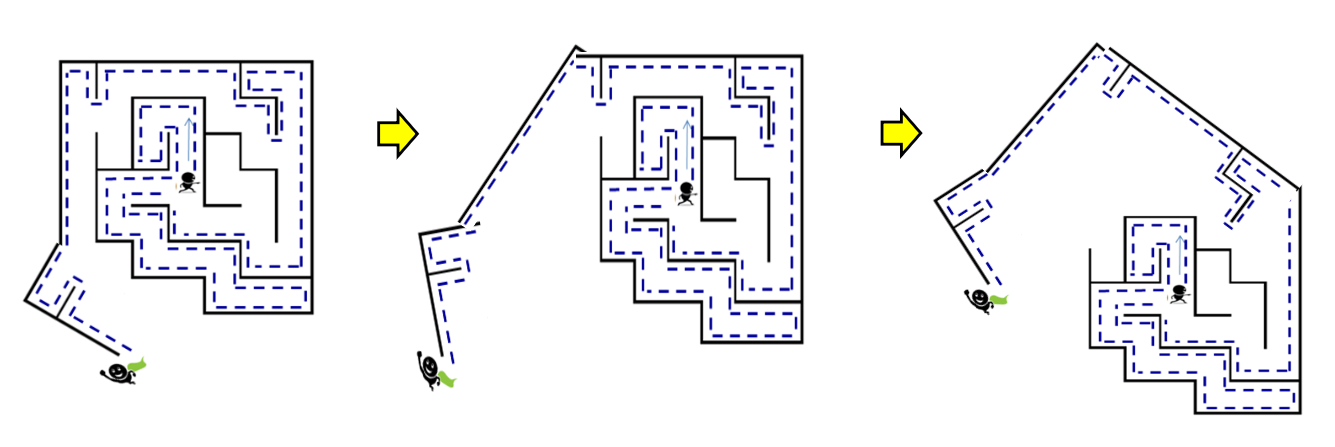
벽이 완전히 닫혀 있거나, 동떨어진 영역이 있다면 오른손 법칙이 항상 성공하지 않는다.
미로가 어떤 종이 박스로 만들어져 있다고 생각해보면, 계속 펼치면 선이 된다.
1.6 가짜 동전 찾기
아주 많은 동전 속에 1개의 가짜 동전이 있다. 가짜 동전의 무게는 정상적인 동전보다 약간 가볍다.
최소의 양팔 저울을 사용하는 횟수로 가짜 동전을 찾아내라.
- 동전 1개를 저울 왼편에 올리고, 나머지 동전을 하나씩 오른편에 올려서 가짜 찾기
- 1 ~ (n-1)회
- 총 동전 수가 n이라면, n-1번 저울을 재야 한다.
- 동전을 2개씩 짝을 지어, n/2짝을 각각 저울에 달아서 가짜 찾기
- 1 ~ n/2회
- 최악의 경우 저울 사용 횟수가 거의 1/2로 감소
- 동전 더미를 반으로 나누어 저울 양편에 올리기
- 남은 동전 수는 계속 1/2로 줄어들고, 나중에 2개가 남았을 때 가짜 동전을 가려낸다.
- 이 알고리즘은 항상 마지막에 가짜 동전을 찾기 때문에, 운이 좋을 때가 없다.
1024개의 동전은 몇 번 저울에 달아야 할까?
- 먼저 512개씩 양쪽에 올려 재고, 다음은 256개씩, 128개씩,..., 마지막에는 1개씩 올려서 저울을 잰다.
- 이는 총 10번이고, 이다.
- Divide-and-Conquer
n개가 있다면 번 저울에 달면 가짜 동전을 찾는다.
최악의 경우 비교
(1)은 1023번, (2)는 512번, (3)은 10번으로 이 차이는 n이 커지면 더욱 더 커진다.
1.7 독이 든 술단지
독이 든 술단지를 반드시 일주일 만에 찾아야 하는데, 이때 독을 조사하는 신하의 수를 가능한한 줄여야 한다.
입력의 크기가 아주 작을 때에 문제의 답을 찾아서 힌트를 얻는다.
2개일 때
- 한 명의 신하가 1개의 술단지의 술을 맛본다.
- 일주일 후
- 신하가 살아 있으면, 맛보지 않은 단지에 독이 있다.
- 죽는다면, 맛본 술에 독이 있다.
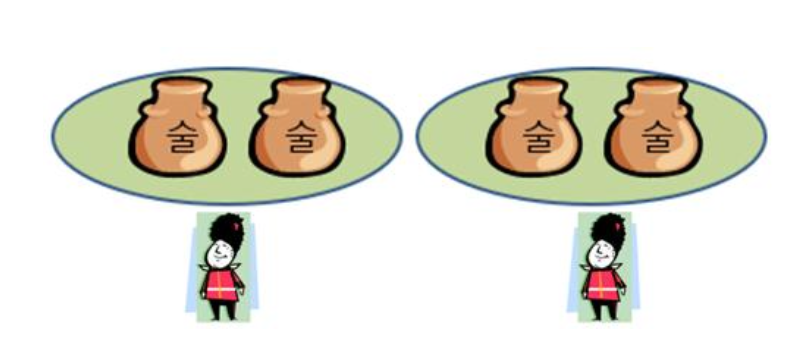
4개일 때
- 세 사람이 각각 한 개씩 맛본다면?
- 두 사람으로 줄일 수는 없을까?

- 두 사람이 각각 한 단지씩 맛보게 해보면
- 나머지 2개의 단지 중 어느 하나에 독이 들어 있는지 알 수 없다.

- 4개의 단지를 두 그룹으로 나누어, 각 그룹에 한 사람씩 할당해보자
- 정답이 어느 단지인지를 알려면 또 일주일이 필요하므로 실패
Solution
- 한 명의 신하가 반드시 하나의 단지의 술만 맛보아야 하는 것으로 생각했다.
- 문제에는 이러한 조건이 없기 때문에 이것이 문제 해결의 실마리이다.
Idea
- 4개의 단지 중에서, 시음하지 않은 두 개의 단지 중에 하나를 두 신하에게 동시에 맛 보게 하자.
- 이렇게 하면 4가지의 결과가 생긴다.

- 아무도 시음하지 않은 단지에 독 -> 일주일 후에 두 신하 둘 다 살아있다.
- A가 혼자 시음한 단지에 독 -> 일주일 후에 A만 죽는다.
- B가 혼자 시음한 단지에 독 -> 일주일 후에 B만 죽는다.
- A와 B 둘 다 시음한 단지에 독 -> 일주일 후에 둘 다 죽는다.
Algorithm
2진수를 활용해 해를 찾는다.
- 각 단지에 2진수를 0부터 부여하고, 첫 비트가 1이면 신하 1이 맛본다. 둘째 비트가 1이면 신하 2가 맛본다. k번째 비트가 1이면 신하 k가 맛본다.
- 술단지가 수가 n이면, 희생자 수가 ~ 이다.
