2. What is Algorithm?

2.1 알고리즘이란?

• 컴퓨터 문제를 해결하는 단계적 절차, 방법
• 알고리즘에는 입력이 주어지고, 알고리즘은 수행한 결과인 해를 출력한다.

알고리즘의 일반적 특성

• 정확성
  • 주어진 입력에 대해 올바른 해 제공
• 수행성
  • 각 단계는 컴퓨터에서 수행 가능해야 함
• 유한성
  • 유한 시간 내에 종료되어야 함
• 효율성
  • 효율적일수록 그 가치는 높아짐

2.2 최초의 알고리즘

• Euclid의 최대공약수 알고리즘
  • 기원전 300년 경에 만들어진 가장 오래된 알고리즘
  • 최대공약수란 2개의 자연수의 공약수들 중에서 가장 큰 수

2개의 자연수의 최대공약수는 큰 수에서 작은 수를 뺀 수와 작은 수의 최대공약수와 같다.

유클리드의 최대공약수 알고리즘에서 뺄셈 대신에 나눗셈을 사용하면 빠르게 해를 찾는다.

Algorithm

Euclid(a, b)
Input: 정수 a, b; 단,$a \geq b \geq 0$
Output: 최대공약수(a,b)

if b==0 return a 
return Euclid(b, a mod b) 

2.3 알고리즘의 표현 방법

알고리즘의 각 단계는 보통 말로 서술할 수 있으며, 컴퓨터 프로그래밍 언어로만 표현할 필요는 없다.
일반적으로 알고리즘은 프로그래밍 언어와 유사한 pseudo code로 표현한다.

최대 숫자 찾기

카드의 숫자를 하나씩 비교하면서 본 숫자들 중에서 가장 큰 숫자를 기억해가며 찾는다. 마지막 카드의 숫자를 본 후에, 머릿속에 기억된 가장 큰 숫자가 적힌 카드를 바닥에서 집어든다.

• 자연어로 표현

• pseudo code

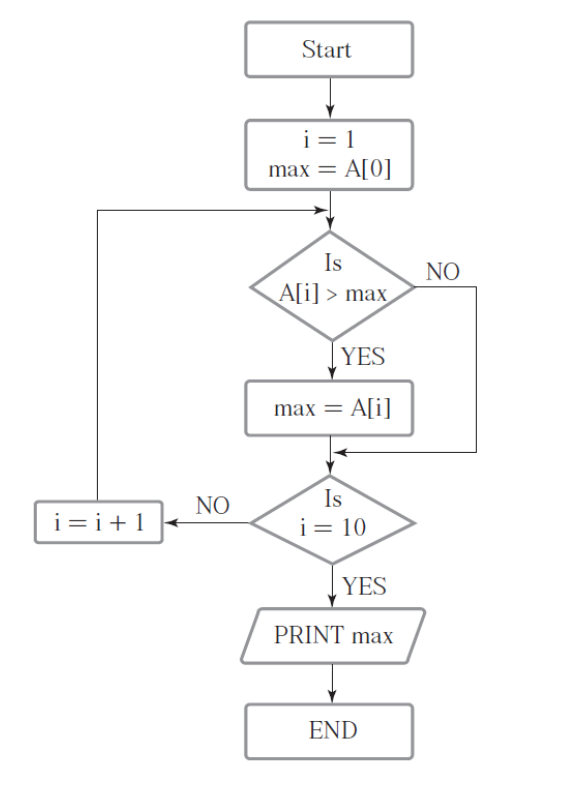
  max = A[0]
  for i = 1 to 9
  if (A[i] > max) max = A[i]
  return max 

• flow chart

  

2.4 알고리즘의 분류

문제의 해결 방식에 따른 분류

• Divide-and-Conquer 분할 정복
• Greedy 그리디
• Dynamic Programming 동적 계획
• Approximation 근사
• Backtracking 백트래킹
• Branch-and-Bound 분기 한정

문제에 기반한 분류

• 정렬
• 탐색
• 그래프
• 기하

특정 환경에 따른 분류

• Parallel 병렬
• Distributed 분산
• Quantum 양자

패러다임에 의한 분류

• 기존 규칙 기반 알고리즘 - 알고리즘 수업에서 다루는 것들
• 학습 기반 알고리즘
  • Shallow ML, Deep ML, Transformer, Bayesian methods
  • Evolutionary/Genetic Algorithms

2.5 알고리즘의 효율성 표현

• 알고리즘의 수행 시간 또는 알고리즘이 수행하는 동안 사용되는 메모리 크기
• 시간 복잡도, 공간 복잡도
  • 일반적으로 알고리즘들을 비교할 때에는 시간 복잡도가 주로 사용됨

시간 복잡도

• 알고리즘이 실행되는 동안에 사용된 기본적인 연산 횟수를 입력 크기의 함수로 나타냄
  • 기본 연산: 데이터 간 크기 비교, 데이터 읽기, 갱신, 숫자 계산 등과 같은 단순한 연산
• e.g. 10장의 숫자 카드들 중에서 최대 숫자 찾기
  • 순차 탐색으로 찾는 경우에 숫자 비교가 기본적인 연산, 총 비교 횟수는 9번
  • n장의 카드가 있다면, n-1번의 비교 수행으로 시간 복잡도는 $f(n) = T(n) = n-1$

알고리즘의 복잡도 표현 방법

• Worst-case Analysis
  • '어떤 입력이 주어지더라도 알고리즘의 수행시간이 얼마 이상은 넘지 않는다'라는 Upper Bound
• Average-case Analysis
  • 입력의 확률 분포를 가정하여 분석, 일반적으로 Uniform Distribution 가정
• Best-case Analysis
  • 가장 빠른 수행 시간 분석, Optimal 알고리즘을 찾는데 활용 -> Lower Bound
• Amortized Analysis
  • 일련의 연산을 수행해 총 수행 시간을 합하고 이를 연산 횟수로 나누어 수행 시간 분석
  • 조건: 알고리즘에서 적어도 두 종류의 연산 수행되고, 그 중 하나는 시간이 길고 다른 하나는 짧으며, 수행 시간이 짧은 연산은 많이 수행되고 긴 연산은 적게 수행되어야 의미를 갖는다.
  • amortize는 '분할 상환하다'라는 뜻

일반적으로 알고리즘의 수행 시간은 최악 경우 분석으로 표현

2.6 복잡도의 점근적 표기

• 시간 복잡도는 입력 크기에 대한 함수로 표기

  • 함수: 여러 개의 항을 가지는 다항식
  • 이를 입력 크기에 대한 함수로 표현하기 위해 점근적 표기(Asympotic Notation)를 사용

• 점근적 표기

  • 입력 크기 n이 무한대로 커질 때의 복잡도를 간단하게 표현하기 위해 사용
  • $O$(Big-Oh)
  • $\Omega$(Big-Omega)
  • $\theta$(Theta)

$O$(Big-Oh) - 표기

• 모든 $n \geq n_0$에 대해서 $f(n) \leq cg(n)$이 성립하는 양의 상수 $c$와 $n_0$가 존재하면, $f(n) = O(g(n))$이다.
• $f(n) = O(g(n))$
  • n이 증가함에 따라 $O(g(n))$이 점근적 상한

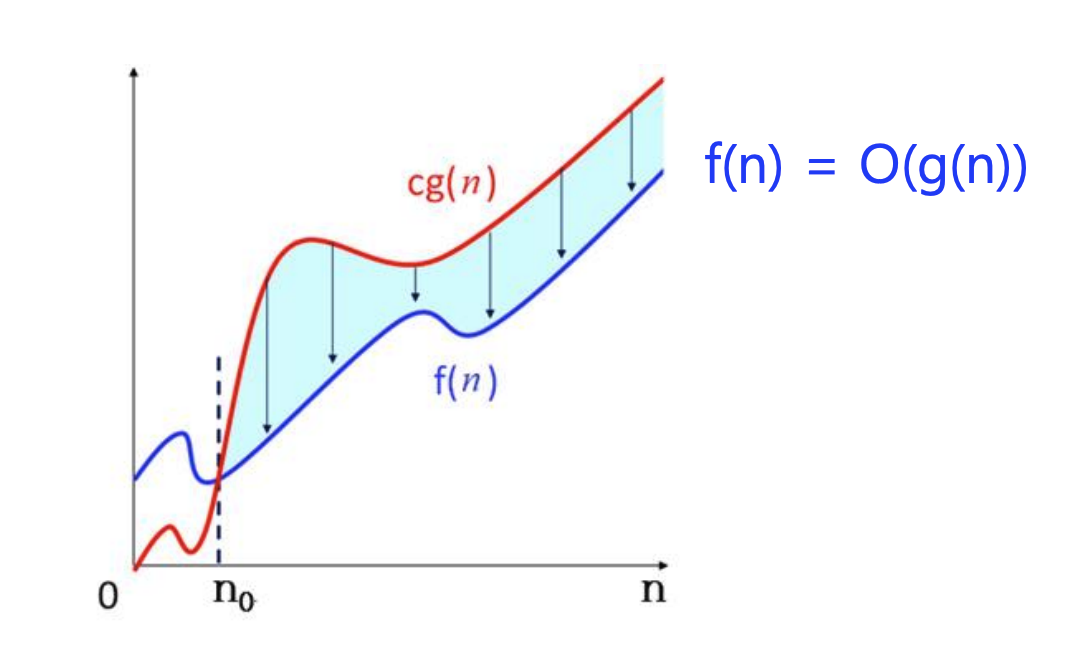
• 다항식에서 최고 차수 항만을 취한 뒤, 그 항의 계수를 제거하여 $g(n)$을 정한다.

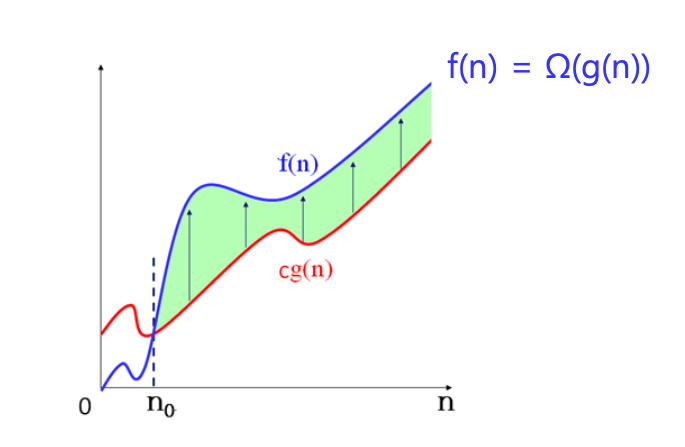
$\Omega$(Big-Omega) - 표기

• 모든 $n \geq n_0$에 대해서 $f(n) \geq cg(n)$이 성립하는 양의 상수 $c$와 $n_0$가 존재하면, $f(n) = \Omega(g(n))$이다.
• $f(n) = \Omega(g(n))$
  • n이 증가함에 따라 $\Omega(g(n))$이 점근적 하한

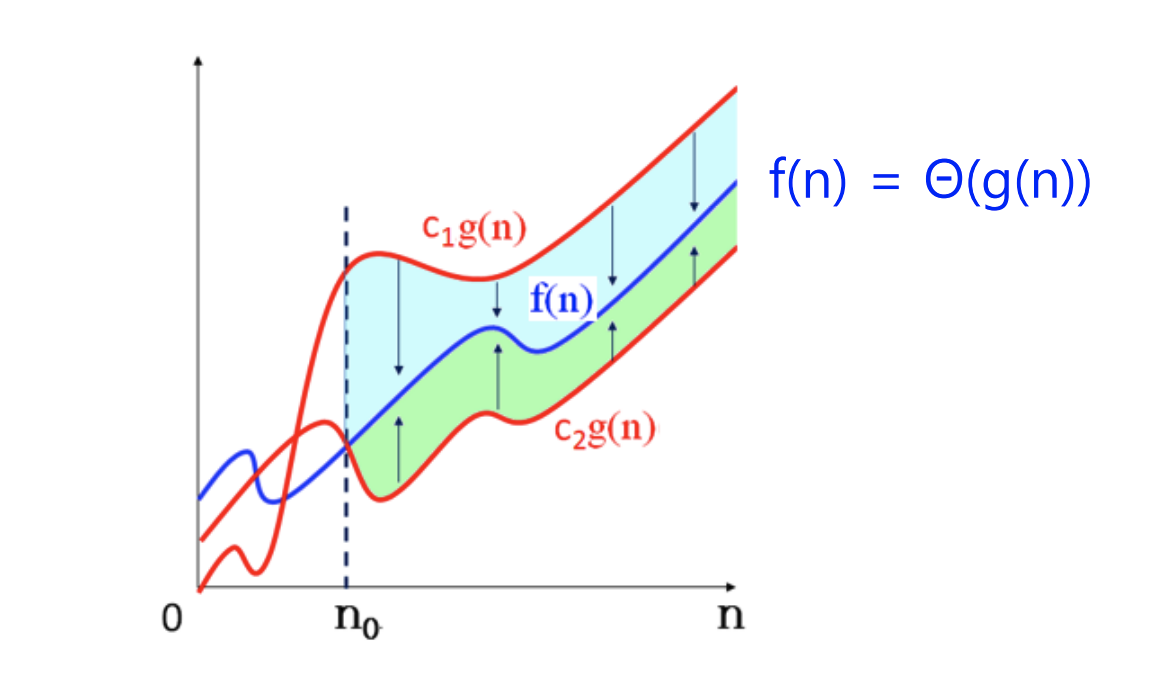
$\theta$(Theta) - 표기

• 모든 $n \geq n_0$에 대해서 $c_1g(n) \geq f(n) \geq c_2g(n)$이 성립하는 양의 상수 $c_1, c_2$, $n_0$가 존재하면, $f(n) = \theta(g(n))$이다.
• $f(n) = \theta(g(n))$
  • 수행시간의 Big-O와 Big-Omega의 표기가 동일한 경우 사용한다. -> 동일한 증가율
  • $n_0$보다 큰 모든 $n$에 대해서 $\theta$ 표기가 상한과 하한을 동시에 만족한다는 것을 보여준다.

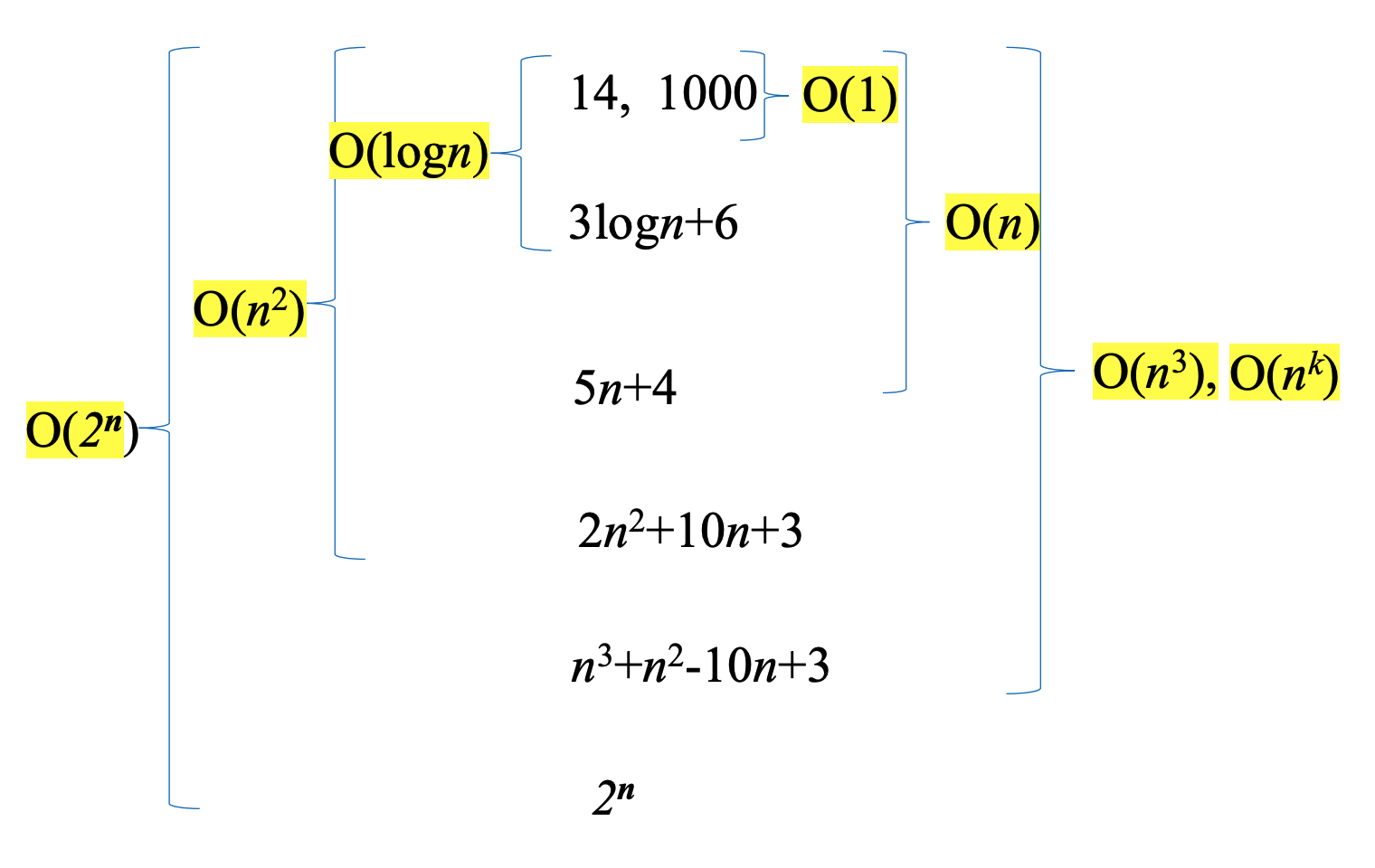
자주 사용하는 $O$-표기

지수 밑으로만 가도 비실용적이라고 말한다.

함수의 증가율 비교

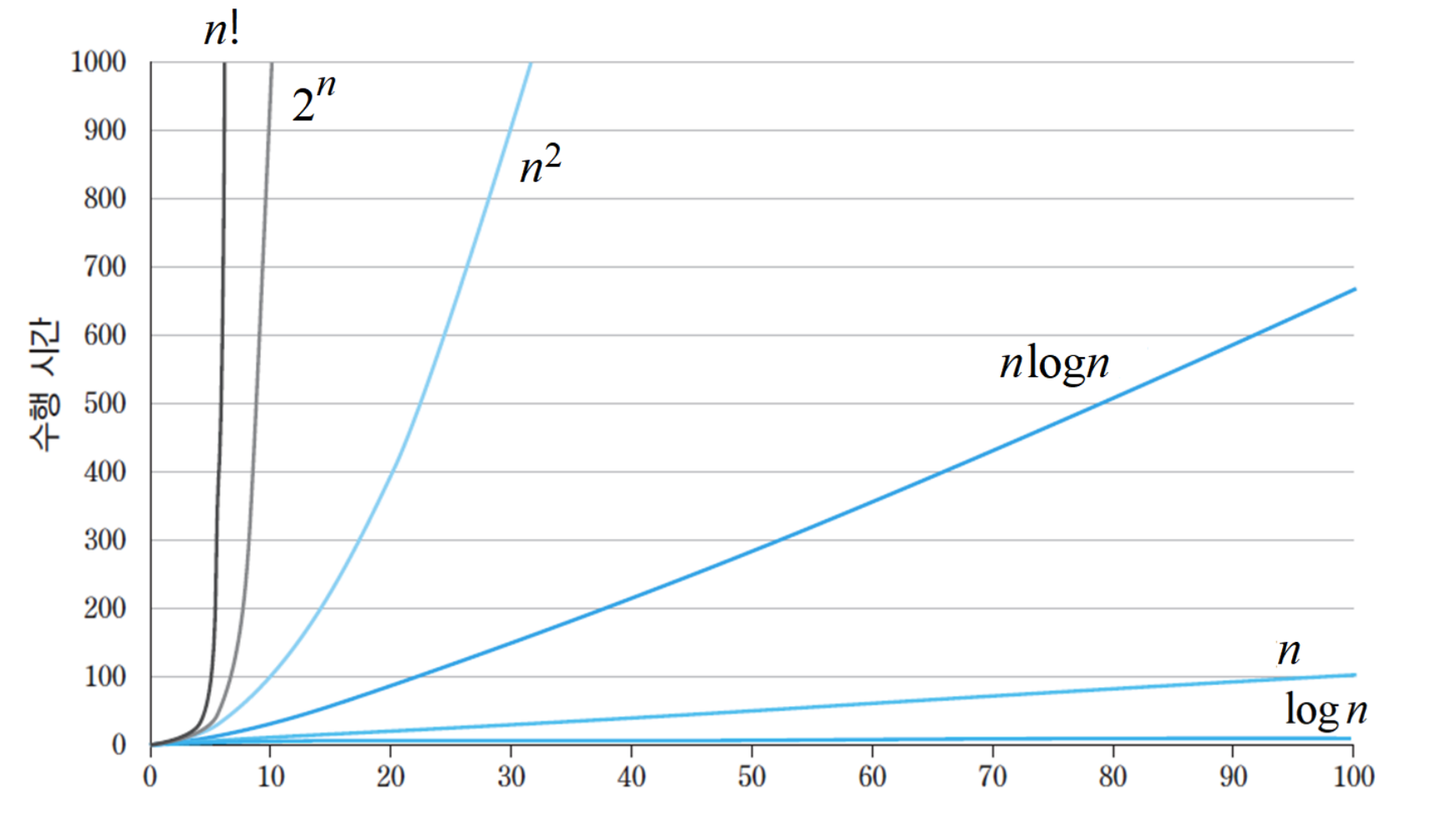
값비싼 hardware 기술 개발보다 효율적인 알고리즘 개발이 훨씬 더 경제적이기 때문에 효율적인 알고리즘은 꼭 필요하다.