6. Sort Algorithm(2)

6.5 Heap sort

6.5.1 Binary heap

• 힙 조건을 만족하는 Complete binary tree
  • 힙 조건: 각 노드의 우선 순위가 자식 노드의 우선 순위보다 높다.
• Maximum heap: 가장 큰 값이 루트에 저장
• Minimum heap: 가장 작은 값이 루트에 저장

완전 이진 트리는 마지막 레벨을 제외한 모든 레벨이 꽉 차있고, 마지막 레벨은 왼쪽부터 차례대로 노드가 채워진 이진 트리이다.

n개의 노드를 가진 힙

• 완전 이진 트리이므로, 힙의 높이가 $log_2n$이며, 노드들을 빈 공간 없이 배열에 저장
• Leaf node를 제외하고, 모두 자식 노드를 2개씩 가짐

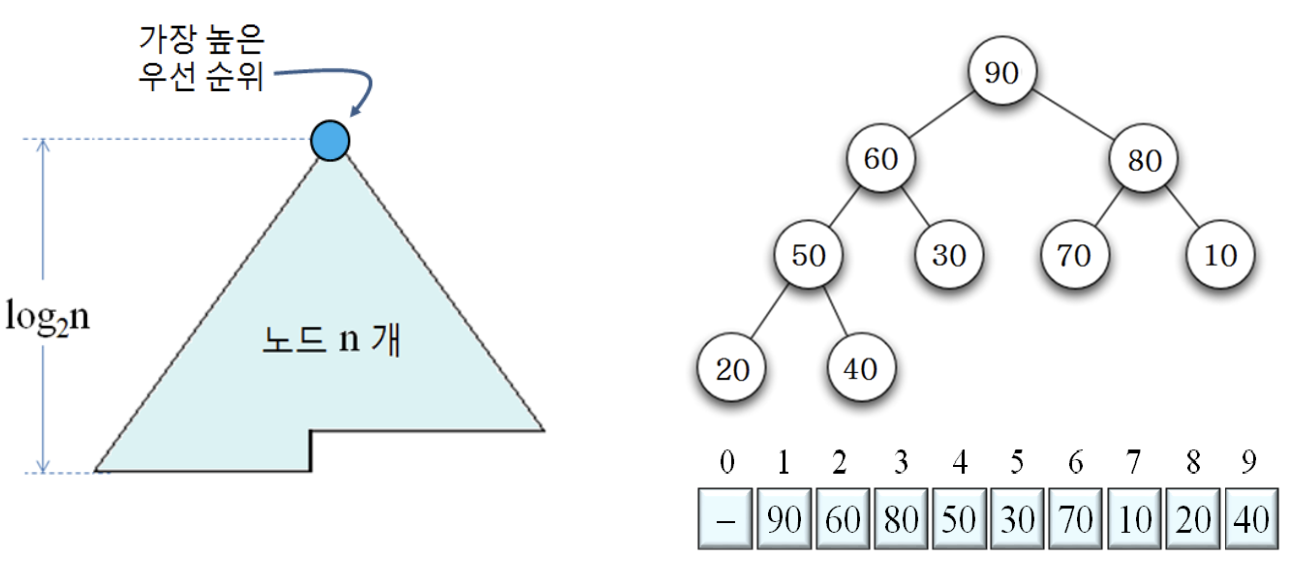
힙의 노드 관계

• 힙에서 부모와 자식의 관계
  • A[i]의 부모 = A[i/2]
    • 단, i가 홀수이면, i/2에서 정수 부분만
  • A[i]의 왼쪽 자식 = A[2i]
  • A[i]의 오른쪽 자식 = A[2i+1]

6.5.2 Heap sort

• 정렬할 입력으로 최대 힙을 만든다. (최소 힙이면 반대로)
• 힙 루트에 가장 큰 수가 있으므로, 루트와 힙의 가장 마지막 노드를 교환한다.
  • 가장 큰 수를 배열의 맨 뒤로 옮기는 것
• 힙 크기를 1개 줄인다.
• 루트에 새로 저장된 숫자로 인해 위배된 힙 조건을 해결 $\rightarrow$ 힙 조건 만족
• 이 과정을 반복하여 정렬

6.5.3 HeapSort()

• Input: 입력이 A[1]부터 A[n]까지 저장된 배열 A
• Output: 정렬된 배열 A

1. A의 숫자에 대해 최대 힙을 만든다.
2. heapSize = n // 힙 크기 조절 변수
3. for i = 1 to n-1
4. $\,\,\,\,$ A[1] $\leftrightarrow$ A[heapSize] // 루트와 힙의 마지막 노드 교환
5. $\,\,\,\,$ heapSize = heapSize - 1 // 힙 크기 1 감소
6. $\,\,\,\,$ DownHeap() // 위배된 힙 조건 만족
7. return A

6.5.4 DownHeap()

• 루트로부터 자식들 중에서 큰 값을 가진 자식과 비교하여 힙 속성이 만족될 때까지 숫자를 교환하며 리프 방향으로 진행

6.5.5 Procedure

HeapSort 알고리즘에서 사용하는 트리 구조는 초기에 반드시 Max-Heap 구조이므로, 항상 루트 노드가 해당 구간에서 가장 큰 값을 지니게 된다.

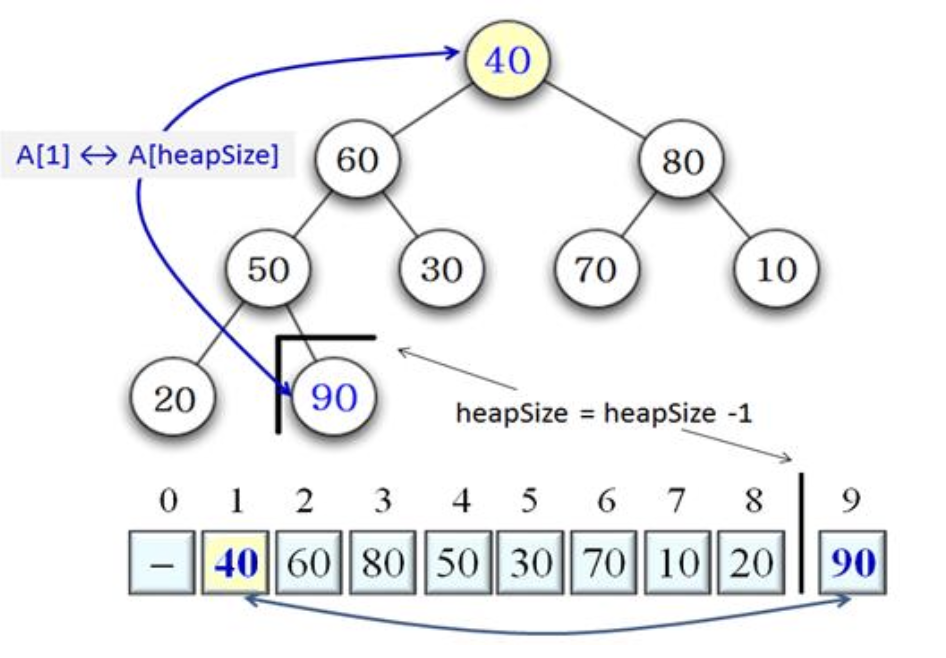
1. 루트와 힙의 마지막 노드 교환

• 힙의 마지막 노드 40과 루트 90을 교환하고, heapSize 1 감소

DownHeap()

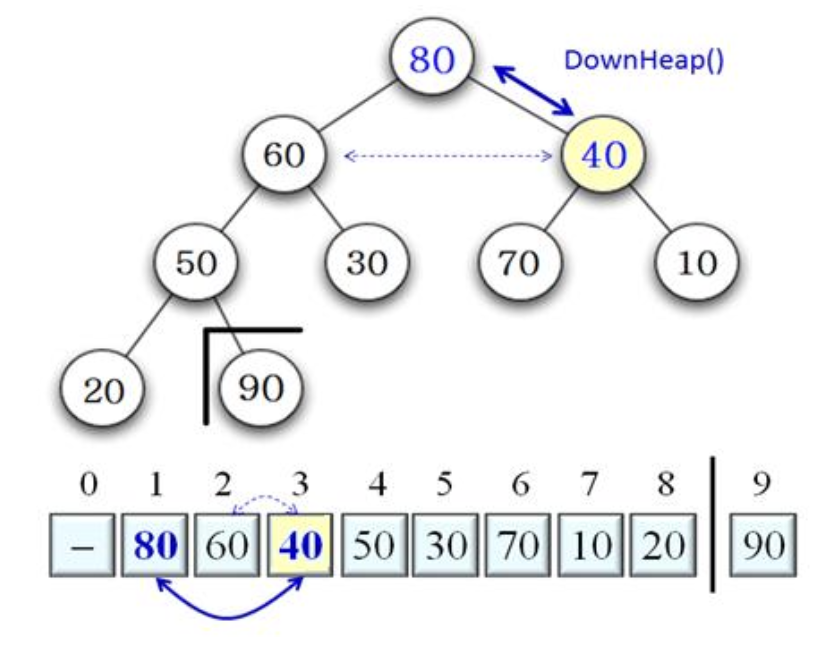
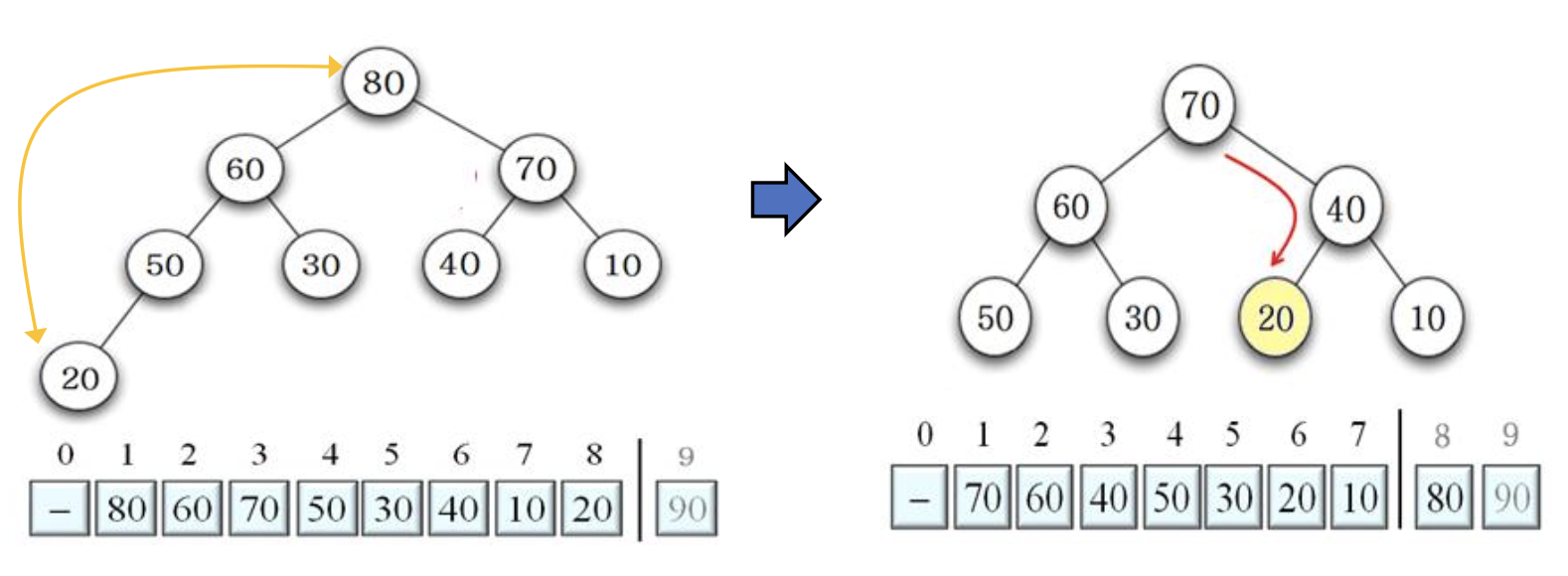
• 루트에 저장된 40이 자식 노드인 60과 80보다 작으므로, 자식 중 큰 80과 루트 40 교환

DownHeap()

• 40은 다시 자식 노드 70과 10 중에서 큰 자식 70과 비교하여, 70과 40 교환

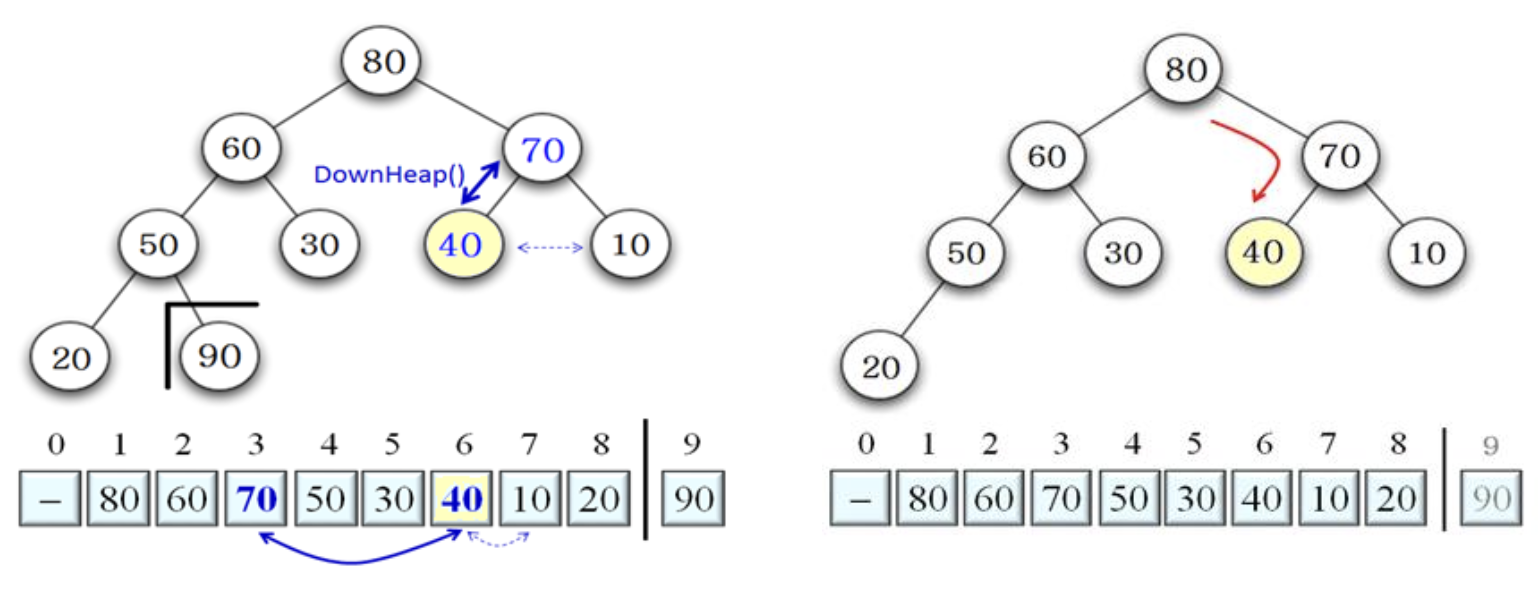
루트와 바꾼 마지막 노드를 리프에 닿을 때까지 아래로 내리면서 힙 조건이 맞을 때까지 반복한다.

80 $\leftrightarrow$ 20 교환 후, DownHeap 수행 결과

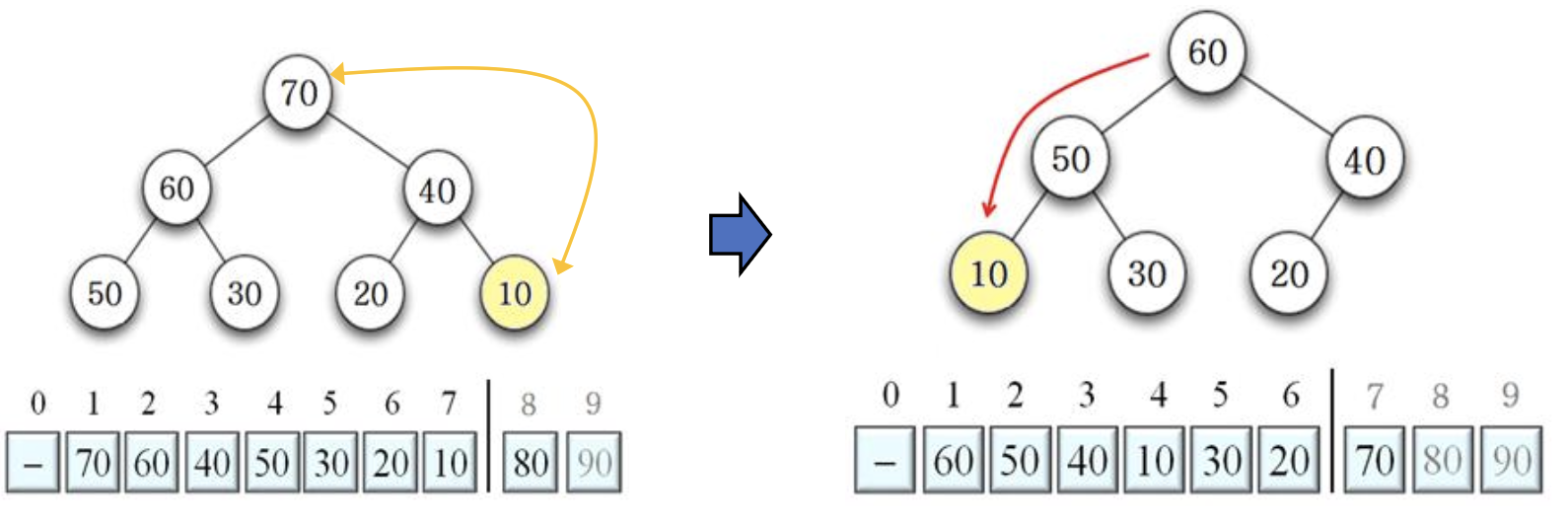
70 $\leftrightarrow$ 10 교환 후, DownHeap 수행 결과

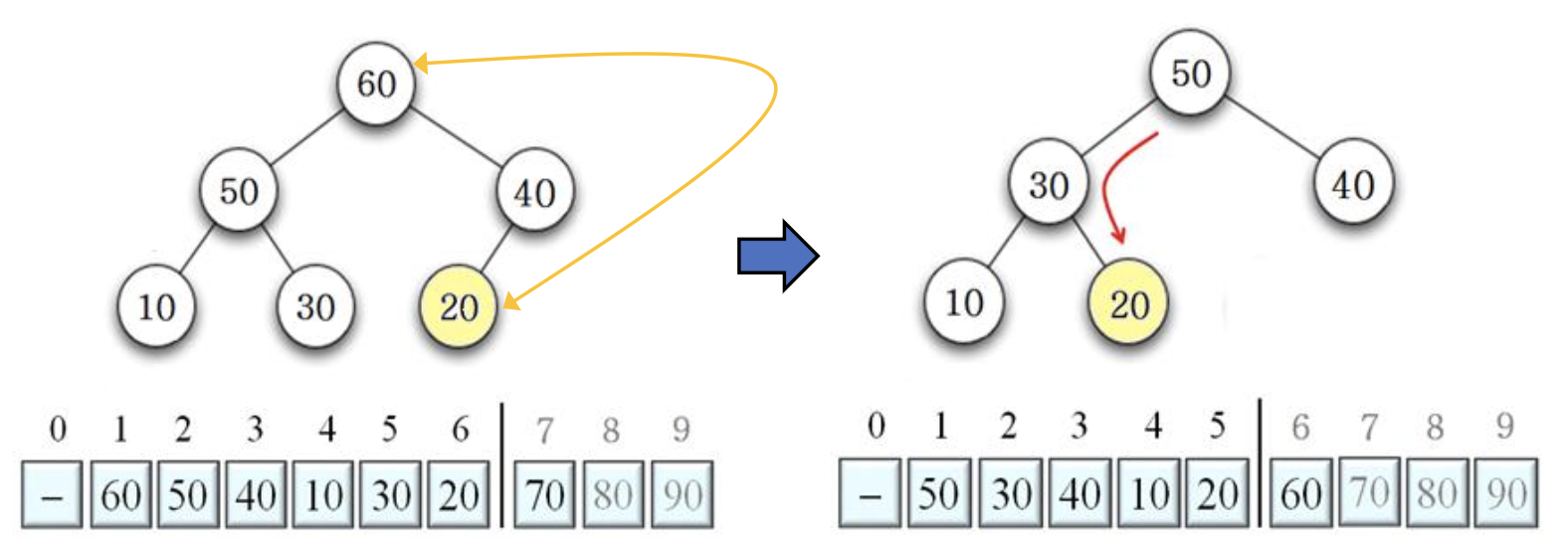
60 $\leftrightarrow$ 20 교환 후, DownHeap 수행 결과

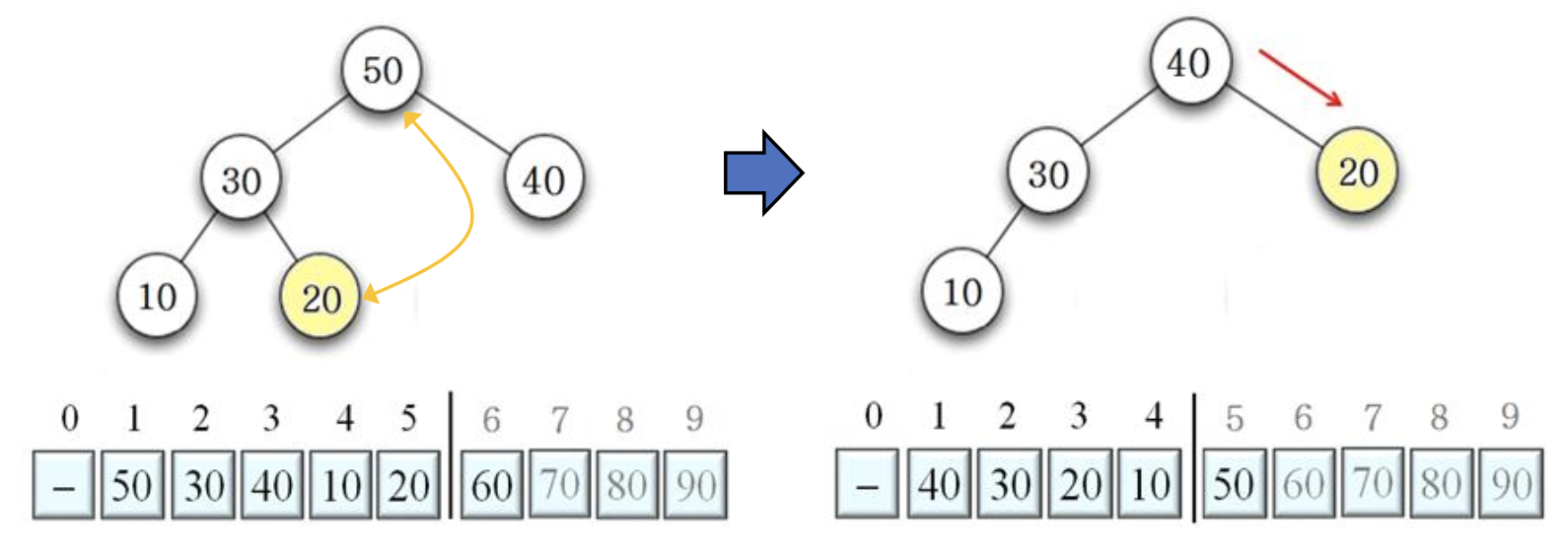
50 $\leftrightarrow$ 20 교환 후, DownHeap 수행 결과

40 $\leftrightarrow$ 10 교환 후, DownHeap 수행 결과

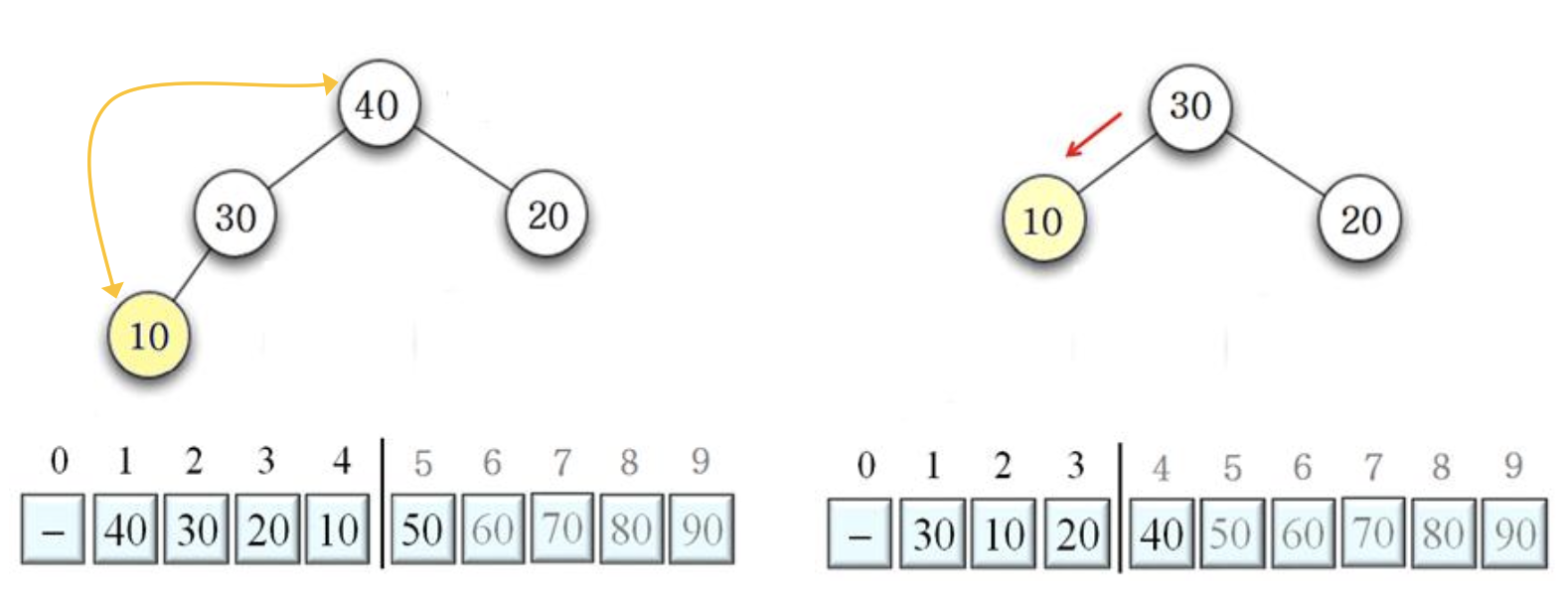
30 $\leftrightarrow$ 20 교환 후, DownHeap 수행 결과

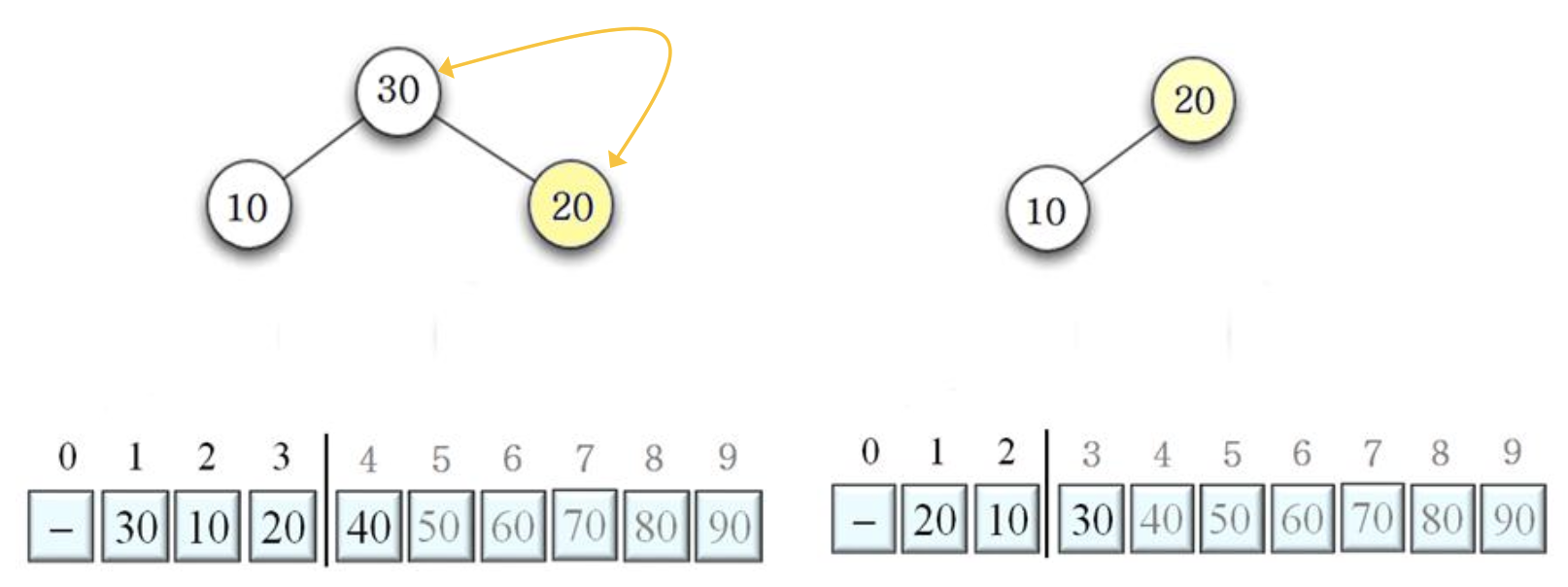
20 $\leftrightarrow$ 10 교환 후, DownHeap 수행 결과

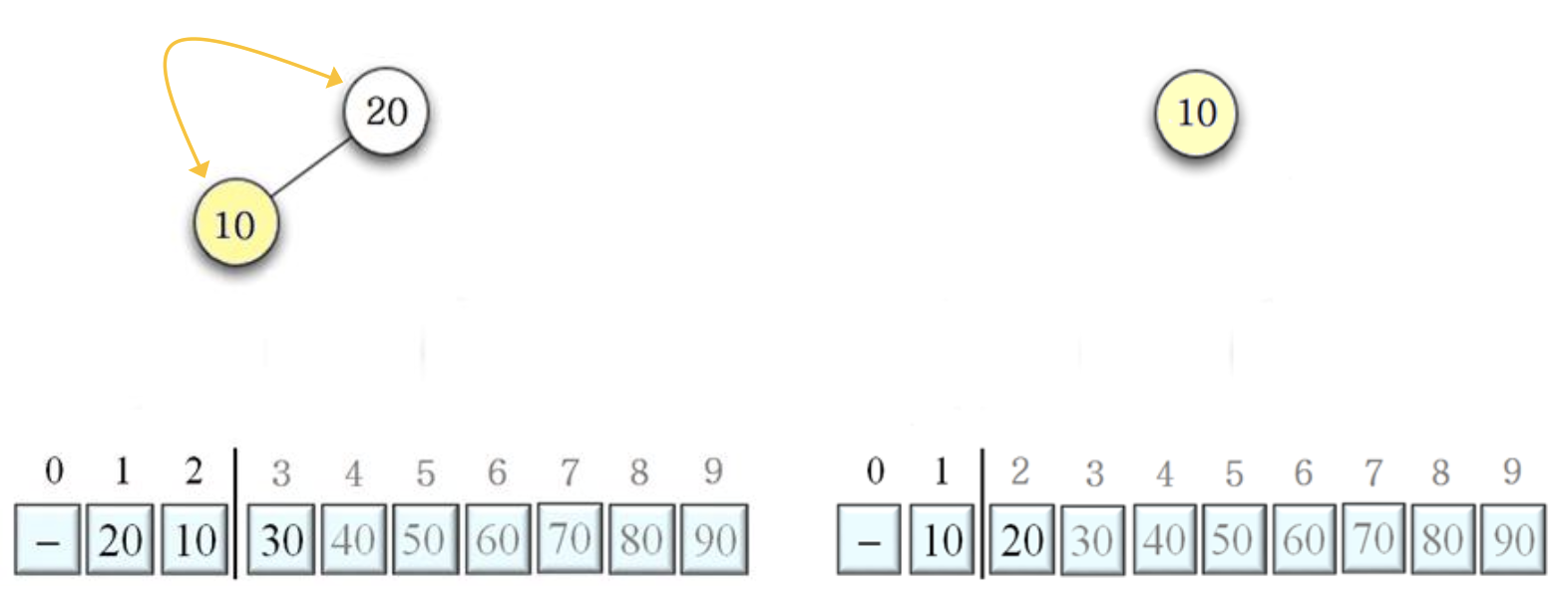
6.5.6 Time complexity

• 힙 만드는 데 $O(n)$
• for-loop는 (n-1)번 수행
  • loop 내부는 $O(1)$
• DownHeap은 $O(logn)$ 시간

$O(n) + (n-1) \times O(logn) = O(nlogn)$

초기 Heap 생성과 DownHeap sort는 순차적으로 수행되기 때문에, 더해서 전체 복잡도로 표기한다.

6.5.7 Characteristic

• 큰 입력에 대해 Downhap()을 수행할 때, 자식을 찾아야 하므로 너무 많은 캐시 미스로 Page fault 발생
• 최선, 최악, 평균 시간 복잡도가 동일

Internal sort time complexity

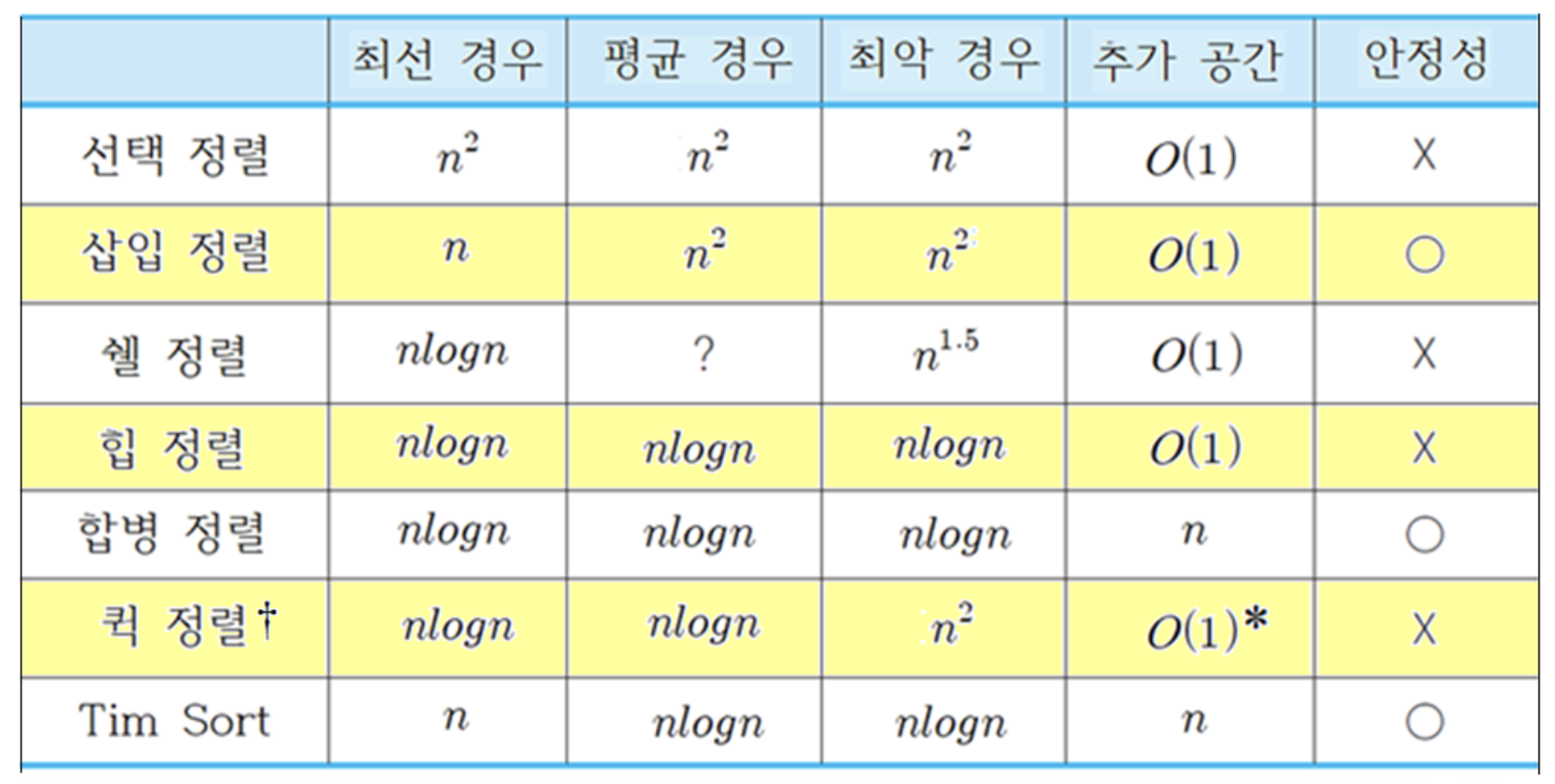
• 퀵 정렬에서 수행되는 순환 호출까지 고려한 추가 공간은 $O(logn)$
• 이중 피벗 퀵 정렬의 이론적인 성능은 퀵 정렬과 같다.

속도: Bubble > Selection > Insertion > Shell > Heap > Merge > Quick

---

6.6 Sort's lower bound

비교 정렬 (Comparison sort)

• 버블 정렬, 선택 정렬, 삽입 정렬, 쉘 정렬, 힙 정렬, 합병 정렬, 퀵 정렬의 공통점은 비교가 부분적이 아닌 숫자 대 숫자로 이루어진다.
• 숫자 전체를 온전히 비교

기수 정렬(Radix sort)은 비교 정렬이 아님

• 숫자들을 한 자리씩 부분적으로 비교

어떤 주어진 문제에 대해 시간 복잡도의 하한이라 함은 어떠한 알고리즘도 문제의 하한보다 빠르게 구할 수 없음을 의미한다.

• 문제의 하한은 어떤 특정 알고리즘에 대한 시간 복잡도의 하한을 뜻하는 것이 아님
• 문제가 지닌 고유한 특성 때문에 어떠한 알고리즘일지라도 해를 찾으려면 적어도 하한의 시간 복잡도만큼 시간이 걸린다.

6.6.1 Lower bound of find maximum

• 최댓값을 찾기 위해 숫자들을 적어도 몇 번 비교해야 하는가?
• 어떤 방식으로 탐색하든지 적어도 (n-1)번의 비교가 필요하다.
  • 왜냐하면 어떤 방식이라도 각 숫자를 적어도 한번 비교해야
  • (n-1)보다 작은 비교 횟수가 의미하는 것은 n개의 숫자 중에서 적어도 1개의 숫자는 비교되지 않았다는 것
  • 비교 안 된 숫자가 가장 큰 수일 수도 있기 때문에, (n-1)보다 적은 비교 횟수로는 최댓값을 항상 찾을 수는 없다.

6.6.2 Lower bound of sort

• 3개의 서로 다른 숫자 $x, y, z$에 대해서, 정렬에 필요한 모든 경우의 숫자 대 숫자 비교
  • 각 내부 노드에서는 2개의 숫자가 비교
  • 비교 결과가 참이면 왼쪽으로, 거짓이면 오른쪽으로 분기
  • 각 리프에 정렬된 결과 저장

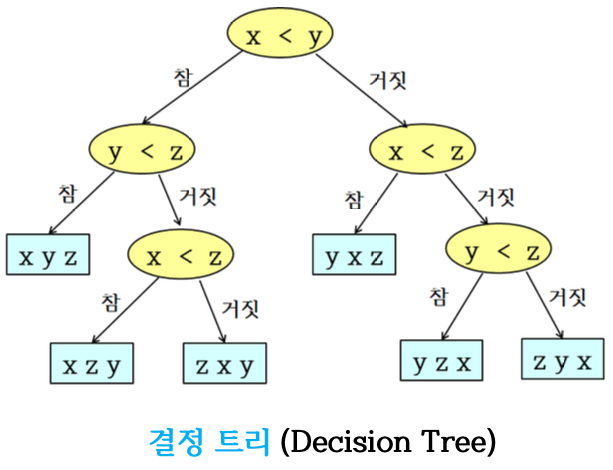
Decision tree

• Leaf의 수 3! = 6
• Decision tree는 binary tree
• 정렬을 하는데 불필요한 내부 노드가 없음
  • 중복 비교를 하는 노드들이 있으나, 이들은 루트로부터 각 리프 노드의 정렬된 결과를 얻기 위해서 반드시 필요한 노드들이다.

어느 경우에도 서로 다른 3개의 숫자가 정렬되기 위해서는 적어도 3번의 비교(결정 트리의 높이:h)가 필요하다.

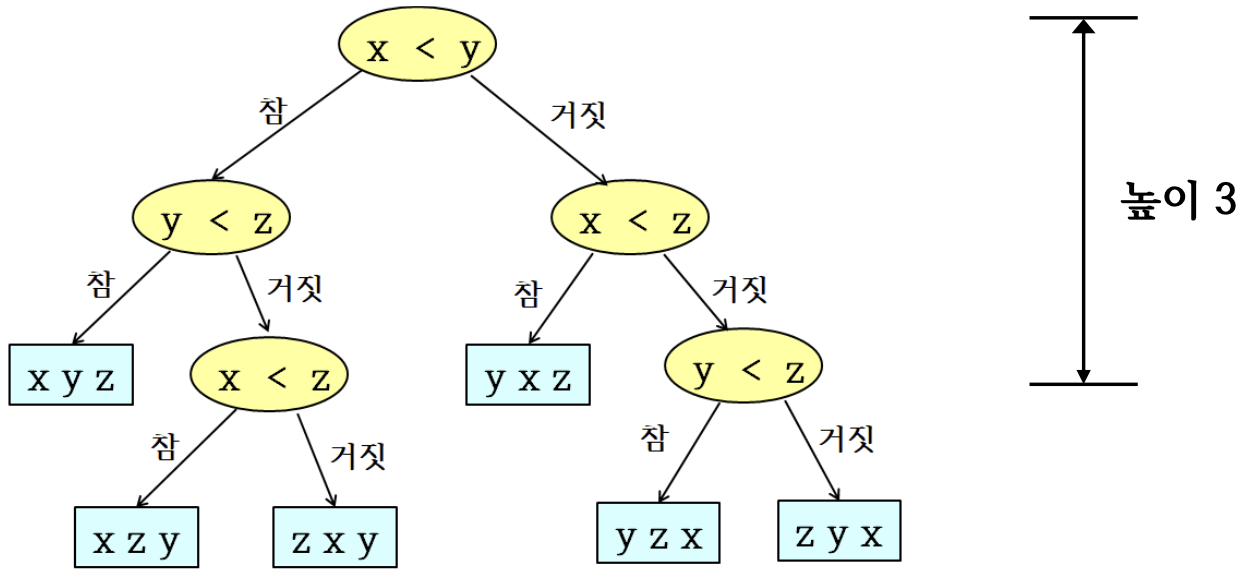
n개의 서로 다른 숫자를 비교 정렬하는 결정 트리의 높이가 비교 정렬의 하한이다.

• $k$개의 리프가 있는 이진 트리의 높이는 $logk$보다 크다.
• 따라서 $n$!개의 리프를 가진 결정 트리의 높이는 $log(n!)$보다 크다.
• $log(n!) = O(nlogn)$이므로, 비교 정렬의 하한은 $O(nlogn)$
  • $n! >= (n/2)^{n/2}$이므로 $log(n!) >= log(n/2)^{n/2} = (n/2)log(n/2) = O(nlogn)$

즉, $O(nlogn)$보다 빠른 시간 복잡도를 가진 비교 정렬 알고리즘은 존재하지 않음 $\rightarrow \Omega(nlogn)$

---

6.7 Radix sort

• 숫자를 부분적으로 비교하며 정렬
• radix(기)는 특정 진수를 나타내는 숫자들
  • 10진수의 기는 0, 1, 2, ... , 9
  • 2진수의 기는 0, 1
• 기수 정렬은 제한적인 범위 내에 있는 숫자에 대해서 각 자릿수 별로 정렬하는 알고리즘

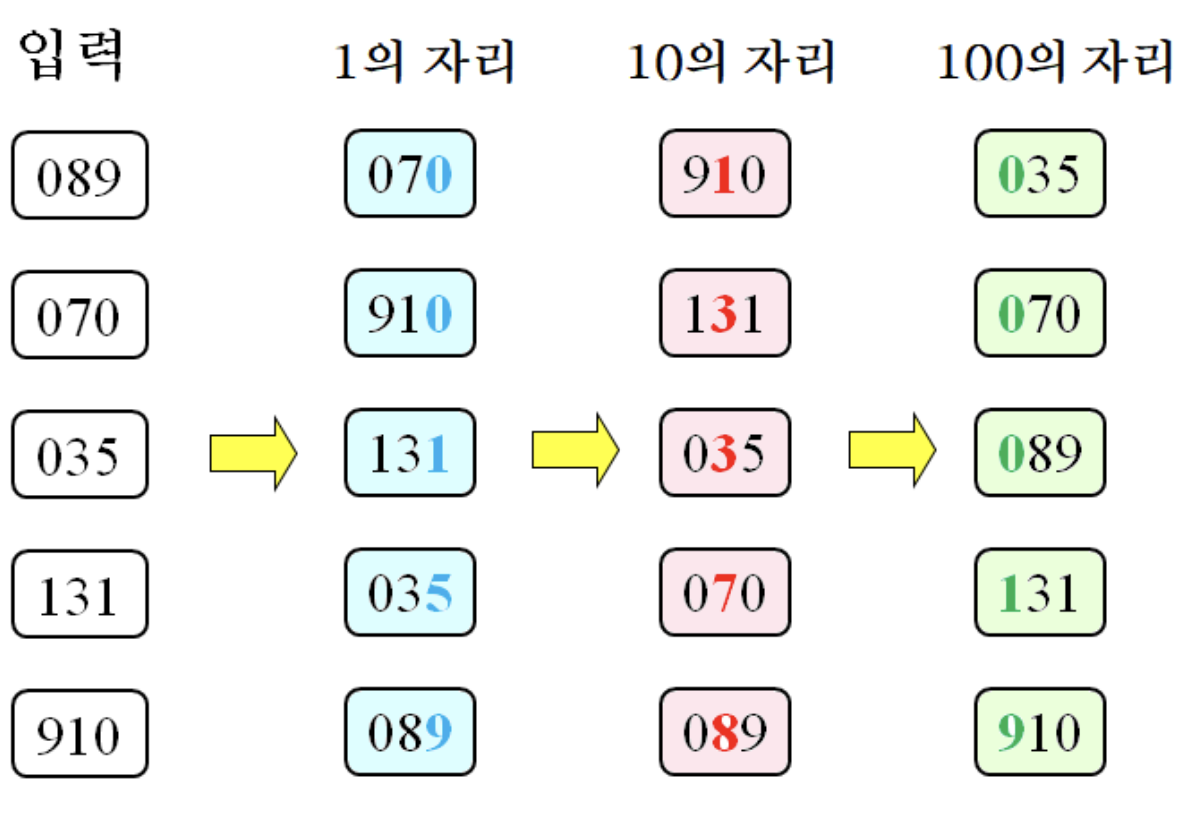
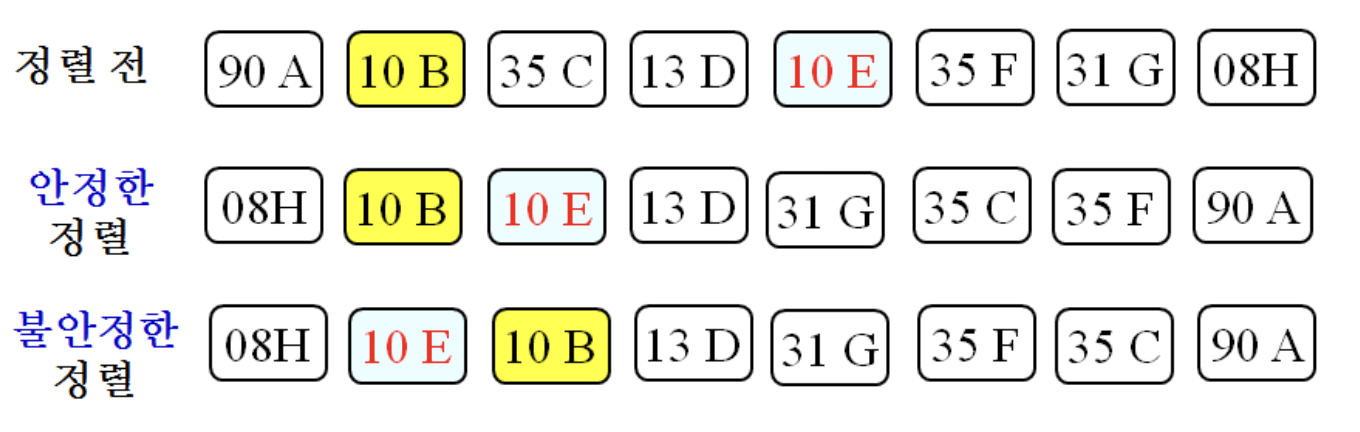
6.7.1 Stability

• 입력에 중복된 숫자가 있을 때, 정렬된 후에도 중복된 숫자의 순서가 입력에서의 순서와 동일할 때, 안정성을 가진다고 한다.

6.7.2 RadixSort()

• Input: n개의 r진수의 k자리 숫자
• Output: 정렬된 숫자

1. for i = 1 to k
2. $\,\,\,\,$ 각 숫자의 i 자리 숫자에 대해 안정한 정렬 수행
3. return A

6.7.3 LSD radix sort

• 1의 자리부터 k자리로 진행하는 경우, Least Significant Digit 기수 정렬 또는 Right-to-Left 기수 정렬이라고 부른다.

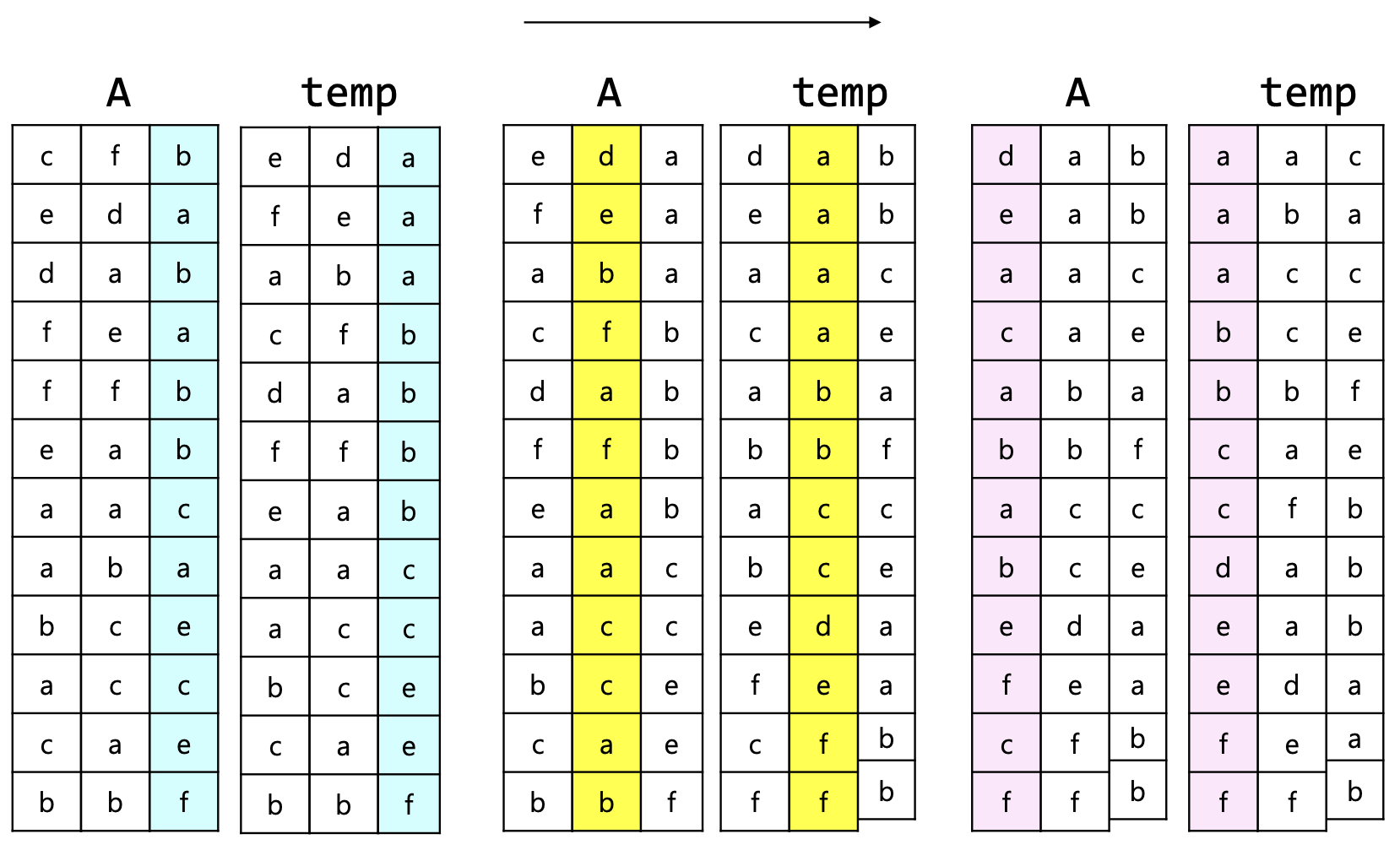
6.7.4 MSD radix sort

• k자리부터 1의 자리로 진행하는 경우, Most Significant Digit 기수 정렬 또는 Left-to-Right 기수 정렬이라고 부른다.

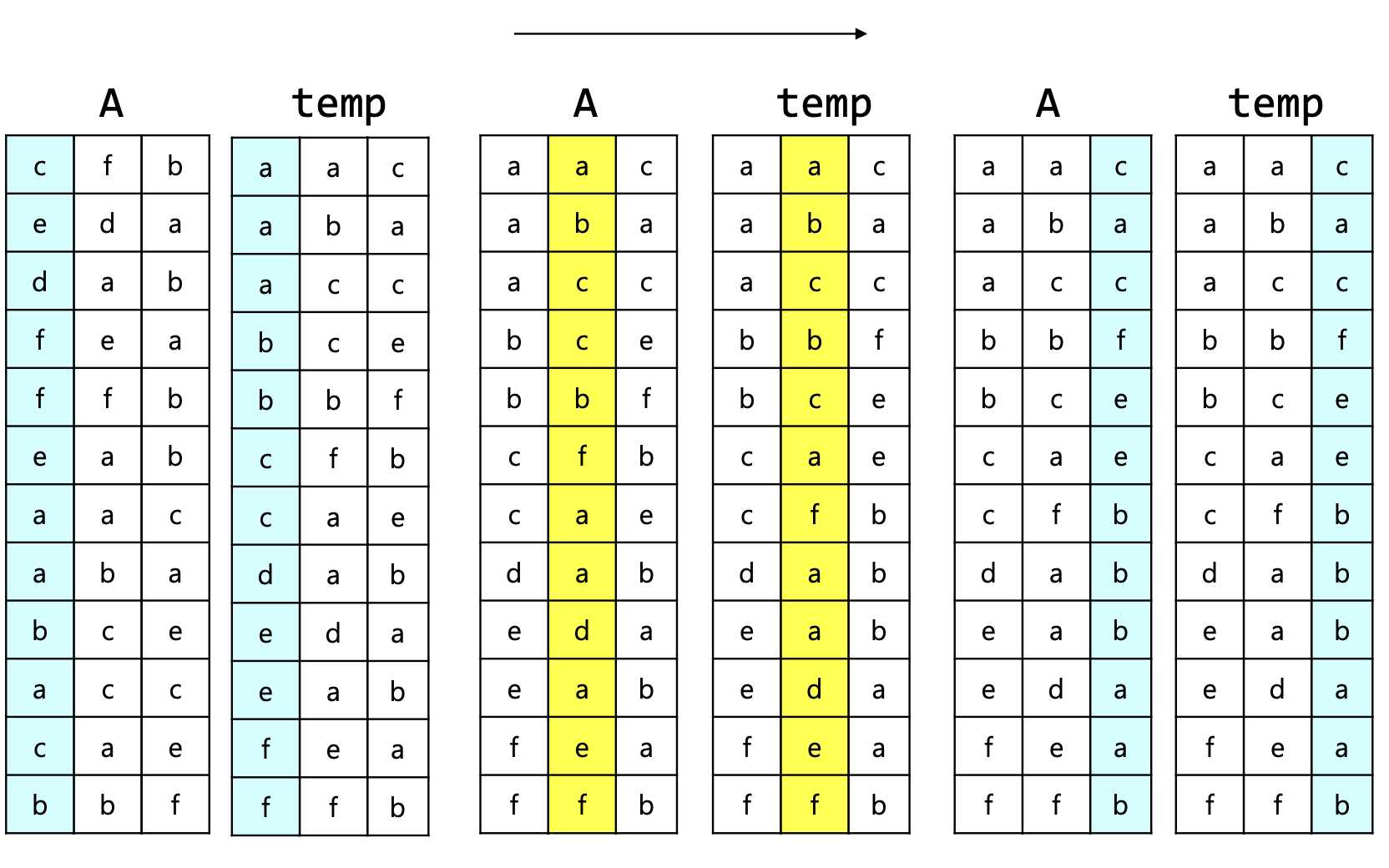
6.7.5 Time complexity

• for-loop가 k번 반복
  • k: 입력의 최대 자릿수
  • loop가 1회 수행될 때, n개의 숫자의 i자리 수를 읽으며, r개를 분류하여 개수를 세고, 그 결과에 따라 숫자가 이동 $\rightarrow O(n+r)$
• $O(k(n+r))$
  • k나 r이 입력 크기인 n보다 크지 않으면, 시간 복잡도는 $O(n)$

자릿수(r)가 몇 개인지 세는 것, 숫자들을 실제로 이동시키는 것이 각각 별도 단계로 처리된다.

6.7.6 Application

• 계좌 번호, 날짜, 주민등록번호 등 대용량의 상용 데이터베이스 정렬
• 랜덤 128비트 숫자로 된 초대형 파일의 정렬
• 지역 번호를 기반한 대용량의 전화 번호 정렬

다수의 프로세서들이 사용되는 병렬 환경에서의 정렬 알고리즘에 기본 아이디어로 사용

---

6.8 External sort

Internal sort

• 입력이 주기억 장치에 있는 상태에서 정렬

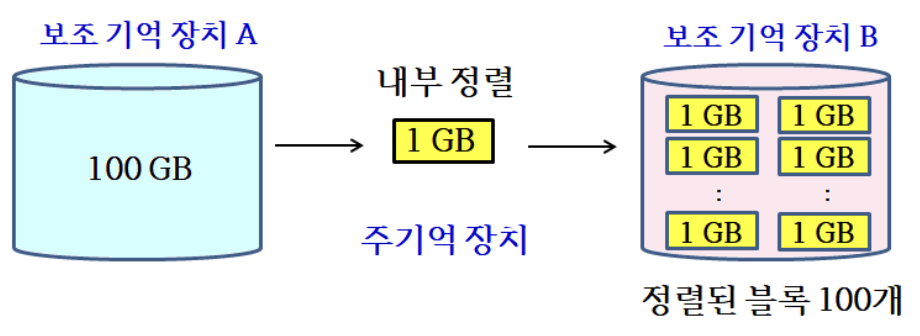
External sort

• 입력 크기가 매우 커서 읽고 쓰는 시간이 오래 걸리는 보조 기억 장치에 저장할 수밖에 없는 상태에서 정렬
• 주기억 장치의 용량이 1GB, 입력이 100GB라면, 어떤 내부 정렬 알고리즘으로도 직접 정렬 불가

• 100GB의 데이터를 1GB만큼씩 RAM으로 읽고, 퀵정렬과 같은 내부 정렬 알고리즘을 통해 정렬한 후, 다른 보조 기억 장치에 저장
• 원래의 입력이 100개의 정렬된 블록을 분할되어 보조 기억 장치에 저장

6.8.1 Sorted block's merge

• 정렬된 블록들을 반복적인 합병을 통해 하나의 정렬된 거대한 블록으로 만듦
  • 부분적으로 RAM으로 읽어, 합병을 수행하여 부분적으로 HDD에 쓰는 과정 반복

1GB 블록 2개가 합병되는 과정

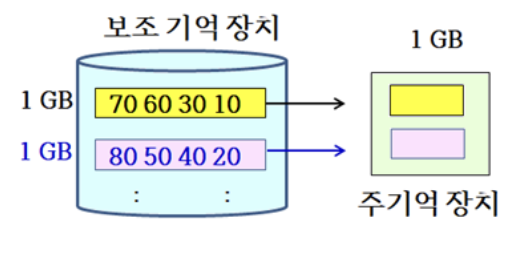
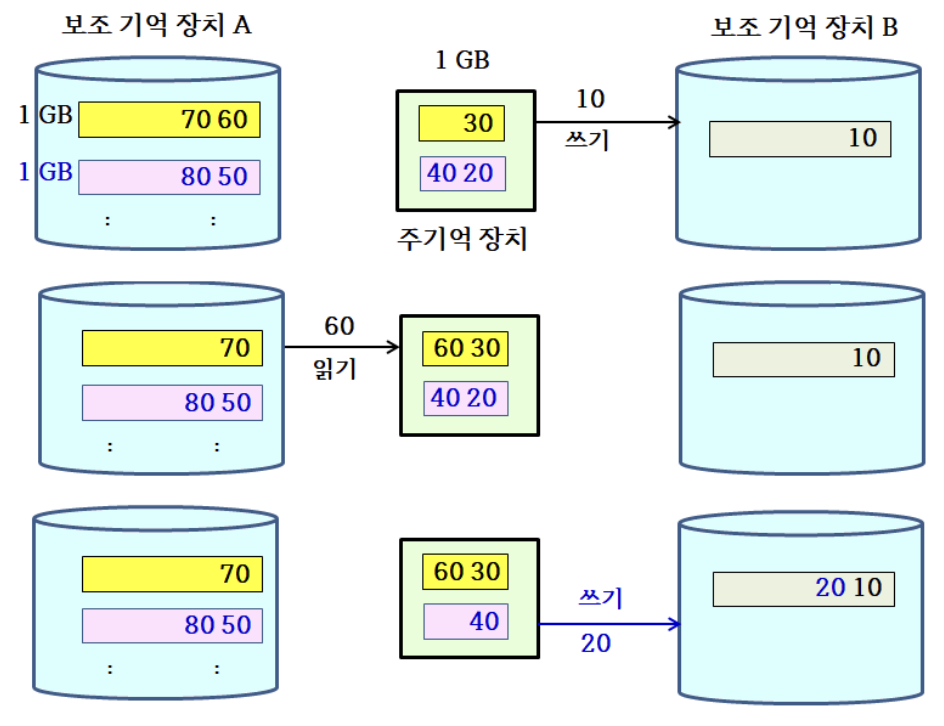
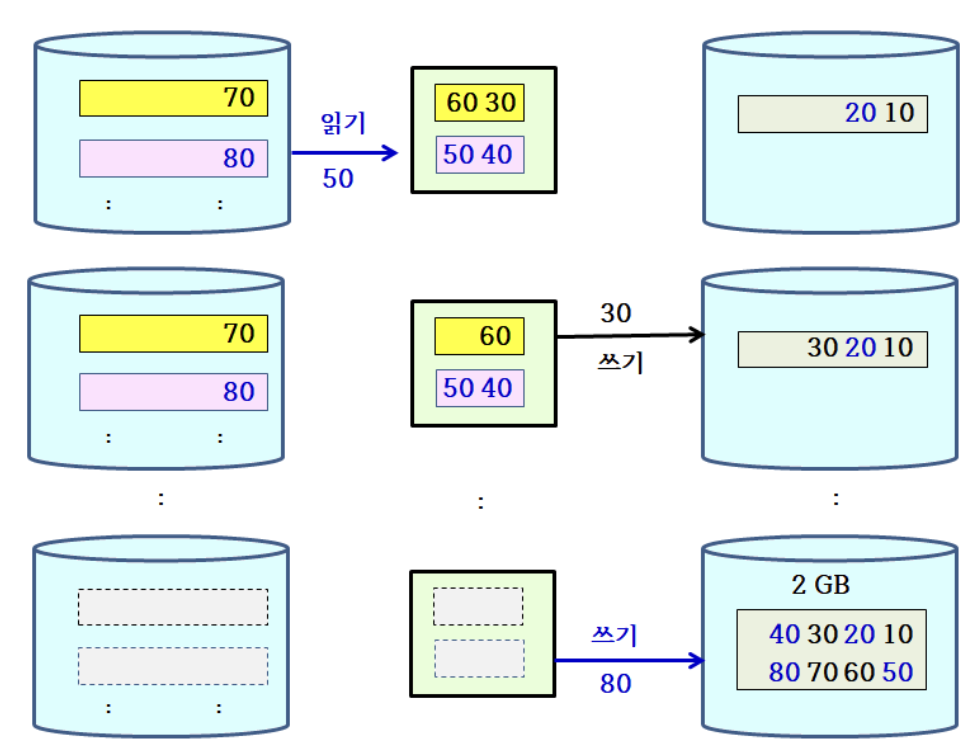
• 나머지 98개의 블록에 대해 이와 같이 49회를 반복하면, 2GB의 블록이 총 50개 생성
• 그 다음 2GB 블록 2개씩 짝을 지어 합병을 25회 반복하면, 4GB의 블록 25개 생성

계속 합병을 진행하면, 블록 크기가 2배로 커지고, 블록의 수는 1/2로 줄어들게 되어 결국에는 100GB 블록 1개가 남는다.

• 보조 기억 장치에서의 읽고 쓰기(I/O)를 최소화하는 것이 매우 중요
  • 보조 기억 장치의 접근 시간은 주기억 장치의 접근 시간보다 매우 오래 걸리기 때문

6.8.2 ExternalSort()

M은 주기억 장치의 용량, 입력이 저장된 보조 기억 장치 외에 별도의 보조 기억 장치 사용

• Input: 입력 데이터 저장된 입력 HDD
• Output: 정렬된 데이터가 저장된 출력 HDD

1. 입력 HDD에서 M만큼씩 데이터를 읽어, 내부 메모리에서 정렬한 뒤, 임시 HDD에 저장
2. while 임시 HDD에 저장된 블록 수 > 1
3. $\,\,\,\,$ 임시 HDD에서 블록을 2개씩 선택하여 주기억 장치로 읽고, 두 블록을 합병하여 출력 HDD에 저장
4. $\,\,\,\,$ 블록 수가 홀수일 경우 마지막 블록은 그대로 출력 HDD에 저장
5. $\,\,\,\,$ 입력/출력 HDD의 역할을 바꾼다.
6. return 출력 HDD

6.8.3 Procedure

128GB 입력과 1GB의 주기억 장치

• 1GB의 정렬된 블록 128개를 별도의 HDD에 저장
• 2GB의 정렬된 블록 64개가 출력 HDD에 생성
• 4GB의 정렬된 블록 32개가 출력 HDD에 생성
  ...
• 128GB의 정렬된 블록 1개가 출력 HDD에 생성
• 출력 HDD 리턴

6.8.4 Time complexity

전체 데이터를 몇 번 처리(읽고 쓰기)하는가를 가지고 시간 복잡도 측정

• Pass: 전체 데이터를 1회 처리
  • line3에서는 전체 데이터를 입력 HDD에서 읽고 합병하여 출력 HDD에 저장 = 1 pass
• 입력 크기 N, 메모리 크기 M, line3이 수행될 때마다 블록 크기 $2^kM$으로(2배) 증가
• 마지막 1개의 블록 크기가 $2^kM$이면, 이 블록은 입력 전체가 합병된 결과를 가지므로, $2^kM = N$
  • k는 while-loop가 수행된 횟수
    • $2^k = N/M$
    • $k = log_2(N/M)$
  • $O(log(N/M))$

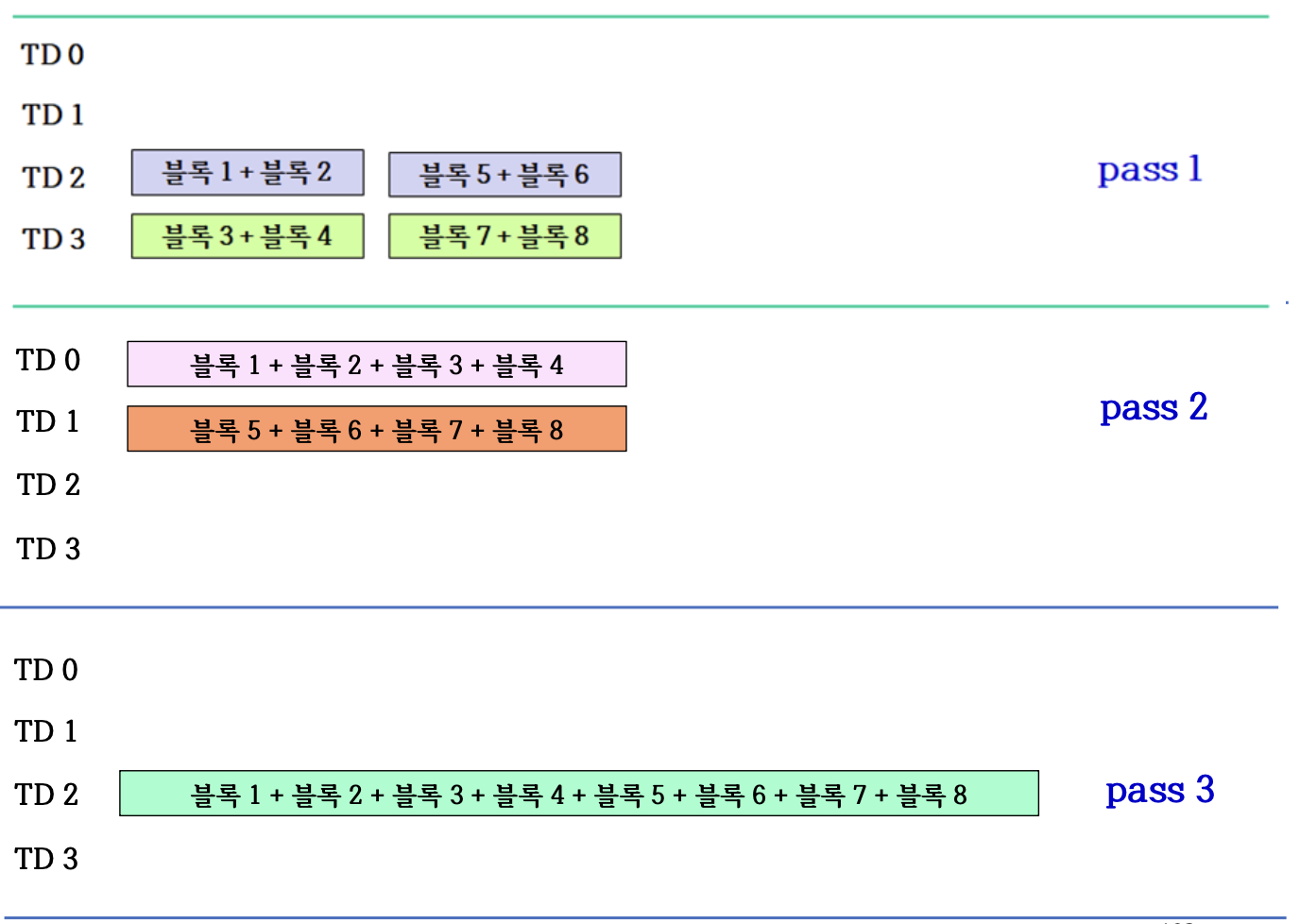
6.8.5 2-way 합병

• 하나의 보조 기억 장치에서 2개의 블록을 동시에 주기억 장치로 읽어 들일 수 있다는 가정
• Tape Drive 저장 장치는 순차적으로 읽고 쓰는 장치로, 2개의 블록을 동시에 주기억 장치로 읽어 들일 수 없다.

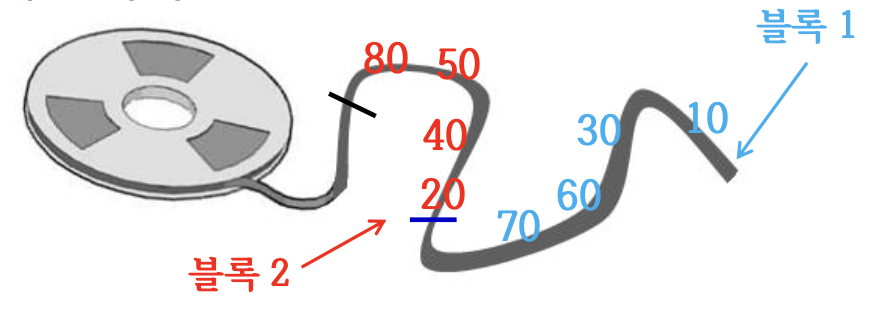
• 블록 1이 [10 30 60 70], 블록 2가 [20 40 50 80]로 두 블록을 합병하려면 블록 1의 10을 읽고, 블록 2의 20을 읽어서 비교해야 함
• 테이프를 한쪽 방향으로만 테이프가 감기므로, 합병하려면 블록 2의 20을 읽은 후 다시 되감아 블록 1의 두 번째 숫자인 30을 읽을 수 없다.

$\rightarrow$ line3에서 2개의 블록을 읽어 합병하면서 만들어지는 블록들을 2개의 저장 장치에 번갈아 저장

6.8.6 Procedure of 2-way

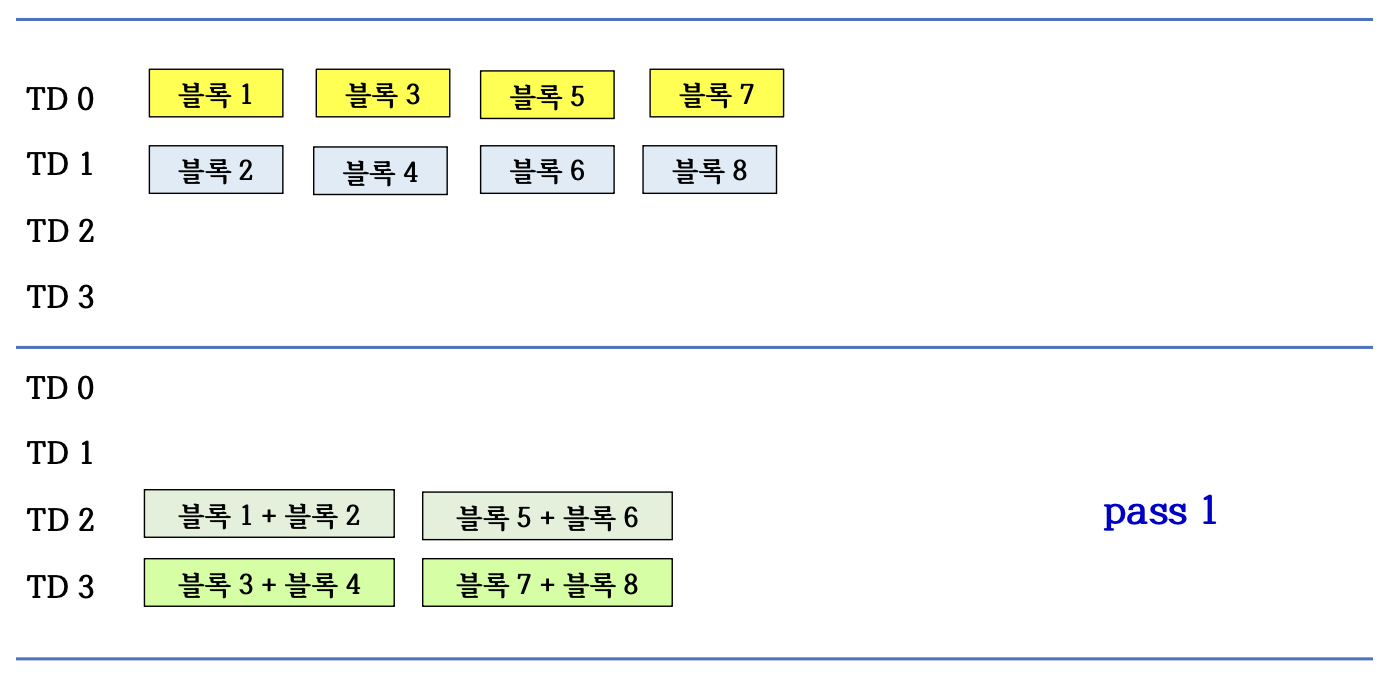
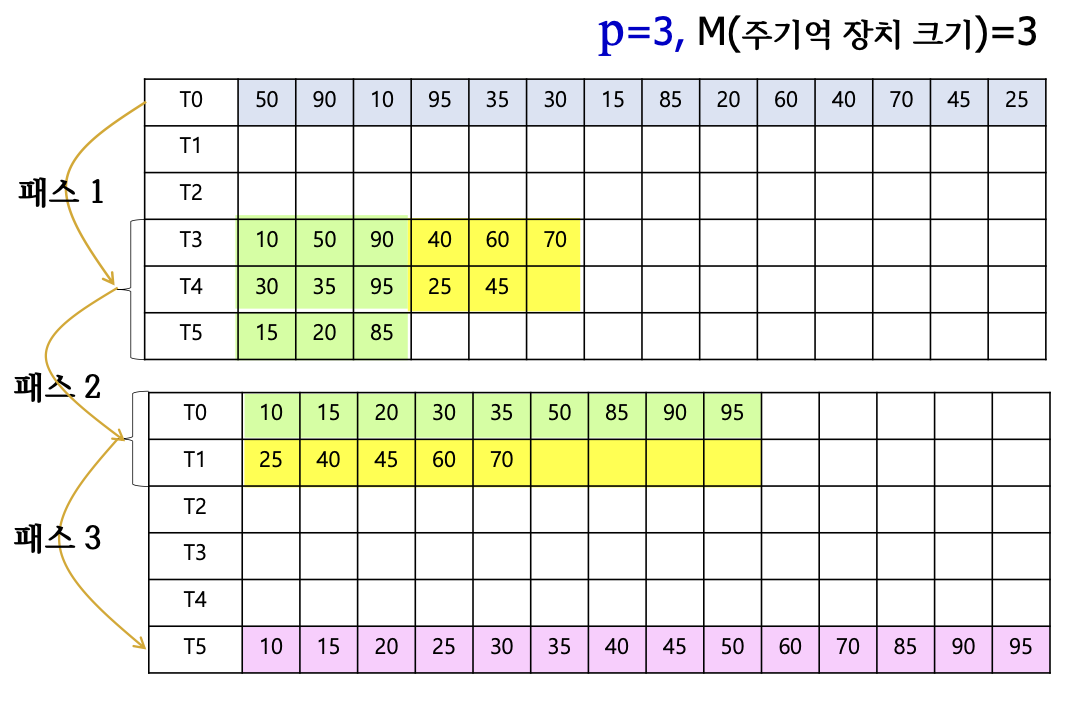
6.8.7 Multi-way merge

• 2-way 합병보다 빠름
• 시간 복잡도는 $O(log_p(N/M)$
• 그러나 2p개의 보조 기억 장치 필요

1. P-way merge

2. Polyphase merge

• (p+1)개의 보조 기억 장치만 가지고 p-way 합병
• M = 주기억 장치 크기
• 입력을 정렬된 크기가 M인 $F_n$개의 블록 생성
  • $F_n$은 피보나치 수(fixed value), 입력으로 $F_n$개를 만들 수 없으면 입력 데이터보다 매우 큰 데이터로 블록을 채움

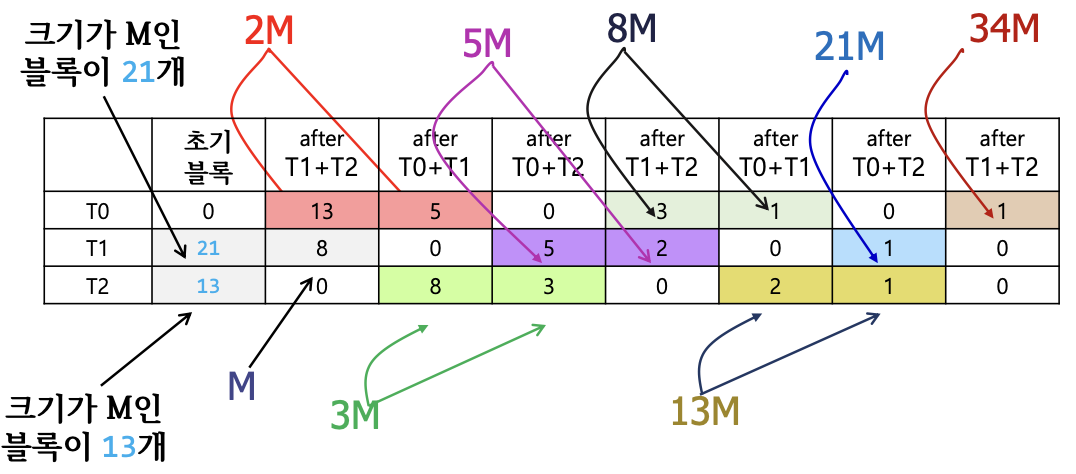
• p = 2일 때, $F_{n-1}$과 $F_{n-2}$로 나누어 블록들을 2개의 디바이스에 저장
• 입력 2개, 출력 1개로 총 3개의 HDD 사용

크기가 M인 블록이 대략 30개쯤 있다고 가정하면, 가장 가까운 큰 수인 34를 채택한다. $F_9$ = 34 = 21 + 13로 초기에 블록을 21개와 13개로 나눈다. 크기가 피보나치 항에 맞춰 증가하는 것을 확인할 수 있다.

총 패스 수 = 1 + (n-2) = 1 + (9-2) 패스
첫 패스 1 + 피보나치 항 2개를 제외하면 1 + (n-1)번의 패스를 반복한다.

6.8.8 Application

• 물품/재고/인사 DB 갱신
• 통신 회사의 전화번호 정렬
• 프로세스 스케줄링
• 그리디 알고리즘
• 근사 알고리즘 등