Algorithm
1.1. Algorithm

9세기경 페르시아 수학자인 알콰리즈미의 이름으로부터 유래 최초의 알고리즘: BC 300년 경 유클리드의 GPD 알고리즘 문제를 해결하기 위한 단계적인 절차 단계적인 절차를 따라 하면 요리가 만들어지듯이, 알고리즘도 단계적인 절차를 따라 하면 주어진 문제의 해를 찾는다
2.2. What is Algorithm?
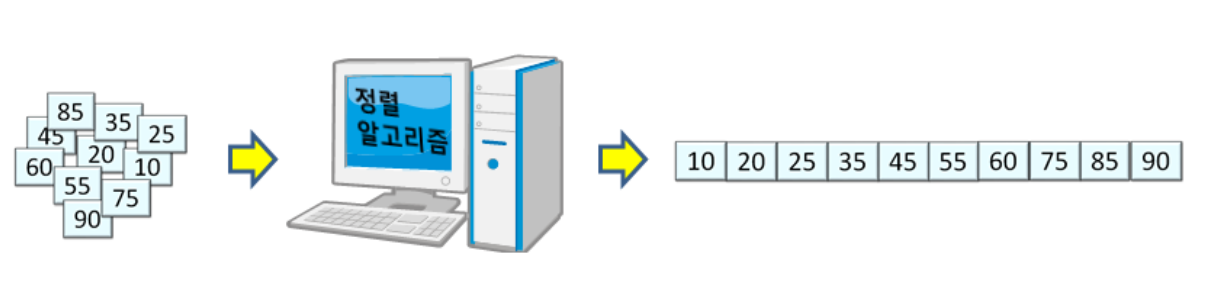
컴퓨터 문제를 해결하는 단계적 절차, 방법 알고리즘에는 입력이 주어지고, 알고리즘은 수행한 결과인 해를 출력한다. 정확성 주어진 입력에 대해 올바른 해 제공 수행성 각 단계는 컴퓨터에서 수행 가능해야 함 유한성 유한 시간 내에 종료되어야 함 효율성 효율적일수록 그 가
3.3. Divide and conquer algorithm (1)
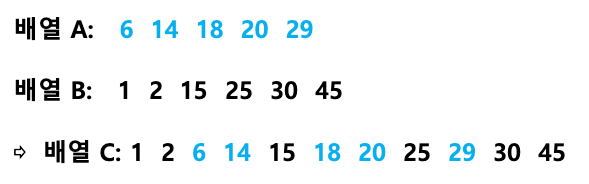
3. 분할 정복 알고리즘 주어진 문제의 입력을 분할하여 문제를 해결(정복)하는 방식의 알고리즘 분할(1)한 입력에 대하여 동일한 알고리즘을 적용하여 해 계산(2) 이들의 해를 취합(3)해 원래 문제의 해를 얻음 부분 문제와 부분 해 분할된 입력에 대한 문제를
4.3. Divide and conquer algorithm (2)
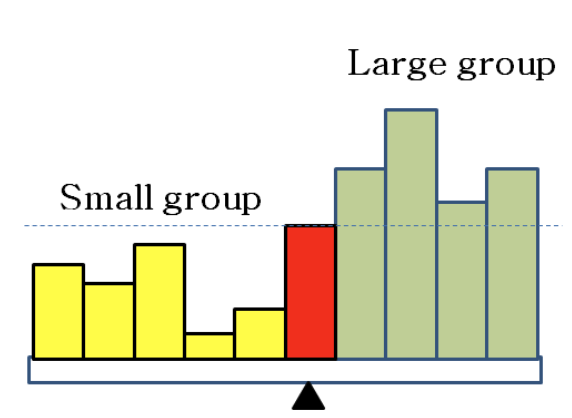
선택 문제는 n개의 숫자들(not 정렬) 중에서 k번째로 작은 숫자를 찾는 문제이다. 최소 숫자 숫자를 k번 찾는다. $O(n) \\times k = O(kn)$단, 최소 숫자를 찾은 뒤에는 입력에서 최소 숫자 제거 숫자들을 정렬한 후, k번째 숫자를 찾는다. 퀵 정
5.4. Greedy Algorithm(1)

4.0 Greedy Algorithm 최적화 문제를 해결하는 알고리즘 가능한 해들 중에서 가장 좋은(최대 or 최소) 해를 찾는 문제 욕심쟁이 방법, 탐욕적 방법, 탐욕 알고리즘 (입력) 데이터 간의 관계를 고려하지 않고 수행 과정에서 '욕심 내어' 최솟값 또는 최
6.4. Greedy Algorithm(2)

주어진 가중치 그래프에서 어느 한 출발점에서 또 다른 도착점까지의 최단 경로를 찾는 문제 Dijkstra Algorithm 최단 경로를 찾는 가장 대표적인 알고리즘 최단 거리가 확정되지 않은 정점들 중 출발점에서 가장 가까운 점을 선택해 최단 거리로 확정Input: 가
7.5. Dynamic Programming (1)
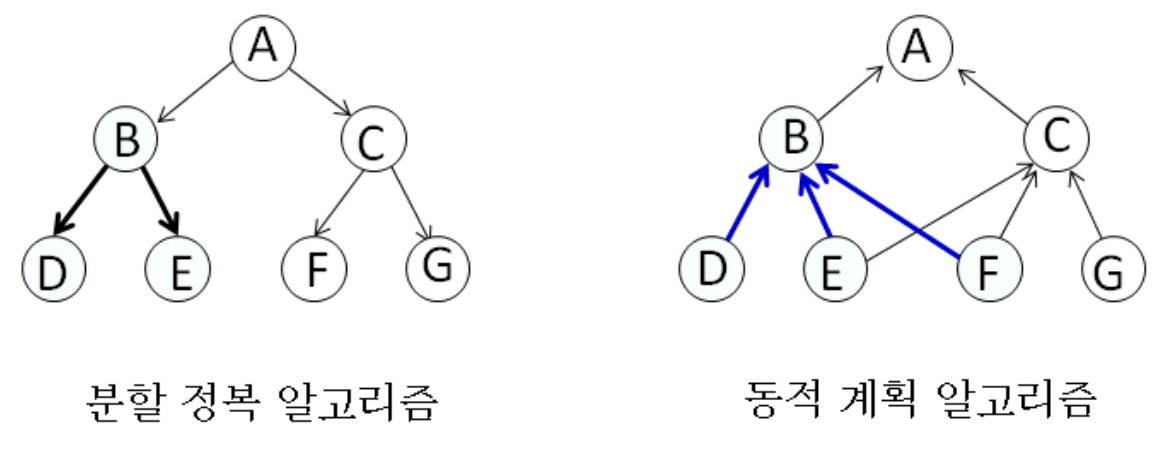
Dynamic Programming Algorithm 입력 크기가 작은 부분 문제들을 해결한 후에 그 해들을 이용하여 보다 큰 크기의 부분 문제들을 해결해 최종적으로 원래 주어진 입력의 문제를 해결 5.1 DP vs Divide and Conquer Divide an
8.5. Dynamic Programming (2)

5.3 Edit Distance 삽입(insert), 삭제(delete), 대체(substitute) 연산을 사용하여 문자열 $S$를 수정하여 다른 문자열 $T$로 변환하고자 할 때 필요한 최소의 편집 연산 횟수 1. 'strong' $\rightarrow$ 'st
9.5. Dynamic Programming (3)
5.4 Knapsack $n$개의 물건과 각 물건 $i$의 무게 $wi$와 가치 $vi$가 주어지고 배낭의 용량이 $C$일 때, 배낭에 담을 수 있는 물건의 최대 가치는? 단, 배낭에 담은 물건의 무게의 합이 $C$를 초과하지 말아야 하고, 각 물건은 1개씩만 있다.
10.6. Sort Algorithm (1)

정렬 알고리즘은 크게 2가지로 나눌 수 있다. 입력의 크기가 주기억 장치(RAM)의 공간보다 크지 않은 경우에 수행되는 정렬 버블 정렬, 선택 정렬, 삽입 정렬, 합병 정렬, 퀵 정렬, 힙 정렬, 쉘 정렬, 기수 정렬, 이중 피봇 퀵정렬, Time sort 대표적인 알
11.6. Sort Algorithm(2)

6.5 Heap sort 6.5.1 Binary heap 힙 조건을 만족하는 Complete binary tree 힙 조건: 각 노드의 우선 순위가 자식 노드의 우선 순위보다 높다. Maximum heap: 가장 큰 값이 루트에 저장 Minimum heap: 가장
12.7. NP-complete problem

7.1 Classification of problems 7.1.1 Deterministic vs. Non-Deterministic Deterministic One possible option at each decision step E.g., Dijkstra algori
13.8. Approximation Algorithm (1)

8.0 Approximation Algorithm 8.0.1 Strategy of Problem Solving If a target problem is easy Find an algorithm working in polynomial time Otherwise Do no
14.8. Approximation Algorithm (2)

8.4 Task Scheduling Goal Minimize the time of running all tasks Condition N tasks given T = {$ti$ | $ti$ = required time to finish task i, i = 1, 2,
15.9. Search Algorithm (1)

9.0 Search Algorithm Strategy Too complex problem No polynomial time algorithm Approximation Proof Too exhaustive and not very useful Difficult to g
16.9. Search Algorithm(2)

Find the probable solution first If we find a solution, go to the next probable "state" $\\rightarrow$ a partial solution 항상 부분해들을 체계적으로 탐색하고 bound를 p