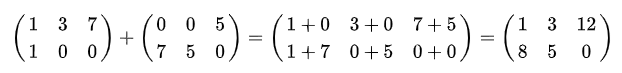[기초 수학] 행렬은 뭔가요?

교육 과정 개편으로 인해

저는 행렬을 배우지 못해

이번에 처음 접하게 되었는데요....

처음이라 잘 모르겠지만 천천히 알아가보겠습니다

행렬

벡터는 숫자를 원소로 가지는 1차원 배열이라면

행렬(matrix)은 행(row)벡터를 원소로 가지는 2차원 배열입니다

행렬 = 행(row) + 열(column)

$X$ $=$ $\begin{bmatrix} \mathbf x_{1} \\ \mathbf x_{2} \\ \vdots \\ \mathbf x_{n} \end{bmatrix}$ $=$$\begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1m} \\ x_{21} & x_{22} & \cdots & x_{2m} \\ \vdots & \vdots & & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{nm} \end{bmatrix}$

행렬의 특정 행(열)을 고정하면 행(열)벡터라고 부릅니다

$x_{11}$ 부터 $x_{1n}$까지를 나타내는 $\mathbf x_{1}$은 행벡터,

$x_{11}$ 부터 $x_{m1}$까지는 열벡터라고 할 수 있습니다

---

벡터의 전치행렬

전치행렬(transpose matrix)은 행과 열의 인덱스가 바뀐 행렬을 말합니다

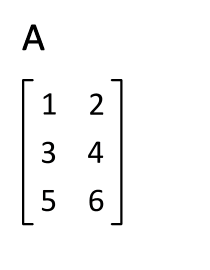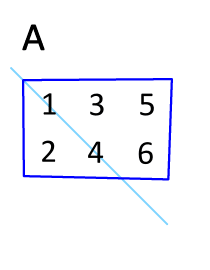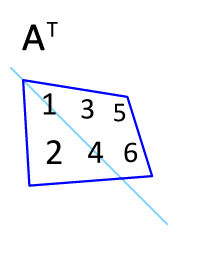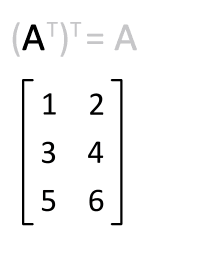
위의 $X$의 전치행렬은 다음과 같습니다

$X^T$ $=$ $\begin{bmatrix} x_{11} & x_{21} & \cdots & x_{n1} \\ x_{12} & x_{22} & \cdots & x_{n2} \\ \vdots & \vdots & \nearrow\swarrow & \vdots \\ x_{1m} & x_{2m} & \cdots & x_{nm} \end{bmatrix}$

원래 n개의 행과 m개의 열로 이루어진 경우

m개의 행과 n개의 열로 이루어진 행렬로 바뀌게 됩니다

이러한 전치행렬은 행렬의 연산에 굉장히 많이 사용됩니다

---

행렬을 이해하는 방법 (1)

벡터가 공간에서 한 점을 의미한다면

행렬은 여러 점들을 나타냅니다

행렬의 행벡터 $\mathbf x_{i}$는 $i$번째 데이터를 의미하고

행렬의 $x_{ij}$는 $i$번째 데이터의 $j$번째 변수의 값을 가리키게 됩니다

$X$ $=$$\begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1m} \\ x_{21} & x_{22} & \cdots & x_{2m} \\ \vdots & \vdots & x_{ij} & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{nm} \end{bmatrix}$

---

행렬의 연산

행렬끼리 같은 모양을 가지면 덧셈, 뺄셈을 계산할 수 있습니다

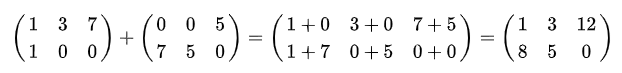
행렬의 성분곱과 스칼라곱은 벡터와 동일합니다

$X \odot Y$ $=$ $\begin{bmatrix} x_{11} y_{11} & x_{12} y_{12} & \cdots & x_{1m} y_{1m}\\ x_{21} y_{21} & x_{22} y_{21} & \cdots & x_{2m} y_{2m}\\ \vdots & \vdots & & \vdots \\ x_{n1} y_{n1} & x_{n2} y_{n1} & \cdots & x_{nm} y_{nm} \end{bmatrix}$


$\alpha X$ $=$$\begin{bmatrix} \alpha x_{11} & \alpha x_{12} & \cdots & \alpha x_{1m} \\ \alpha x_{21} & \alpha x_{22} & \cdots & \alpha x_{2m} \\ \vdots & \vdots & & \vdots \\ \alpha x_{n1} & \alpha x_{n2} & \cdots & \alpha x_{nm} \end{bmatrix}$

행렬 곱셈

하지만 행렬은 벡터와 큰 차이점을 하나 가지고 있는데요

행렬 곱셈은 벡터와 조금 다른 식으로 계산됩니다

행렬 곱셈(matrix multiplication)은

$i$번째 행벡터와 $j$번째 열벡터 사이의 내적을

성분으로 가지는 행렬을 계산합니다

$XY$ $=$ $\left(\sum\limits_{k}{x_{ik}\ y_{kj}}\right)$

그래서 행렬곱은 $X$의 열의 개수와 $Y$의 행의 개수가 같아야 합니다

---

행렬을 이해하는 방법 (2)

앞에서는 행렬을 데이터들의 모임

즉, 어떤 한 공간 상에서의 점들의 모임으로 설명했는데

이는 행렬을 이해하는 1가지 방법이고

2번째 방법을 알아보겠습니다


행렬은 벡터공간에서 사용되는 연산자(operator)로 이해할 수 있습니다

$z_i$ $=$ $\sum\limits_{j}{a_{ij}\ x_{j}}$

$\begin{bmatrix} z_{1} \\ z_{2} \\ \vdots \\ z_{n} \end{bmatrix}$ $=$ $\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1m} \\ a_{21} & a_{22} & \cdots & a_{2m} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nm} \end{bmatrix}$ $\begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{m} \end{bmatrix}$

$A$라는 행렬과 $X$라는 벡터를 곱하게 되면

$Z$라는 새로운 열벡터가 나오게 되는데

결론적으로 $Z$와 $X$라는 두 벡터를 $A$라는 행렬을 통해서 이어줄 수 있습니다

이처럼 이어주는 함수의 역할을 연산자로 이해할 수 있습니다

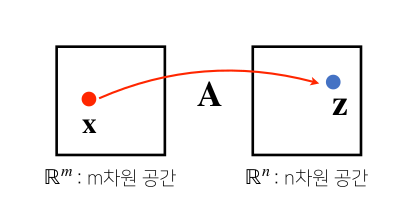
행렬을 이용해서 우리는 두 벡터를 연결해줄 수 있고

m차원 공간상에 존재하는 벡터를

다른 n차원 공간상의 벡터로 맵핑하는 연산자로 사용할 수 있습니다

이러한 행렬곱을 이용해서

주어진 데이터에서 패턴을 추출 및 압축을 할 수 있습니다

---

역행렬

어떤 행렬 $A$의 연산을 거꾸로 되돌리는 행렬을

역행렬(inverse matrix)이라 부르고 $A^{-1}$로 표기합니다

역행렬은 행과 열의 수가 같고

행렬식(determinant)이 0이 아닌 경우에만 계산할 수 있습니다

$AA^{-1}$ $=$ $A^{-1}A$ $=$ $I$

여기서 $I$는 항등행렬로

임의의 벡터 또는 행렬을 곱했을 때

자기 자신이 나오는 행렬을 의미합니다

$I$ $=$ $\begin{bmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & 1 \end{bmatrix}$

만약 역행렬을 계산할 수 없다면?

유사 역행렬(pseudo-inverse) 또는 무어-펜로즈(Moore-Penrose) 역행렬 $A^+$을 이용합니다

행과 열의 숫자가 달라도 역행렬과 완전히 똑같진 않지만

역행렬과 유사한 기능을 하는 행렬을 사용할 수 있습니다

대신에 조심해야 하는 점은

만약 주어진 행렬의 행의 개수가 더 많은 경우와

열의 개수가 더 많은 경우의 계산 방식이 달라지게 됩니다

$n \geq m$ → $A^+ = (A^TA)^{-1}\ A^T$
$n \leq m$ → $A^+ = A^T(A\ A^T)^{-1}$

$n \geq m$ 이면 $A^+A = I$가 성립하고
$n \leq m$ 이면 $AA^+ = I$만 성립합니다

응용

연립방정식 풀이

$a_{11}x_1 + a_{12}x_2 + \cdots + a_{1m}x_m = b_1$
$a_{21}x_1 + a_{22}x_2 + \cdots + a_{2m}x_m = b_2$
$\begin{matrix} & & & & & &\vdots \end{matrix}$
$a_{n1}x_1 + a_{n2}x_2 + \cdots + a_{nm}x_m = b_n$

위의 연립방정식을

행렬을 사용하여 표현하면 → $A\,\mathbf x = \mathbf b$

$n \leq m$ 이면 무어-펜로즈 역행렬을 이용하여 해를 하나 구할 수 있습니다

$\mathbf x = A^+\mathbf b$
$\,\,\,\,\,$$=$ $A^T\,(A\,A^T)^{-1} \mathbf b$

선형회귀분석

방금처럼 변수의 개수(m)가 식의 개수보다(n) 많은 경우

연립방정식 문제를 풀 수 있습니다

만약에 변수의 개수(m)보다 식의 개수보다(n) 많은 경우

즉, 데이터가 변수의 개수보다 많은 경우($n \geq m$)

선형회귀분석에서 많이 보게 되는 상황입니다

이런 문제도 앞에서 했던 것처럼 유사 역행렬을 이용해서

데이터를 표현하는 선형모델을 해석했을때

이 모델에 해당하는 선형회귀식을 찾을 수 있습니다

참고자료

[부스트코스] 인공지능 기초 다지기 (AI Basic) - 행렬이 뭐에요?
위키백과 - 전치행렬