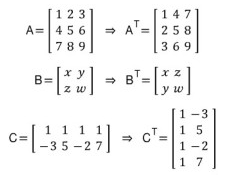
이 챕터는 혁펜하임의 강의를 정리하였습니다. (출처: https://www.youtube.com/watch?v=47axVfuf-Q0&list=PL_iJu012NOxdZDxoGsYidMf2_bERIQaP0&index=5)
전치 (Transpose)
전치 행렬은 쉽게 말해서 어떤 행려의 행과 열을 서로 맞바꾼 행렬을 전치행렬(transposed matrix)라고 한다. 전치는 행렬뿐만 아니라 Vector에도 적용할 수 있다 열벡터를 전치하면 행벡터가 되고 행벡터를 전치하면 열벡터가 된다.
정의
의 크기를 갖는 행렬 에대하여 의 크기를 갖는 행렬 로서 를 만족할 때 를 행렬 A의 '전치행렬'이라고 한다.
예시
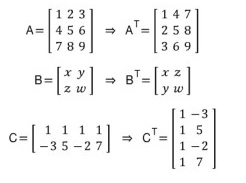
성질
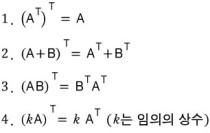
벡터의 내적과 정사영 (Dot Product and Projection)
벡터의 내적은 선형대수 여러 곳에 사용되는 핵심적인 개념이기 때문에 무조건 이해하고 넘어가야 한다. 그런데 단순히 수식만 암기하는 것이 아니라 이게 기하학적으로 어떤 의미를 지니는지를 이해하는게 더 중요하다. (공학은 이렇게 이해해도 되더라구 ㅇㅇ)
내적 정의
- 일반적 정의
그냥 복잡한 정의 말고 까놓고 말하면 성분끼리 곱하고 더한다. 벡터의 내적은 input으로 벡터가 들어가고 output으로 실수가 나온다.
벡터 a,b를 아래와 같이 정의하자.
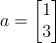
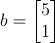
두 벡터 a,b의 내적은 다음과 같이 계산된다.
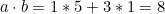
- 행렬 곱셈으로 정의 (매우 중요)
벡터의 내적을 전치와 행렬의 곱셈으로도 정의할 수 있다. (사실 벡터의 내적을 사용할때 이 방식을 많이 사용한다., 지난 시간에 행렬의 곱셈을 행벡터와 열벡터간의 내적이라고 말하였다.)
벡터의 내적은 다음과 같이 정의될 수 있다.
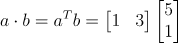
벡터의 크기
벡터의 크기를 정의하는 가장 간단한 방법은 피타고라스 빗변을 구하는 방식처럼 구하면 된다.

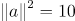
그런데 위 식을 벡터의 내적으로도 표현할 수 있다.
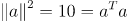
여기서 벡터 내적의 유용한 성질을 도출할 수 있다.
(중요) 자기자신의 내적은 크기의 제곱값이다 (Norm에 대한 설명은 다음 챕터에서 다루겠다.)
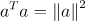
단위 벡터
단위벡터란 크기가 1인 벡터를 말한다
어떻게 만들까? 간단하다. 만약 벡터 a를 단위벡터로 만들고 싶으면 자기 자신의 크기를 나눠주면 된다.(Normalize)
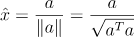
벡터 a의 크기 정의는 위 정의를 사용하였다.
내적은 정사영이다!!(Projection)
제2 코사인 법칙를 벡터로 유도하면 다음과 같이 벡터를 정의할 수 있다. (증명은 구글에 치면 널렸다.)
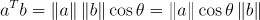
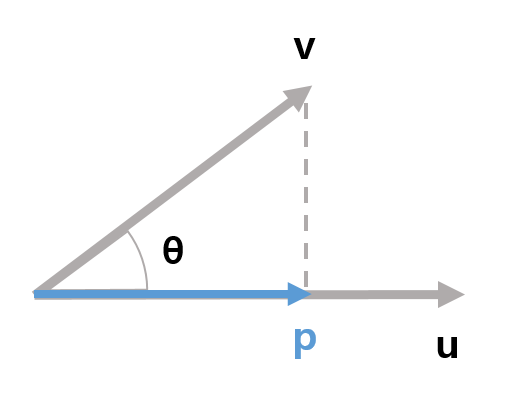
위 개념을 통해 내적은 기하학적으로 이해하면 두 벡터가 있을 때 한 벡터 위로 내린 정사영과 관계 있다. (위 수식을 보면 알겠지만 어느 벡터 위로 정사영을 할지는 상관없다. 정사영은 그림자라고 직관적으로 이해하자)
정사영된 벡터의 Norm과 기준 벡터의 Norm을 곱한것이 내적 값이다. 이것은 내적이 닮은 정도를 표현한다를 이해할 때 중요하게 사용되는 아이디어다.
내적은 닮은 정도를 나타낸다.
흔히 벡터의 내적을 왜 사용하냐고 물어보면 벡터간의 닮은 정도를 나타내기 위함이라고 한다. 그러면 왜 내적은 닮은 정도를 나타낼까? 그것은 벡터를 정사영이라고 생각하면 쉽게 이해할 수 있다.

벡터 u를 고정하고 벡터 v만 움직인다고 가정했을때 내적값은 벡터 v와 벡터 u의 각도로만 결정된다. 내적값을 계산해보면 0도에서 가장 크고 90도에서 9이며 180도일때 가장 값이 낮다는 걸 확인할 수 있다.
정사영 관점에서 내적을 또다르게 바라보면 u에 정사영된 그림자의 길이가 내적값을 결정하고 있다 각이 높아질수록 그림자 길이가 짧아지고 90도가 될때 그림자의 길이가 0이 된다. 그러다 다시 각이 커져 180도가 되면서 그림자 길이는 길어지지만 방향이 반대이기 때문에 음수가 된다. 내적값이 최대가 되는 때는 v와 u가 같은 방향일때다
벡터의 닮은 정도를 "같은 방향을 바라보고 있는가"로 정의할 수 있고 그 정도는 내적으로 계산할 수 있다. 같은 방향 0도일때 두 벡터의 방향은 같고 동시에 내적값이 최대이다. 반면에 90도일때 두 벡터는 orthogonal하며 내적값이 0이고. 180도일때 두 벡터의 방향이 반대이며 내적값이 최솟값이다.
정사영된 벡터 구하기

u로 정사영된 벡터를 어떻게 구하면 될까? 수식은 복잡해 보이지만 아이디어는 매우 간단하다.
- 그림자의 크기를 구하고
- 그 그림자의 크기와 u의 단위벡터에 곱한다.
u의 단위벡터는 크기가 1이고 방향만 u와 같다.
1,2를 수식으로 표현하면
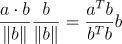
벡터의 Norm
Norm 이란 크기를 나타낸다.
보통 1차 Norm,2차 Norm을 많이 사용하고 p-Norm inf-Norm도 있다. 그냥 지수에 넣는 숫자에 따라 구분한다.
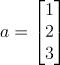
-
2-Norm
우리가 흔히 사용하는 Norm의 개념이다.
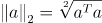
-
1-Norm
크기가 음수가 될 수 없기 때문에 절댓값을 씌운다.
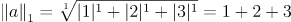
-
P-Norm
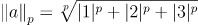
-
infinity norm
가장 큰 성분만 남기는 norm으로 adversarial attack에서 많이 사용하는 norm이다.
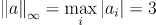
행렬곱셈
우리는 단순히 행렬 곱셈의 공식만 암기하는 것이 아니라 그것이 무엇을 의미하는지 Insight을 얻는데 집중할 것이다.
일반적 행렬곱
행렬의 곱셈 방식은 좀 독특하다.
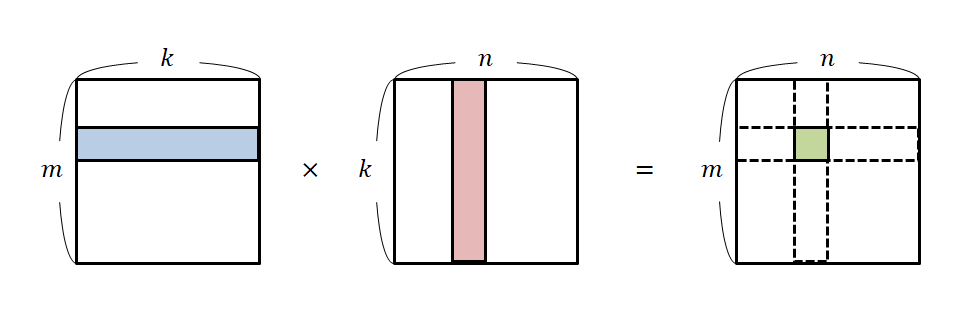
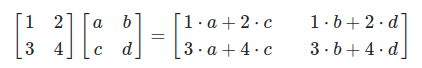
행렬곱의 이런 형태는 "행렬은 vector을 mapping하는 일종의 함수이고 행렬곱은 두 함수의 합성함수" 라는 아이디어를 받아들이면 된다.
행렬을 어떤 함수 라고 생각해보자.
이 함수는 2차원의 벡터를 받아 2차원의 벡터로 mapping하는 함수이다.
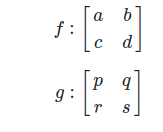
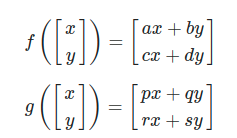
이때 두 함수 f,g의 합성함수는 다음과 같다.
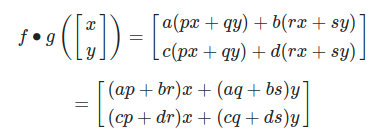
행렬의 곱은 함수의 합성함수이므로 행렬의 곱은 다음과 같이 표현할 수 있다.
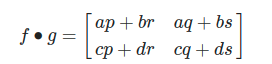
이제 왜 행렬의 곱이 이렇게 정의되었는지 알 수 있다.
하지만 중요한 건 저 공식 형태가 아니다.(저건 그냥 의미 몰라도 외우면 된다!!!
) 더 중요한 건 저 식으로부터 얻어야 하는
insight이다. 두 행렬의 곱 행태를 다시 관찰해보자.

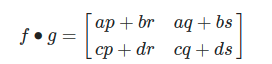
위 식으로부터 아래식을 보고 유추할 수 있는 것은
행렬곱의 각 원소값은 f의 열벡터와 g의 행벡터 각각의 내적을 표현하고 있다
즉, 일반적으로 이용하는 행렬곱의 관점은 행벡터와 열벡터같의 내적(inner product)을 계산함으로써 행렬곱이 이루어진다는 것을 알 수 있다. 이러한 행렬곱의 해석은 공분산을 구할 때 사용된다.
행렬곱은 열벡터의 선형결합
이번에는 행렬과 벡터의 곱에 대해 생각해보자.
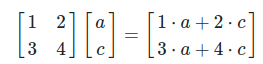
우리는 이 결과를 다르게 표현할 수도 있다.
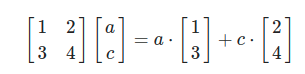
아까 우리는 벡터의 상수배와 벡터간의 합을 선형결합이라고 배웠다. 위 식은 행렬의 열벡터의 선형결합을 나타낸다. 즉 행렬의 곱을 열벡터의 선형결합으로 이해할 수 있다.
그러면 왜 이러한 해석이 중요할까? 아까 우리는 벡터 선형결합의 의미하는 것은 벡터 공간의 생성이라는 것을 배웠다. 행렬과 벡터의 곱이라는 수식이 우리에게 주는 깨달음은 주어진 열벡터들을 이용해 만들 수 있는 벡터공간(열공간,Column Space)이다.(행렬과 행렬의 곱은 행벡터와 열벡터의 내적)
처음 Systems of Linear Equation 수식을 예시로 들어보자.
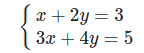
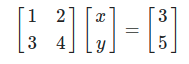
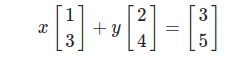
이 식이 우리에게 묻는 것을 위 열공간을 기반으로 번역하면
두 벡터 와 로 생성된 벡터공간 내에 벡터 가 존재하는가? 이다.
어렵네 좀더 쉽게 풀어 써보자
두 벡터 와 의 조합으로 가 만들어질 수 있는가?
이러한 관점으로 선형연립방정식의 해집합을 구한다 (우리가 원하는 연립방정식의 해를 구하는 Insight가 바로 이것이다.)
Span 과 Column space(열공간)
행렬곱 공부하면서 Linear Combination을 통해 Vector Space를 만든다라고 설명하였다.
여기서 Span이라는 개념을 모르고 넘어가면 곤란하다.
Span
-
Span이란 벡터들을 이용하여 온갖 선형결합을 통해 만들어진 Vector Space를 말한다.
-
영어로는 Set of vectors constructs of vector space by linear combination
-
쉽게 말해서 벡터 v1,v2,v3,...vn들의 가능한 모든 선형 조합들이 공간을 형성한다
-
예를 들어서 [1 0][0 1]2개의 벡터로 만들어질 수 있는 모든 선형결합의 결과물을 모으면 좌표평면이 되잖아? 그렇지 그러면 좌표평면은 Vector Space가 되는 것이다. (쉽쥬? 그냥 점을 모아서 진짜 공간을 만든다고 생각하자)
Column space
- 행렬의 열벡터들의 선형결합을 통해 만들어질 수 있는 모든 벡터들의 집합 (벡터 공간)
- 생각의 지평
아래 연립방정식을 Column space의 개념으로 이해하면 A의 열벡터로 만든 Column space에서 b라는 vector가 존재하냐 그것이 존재한다면 선형 결합의 coefficient를 구해라 (Vector x가 coefficient)
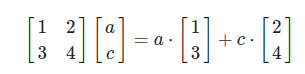
선형 독립과 기저 (Linear Independence)
선형결합에서 선형 독립이라는 개념은 매우 중요하고 이 개념은 기저러 확장된다. (단어가 조금 어렵게 보이지만 알고보면 별거 아니다.)
선형 독립
벡터 v1,v2,v3,...vn가 있다고 하자 그런데 이것들 조합(선형결합)으로 0을 만들고 싶다 ㅇㅇ 그런데
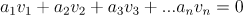
이때 가 모두 0이 되는것 말고는 값을 0벡터를 만들 수 없을때 벡터 을 선형 독립이라고 한다.
좀더 직관적으로 이해하면 어떤 vector도 다른 벡터의 결합으로 나타낼 수 없는 각자의 unique한 vector들만 있다면 그 벡터 집합은 linear Independence하다고 한다.
좌표 평면에 그냥 아무 벡터 합 그러니 (1,0)(0,1) 2개를 뽑아보자 (1,0)은 절대 (0,1)로 표현할 수 없고 (0,1)은 절대로 (1,0)로 표현할 수 없다. 이때 이 2 벡터는 선형독립이라고 한다.
(1,0)(0,1)(1,1)로 구성된 벡터 집합이 있다고 가정하자. (1,1)은 (1,1)=(1,0)+(0,1)로 표현할 수 있다. (1,1)은 unique하지 않다는 얘기!!
즉, (1,1)-(1,0)-(0,1)=0 으로 0벡터를 만들 수 있기 때문에 이 집합은 선형 종속이다.
기저 (Basis)
Basis: 어떤 공간을 이루는 필수적인 구성요소
뭔 개소리지?
Basis: 어떤 공간을 Span할 수 있는 선형독립인 벡터 집합
ㅅㅂ
Basis: 그러니깐 어떤 Vector 공간이 있을때 그 공간의 모든 벡터를 표현할 수 있는 (선형결합으로) 벡터 집합이 있다고
ㅇㅇ
Basis: 그러면서 이 벡터 집합이 선형독립(각자가 unique해서 서로가 서로를 정의할 수 없어)일때 Basis라고 하는거야
좀만 더 쉽게 설명
Basis: 2차원 좌표평면이 있을때 [1,0][0,1]로 구성된 집합이 있는데 이걸로 좌표평면 다 표현할 수 있지? 그리고 서로가 서로를 정의 못하니 선형독립이지? 그러면 이 집합은 기저야
ㅇㅎ
항등행렬,역행렬,직교행렬
항등행렬
항등행렬은 항등원의 행렬로 표현된 개념이다.
곱했을 때 자기자신이 튀어나올수 있도록
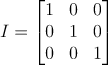
대각성분이 모두 1이고 나머지가 0인 정사각행렬
역행렬
곱해서 항등원이 나오도록 하는 역원의 개념을 행렬로 표현
즉 행렬을 곱해서 항등원이 나오도록 하는 행렬
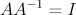
잠만 그럼 Ax=b라고 했을때 A역원 구해서 넘기면 되는거 아니야?
(세상일이 그리 간단하지가 않아 역행렬 없는 경우가 많다... 그래도 풀 수 있는 방법을 차후에 배울거)
대각행렬
대각성분 말고는 다 0 (항등행렬도 대각행렬이네?)
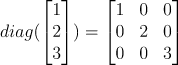
직교 행렬 (Orthogonal marix)
행렬들 column vector들이 서로 내적이 0이면서 크기가 1
직교 행렬은 그 성질 덕분에 계산이 편리하여 많이 사용한다.
무슨 성질? 직교 행렬의 역행렬은 그 행렬의 Transpose이다
행렬의 곱이 행벡터와 열벡터간의 내적이라고 배웠다 그런데 자기 자신의 Transpose와 곱한다면? 열벡터들간의 내적이 되는 것이다. 자기 자신과의 내적일때는 크기가 1이기 때문에 1이되고 나머지 성분과는 모두 Orthogonal하기 때문에 0이 되어 항등행렬이 만들어진다.
Rank (행렬의 계수)
랭크란? Column space의 Dimension
쉽게 말해서 행렬의 Column vector 집합에서 unique한 vector의 갯수 (다른 걸로 표현할 수 없는)== 행렬이 가지는 independent한 column의 수
존나 중요한성질
independent한 column의 수 = independent한 row의 수
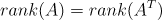
예시를 들어보자면
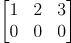
라는 행렬이 있을때 열벡터 [1 0]로 나머지 2개를 표현할 수 있다. 그러면 unique한 vector 1개이므로 rank가 1이다.
행벡터 또한 [1,2,3]로 [0,0,0]을 표현할 수 있기 때문에 rank가 1이다.
rank가 column수와 같다면 full column rank
rank가 row수와 같다면 full row rank
정사각 행렬인데 rank가 column row랑 같다면 그냥 full rank라고 한다.
Null Space(영공간)
Ax=0을 만족하는 x의 집합
행렬 A를 다음과 같이 정의할때
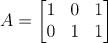
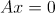
는 다음과 같이 column들의 선형결합으로 정의할 수 있다.
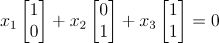
이때 null space x는
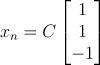
이고 rank는 column이 1개이므로 1이대
A의 rank는 [1 1]가 나머지 2개로 표현될 수 있기 때문에 rank가 2이다.
어 근데 원래 A의 rank하고 null space의 rank를 더하니 column의 갯수네?
여기서 중요한 성질이 나온다
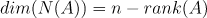
- Null space의 재밌는 성질
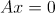
의 의미를 조금 기하학적으로 살펴보자 x를 null space의 집합이라고 하자. 우리는 행렬의 곱이 행벡터와 열벡터간의 내적이라고 알고 있다.
그러면 우리는 Null space는 행벡터와 수직이다라는 Insight를 얻을 수 있다.
결과적으로 Null space는 row space와 수직인 space이다
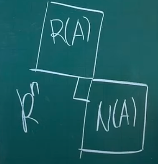
그러면
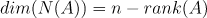 의 의미를 다시 생각해볼 수 있다.
의 의미를 다시 생각해볼 수 있다.
Ax=b의 해의 수 알아내기
다시 돌아가서 우리가 선형대수를 배우고 싶은 이유는 연립일차방정식을 풀기 위해서다. 정확히는 해집합을 구하기 위해서 해가 없을 수도 있고 1개일 수도 있고 무수히 많을 수도 있다. 풀기 전에 이 연립방정식이 저기서 어느 타입인지 판별하는 것은 매우 유용할 것이다.
full column rank 일때 : 해가 없거나 한개
만약 3X2 행렬 A가 있다고 가정하자.
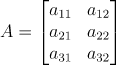
행렬곱을 열벡터들이 생성하는 벡터공간이라는 아이디어를 가져오면
A는 3차원 공간상에 만드는 평면이다. 그런데 3차원에는 평면이 무한이잖아?
그렇다면 Ax=b라고 했을때 b는 A평면에 있을 수 있고 없을 수 있다. 즉 b가 A평면 위에 있다면 해가 단 하나이고 만약 평면위에 없다면 해가 0이다 (평면위에 있다고 해도 표현할 수 있는 방식은 여러개일 수 있잖아? ㄴㄴ 기저로 표현할 수 있는 방식은 unique해요)
full column rank일때는 null space가 없기 때문에 해가 무한할 수 없다.
full row rank 일때 : 해가 무한하다.
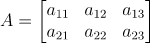
만약 A가 3X10의 행렬이가 rank가 3이라면 아까 공식에 의하면 null space의 차원이 7이다.
를 만족하는 특정 solution(particular solution)이 있다고 가정하자.
우리는 null space가 존재한다는 걸 알고 있기 때문에
라는 것도 알고 있다.
이때 역시 쉽게 납득할 수 있다.
이때 Null space의 원소는 무한이기 때문에 full row rank일때 해가 무한이다.
full rank (square matrix)일때 : 해가 오직 한 개 있다.
이 경우는 열벡터가 기저인 경우다 기저는 그 공간의 모든 벡터들을 표현할 수 있고 표현은 unique하므로 역행렬을 구할 수 있고 오직 해가 하나이다.
rank-deficient일때
이 경우는 full column rank와 비슷한데 단지 null space가 존재하기 때문에
해가 없거나 만약에 해가 존재한다면 그 해는 무한개이다. (full row rank 철학에 따라)
rank 계산
행렬의 계수는 가우스 소거법으로 기약행사다리꼴 해렬을 구하고 난 후, 모든 성분이 0인 행을 제외하고 나머지 행의갯수를 세어주면 된다. 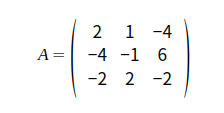
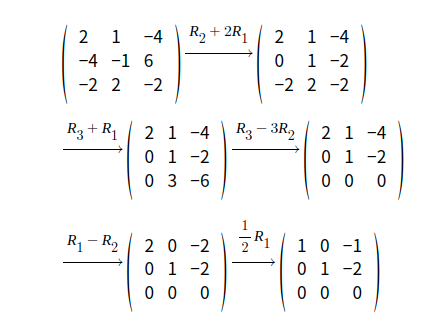
위의 A 행렬의 기약행사다리꼴의 3행의 모든 성분이 0이므로 계수는 2임을 확인할 수 있다.
그런데.... 잠깐!!! 왜 이렇게 구할 수 있는 거지? 무슨 근거로?
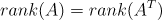
로 부터 행의 unique 벡터 갯수와 열의 unique 벡터 갯수가 같다는 사실을 알고 있다. 그래서 가우스 소거법은 unique한 행의 갯수로 rank를 계산한다.
그런데 저렇게 기약 사다리꼴은 왜 만들지?
2번째 행은 1열이 0이지? 즉 2행은 무슨짓을 해도 1행을 만들 수 없는 거다.
그런데 3번째 행은 다 0이지? 그 뜻은 3행은 1,2행벡터의선형결합으로 만들 수 있다는 것이다.
즉 저건 unique vector가 있는지 없는지 확인하기 위해서 저런 과정을 하는 것이다.

글 잘 읽었습니다.
중간에 투명배경에 수식을 쓰신 게 있는데, 다크모드에서 안보이네요.