📊 NBA TS% 분석 프로젝트 (2021–22 시즌, Detroit 중심)
1. 연구 질문
NBA 2021–22 시즌에서
상위팀(Top5, 플레이오프권)과
하위팀(Others, 나머지 팀)의 평균 TS%에 차이가 있는가?
그리고 Detroit Pistons는 리그 전체 분포 속에서 어느 위치에 있는가?
히스토그램으로 TS%를 그리는 이유 = 정규성 확인 (normality check)
시각적 확인 (exploratory check)
히스토그램, Q-Q plot
목적: “분포 모양이 정규에 가까운지 감 잡기”
특징: 주관적 해석, 오류 누적 문제 없음
통계적 검정 (formal test)
Shapiro-Wilk 등
p-value 기반 → 귀무가설: “데이터는 정규분포를 따른다”
특징: 여러 변수/집단에 대해 반복하면 다중검정 오류 가능
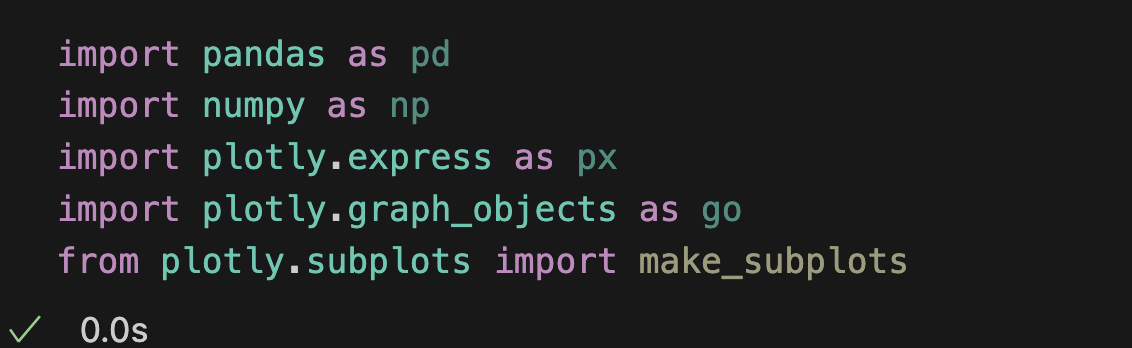
import pandas as pd
import numpy as np
import plotly.express as px
import plotly.graph_objects as go
from plotly.subplots import make_subplotsQ.2021-2022 시즌 디트로이트 팀 안에 선수들끼리 TS% 히스토그램 그려보는 건 표본수가 너무 작나???
- 표본 수 관점에서
히스토그램은 연속형 데이터를 구간(bin)으로 잘라서 빈도를 보는 것이라, 표본 수가 적으면 그래프가 울퉁불퉁하거나 의미 있는 분포가 안 보일 수 있음
NBA 한 시즌에 팀 선수 수(로스터)는 보통 15명 안팎이고, 실제 꾸준히 출장하는 건 8~10명 정도라서 히스토그램으로 보기엔 너무 적습니다.
→ 히스토그램은 보통 수십 개 이상 표본이 있어야 "분포"라는 걸 이야기하기 좋음
- 그럼 어떻게 해야 할까?
히스토그램 대신 막대그래프 (bar chart) → 선수별 TS%를 바로 비교하는 게 더 직관적임.
박스플롯(boxplot) → 만약 "팀 전체 TS% 분포"를 보고 싶다면 쓰기 괜찮지만, 샘플이 적어서 극적인 모양은 안 나올 수 있음.
리그 전체 선수 vs 디트로이트 선수 → 이때는 표본 수가 수백 명이라서 히스토그램으로도 충분히 분포 모양이 나와요. 그리고 그 안에 Detroit 선수들만 하이라이팅해주면 더 의미 있음.
- 결론
팀 내부 15명 정도로는 히스토그램 적합하지 않음.
대신:
선수별 bar chart로 TS% 비교
리그 전체 + Detroit overlay 히스토그램으로 팀이 어디쯤 분포하는지 확인
👉 내가 원하면 plotly 코드 예시로
(1) 디트로이트 선수들만 bar chart,
(2) NBA 전체 히스토그램 + Detroit 선수 강조
TS%
📌 요약: 왜 출전 시간 컷라인을 두는가?
극단값 제거
몇 분만 뛰고 TS% 100% 같은 선수 제거 필요.
신뢰성 확보
출전 시간이 많아야 TS%가 안정적으로 의미 있음.
검정 타당성
너무 적게 뛴 선수 포함 시 정규성 가정 깨질 수 있음 → t-검정 신뢰도 떨어짐.
📌 결론
컷라인(≥100분, ≥300분, ≥500분)을 두고 분석하는 게 맞다.
컷라인별 표본 수 확인 후, 충분한 샘플 확보되는 기준 선택.
이후 Detroit vs 리그 평균 비교 → t-검정 or 비모수 검정 진행.
🎯 프로젝트 목표
연구 질문: NBA 2021–22 시즌에서 상위팀(플레이오프권)과 하위팀(로터리권)의 평균 TS%에 차이가 있는가?
궁극적 목적:
TS% 차이가 실제로 존재한다면, 그 원인을 데이터로 분석하고
디트로이트 같은 하위팀이 어떤 부분을 개선해야 하는지 인사이트 도출
데이터 준비
경기 상세 데이터(games_details_regular.csv) 사용
선수별 출전 시간(TOTAL_MIN) 집계 → 100분/300분 이상 컷라인 적용
TS% 계산:
팀 단위 집계
선수별 TS% → 팀 평균 TS%로 변환 (출전 시간 가중 평균 가능)
각 팀의 시즌 TS% 산출
팀 분류
상위팀: 정규시즌 승률 상위 (예: 1~10위)
하위팀: 정규시즌 승률 하위 (예: 21~30위)
가설 검정
귀무가설(H₀): 상위팀과 하위팀의 평균 TS% 차이는 없다.
대립가설(H₁): 상위팀과 하위팀의 평균 TS% 차이가 있다.
방법: 독립표본 t-검정 (정규성 만족 시) / 비모수 검정 (정규성 불만족 시)
시각화
NBA 전체 선수 TS% 히스토그램 (DET 강조)
상위팀 vs 하위팀 박스플롯 / 바차트
컷라인별 TS% 분포 비교
해석
상위팀과 하위팀 간 TS% 평균 차이 유무
차이가 있다면 → 어느 지표(2P, 3P, FT, eFG%)에서 벌어지는지 추가 분석
디트로이트 팀에 대한 구체적 시사점 도출
t-검정: 디트로이트와 상위팀의 TS% 평균 차이가 있는가?
카이제곱 검정:
디트로이트의 승/패 결과가 리그 평균 승/패 분포와 다른가?
포지션별(가드/포워드/센터) 턴오버 발생 빈도가 팀 간에 독립적인가?
👉 정리하면:
평균·효율 → t-검정
빈도·비율 → 카이제곱
컷라인 선별!!
📌 컷라인 선정 원칙
1️⃣ 데이터 안정성 (표본 신뢰성)
출전 시간이 짧으면 TS%, FG%, 3P% 같은 효율 지표가 극단적으로 튀어요.
→ 최소 100분 이상: 의미 없는 샘플 제거 (기본 컷).
→ 300분 이상: 어느 정도 경기 샘플 확보 (보통 벤치 자원도 포함).
→ 500분 이상: 주전급 이상만 남음 (데이터 안정성 ↑).
2️⃣ 분석 목적
팀 전체 효율성을 보려는 목적이라면 → 100분 이상으로 넓게 잡아 팀 전체 그림 파악.
주요 로테이션 선수 위주 분석이라면 → 300분~500분 이상으로 좁게 잡는 게 적합.
3️⃣ 표본 수와 검정력 (Statistical Power)
컷라인을 높이면 신뢰성은 좋아지지만 → 표본 수가 줄어서 검정력이 약해짐.
컷라인을 낮추면 표본 수는 많아지지만 → 데이터가 시끄러워져서 정규성 가정이 흔들림.
💡 그래서 “적절히 균형”을 잡는 게 핵심
📊 실무적 접근
컷라인별 표본 수 확인
≥100, ≥300, ≥500, ≥1000 분 기준으로 선수 수를 확인.
시각화
컷라인별 TS% 히스토그램이나 박스플롯을 그려보고, 분포가 얼마나 안정되는지 비교.
최종 선택
Detroit vs 리그 전체 비교라면 표본 수를 충분히 확보해야 하므로 → 보통 300분 컷을 많이 씀.
“정말 코어 선수만 보고 싶다”면 500분 이상 컷도 가능.
✅ 정리:
100분 이상: 기본 노이즈 제거용 컷
300분 이상: 표본 수와 안정성 균형
500분 이상: 주전급 이상, 정밀 비교
TS% 비교하기 전 표본수 확보 시즌 전체 출전 시간 중에서 300분이상 뛴애들의 표본수를 가지고 비교하려고 하는데 그거에 대한 연구가 되었는지 확인
네, TS%를 비교하기 위해 일정 최소 출전 시간을 기준으로 선수를 필터링하는 방식에 대한 연구 및 분석은 활발하게 이루어지고 있습니다. 300분이라는 구체적인 수치보다는 더 일반적인 "최소 플레이 시간" 또는 "최소 게임 수"를 설정하여 표본의 신뢰성을 확보하려는 시도가 많습니다.
관련 연구 및 분석 내용
표본 크기와 통계적 유의성: 농구 통계 분석에서는 특정 지표의 신뢰도를 높이기 위해 최소한의 플레이 시간 또는 게임 출전 횟수를 설정하는 것이 일반적입니다.
NBA 공식 기준: NBA는 특정 통계 부문 리더 자격을 얻기 위한 최소 게임 수 또는 필드골/자유투 시도 횟수 등의 기준을 명시하고 있습니다. 예를 들어, 리더 보드에 이름을 올리려면 팀 경기 수의 70%(82경기 시즌 기준 58경기)를 플레이해야 합니다. TS% 리더에는 특정 최소 득점(Total Points)이 요구되지는 않지만, 필드 골 % 리더는 300개의 필드 골 성공, 자유투 % 리더는 125개의 자유투 성공이 요구됩니다. 이런 기준들은 효율성 지표의 유의미한 비교를 위한 최소 표본 크기를 간접적으로 나타냅니다.
300분 기준의 합리성:
총 출전 시간 300분은 한 시즌 동안 약 8-9경기에서 35분씩 출전하는 것과 유사한 시간입니다.
이 정도의 플레이 시간은 선수가 다양한 상황에서 충분한 슈팅 시도를 가졌을 가능성이 높습니다.
일반적으로 NBA에서 중요한 로테이션 멤버나 핵심 선수는 한 시즌에 30분 이상 출전하는 경우가 많습니다.
짧은 시간 동안의 플레이는 운이나 특정한 상황에 의해 과대평가될 수 있는 반면, 300분 이상의 표본은 선수의 실제적인 효율성을 더 잘 반영할 수 있습니다.
플레이 시간의 영향: 플레이 시간은 농구 선수의 경기 관련 통계에 강한 영향을 미치며, 일반적으로 더 많은 시간을 뛸수록 더 나은 경기력을 보이고 실수가 적어집니다. 또한, 플레이 시간은 팀의 질과 선수의 포지션에도 영향을 받습니다.
초고효율성 예외: NBAstuffer에 따르면 만약 한 선수가 교체 투입되어 3점슛만 성공시키고 나머지 경기에서 플레이하지 않는다면, 그의 TS%는 150%에 달할 수도 있다고 설명합니다. 이런 극단적인 상황을 배제하기 위해 최소 출전 시간 기준을 두는 것은 합리적입니다.
결론
300분이라는 구체적인 수치가 특정 연구에서 "최적의" 표본 크기로 제시되었는지는 명확하지 않지만, TS%와 같은 효율성 지표를 비교할 때 최소 출전 시간을 기준으로 삼는 것은 통계적 신뢰성을 확보하기 위한 합리적이고 널리 사용되는 방법입니다. 짧은 플레이 시간은 통계적 변동성이 크기 때문에, 일정 수준 이상의 출전 시간을 보장하는 것은 선수의 진정한 효율성을 파악하는 데 도움이 됩니다.
https://share.google/N3SSrC6SKzrh7rv8W
https://en.wikipedia.org/wiki/True_shooting_percentage
https://share.google/KJKRACAp9732rHTRC
https://share.google/bdWfwKSd3YT0Uzs1S
📚 출전 시간 컷라인 사례 / 관련 연구 사례
직접적으로 “NBA 분석에서 300분 이상 출전”처럼 명시한 연구는 드물지만, 스포츠·운동과학 / 경기 분석 분야에서는 유사한 기준이 자주 등장해요:
어떤 농구 장비 추적 연구에서는 “한 경기 최소 20분 이상 뛴 선수만 분석 대상에 포함”하는 기준을 쓴 경우 있음 (운동량 분석 연구)
MDPI
여러 경기·운동 분석 문헌에서는 “출전 시간이 rất 적은 선수는 분석 대상에서 제외”하는 것이 일반적 관행
또 축구나 럭비 쪽에서도 “일정 경기수 이상 출전” 또는 “일정 시간 이상 활동” 기준을 두는 연구 많음
즉, 컷라인은 엄밀한 법칙이기보단 도메인 지식 + 데이터 분포 + 분석 목적을 고려해 결정하는 게 보통
컷라인 세우기
📌 해석
100분 이상
거의 모든 DET 선수 포함 (13명).
하지만 여전히 샘플 불안정한 선수 있을 수 있음.
300분 이상
전체 311명, DET도 여전히 13명 → 즉, DET는 주요 로테이션 선수들이 대부분 300분 이상 뛰었음.
안정성과 표본 수 균형 잡힘.
500분 이상
DET는 6명으로 줄어듦 → 주전급만 남음.
표본 적어서 검정력이 떨어질 수 있음.
1000분 이상
DET는 1명밖에 안 남음 → 사실상 분석 불가.
✅ 결론 (추천 컷라인)
300분 이상: DET 표본 13명, 리그 표본 311명 → 비교에 충분.
500분 이상: “주전급만 분석”이라는 스토리를 강조할 때 사용 가능.
1000분 이상: 표본 너무 작아서 분석 불가.
👉 그래서 주 분석은 ≥300분 기준으로 하고,
보조 분석으로 “주전만 보겠다”면 ≥500분 기준 추가하면 좋을 것 같음???
팀 전체 평균 TS% 비교가 먼저,
그다음에 DET 300분 이상 선수 개별 분석으로 내려가면 되지 않을까?.
선수 이름만 보면 누가 주전/로테이션인지 알 수 있으니 충분히 의미 있는 해석 가능
그럼 선수마다 position 을 value_counts 쓰면 누가 주전인지도 알수 있지 않을까?
Step 1: Top5 vs Others → 두 그룹의 전반적인 차이 확인 (검정 가능)
Step 2: Detroit 평균 위치를 박스플롯/히스토그램 위에 표시 → 리그 내 위치 설명
Step 3: “Detroit는 상위 5팀 평균보다 얼마나 낮은가?” → 단순 차이 수치로 제시
📌 왜 “나머지 팀(=Others)” 그룹이 필요할까?
비교 가능한 두 집단 만들기
귀무가설(H₀): Top5 팀과 나머지 팀의 TS% 평균은 차이가 없다
대립가설(H₁): Top5 팀과 나머지 팀의 TS% 평균은 차이가 있다
→ 따라서 “Top5 vs Others”라는 두 그룹이 있어야 t-검정 같은 비교가 가능해요.
DET 단독 비교의 한계
DET만 떼어놓으면 1개의 데이터포인트 → “집단”이라 보기 어려움.
검정 대신 단순 비교(DET 평균 vs Top5 평균 차이)만 가능.
그래서 DET는 Others 그룹 안에 속한 팀 중 하나로 두고, 위치를 별도로 강조하는 게 더 타당.
시각화/설득력
박스플롯: Top5 vs Others 두 박스로 분포를 보여주고, DET를 빨간 점으로 찍어 강조 → 훨씬 설득력 있는 그림.
“DET는 리그 평균 중에서도 하위권에 위치한다”라는 메시지가 명확해짐.
같은 테이블 안에서 그룹 라벨을 붙여서 비교하는 게 정석이에요.
Q.일단 같은 테이블에서 비교하는 건가?서로 다른 데이터프레임으로 비교하는게 아니라??
📌 이유
하나의 DataFrame에 담아야
시각화 (박스플롯, 히스토그램)에서 x="Group", y="TS%" 이렇게 쉽게 표현 가능
통계 검정할 때도 df[df['Group']=='Top5']['TS%'] vs df[df['Group']=='Others']['TS%'] 형태로 뽑을 수 있음
다른 DataFrame으로 따로 만들면
나중에 시각화나 검정할 때 다시 합쳐야 해서 오히려 번거로움
# 팀별 TS% 평균
team_ts = df1.groupby('TEAM', as_index=False)['TS%'].mean()
# Top5 팀 리스트
top5_teams = team_ts.sort_values('TS%', ascending=False).head(5)['TEAM'].tolist()
# 같은 테이블 안에 그룹 라벨 추가
team_ts['Group'] = team_ts['TEAM'].apply(lambda x: 'Top5' if x in top5_teams else 'Others')
# 검정 시 이렇게 사용
top5_values = team_ts[team_ts['Group']=='Top5']['TS%']
others_values = team_ts[team_ts['Group']=='Others']['TS%']
📦 Trace(트레이스)란?
Plotly에서 Trace = 그래프에 그려지는 하나의 데이터 집합
예를 들어:
막대그래프 한 묶음 = 1개의 trace
산점도 점 모음 = 1개의 trace
선 그래프 선 하나 = 1개의 trace
즉, Trace는 그래프에 올라가는 “도형/데이터 레이어” 한 덩어리라고 보면 됩니다.
** 📌 add_trace() 함수
이미 만들어진 Figure(캔버스)에 새로운 Trace를 올리는 함수예요.
예시 1: Scatter 점 하나 추가
fig = go.Figure() # 빈 그래프 캔버스
fig.add_trace(go.Scatter(x=[1,2,3], y=[4,5,6], mode="lines"))
fig.show()
→ 빈 캔버스에 선 그래프(Trace 하나) 추가
예시 2: 기존 그래프에 강조점 찍기
fig = px.box(df, x="Group", y="TS%") # 박스플롯 (Trace 1개 생성)
fig.add_trace(go.Scatter(x=["Others"], y=[0.52],
mode="markers+text",
text=["Detroit"],
marker=dict(color="red", size=12)))
fig.show()
→ 원래 박스플롯(Trace 1개)에, 빨간 점(Trace 2개째)을 추가
✅ 한마디로
add_trace() = “그래프에 새로운 레이어를 올리는 함수”
여기서 go.Scatter(...)는 그 레이어(Trace)를 만드는 코드
즉, fig.add_trace(go.Scatter(...)) =
“지금 그림(fig)에 산점도(점 하나)를 하나 더 올려라”
📖 옵션별 설명
1. mode="markers+text"
mode는 그래프에 뭘 그릴지 정하는 것
"markers" → 점(●) 표시
"text" → 글자 표시
"lines" → 선 표시
"markers+text" → 점 + 글자를 같이 그림
👉 여기서는 Detroit 평균을 빨간 다이아몬드 + 글자로 동시에 보여주려는 것
-
text=["Detroit"]
점 옆에 표시할 글자
"Detroit"라는 텍스트가 점 위에 같이 표시됨
리스트로 준 이유는, 점이 여러 개일 수도 있으니까 각각 매칭되도록 설계됨 -
textposition="top center"
글자가 점에 비해 어디 위치에 올지 정함
"top center" → 점 위쪽 가운데에 글자 표시
다른 예시: "bottom right", "middle left" 등
- marker=dict(...)
점의 모양(마커)을 설정하는 옵션
세부 속성:
color="red" → 점 색깔 빨강
size=12 → 점 크기 12
symbol="diamond" → 점 모양을 다이아몬드로
Plotly에는 "circle", "square", "triangle-up" 같은 심볼도 많아요.
박스플롯을 쓰는 이유
이런 특징 때문에 박스플롯은 연속형 변수의 분포을 비교하고 요약하기에 매우 효율적인 시각화 방식
예를 들어 “상위팀 vs 하위팀 TS% 분포 차이” 혹은 “포지션별 TS% 분포 비교” 같은 경우 박스플롯이 직관적이고 유용
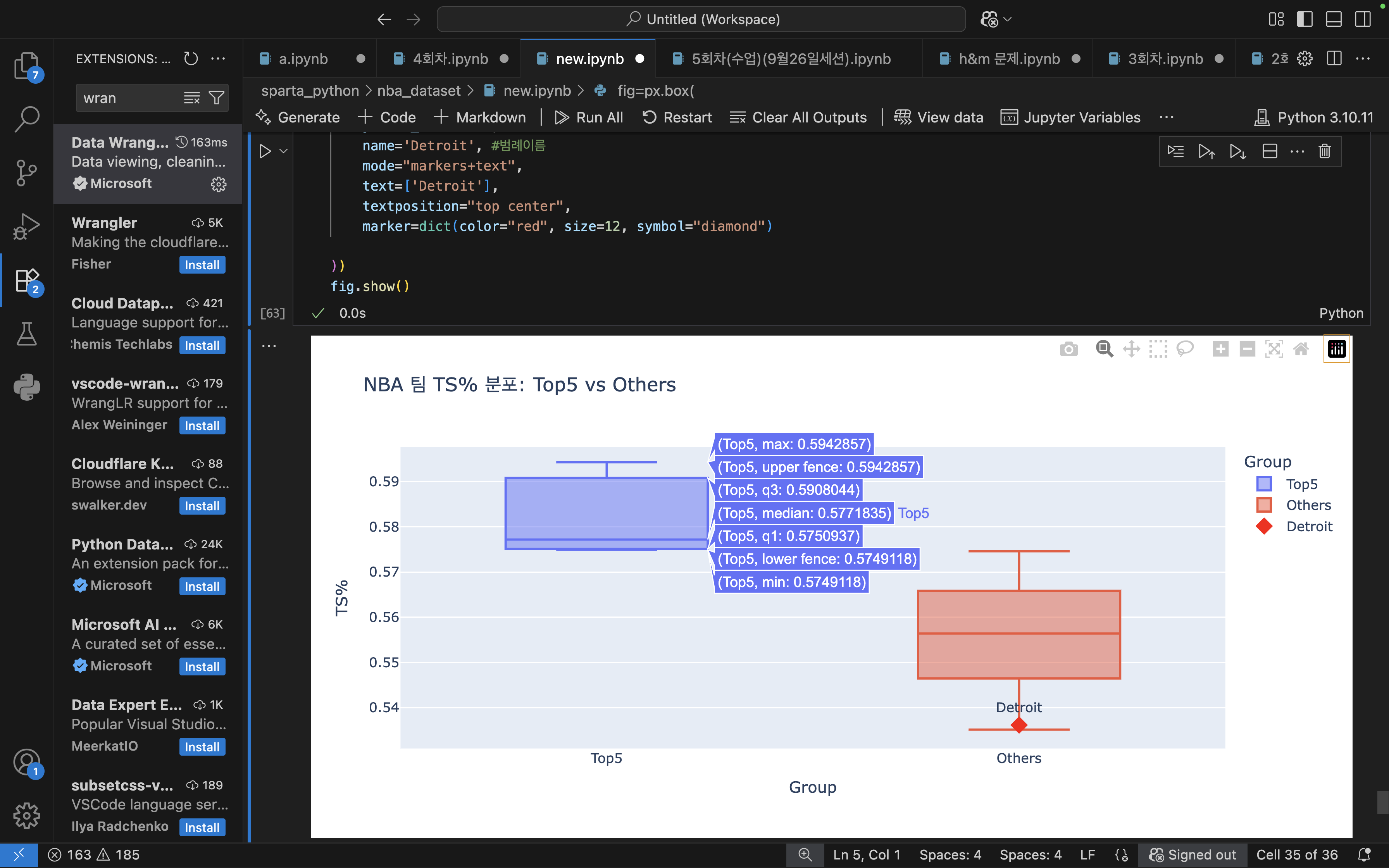
📊 그래프 1 (첫 번째 박스플롯)
Top5 (파란색)
중간값(median) ≈ 0.577
범위가 좁음 → 대부분 팀들이 효율적으로 슛 성공률이 비슷하게 높음
Others (빨간색)
중간값(median) ≈ 0.556
범위가 넓음 → 팀마다 편차가 큼 (좋은 팀도 있지만, 낮은 팀도 많음)
Detroit (빨간 다이아몬드)
Others 그룹 안에서도 가장 아래쪽에 위치
즉, 다른 하위팀들과 비교해도 효율이 낮은 편
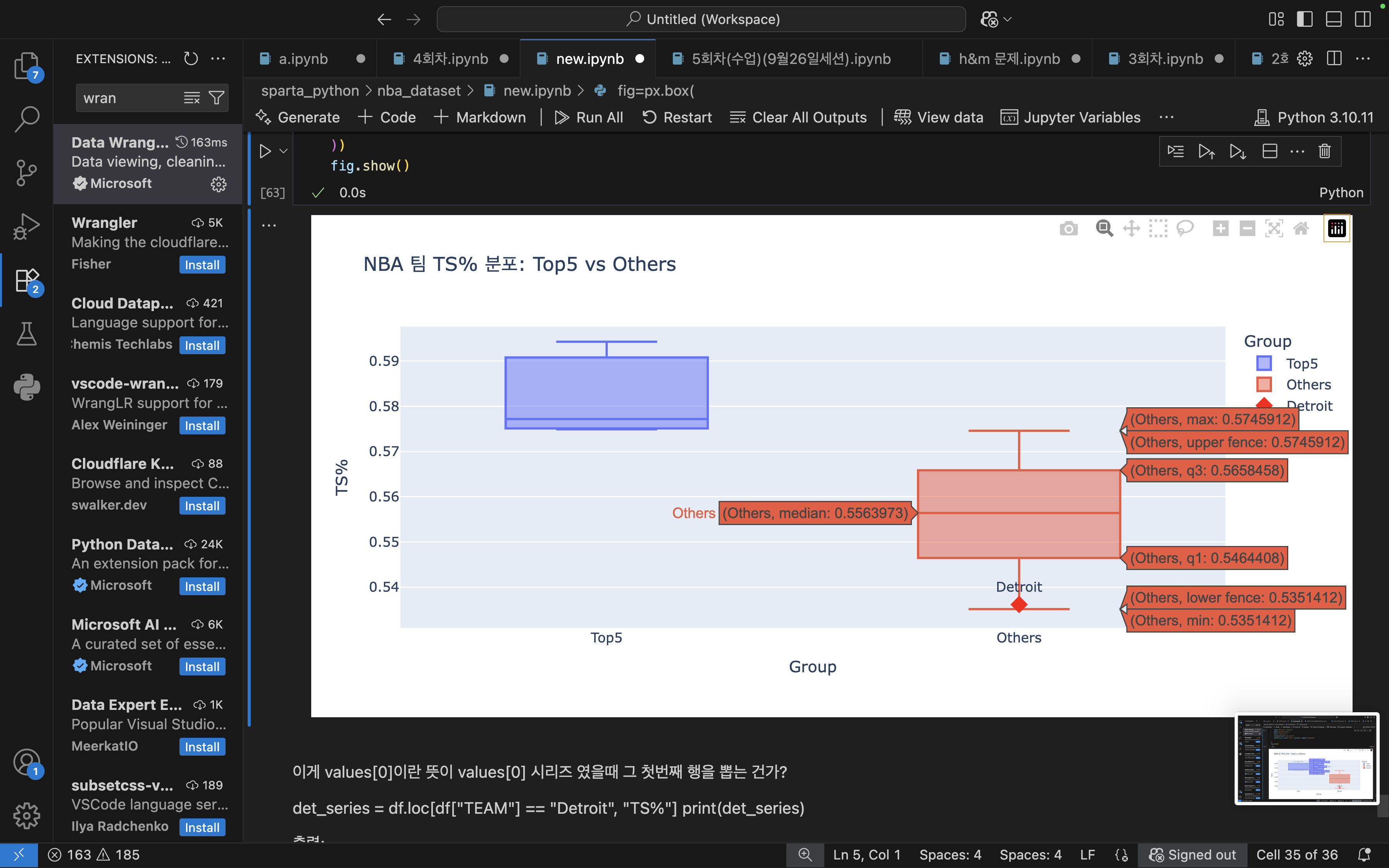
📊 그래프 2 (Tooltip 포함)
박스플롯의 구체적인 수치 확인 가능
Top5 팀들의 Q1, Q3, min, max 값 → 0.574 ~ 0.594 구간에 몰려있음
Others 팀들의 Q1, Q3 값 → 0.546 ~ 0.566 로 더 낮고 퍼짐
Detroit = 약 0.535 → Others의 하위 25% (Q1)보다도 밑에 있음
📌 두 그래프 통해 알 수 있는 것
상위팀 vs 하위팀 차이
Top5 팀은 TS%가 높고 안정적 (효율 + 일관성)
Others 팀은 낮고 불안정 (팀별 편차 큼)
Detroit의 상대적 위치
리그 전체 평균보다 낮음
Others 그룹 안에서도 최하위권
→ 공격 효율 개선이 시급하다는 근거가 됨
데이터 신뢰성
단순 평균 비교가 아니라 분포(박스플롯)로 비교했기 때문에
"Detroit는 운이 나빠서 낮은 게 아니라, 구조적으로 낮다"는 걸 강조할 수 있음
✅ 요약하면:
Top5는 효율적이고 안정적
Detroit는 Others 그룹 중에서도 최악 수준
→ Detroit가 리그에서 떨어지는 이유가 슛 효율(공격 효율)임을 시각적으로 증명

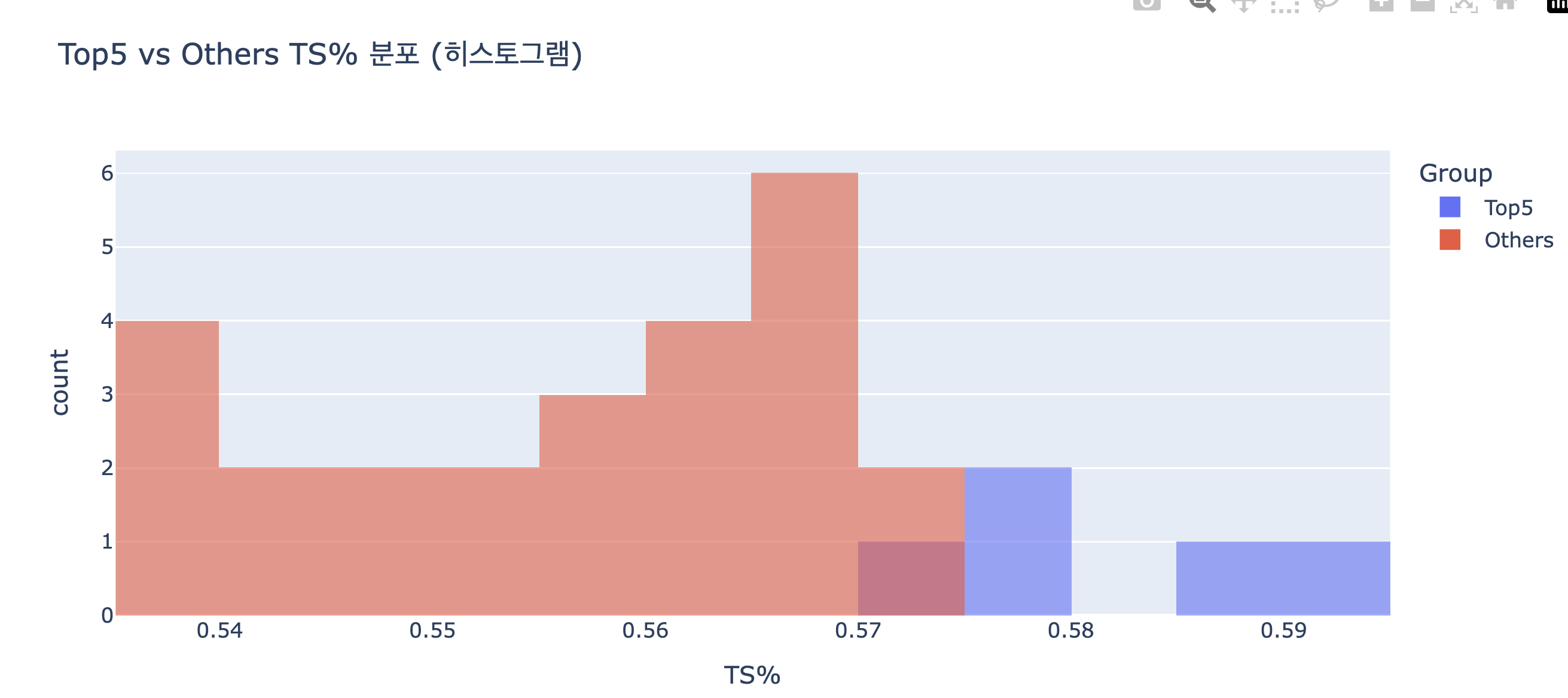
📊 해석 포인트
Top5 (파란색) 분포
TS%가 전반적으로 0.575 ~ 0.59 근처에 몰려 있음
분포가 좁음 → 상위권 팀들이 효율적으로 슛을 꾸준히 잘 넣고 있다는 의미
Others (빨간색) 분포
TS%가 0.54 ~ 0.57 근처에 넓게 퍼져 있음
일부는 괜찮지만, 다수는 낮은 구간에 위치 → 팀마다 편차가 큼
겹치는 부분
약간 겹치는 부분(0.57 근처)이 있지만,
전체적으로는 Top5가 더 오른쪽(효율 ↑), Others가 왼쪽(효율 ↓)
📌 결론
히스토그램만 봐도 Top5 팀은 TS%가 높고 안정적
Others 팀은 낮고 변동이 크다
Detroit는 “Others 그룹 안에서 특히 낮음”을 박스플롯에서 이미 확인했으니,
히스토그램 + 박스플롯 조합으로 설명하면 신뢰도가 훨씬 높아질 것
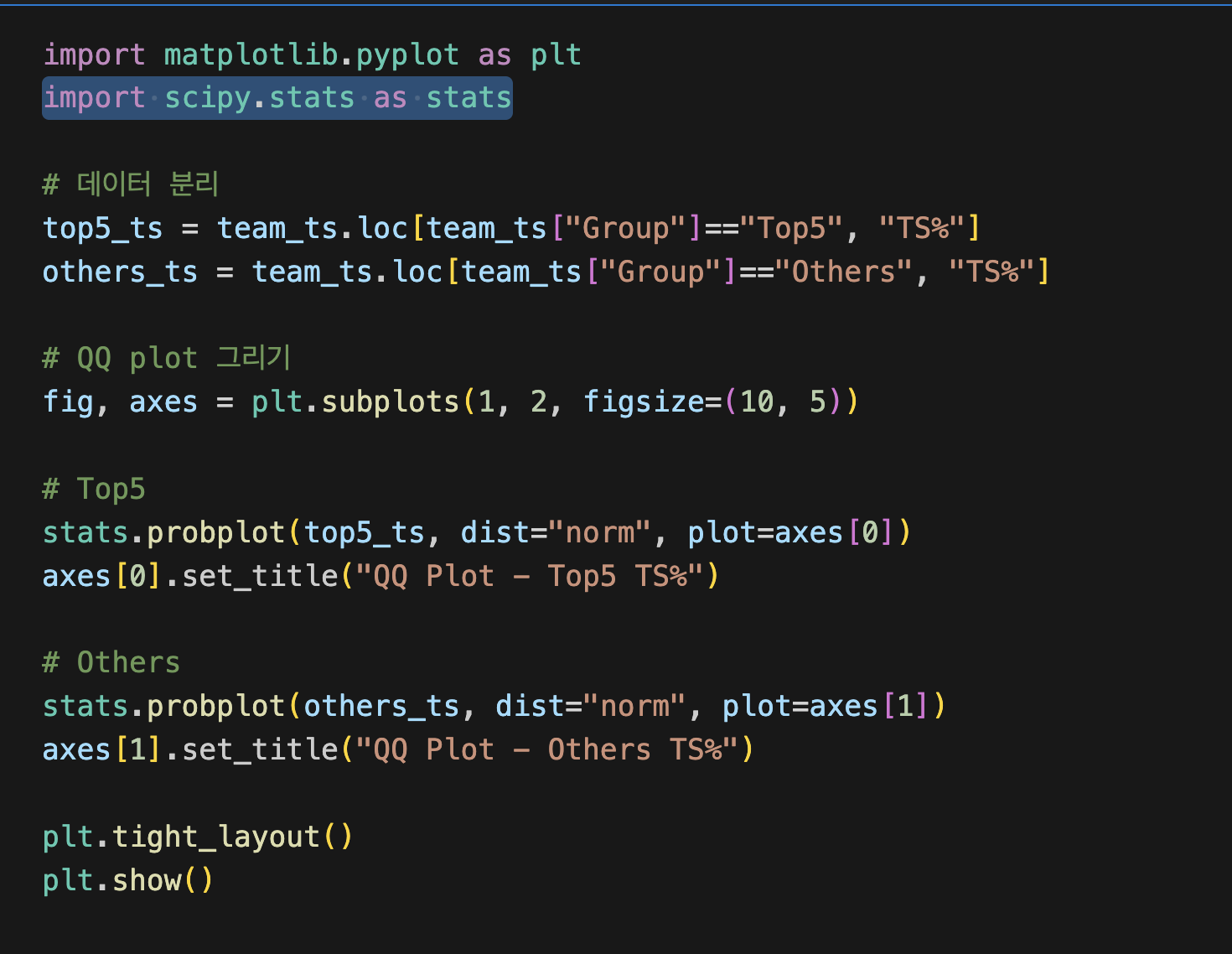
fig,axes=plt.subplots(1,2, figsize=(10,5)
1행 2열짜리 플롯(그래프 2개)을 한 Figure 안에 생성
fig = 전체 그림 틀, axes = 2개의 축 객체 (왼쪽, 오른쪽)
figsize=(10, 5) → 그림 크기 가로 10, 세로 5
Top5
stats.probplot(top5_ts, dist="norm", plot=axes[0])
axes[0].set_title("QQ Plot - Top5 TS%")
stats.probplot() → 데이터와 정규분포 분위(quantile)를 비교하는 QQ plot 생성
dist="norm" → 비교 기준이 정규분포
plot=axes[0] → 첫 번째 subplot(왼쪽)에 그리기
set_title() → 그래프 제목을 "QQ Plot - Top5 TS%"로 지정
plt.tight_layout()
- 시각적 확인 (Boxplot)
Top5 분포: 평균 높음, 분산 좁음 → 효율이 높고 안정적
Others 분포: 평균 낮음, 분산 넓음 → 효율이 낮고 편차 큼
추측: 분산이 다를 것 같음 → Welch’s t-test가 필요할 수 있다.
- 정규성 검정 (Shapiro-Wilk + QQ plot)
Top5: p=0.105 (>0.05) → 정규성 기각 못 함
Others: p=0.091 (>0.05) → 정규성 기각 못 함
결론: 두 그룹 모두 정규성을 따른다고 가정 가능 ✅
- 등분산성 검정 (Levene test)
귀무가설(H₀): 두 그룹의 분산은 같다.
결과(p값에 따라):
p > 0.05 → Student’s t-test (등분산 가정)
p ≤ 0.05 → Welch’s t-test (등분산 가정 없음)
- t-검정 실행
Student’s t-test (equal_var=True)
Welch’s t-test (equal_var=False)
결론: Levene test 결과에 따라 올바른 t-test 선택
서브플롯들 간격을 자동으로 맞춰서 글자/그래프가 겹치지 않게 함
t-검정은 전제가 있음
각 그룹(Top5, Others)의 데이터가 정규분포를 따른다 → 이게 기본 가정
그래서 두 그룹 각각 따로 정규성 검정을 해줘야 함
📌 왜 따로 해야 할까?
만약 Top5는 정규성을 만족하지만, Others는 깨진다면?
→ t-검정은 부적절 → 대신 비모수 검정 (Mann-Whitney U test) 사용해야 함
만약 둘 다 정규성을 만족한다면?
→ t-검정 진행 가능 (추가로 등분산성도 확인하면 더 좋음, Levene test 같은 걸로).

등분산성 검정
📌 Levene Test의 귀무가설 (H₀)
H₀: 두 집단(Top5, Others)의 분산은 같다.
H₁: 두 집단의 분산은 다르다.
📊 결과 해석

p-value = 0.296 (> 0.05)
👉 귀무가설을 기각할 수 없음
👉 즉, 두 그룹의 분산은 통계적으로 차이가 없다 = 등분산성 가정 충족
t_test t검정
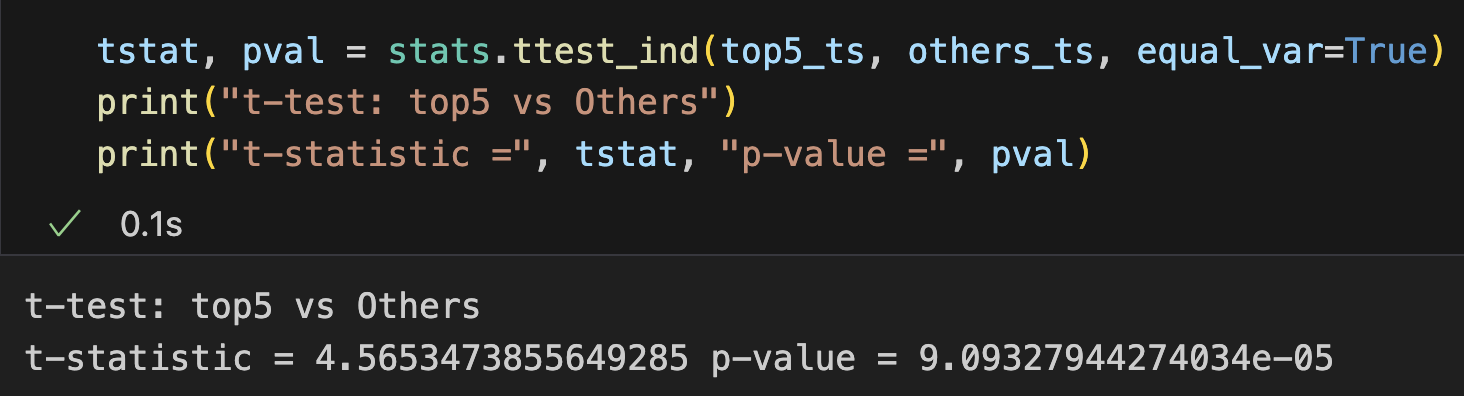
✅ 결과 요약
t-statistic = 4.565
p-value = 9.09e-05 (≈ 0.00009)
유의수준(α) = 0.05 기준
📌 해석
귀무가설(H₀): Top5 팀과 Others 팀의 평균 TS%는 같다.
대립가설(H₁): 두 그룹의 평균 TS%는 다르다.
👉 p-value ≈ 0.00009 < 0.05 이므로 귀무가설을 기각합니다.
즉, Top5와 Others는 평균 TS%에서 통계적으로 유의한 차이가 있다고 결론 내릴 수 있습니다.
📊 추가 해석 (NBA 데이터 맥락)
Top5 팀의 평균 TS%는 Others 팀보다 유의미하게 높다.
단순히 박스플롯이나 히스토그램으로 본 시각적 차이가 통계적으로도 입증된 셈.
따라서 "슛 효율(TS%)이 높은 팀일수록 리그 상위권에 위치한다"라는 주장을 데이터로 뒷받침할 수 있음 ✅.
Q. 만약에 가설 검정을 안했더라면 ??
📌 만약 검정을 안 하면 생기는 문제
1. 눈대중 판단의 오류
박스플롯이나 히스토그램만 보고 “차이가 있어 보인다”라고 결론내리면,
실제로는 우연(랜덤 샘플링 오차) 때문에 그렇게 보였을 수도 있습니다.
→ 시각적 차이가 통계적으로 유의한 차이인지는 확인 불가.
- 재현성 부족
“Top5가 더 높아 보인다”라는 해석은
다른 표본을 뽑거나 다른 시즌 데이터를 쓰면 달라질 수 있습니다.
→ 검정을 통해 우연이 아닐 확률(p-value)을 제시해야 다른 분석가/코치/구단주에게 설득력이 생김.
- 오판 위험 (Type I / II Error)
검정을 안 하면 1종 오류(차이가 없는데 있다고 믿음)나
2종 오류(차이가 있는데 없다고 믿음) 위험이 커져요.
검정은 이런 오류 확률을 수치(유의수준 α)로 관리할 수 있게 해줍니다.
- 의사결정의 근거 부족
스포츠 데이터 분석에서 “Top5는 Others보다 효율이 높다 → 슛 선택/훈련 전략 강화 필요” 같은 인사이트를 주려면,
그 차이가 신뢰할 만한 수치여야 합니다.
→ 그냥 그래프만 보고 말하면, 코치나 구단주는 “이건 네 눈에만 그렇게 보이는 거 아냐?”라고 반문할 수 있음.
✅ 정리
검정을 안 하면,
보이는 차이가 우연인지 진짜 차이인지 모른다
객관적 근거 없이 주관적 판단에 의존하게 된다
실제 전략/투자 결정에서 신뢰도가 떨어진다따라서 통계적 검정은 “차이가 우연이 아님을 수치로 보장하는 과정”이라고 할 수 있음
