[코딩테스트] 소수 찾기

문제 설명

1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요.

소수는 1과 자기 자신으로만 나누어지는 수를 의미합니다.
(1은 소수가 아닙니다.)

제한 조건
n은 2이상 1000000이하의 자연수입니다.

입출력 예

n	result
10	4
5	3

• 입출력 예 #1
  1부터 10 사이의 소수는 [2,3,5,7] 4개가 존재하므로 4를 반환
• 입출력 예 #2
  1부터 5 사이의 소수는 [2,3,5] 3개가 존재하므로 3를 반환

---

문제 풀이

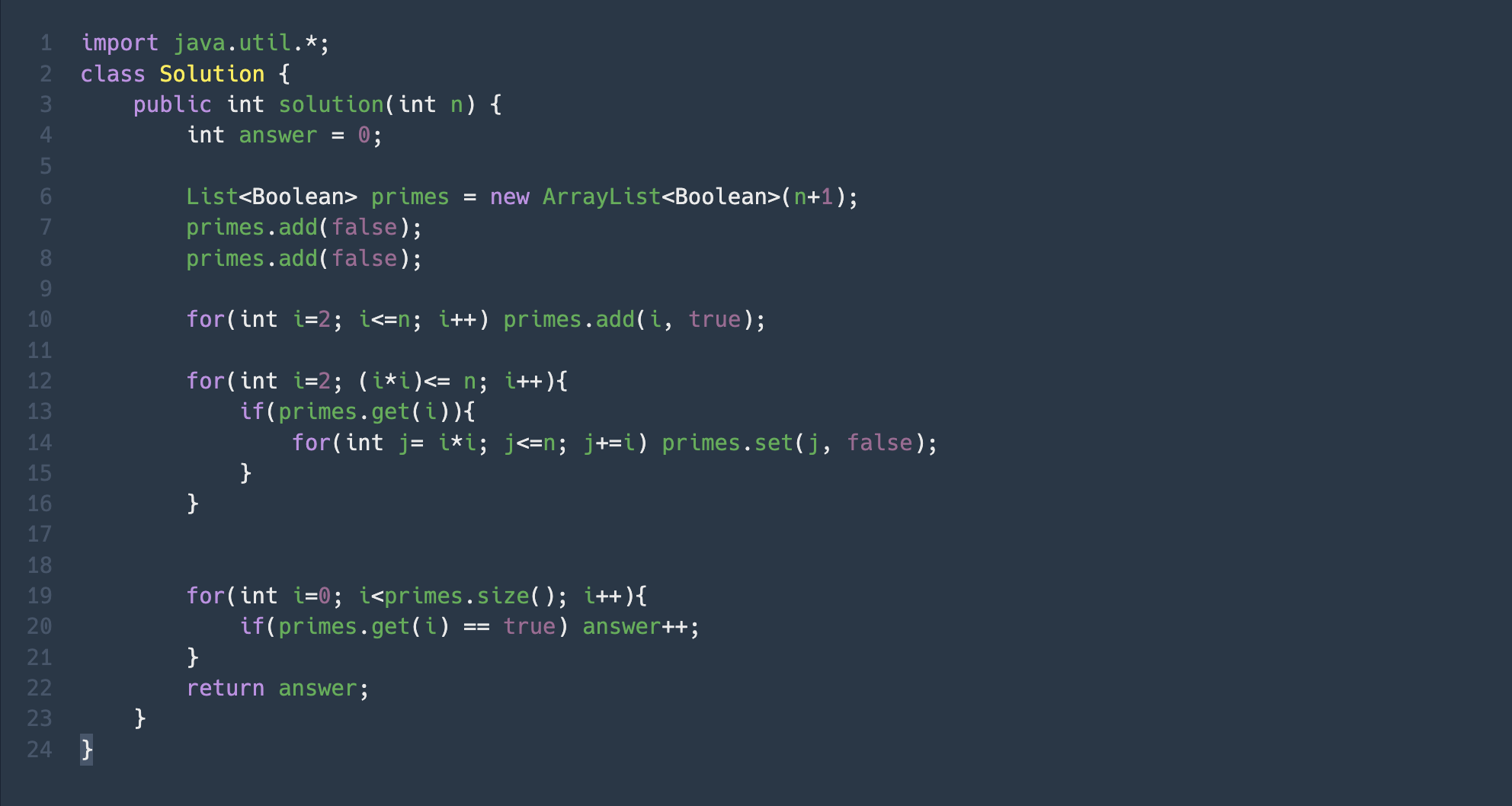
import java.util.*;
class Solution {
    public int solution(int n) {
        int answer = 0;
     
        List<Boolean> primes = new ArrayList<Boolean>(n+1);
        primes.add(false);
        primes.add(false);
      
        for(int i=2; i<=n; i++) primes.add(i, true);
     
        for(int i=2; (i*i)<= n; i++){
            if(primes.get(i)){
                for(int j= i*i; j<=n; j+=i) primes.set(j, false);
            }
        }
             
        for(int i=0; i<primes.size(); i++){
            if(primes.get(i) == true) answer++;
        }
        return answer;
    }
}

---

정답 찾아가는 과정

class Solution {
    public int solution(int n) {
        int answer = 0;
       
        for(int i=2; i<n+1; i++) {

            int cnt = 0;
            for(int j=1;j<i+1;j++) {
                if(i%j == 0)cnt++; 
            }
            if (cnt ==2 ) answer+=1;
        }
        return answer;
    }
}

처음엔 이렇게 풀었을 때 테스트를 통과했다. 그래서 채점을 했는데 띠용 이게 무슨 일 효율성 테스트를 통과하지 못했다.

%의 연산 시간이 길어 효율성 테스트를 통과하지 못한 것이라 판단했다. 그렇다면 그럼 어떻게 해결해야 하는가에 대해 고민했는데 검색을 해보니에라토스테네스의 체 알고리즘을 사용하면 된다고 한다.

에라토스테네스의 체

1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사2. 각형으로 두른 수들이 여기에 해당한다.
2. 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
3. 자기 자신을 제외한 2의 배수를 모두 지운다.
4. 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
5. 자기 자신을 제외한 3의 배수를 모두 지운다.
6. 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
7. 자기 자신을 제외한 5의 배수를 모두 지운다.
8. 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
9. 자기 자신을 제외한 7의 배수를 모두 지운다.
10. 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
    

해당 알고리즘을 사용하여 문제를 해결할 수 있었다.
그리고 내가 처음 시도한 문제풀이도 반복문 안에 j가 i만큼 돌 필요 없이 Math.sqrt(i)만큼만 돌면 효율성 문제를 해결할 수 있다고 하는 내용을 봤는데 시도 해봤더니 오류가 있어서 좀 더 연구를 해봐야 할 것 같다.

출처: https://ko.wikipedia.org/wiki/%EC%97%90%EB%9D%BC%ED%86%A0%EC%8A%A4%ED%85%8C%EB%84%A4%EC%8A%A4%EC%9D%98_%EC%B2%B4