🚀 3D Gaussian Splatting을 활용한 실시간 Radiance Field 렌더링 ; 3D Gaussian Splatting for Real-Time Radiance Field Rendering(SIGGRAPH 2023) 논문 리뷰

류동훈·2025년 1월 31일

arxiv: https://arxiv.org/abs/2308.04079
Github: https://github.com/graphdeco-inria/gaussian-splatting
Homepage: https://repo-sam.inria.fr/fungraph/3d-gaussian-splatting/

1. Introduction

최근 몇 년간 NeRF(Neural Radiance Fields) 기반 기법이 새로운 시점 합성(novel-view synthesis) 분야에서 혁신을 이루었으나, 높은 연산 비용으로 인해 실시간 렌더링에는 한계가 있었다. 3D Gaussian Splatting for Real-Time Radiance Field Rendering 논문은 이러한 문제를 해결하기 위해 3D 가우시안 스플래팅(3D Gaussian Splatting)을 도입하여 기존 방법보다 빠르면서도 높은 품질을 유지하는 렌더링을 가능하게 한다. 본 리뷰에서는 논문의 핵심 개념, 성과, 장점, 그리고 한계를 분석하고, 논문에 포함된 주요 수식과 최적화 과정(Optimization)을 상세히 설명한다.

3D Gaussian Splatting

3D Gaussian Splatting 네이밍에 대한 의미를 생각해보자면, Splat이라는 단어의 의미가 물기를 머금은 뭔가가 부딪치는 모습에 대한 의성어로써, 3D Gaussian이 흩뿌려진다라고 생각하면 좋을 것 같습니다.

3D Gaussian의 개념에 대해서 간단하게 설명해 드리겠습니다.

우선 Gaussian에 대해 알아보자.

가우시안은 확률에서 정규분포의 확률 밀도 함수(PDF)를 나타낼 때 주로 사용되는 함수이다. 평균, 분산, 표준편차만으로 정의될 수 있다는 것이 특징이다.

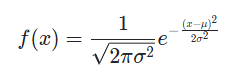
$μ$ : 평균
$σ^2$ : 분산 (표준편차 σ의 제곱)
$x$ : 확률 변수

가우시안의 대표적인 특징은 평균을 중심으로 대칭적으로 분포하며, 분산이 클수록 데이터가 더 넓게 퍼지며 분포가 낮아진다.

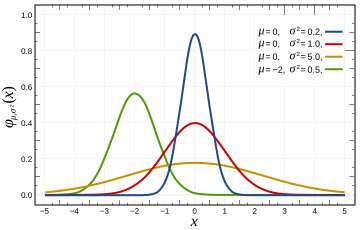
이 Gaussian을 바탕으로 3차원에서의 3D Gaussian이 파생되는데,

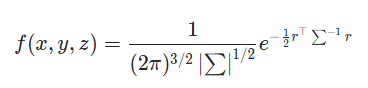
r = : 평균(μ)에서의 거리 벡터
∑: 3x3 공분산 행렬 (크기와 방향성을 조정)

3D 공간상에 수 많은 3D Gaussian이 모여 하나의 Scene을 구성하고 있다라고 생각하면 됩니다.
3D Gaussian 개념에 대한 더 자세한 글을 추후 작성할 예정입니다.

Rasterization 과 Ray-marching

기존의 3D data representation 방법들은 mesh나 point를 주로 이용하였는데, 이는 3D 공간을 explicit하게 표현하는 것으로, GPU/CUDA 기반의 빠른 rasterization (=3D object를 2D pixel screen으로 display)에 잘 맞기 때문에 활발하게 연구되었습니다.

조금 더 설명하자면, 가상의 triangle이나 polygon의 mesh로 3D model object를 생성하고, 각 triangle/polygon는 corner (=vertices)로 이루어져 있다. 이 mesh에는 3D 공간에서 position, color, texture와 normal vector 등의 정보가 저장되어있습니다. 그리고 이 triangle/polygon를 pixel 값으로 convert해서 우리가 2D computer screen으로 볼 수 있게 되는 것입니다.

Rasterization 기반 방법들은 각 point들을 최대한 한꺼번에 작업하려고 하기 때문에 속도가 빠르다는 장점이 있습니다다. 반면에 이 픽셀끼리 독립적으로 연산이 수행되므로 투명한 물체의 표현이나 겹친 부분 등을 표현할 수 없다는 단점이 있습니다.

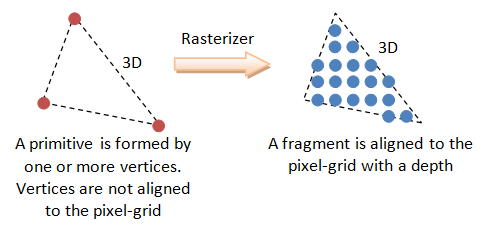
NeRF는 3D scene을 continuous scene으로 표현하였으며, volumetric ray-marching을 활용하여 MLP를 학습함으로써 3D 공간을 implicit하게 표현합니다.

NeRF는 기본적으로 physics 기반의 방법으로, 현실에서 물체에 비친 ray를 통해 눈에 상이 맺히는 과정을 묘사하여 3D scene을 최적화합니다. 특히 continuous representation의 가정은 이러한 optimization에 큰 도움이 됩니다.

가장 최신의 NeRF 모델들은 이러한 continuous representation을 위해, voxel grid (Plenoxels)나 hash grid (InstantNGP) 혹은 point 내에서 정의된 feature들을 interpolation하는 방식을 사용하곤 합니다.

하지만 NeRF는 rendering시 각 ray마다 3D point를 stochastic하게 sampling하는 과정이 매번 필요해서 training 및 rendering time cost가 크며 noise도 생기기가 쉽습니다.

3D Gaussian Splatting은 Rasterization과 Ray-Marching의 장점을 모두 가지는 3D gaussian 기반의 모델을 제안합니다.

3D gaussian representation를 통해 SOTA visual quality와 reduced training time을 달성할 수 있었고, Tile-based splatting solution을 통해 고화질에서 real-time rendering을 수행할 수 있었다고 합니다다.

위 논문의 방법론은 3가지 main component로 구성됩니다.

3D gaussian을 통한 scene representation

SfM process에서 추출된 point cloud를 초기 initial set으로 활용
3D gaussian은 differentiable volumetric representation이 가능
α-blending을 통해 NeRF와 비슷한 image formation model을 활용하여 3D to 2D projection을 효율적으로 수행 가능

3D gaussian properties의 최적화

이 방법에서 최적화는 3D gaussian의 3D position, opacity α, anisotropic covariance (gaussian의 shape와 spread), spherical harmonic coefficient (lightening과 shading)에 대한 최적화를 포함
위의 특성들을 최적화할때, adaptive density control을 사용하여 gaussian을 추가하거나 제거하는 과정을 거치는데, 이를 통해 compact하고 precise한 representation을 수행 가능

Real-time rendering

GPU sorting algorithm과 tile-based rasterization을 활용
Tile-based rasterization은 이미지를 몇 개의 tile block으로 나누어 각 tile을 독립적으로 rendering하여 속도가 빠름
3D gaussian representation의 특성 덕분에 각 splat (=gaussian)이 어떤 방향성을 가지게 되는데 (anisotropic splatting), 이러한 3D gaussian들의 shape와 orientation이 2D screen으로 projection될 때 반영되기 때문에, 더욱 현실적인 표현이 가능해지고, fast/accurate backward pass가 가능

2. Overview

위 논문의 전체적인 흐름은 다음과 같습니다.

Initialization : COLMAP과 같은 SfM알고리즘은 Camera Pose뿐만 아니라 Point Cloud 정보도 같이 얻을 수 있습니다. 이 Point Cloud들이 3D Gaussian의 초기 값으로 사용됩니다.
Projection : 3D Gaussian이 (Camera에서 z축으로 거리가 1만큼 떨어진) Image Plane으로 Projection되어 2D Gaussian형태가 됩니다. 이 과정은 GT 입력 이미지와 비교하여 parameter를 업데이트하기 위함입니다.
Differentiable Tile Rasterizer : 미분 가능한형태의 Tile Rasterization을 통해 2D Gaussian들을 하나의 Image로 생성합니다.
Gradient Flow : 생성된 이미지와 GT 이미지의 Loss를 계산하고 Loss만큼 Gradient를 전파합니다.
Adaptive Density Control : Gradient를 기반으로 Gaussian의 형태를 변화시킵니다.

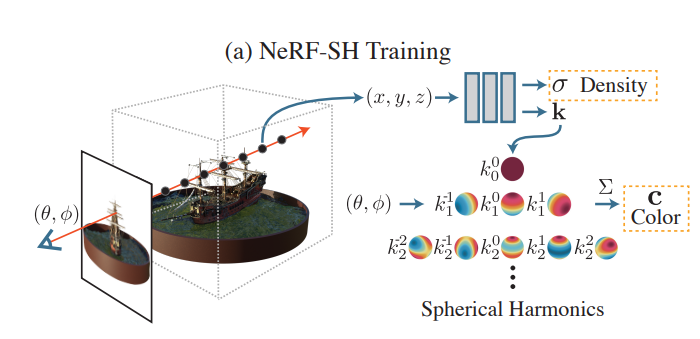
이때 각 gaussian의 color(directional appearance)는 spherical harmonics (SH)를 통해 표현됩니다.

Spherical harmonics(SH)

Spherical harmonics(SH)에 대해 간단하게 설명하고자 합니다. Spherical harmonics(SH)는 원래 양자역학에서 주로 사용되는 방법이고, Computer graphics 분야에서는 directional appearance (color) 값을 계산할 때 자주 사용되는 방법입니다.

이는 구면 좌표계에서 laplace equation의 해를 표현하는 방법으로, 구의 표면에서 polar angle θ와 azimuthal angle ψ로 정의되는 함수이다.

여기서 Laplace equation $∇^2 ϕ$ 는 spherical coordinate에서 다음과 같이 정의할 수 있습니다.

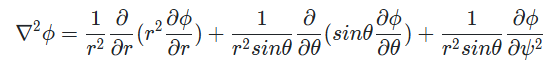
이에 대한 solution이 spherical harmonics로 표현될 수 있습니다. 다시 말해, spherical harmonics가 solution의 basis역할을 수행하게 됩니다. 이때, l은 degree, m은 order로, $−l≤m≤l$ 를 만족한다.

이때 이 spherical harmonics를 서로 다른 degree에 대해서 visualize하면 아래와 그림과 같다. 구의 표면에 다양한 intensity와 direction을 가지는 pattern으로 표현됩니다.

spherical harmonics는 서로 orthogonal하며, 구의 표면에서 정의된 어떤 함수도 unique하게 표현할 수 있습니다. 쉽게말해, light distribution의 복잡한 shape과 pattern을 finite term으로 쉽게 표현할 수 있습니다.

이러한 이유로 최근에는 많은 연구가 이러한 개념을 사용하여 서로 다른 각도에서 light interaction을 고려한 color를 표현하고 있으며, 이번 논문도 이 개념을 차용합니다.

다시 본문의 내용으로 돌아와 Rendering을 위해서는 이 3D gaussian을 2D로 projection 시켜야하는데, 아래와 같이 viewing transformation W를 통해 camera coordinate에서 2D covariance matrix $Σ ^′$ 를 얻게 됩니다.

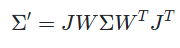
여기서, $J$ 는 Jacobian 행렬이다.

이 때, Covariance matrix를 직접적으로 최적화 하기 위해서는 Σ가 positive semi-definite 조건을 가지고 있어야 한다. 만약 해당 조건을 충족하지 못하고 최적화를 시킨다면 잘못된 optimizing을 할 수도 있게 된다.

이러한 문제를 해결하기 위해 저자들은 이 covariance matrix의 표현을 바꿔주는 방식을 택했는데,이를 위해 scaling matrix $S$ rotation matrix $R$ 을 사용하여 더 직관적이고 표현력이 높은 $Σ$ 를 구성하였다.

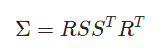
이 변환은 기존의 공분산이 가지는 의미를 통해 이해를 할 수 있다. 3D Gaussian에서 공분산은 타원체의 shape과 방향을 조정하는 역할을 하기 때문에 이는 Scale과 Rotation matrix만을 통해 표현이 가능하다는 것이다.
공분산의 대칭성 성질을 유지하기 위해 $S$ 와 $R$ 을 통해 표현할 때 전치행렬도 같이 곱해주어 공분산의 대칭행렬 성질을 그대로 유지하게 된다.

이렇게 Gaussian splatting 방법은 anisotropic covariance를 통해 scene을 표현하는데, 각 gaussian이 uniform한 구형이 아니고 서로 다른 spread와 direction을 가지고 있으므로 더욱 복잡한 geomery를 정확하게 표현할 수 있게 됩니다.

위의 그림에서 가장 오른쪽 shrunken gaussians는 각 gaussian의 크기를 줄여서 overlap 없이 보여준 것으로, 각 gaussian이 서로 다른 shape과 orientation을 가지도록 최적화 됬다는 것을 보여주고 있습니다.

3. Optimization

위 algorithm은 Gaussian Splitting optimization의 전체 과정을 보여주고 있습니다.

Optimization은 rendering & comparing의 iteration으로 이루어지며, rendered image를 training dataset의 captured view와 비교하여 이를 기반으로 학습이 됩니다.

먼저 SfM point로부터 3D gaussian을 만들고, 초기 covariance matrix를 가까운 세 점으로부터 평균 거리 값으로 초기화합니다.

여기서 Loss는 아래와 같이 정의됩니다.

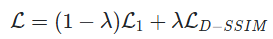
하지만 3D geometry의 2D projection의 모호함 때문에, geometry가 잘못 위치한 경우 이 geometry를 파괴하거나 움직일 수도 있어야 하는데, 이 부분을 Adaptive Control of Gaussian라고 합니다.

Adaptive Control of Gaussians

Scene에 맞게 3D Gaussian들을 adaptive하게 변형시키는 단계입니다. 이 부분은 논문에 따르면 100iteration마다 수행됩니다. 3D Gaussian이 Remove/Split/Clone하게 되는데, 이를 densification한다라고 표현하고 있습니다.

Remove Gaussian : 특정 threshold(=ε) 보다 낮은 alpha값(=α=투명도)을 가진 Gaussian은 제거 됩니다. 코드상에 threshold는 0.005로 되어 있습니다.

위 그림은 densification process를 보여주고 있습니다.

Remove Gaussian을 단계를 거친 후, Geometric feature를 파악하지 못한 영역(=Under-reconstruction)을 처리하고, 넓은 영역을 광범위하게 모델링한 Gaussian들(=over-reconstruction)에 대해 처리하게 됩니다. 구체적으로 Under/Over-reconstruction영역은 공통적으로 view-space positional gradient가 큰값을 가지기 때문에, view-space position gradient의 average magnitude(평균 크기)가 특정 Thresould(=0.0002)이상이 된다면, Gaussian들을 Clone 또는 Split합니다.

Clone Gaussian : Under-Reconstruction 영역에 대해서, 작은 크기의 (=covariance가 작은) 3D Gaussian들은 같은 크기로 copy되고, positional gradient의 방향에 배치되게 됩니다.

Split Gaussian : Over-Reconstruction 영역에 대해서, 큰 크기의 (=covariance가 큰) 3D Gaussian들이 작은 Gaussian으로 분해됩니다. 1개의 Gaussian을 2개의 Gaussian으로 분리하게 되는데, scale을 1.6(=실험적으로 결정한값)으로 나누는 형태로 계산됩니다. 분리된 Gaussian의 위치는 초기 Gaussian의 확률밀도값에 따라 배치되어집니다.

Clone의 경우 system의 총 volume과 gaussian의 갯수가 둘 다 증가하는 반면, split은 총 volume은 유지한 체 gaussian의 갯수만 늘어납니다. Optimization이 진행되면서 camera와 가까운 영역에 floater로 인해 gaussian의 갯수가 계속해서 늘어나게 됩니다.

이러한 현상을 막기 위해서 매 3000 iteration마다 α를 0에 가까운 값으로 초기화해줍니다. 이렇게 하면 다음 100 iteration 후 pruning을 통해 필요없는 gaussian들을 다시 제거할 수 있으며, 너무 큰 gaussian들이 중첩되는 경우도 잘 제거해줌으로써 전체 gaussian의 갯수를 잘 조절할 수 있게 됩니다.

4. IMPLEMENTATION, RESULTS AND EVALUATION

Mip-NeRF360은 A100 4장을 사용하였고, 나머지는 A6000을 사용했다고 합니다. FPS는 랜더링 시간을 의미합니다. 3D Gaussian Splatting을 Instant-NGP와 비교하였을 때 Train속도가 비슷하나, PSNR이 높고, 무엇보다도 랜더링 속도가 매우 빠릅니다.

PSNR (Peak Signal-to-noise ratio)

PSNR은 영상 화질 손실양을 평가하기 위해 사용되는 지표입니다. 이미지 저장, 전송, 압축, 영상 처리 등에서 영상 화질이 바뀌었을 때 사용됩니다.

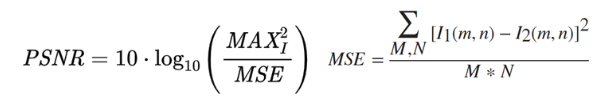
MSE는 작을수록 좋고, PSNR은 클수록 좋습니다.
MSE(Mean Square Error)는 가장 단순한 모델로써, 원본 이미지와 비교 이미지간의 각 Pixel 오차를 계산합니다. -> 오차가 작을수록 2개의 이미지가 유사합니다.
(M,N은 width, height를 의미하고, I(m,n)은 m,n좌표의 color값을 의미합니다.)
PSNR에서는 MSE가 분모로 들어감으로써, MSE가 작아 질수록 PSNR값이 커집니다.
-> PSNR이 클수록 손실양이 적고 퀄리티가 좋다는 것을 의미합니다.
MAX는 1개 픽셀당 갖고 있는 정보량(흑백 : 255, RGB : 255x3, RGBA : 255x4)을 나타냅니다.
-> MSE를 픽셀 정보량으로 Scale을 변경(Normalization)한다고 생각 할 수 있습니다.
픽셀간의 단순 오차를 나타내는 것이 MSE이고, MSE의 Scale을 변경(Normalization) 한 것이 PSNR라고 생각 할 수 있습니다.

SSIM (Structural Similarity Index Measure)

PSNR과 같이 변형된 영상의 화질 손실양을 평가하기 위해 사용됩니다.

SSIM값이 높을수록 좋은 수치입니다.
두 이미지(x, y) 간의 상관계수를 Luminance(휘도), Contrast(대비), Structure(구조) 총 3가지 측면에서 평가합니다. (α=β=γ=1)
** 휘도는 빛의 밝기, 대비는 밝기 차이, 구조는 상관관계를 나타냅니다.

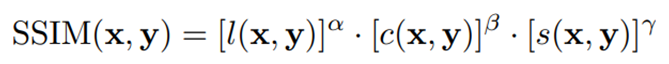
LPIPS (Learned Perceptual Image Patch Similarity)

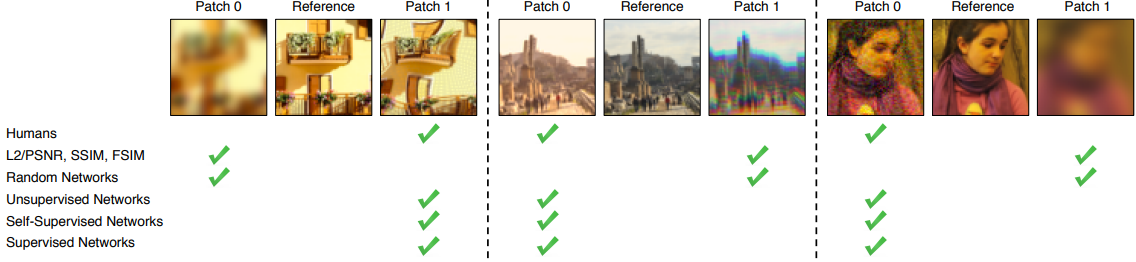
LPIPS는 Classification Task를 Supervised, Self-supervised, Unsupervised 딥러닝 모델로 학습하고, 비교할 이미지 2개를 각각 학습된 Network를 사용해 deep feature(Activation 결과값)를 추출하고, 이를 비교하여 유사도를 평가합니다. 기존 방법론 보다 좀더 perceptual하게 이미지들의 유사도를 평가할 수 있다고 합니다.

FPS의 경우에도 InstantNGP와 MipNeRF360에 비해 상당히 좋습니다.

Limitations

입력 이미지가 부족한 Sparse Scene에서 artifact가 발생하게 됩니다. Anistropic Gaussian이 많은 이점을 가졌지만, 길어지는 artifacts 또는 얼룩이 있는 Gaussian이 만들어 질 수 있습니다. (다른 연구들도 이런 현상이 있었다고 합니다.) Optimization을 통해 Large Gaussian을 만들 때 artifact가 가끔 발생하게 됩니다. Pose에 따라 다른 apperance를 보여주는 영역에서 주로 발생합니다.

이러한 artifact가 발생하는 이유는 다음과 같다.
1. Rasterizer단계에서 guard band를 거친 Gaussian trivial rejection입니다. 좀 더 이론적인 culling 접근법을 사용한다면 artifact를 완화 할 수 있을 것입니다.
2. depth/blending order를 갑작스럽게 switching하는 Gaussian을 만들 수 있는 간단한 visibility algorithm입니다. 이것은 antialiasing으로 해결 되어 질 수 있을 것이며, 미래 연구로 남겨두었다고 합니다.

마지막으로

이 논문은 올해부터 공부하는 랩실에서 처음 배운게 된 논문이었다. DL/ML에 대한 기본적인 개념만 배웠다가, 이 논문을 공부하게 되었는데 새로운 개념들이 너무 많았지만 같이 공부를 하면서 생성형 이미지 분야에 대한 많은 공부가 된 것 같다.
NeRF, Rasterization이나 Spherical harmonics의 개념을 공부해볼 수 있어서 좋았고, 관련해서 리뷰를 해보고 싶다.