문제 탐색하기

입력 자료 정리

1. 처음 입력값 T는 테스트 케이스로 이후 입력하는 값의 개수이다
2. 이후 T만큼 들어오는 값은 찾고자 하는 괄호 문자열의 길이로 각 입력은 독립적이다

해결방법 추론

1. 각 순번마다 '('나 ')'을 선택하고 입력받은 괄호 문자열의 개수만큼 반복한다
2. DFS로 1번 방법을 구현할 수 있는데, 문제는 시간복잡도를 계산했을 때 시간초과가 발생한다
3. 5000^2 X 100은 2억 5천으로 시간제한 2초를 초과하기 때문에 다른 방법을 필요하다
4. 다시 생각한 방법은 1번 방법을 유지하면서 그 과정을 기록하는 DP방법이다
5. 미리 5000^2만큼 계산해서 구한다음, T만큼 순회해서 구한다면 정답이 시간초과는 발생하지 않을 것이다
6. 하지만 이렇게 할 경우, 재귀문에서 너무 많은 함수가 호출되어서 메모리 초과가 발생할 것이다
7. 따라서 해당 방법도 해결방법으로 선택할 수 없다
8. DP라는 키워드를 바탕으로 규칙을 찾기 위해 올바른 괄호 문자열을 만들 수 있는 경우를 직접 계산해봤다
9. 일단 홀수번째는 절대 성립할 수 없다. 오로지 짝수번째일때만 올바른 괄호 문자열이 생성된다
10. 0번째와 2번째는 반드시 1가지 경우만 가능하다. 또한 0번째가 가능하므로 괄호가 없는 경우도 올바른 괄호 문자열로 확인할 수 있다
11. 4번째 6번째 8번째까지 경우의 수를 생각했을 때, 2개, 4개, 8개인 것을 확인했다
12. 짝수번째마다 이전 값의 2배씩 늘어난다. 이점을 이용한다면 다음과 같이 점화식을 세울 수 있다
    점화식: dp[i] = dp[i-1] * 2;
13. 미리 DP배열에 L의 최대값인 5000까지 계산해둔 다음 테스트케이스마다 출력한다면
    시간초과와 메모리 초과없이 문제를 해결할 수 있을 것이다!

시간복잡도 계산

1. 위 방법으로 했을 때 시간복잡도는 다음과 같다
   시간복잡도: O(5001)
2. 따라서 시간초과없이 문제를 해결할 수 있다!

코드 설계하기

입력값 상태 관리

1. 먼저 1차원 dp배열을 5001크기로 생성한다. 타입은 long타입으로 지정한다
2. 이후 들어오는 T와 각 L입력값은 변수로 관리한다

구현코드 설계

1. DP의 2번 인덱스는 1로 초기화하고, 4부터 짝수만큼 증가하며, DP식을 갱신한다
2. 이때 1_000_000_007 모듈러 연산을 함께한다
3. DP식은 앞서 설계한 점화식을 기준으로 구현하면 됩니다.

출력값 설계

1. T만큼 들어온 각 L을 DP의 인덱스로 해서 값을 출력하면 정답이 될텐데..

시도 회차 수정

1회차 시도 실패 코드

import java.io.*;
import java.util.*;


public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        long[] dp = new long[5001];
        dp[2] = 1;
        for (int i = 4; i < 5001; i+=2) {
            dp[i] = dp[i-2]*2 % 1_000_000_007;
        }
        int T = Integer.parseInt(br.readLine());
        for (int i = 0; i < T; i++) {
            int a = Integer.parseInt(br.readLine());
            bw.write(dp[a] + "\n");
        }


        br.close();
        bw.close();
    }

}

1회차 시도 실패

1. 25%에서 틀렸습니다가 나왔다.
2. 원인이 무엇일까 분석해보니 점화식을 잘못 세웠다
3. 6번째와 8번째 가능한 경우가 더 있었다. 각각 4 -> 5, 8 -> 14로 경우의 수가 늘어난다
4. 또한 규칙을 다시 확인해보니 6번째를 기준으로 했을 때,
   이전 짝수인덱스들 즉 0,2,4번째 올바른 괄호의 경우가 6번째에서 활용되는 것을 확인했다
5. L의 크기가 5000이므로 이중포문이 가능하다.
   따라서 i를 기준으로 이전 짝수 인덱스를 합산하는 방식의 점화식을 다시 세웠다
6. 점화식: dp[i] += dp[j] * dp[i-(j+2)]
7. 해당 점화식에 모듈러 연산까지 추가하면 이제 해결가능할 것이다!
8. 또한 1차 시도에서 dp[0]을 1로 초기화하지 않았다.
9. 2회차 시도에서 8번 로직을 추가했다.

2회차 시도 코드

import java.io.*;
import java.util.*;

/**
 * 풀이 과정:
 *
 * 해결방법:
 *
 * 시간복잡도: O()
 * 공간복잡도: O()
 *
 */
public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        long[] dp = new long[5001];
        dp[0] = 1;
        dp[2] = 1;
        for (int i = 4; i < 2501; i+=2) {
            for (int j = 0; j < i; j+=2) {
                dp[i] += (dp[j] * dp[(i-(j+2))]) % 1_000_000_007;
            }
        }
        int T = Integer.parseInt(br.readLine());
        for (int i = 0; i < T; i++) {
            int a = Integer.parseInt(br.readLine());
            bw.write(dp[a] + "\n");
        }


        br.close();
        bw.close();
    }


}

2회차 시도 실패

1. 이번에도 25%에서 실패했습니다가 나왔다.
2. 내가 발견하지 못한 규칙이나 경우의 수가 더 있는 것도 아니라서 방법 자체가 틀린 것인지 고민했다
3. 하지만 놀랍게도 실패의 원인을 모듈러 연산에서 발견했다
4. 모듈러 연산을 합산할 때 점화식과 함께 계산하면, 합산하는 값만 모듈러 연산이 적용된다
5. 즉 이전에 누적된 dp의 값은 모듈러 연산이 적용되지 않는다!
6. 따라서 모듈려 연산을 점화식 이후로 분리했다

3회차 시도 성공!

1. 해당 코드로 제출했을 때, 문제 없이 통과했다!

정답코드

import java.io.*;
import java.util.*;

public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        long[] dp = new long[5001];
        dp[0] = 1;
        dp[2] = 1;
        for (int i = 4; i < 5001; i+=2) {
            for (int j = 0; j < i; j+=2) {
                dp[i] += (dp[j] * dp[(i-(j+2))]);
                dp[i] %= 1_000_000_007;
            }
        }
        int T = Integer.parseInt(br.readLine());
        for (int i = 0; i < T; i++) {
            int a = Integer.parseInt(br.readLine());
            bw.write(dp[a] + "\n");
        }


        br.close();
        bw.close();
    }


}

번외: 카탈란 수

1. 문제 해결 이후 또다른 풀이가 있을까 찾아보다가 해당 점화식이 카탈란 수 점화식이라는 것을 확인했다
   
2. 카탈란 수를 이용하면 위와같이 올바른 괄호 쌍을 만들 수 있고, 아래와 같은 점화식을 얻을 수 있다
   
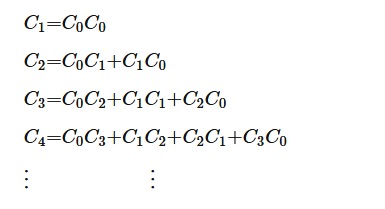
3. 앞선 시도회차에서 세운 dp[i] += (dp[j] * dp[(i-(j+2))])점화식이 위 카탈란 수 점화식과 같다는 것을 확인할 수 있다! (카탈란 수의 번호를 짝수번째 번호 순서로 생각하면 일치한다!)
4. 이후 유사한 문제가 나온다면 카탈란 수 점화식을 떠올려서 문제를 해결하면 될 것이다!

문제 링크

10422번 - 괄호

참고

• 카탈란 수 개념