백준 #9095 1, 2, 3 더하기

본 포스팅은 Java 풀이법입니다.

접근법

정수 n을 1, 2, 3의 합으로 만들 수 있는 경우의 수를 구하는 것이 핵심이었다.
즉, 하나의 수를 만드는 방법이 그보다 작은 수들을 조합한 결과로 이루어질 수 있다는 뜻이다.

이처럼 어떤 큰 문제(n)를 풀기 위해서, 더 작은 문제(n-1, n-2, n-3)들의 결과를 조합해서 해결할 수 있을 때, 이는 대표적인 동적 프로그래밍(DP) 문제로 볼 수 있다.

=> DP : 중복 계산을 방지하고 결과를 저장해두는 방식

---

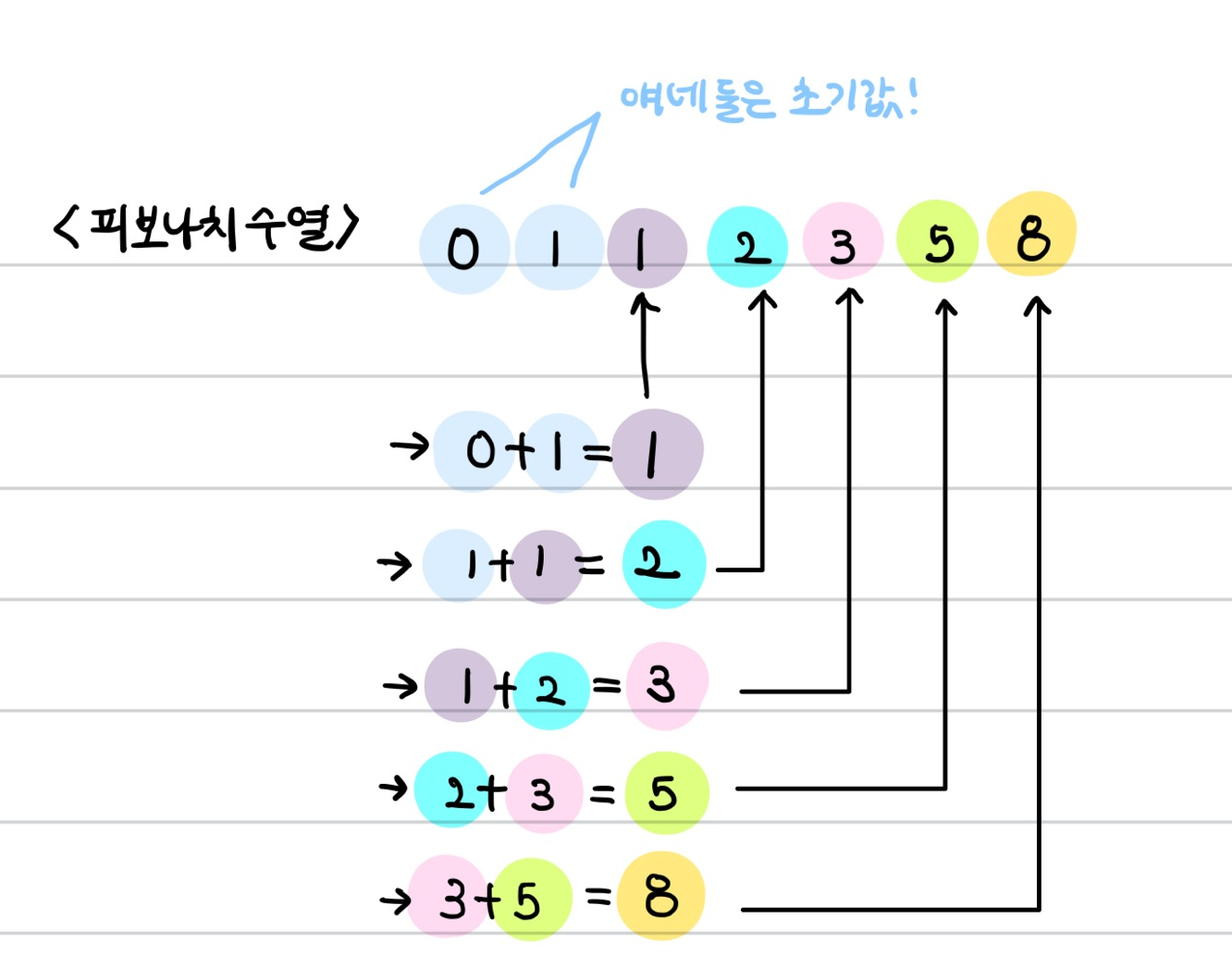
2. DP 중 Bottom-Up 방식의 대표 예시: 피보나치 수열

이 문제의 풀이 방식은 대표적인 Bottom-Up 방식의 DP와 유사한데,
가장 흔한 예시는 피보나치 수열이다.

f(0) = 0  
f(1) = 1  
f(n) = f(n-1) + f(n-2)   (n ≥ 2)

이처럼 작은 단위의 계산 결과를 차곡차곡 쌓아올려 전체 문제를 해결하는 방식을 이용하고자 했다. 아직까지는 이해가 잘 안될 수 있다..ㅠㅠ 아래 내용을 더 살펴보자.

---

3. 직접 예시를 써보자

초기에는 규칙이 보이지 않기 때문에, n값을 작게 두고 가능한 경우를 직접 나열해보았다.

n = 1 → [1] → 1가지  
n = 2 → [1+1], [2] → 2가지  
n = 3 → [1+1+1], [1+2], [2+1], [3] → 4가지  
n = 4 → [1+1+1+1], [1+1+2], [1+2+1], [2+1+1], [2+2], [1+3], [3+1] → 7가지

이렇게 정리해보면, 아래와 같은 점화식이 보이기 시작한다.

dp[1] = 1  
dp[2] = 2  
dp[3] = 4  
dp[4] = dp[3] + dp[2] + dp[1] = 4 + 2 + 1 = 7  
...

즉, n을 만들기 위한 경우의 수는
n-1, n-2, n-3을 만들 수 있는 방법에 각각 1, 2, 3을 더한 모든 조합과 같다.

그래서 최종적으로 다음과 같은 점화식을 도출할 수 있다.

dp[n] = dp[n-1] + dp[n-2] + dp[n-3]

단, 위 점화식을 사용하려면 dp[1], dp[2], dp[3]은 이미 값이 정해져 있어야 하므로
초기화가 필요한 부분은 직접 값을 넣어줘야 한다.

(초기화가 필요하다 = 규칙성이 존재하지 않아서 직접 값을 구해주고 해당 값으로 선언해놓아야 한다)

---

4. 자바 코드 및 주석 설명

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        int t = sc.nextInt();  // 테스트 케이스 개수 입력

        int[] dp = new int[11];  // n은 최대 10까지 입력되므로 dp[0] ~ dp[10]까지 준비

        // 초기값 설정 (규칙이 나오기 전 직접 세서 넣은 값)
        dp[1] = 1; // [1]
        dp[2] = 2; // [1+1], [2]
        dp[3] = 4; // [1+1+1], [1+2], [2+1], [3]

        // 점화식 적용: dp[n] = dp[n-1] + dp[n-2] + dp[n-3]
        for (int i = 4; i <= 10; i++) {
            dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
        }

        // 각 테스트 케이스마다 결과 출력
        for (int i = 0; i < t; i++) {
            int n = sc.nextInt();
            System.out.println(dp[n]);
        }

        sc.close();
    }
}