S.E.B 0.0.7

힙 HEAP

힙은 힙의 특성(최소 힙 Min Heap)에서는 부모가 항상 자식보다 작거나 같다) 을
만족하는 거의 완전한 트리 Almost Complete Tree 인 특수한 트리 기반의 자료구조다.

J.W.J 윌리엄스 John William Joseph Williams (1930.9.2 - 2012.9.29) , 영국의 컴퓨터 과학자가 1964년 힙 정렬 알고리즘을 고안하면서 설계

• 완전 이진 트리의 일종

  • 완전 이진트리 Complete Binary Tree

    • 완전 이진트리(Complete Binary Tree)는 노드를 삽입할 때, 왼쪽부터 차례대로 삽입하는 트리이다.

    • 예를들어서 [그림 1]의 경우는 완전이진트리가 맞지만, [그림 2]와 같은 경우는 완전 이진트리가 아니다.

      

      그림1) 완전 이진 트리 예 / 출처 : https://juhee-maeng.tistory.com/94

      

      그림 2) 불완전 이진 트리 예 / 출처 : https://juhee-maeng.tistory.com/94

• 우선순위 큐를 사용할때 활용

• heapq 모듈로 파이썬내에 구현되어 있음

  • 파이썬에는 최소힙만 구현되어 있음

• 최소 힙은 부모가 항상 자식 보다 작다 → 루트 값이 가장 작은 값을 갖게 된다

  • 우선순위 큐에서 가장 작은 값을 추출하는 것은 매번 힙의 루트를 가져오는 형태로 구현

• 우선순위 큐 ADT(추상 자료형)는 주로 힙으로 구현

  • 힙은 주로 배열로 구현
    • 따라서 우선순위 큐는 결국 배열로 구현되는 셈

힙은 정렬된 구조가 아니다. (반정렬 상태, 느슨한 정렬 상태)
최소 힙의 경우 부모 노드가 항상 작다는 조건만 만족하며 → 요소들은 서로 정렬되어 있지 않다.

• 요소가 정렬 되어 있지 않다는 것은?
  • 오른쪽의 노드가 레벨 차이에도 불구하고, 왼쪽 노드보다 더 작은 경우도 있음
  • 즉, 부모 자식 간의 관계만 정의할 뿐, 좌우에 대한 관계는 정의하지 않는다.

힙(heap)의 종류

• 최대 힙(max heap)
  • 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
  • key(부모 노드) ≥ key(자식 노드)
• 최소 힙(min heap)
  • 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리
  • key(부모 노드) ≤ key(자식 노드)

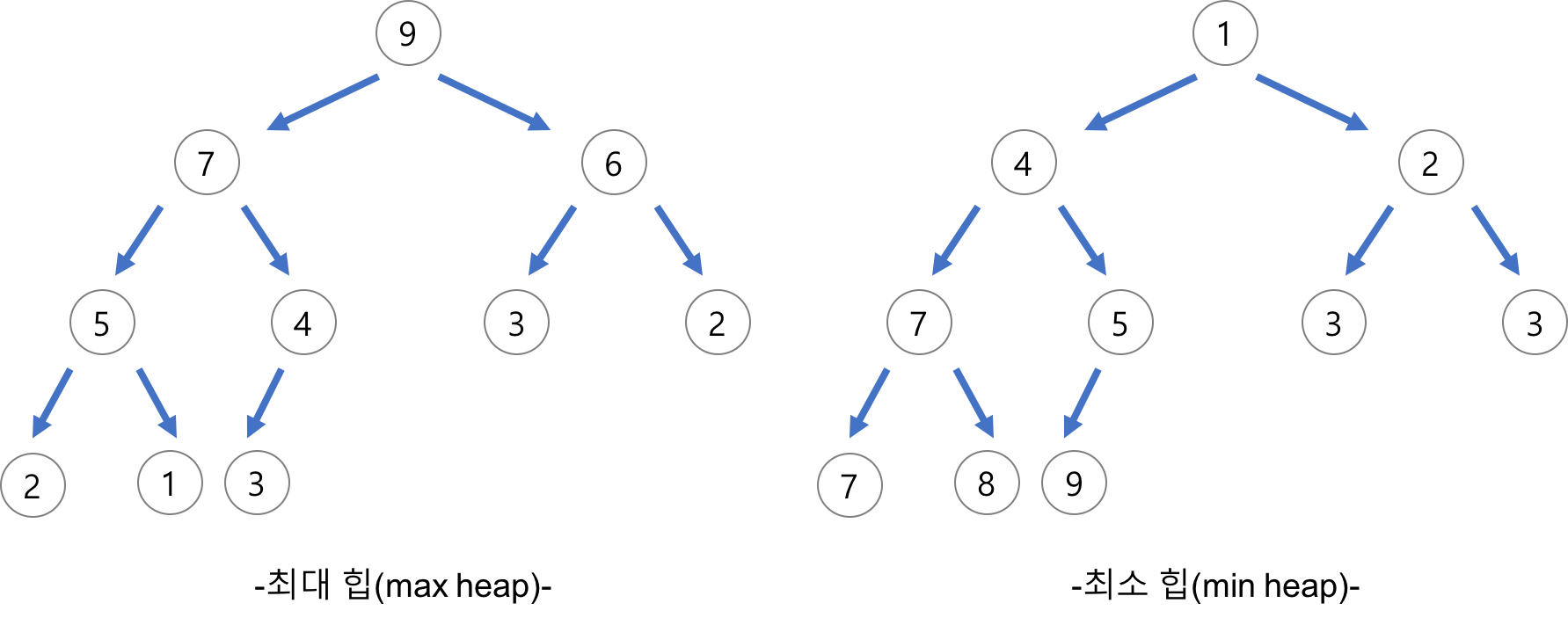
출처:https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html

이진 힙 Binary Heap

• 자식이 둘인 힙

이진힙의 배열 표현

• 완전 이진 트리형태의 이진 힙은 배열에 빈틈없이 배치가 가능
• 트리의 배열 표현의 경우 계산을 편하게 하기위해 인덱스는 1부터 사용 ( 앞서 문제풀이에서도 기본값을 주어줌)

힙의 활용 예시

• 우선순위 큐

• 다익스트라 알고리즘 구현

• 프림 알고리즘 Prim's Algorithm 구현

  프림 알고리즘 - 위키백과, 우리 모두의 백과사전

• 힙 정렬과 최소 신장 트리 Minimum Spanning Tree 구현

  • 최소 연결 = 간선의수가 가장 적다
  • n개의 정점을갖는 그래프의 최소 간선의 수는 (n-1)개이고, (n-1)개의 간선으로 연결되어 있으면 필연적으로 트리형태가 된다.
  • 스패닝 트리 중에서도 사용된 간선들의 가중치 합이 최소인 트리를 최소 신장 트리 MST라고 함

• 중앙값의 근사값 Approximation 구할 때

  • 부모-자식 관계가 정의되어 있는 완전 이진 트리이기 때문에 적절한 중간 레벨의 노드를 추출

힙 연산

• 이진 힙을 위한 클래스 정의

class BinaryHeap(object):
	def __init__(self):
		self.items = [None] #0번 인덱스를 사용하지 않기 위한 초기값 
	
	def __len__(self):
		return len(self.items) -1 # 메소드 호출시 최대 길이보다 하나 작은 값 리턴

삽입

업힙 up-heap

• 힙에 요소를 삽입하기 위한 방법
• percolate_up() 이라는 함수로 정의
  • 요소를 가장 하위 레벨(말단리프)의 최대한 왼쪽으로 삽입
    • 배열로 표현할 경우 가장 마지막에 삽입
    • 삽입은 insert() ⇒ (기존 heapq 모듈의 heapq.heappush() 와 대응)
  • 부모 값과 비교해 값이 더 작은 경우 위치를 변경
  • 계속해서 부모 값과 비교해 위치를 변경
    • 가장 작은 값일 경우 루트까지 올라감

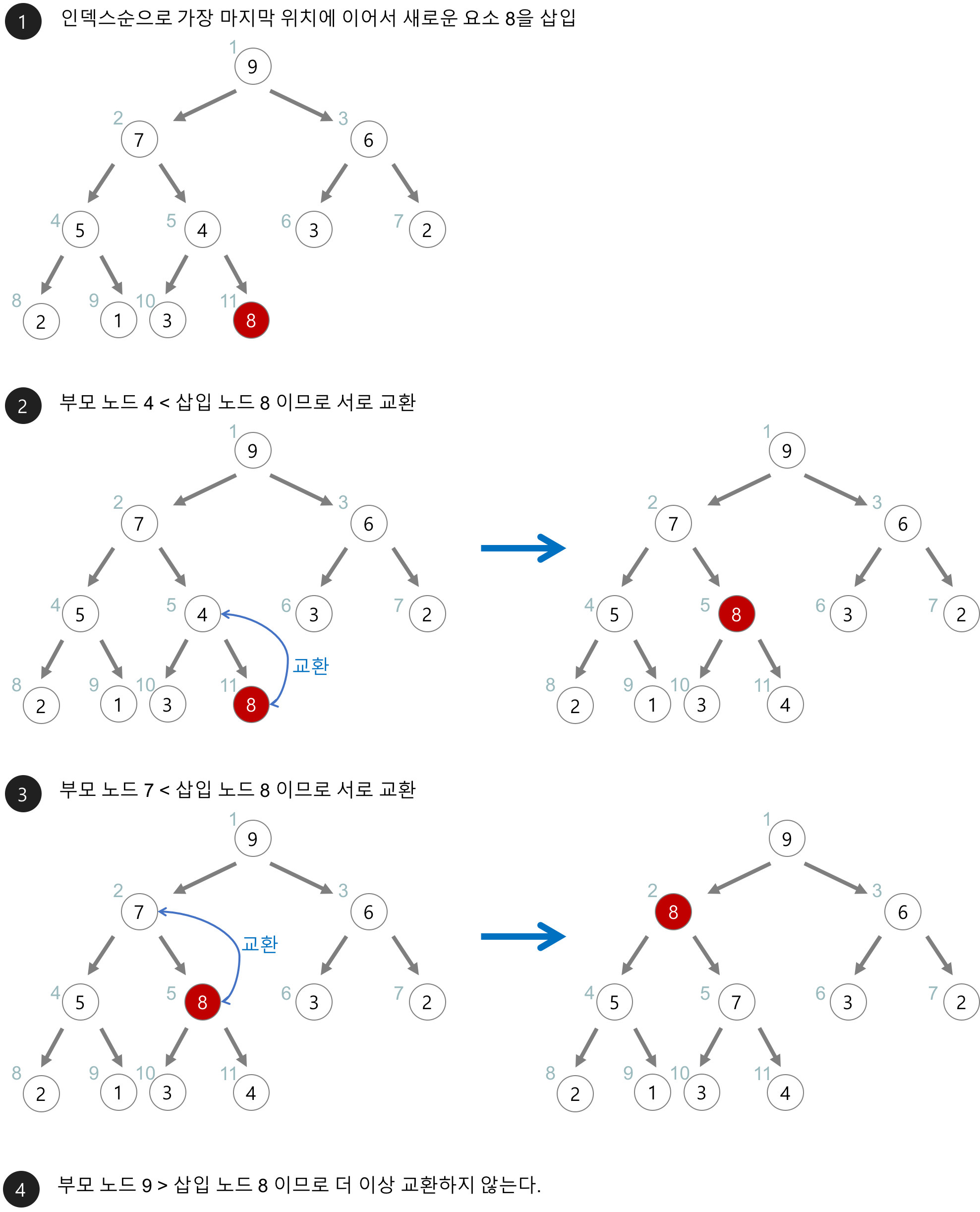
https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html

# percolate_up 함수 정의

# 1. data는 leaf 노드에 인서트 
# 2. binary heap의 조건( heap property ) 을 맞추기 위해 inserted data 는 점차 root 방향으로 올라간다.
# 3. 재귀적으로 반복

def _percolate_up(self): # '_' => PEP 8에 따른 내부함수표기
	
	i = len(self)
	parent = i // 2

	while parent >= 0: 
		if self.items[i] < self.items[parent]:
			self.items[parent], self.items[i] = self.items[i] , self.items[parent]
		
		i = parent
		parent = i // 2

#삽입 하기위한 insert 함수 정의
def insert(self, k)
	self.items.append(k)
	self._percolate_up()

추출

다운 힙 Down-Heap

• 루트를 추출하는 것
• 시간복잡도 = O(log n)
• 추출 이후에 비어 있는 루트에는 가장 마지막 요소가 올라가게 됨

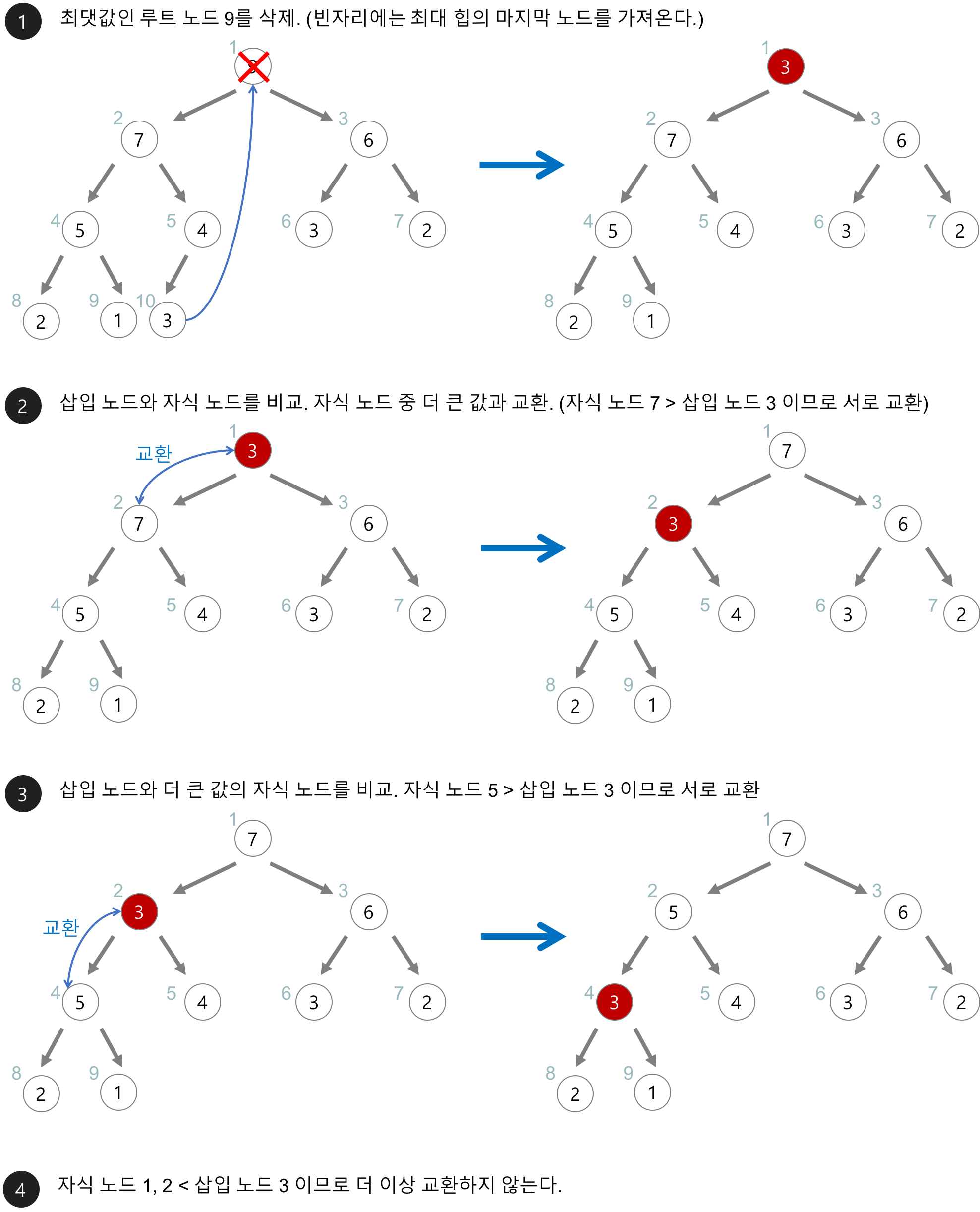
https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html
이진 힙에서요소의 추출 및 삭제

다운 힙 Down-Heap

• 자식 노드와 값을 비교해서 자식보다 크다면 내려가는 연산
• percolate_down() 이라는 함수로 구현
  • 추출자체는 extract() 함수 호출로 실행 (기존 heapq 모듈의 heapq.heappop() 와 대응)
  • 이후 루트 값이 추출 됨 → percolate_down()이 실행

def _percolate_down(self, idx):
	left = idx * 2
	right = idx * 2 + 1
	smallest = idx
	
	if left <= len(self) and self.items[left] < self.items[smallest]:
		smallest = left
	
	if right <= len(self) and self.items[right] < self.items[smallest]:
		smallest = right

	if smallest != idx:
		self.items[idx], self.items[smallest] = self.items[smallest], self.items[idx]
		self._percolate_down(smallest)

def extract(self):
	extracted = self.items[1]
	self.item[1] = self.items[len(self)]
	self.item.pop()
	self._percolate_down(1)
	return extracted

이진 힙과 이진 탐색 트리(BTS)

• 이진 힙은 상/하(부모/자식) 관계를 보장하고, 최소힙의 경우 부모가 자식보다 항상 작다.
  • 가장 큰 값을 추출하거나(최대 힙) , 가장 작은 값을 추출할 때(최소 힙) 사용
  • 우선순위와 관련된 문제에 사용
  • 시간복잡도는 모두 O(1)에 가능하다.
• 이진 탐색 트리(BTS) 는 좌/우 관계를 보장하고, 부모는 왼쪽 자식 보다 크고, 오른쪽 자식보다 작거나 같다.
  • 따라서 탐색과 삽입 모두 O(log n)에 가능하다
  • 모든 값이 정렬되어야 할 때 사용한다

전체코드

#이진 힙 클래스 구현
class BinaryHeap(object):
	def __init__(self):
		self.items = [None] #0번 인덱스를 사용하지 않기 위한 초기값 
	
	def __len__(self):
		return len(self.items) -1 # 메소드 호출시 최대 길이보다 하나 작은 값 리턴
	
#삽입 시 실행, 반복 구조 구현
	def _percolate_up(self): # '_' => PEP 8에 따른 내부함수표기
		
		i = len(self)
		parent = i // 2
	
		while parent >= 0: 
			if self.items[i] < self.items[parent]:
				self.items[parent], self.items[i] = self.items[i] , self.items[parent]
			
			i = parent
			parent = i // 2
	
	#삽입 하기위한 insert 함수 정의
	def insert(self, k)
		self.items.append(k)
		self._percolate_up()

	#추출시 실행, 재귀 구조 구현
	def _percolate_down(self, idx):
	left = idx * 2
	right = idx * 2 + 1
	smallest = idx
	
	if left <= len(self) and self.items[left] < self.items[smallest]:
		smallest = left
	
	if right <= len(self) and self.items[right] < self.items[smallest]:
		smallest = right

	if smallest != idx:
		self.items[idx], self.items[smallest] = self.items[smallest], self.items[idx]
		self._percolate_down(smallest)

	def extract(self):
		extracted = self.items[1]
		self.item[1] = self.items[len(self)]
		self.item.pop()
		self._percolate_down(1)
		return extracted