직관 ( GREEDY) → 완전 탐색( EXhausted Search) → 시간 , 메모리 부족 + 완탐 + Greedy [수학적으로 증명된 Greedy]
피보나치 수열
카탈란 수열
1. 명제와 논리
-
직관 → 탐욕적
-
명제 참과 거짓을 명확히 판별 할 수 있는 문장 → 발상의 전환 다른 방법으로 생각하라
p ⇒ q === ~q ⇒ ~ p이다로 생각
-
마방진은 각 행의 합, 열의 합 , 대각선들의 합이 모두 같다.
-
2로 나누어 떨어지면 짝수다
-
2로 나누어 떨어 지지 않으면 홀 수다
-
유리수는 서로소인 두 정수의 나눗셈으로 표현 할 수 있다.
-
유리가 아니면 무리수 이다.
-
0을 제외한 어떤 수 를 다른 수로 나우어 나머지가 0이면 A는 B의 배수이다., B는 A의 약수이다.
-
-
멍청이 논리 (pseuduo → proposition 논리) : 너가 경찰 서장이면 난 대통령이다!
→ 틀린 명제를 참이라고 가정을 하면 어떤 명제도 참이 된다
2가 홀수면 5는 짝수다.
-
증명
증명은 정확한 명제식으로 표현할 수 있는 것이라야함'
보통은 정확한 명제식 까지 쓰지 ㅇ는 않으나 근본적으로는 명제식으로 바 꿀 수 있음
증명에 대한 수많은 오해가 p→q를 p↔q와 혼동하는것에서 일어남
모두 만족해야한다 (증명 힘듬) ⇒ 하나라도 만족하지 않는 것 찾기 (증명이 쉬움)
-
수학적 귀납법과 증명의 수준 ( 코끼리를 냉장고에 넣은 방법)
수학적 귀납법의 기본형 : p(1)이 참이고 , P(n) → P(n+1)이 참이면 P(n)은 모든 자연수 N에 대해서 참이다.
수학적 귀납법의 강한 형태 : P(1)이 참이고 , P(1)^P(1)^P(1).......P(n)^P(n+1)이 참이면 P(n)은 모든 자연수 N에 대해서 참이다
-
증명 연습
-
시그마
Trival Proof : P(x) → Q(x)를 증명하려는데 Q(x)가 항상 참인 경우
문제 11. 자연수 N에 대해서 N^2 +5N +3은 항상 홀수임을 증명하라
→ 자연수 = (짝수 + 홀수) , N이 짝수인 경우와 홀수인 경우를 따로 증명한다
문제 12. N^2이 3의 배수이면 n은 3의 배수임을 증명하라
→ 대우 , 3의 배수가 아니면 3으로 나눈 나머지가 1 또는 2, N = 3K+1, 3K+2
문제 13. n이 홀수이면 N^2을 8로 나눈 나머지는 1임을 증명하라
→ N을 4로 나눈 나머지가 1인 경우 3인 경우로 나누어보자 ⇒ N = 4K+1 , 4K+3
이항정리( 찾아서 해볼것)
a0 90 + a1 91 + a2 92 ⇒ (1+8)^N = → A0+A1+A2+A3....⇒이 된다
n(n+1)(n+2) , (n-1)(n)(n+1) 모두 연속인 세수는 6의 배수이다 (*외우기)
-
-
-
수와 표현
짝수 2n ( 4n , 4n+2)
짝수 2n+1( 4n+1, 4n+3)
정사각형 마방진 = 짝수, 마방진 +홀수 마방진 = 짝수 (4n 마방진, 4n+2마방진) =2n+1 마방진
n(n+1)(n+2) , (n-1)(n)(n+1) 모두 연속인 세수는 6의 배수이다 (*외우기)
[n] 가우스 n을 넘지 않는 최대 정수 ⇒ 자바 자체가 가우스
9%2 = 9-[9%2]*2=1
[log10 n] 자리수를 구할때 → [log10 123] =2 ⇒ (int) log10 n
⇒ F(123) = 321로 바꾸어라 ⇒ f(n) = (n%10)+ f(n/10)
[9/2] ⇒ 9/2 프로그래밍 정수 연산 ⇒ (int) 캐스팅 연산
완전수 ( 자신을 제외한 약수의 합이 자신이 되는 수 )
친화수 ( a자신을 제외한 약수의 총합이 B가 되고 , B 자신을 제외한 약수의 총합이 A가 되는 수)
스미스 ( 각 자리의 합이 소인수 분해 했을 떄읭 각 자리수의 합과 같은 수 22 = 2*11 ⇒ 2+2 = 2+1+1, 소수 제외)
약수 (swea 8567)
제곱
소수 에라토스 테네스 체
-
유클리드 호제 ( 백준 톰과제리 , SWEA 7466)
최소 공배수, 최대 공약수
확장 유클리드 → 120x+ 150y = 30 ⇒ 4x +5y= 1 ( bezout's identitiy)
확장 유클리드 호제 ⇒ 실습해보기
-
소인수 분해
n! 과 소인수 분해 ( 배열)
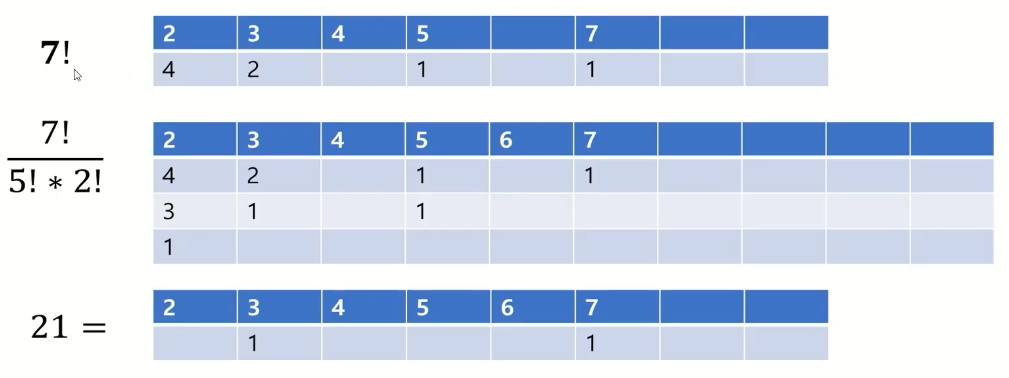
.png)
소수로 어떤 수를 나누면 항상 주기가 있다
## 페르마 소 정리 공부하기
## nCr을 구하라
GCD vs LCM
배열 위치 이동
### 1차월 배열을 2차원 배열로 바꾸는 연산
**A[i] ⇒ B[i/col][i%col]**
아이 나누기 칼럼 아이 모둘러 칼럼
아나칼 아모칼
### 2차월 배열을 1차원 배열로 바꾸는 연산
**A[i][j] ⇒ B[i*col+j]**
아이 곱하기 칼럼 더하기 제이
알카제이-
벡터
내적, 외적
외적 > 0보다 크면 CCW는 맛있어
삼각형 넓이 구하는 법
Convex Hull
-
주어진 점들 중 y좌표가 가장 작거나 혹은 가장 작은 점이 둘 이상이면 x 좌표가 가장 작은 점을 선택한다
-
선택학 점을 기준으로 나머지 점들을 반시계 방향으로 정렬(각도 + 거리)
-
그라함 스캔 알고리즘 적용
Graham's scan algorithm
-
제일 처음 선택한 점을 스택에 먼저 넣고 정렬된 점들을 차례대로 스택에 넣는다.
-
새로운 점을 스택에 push할 때, 만약 스택에 두개 이상의 점이 있다면 가장 최근에 push된 두 점을 이은 직선을 기준으로 새로운 점이 왼쪽에 있다면 push, 오른쪽에 있다면 스택의 가장 위의 점을 pop
-
- 함수
.png)
- 함수의 개수
X-Y로의 함수의 개수 n^M
- 일대일 함수 ( 단사 )
정의역에 있는 서로 다른 원소를 공역에 있는 다른 원소를 mapping
nPm
- 일대일 대응(전단사) -역함수가 존재한다.
n!
- 기본 수열과 특성 방정식
등차 수열
- 각항이 초항과 일정한 차를 가지는 수열
- 일반항 → 수열에서 n번째 항 ( N은 자연수) 수열의 모든항을 N에 대한 식으로 나타낸것
Sn = a1 + a2 + a3 + a4 ..... an
Sn= an + an-1+ ..... a1
2Sn = n(a1+an)
Sn = n(a1+an) / 2
등비 수열
- 각 항이 초항과 일정한 비를 가지는 수열
- 1, 2 , 3 ,8 ,16

계차 수열

특성 방정식

나머지 정리 (MOD P)
- 덧셈의 나머지 정리
(a+b) % p = ( a%p + b%p ) % p
- 뺄셈의 나머지 정리
(a- b) % p = ( a%p - b%p ) % p - 곱셈의 나머지 정리
(ab) % p = ( a%p b%p ) % p - 나눗셈은 나머지정리 불가능 -> 페르마의 소정리
(a 1/b) % p = (ab^(p-2)) % P
=> (a%p * b^(p-2) % p ) % P
