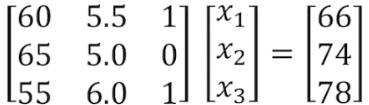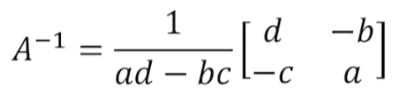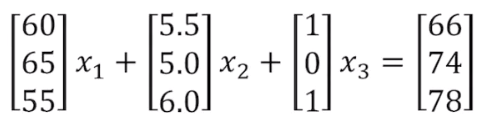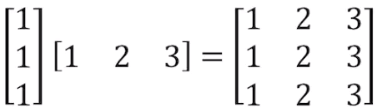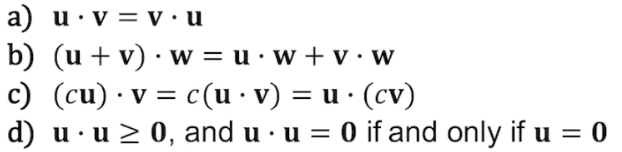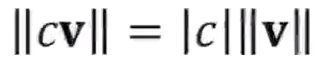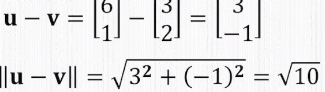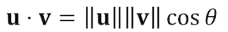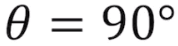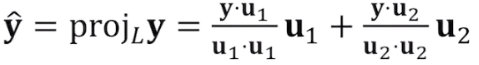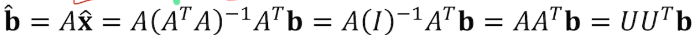https://www.boostcourse.org/ai251/joinLectures/195088
2. 선형시스템 및 선형변환
Matrix Equation
Identity Matrix, 항등행렬
어떤 벡터와 곱해도 자기 자신을 도출해내는 행렬
Inverse Matrix, 역행렬
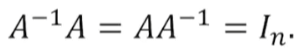
- 정사각행렬에서만 해당한다.
- ad-bc = 0 이면 역행렬이 존재하지 않는다.
판별색 ad-bc = det A라고 부른다.
역행렬이 존재하지 않는 경우
해가 무수히 많거나, 해가 존재하지 않는다.
m x n 행렬에서
- m < n : 해가 무수히 많음 (방정식의 수 < 미지수의 갯수)
- m > n : 해가 존재하지 않음 (방정식의 수 > 미지수의 갯수)
- m = n : 해가 존재 (정사각행렬)
Vector Equation
Span
벡터들로 만들 수 있는 모든 선형 결합
가중치를 조절하여 적당한 조합을 선택하기 위한 단계
Span{V1, V2}에서, V3 = 2V1 + 3V2, a, b= 상수 일때, Span{V1, V2} = Span{V1, V2, V3} 이다. 이 경우 선형 종속이다.
Sum of Rank-1 outer product
첫 그림과 같은 원리를 활용하여 다음과 같이 활용
선형 독립
- 벡터를 추가할 때마다 span이 증가하게 되면 선형 독립
다음과 같은 모양에서는 영벡터가 유일한 해라면 선형 독립(independence), x 중 하나라도 0이 아닌 해가 존재하면 선형 종속(dependence)이다.
해가 존재하고, 그림과 같이 벡터간의 상관관계가 있다면 해가 무수히 많다.
Subspace, 부분공간
선형 결합에 대해 닫혀있는 벡터공간의 부분 집합이다. -> span과 유사
선형 독립적(중복을 허용하지 않음)
- subspace를 표현할 수 있는 basis(기저)는 유일하지 않다.
- 기저는 모든 재료벡터들이 선형 독립이고 해당 벡터들이 부분공간 전체를 표현 가능한 벡터들의 집합을 의미한다. 기저는 (1, 0, 0) = (2, 0, 0)이므로 둘 중 하나만 있어도 된다. 따라서 기저는 유일하지 않다. 차원은 유일하다.
- Dimension(차원) : subspace의 basis 갯수
선형 종속을 만족하는 경우, 다음과 같은 결과를 볼 수 있다.
- 계수(rank) : 열 공간의 차원 수 = dimension의 갯수 = basis의 갯수
열 공간
행렬의 열 벡터를 선형결합하여 얻어지는 벡터 공간
Transformation, 선형변환
T(cu + cv) = cT(u) + dT(v) 를 만족해야 한다.
Onto, 전사
공역과 치역이 같아지는 경우
공역=치역이 되기 위해선, 정의역이 공역의 갯수보다 크거나 같아야(1대1)한다. 그렇다고 항상 Onto가 되는 것은 아님. 같은 방향의 중복 벡터가 포함되어 있을 수 있기 때문
선형독립이면 1대1, 선형종속이면 1대n
3. Least Square
근사적으로 최대한 해를 구하는 과정
Inner Product, 내적
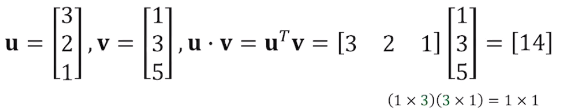
Vector Norm, 길이
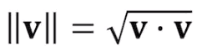
Unit Vector, 단위벡터
길이가 1인 벡터
벡터 사이의 거리
두 벡터 사이의 각
Orthogonal Vector, 직교벡터
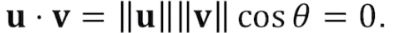
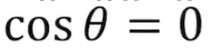
Over Determined System
error는 Sum of Squared errors를 의미
Normal Equation
다음 수식으로 부터
다음을 유도할 수 있다. x hat은 x로 볼 수 있다.
다음 수식이 역행렬을 가져야 성립한다.
Orthogonal Projection
주어진 벡터들이 모두 서로 수직인 관계
수선의 발 yhat의 벡터는 다음과 같이 구할 수 있다. u가 단위 벡터라면 분모는 1이기 때문에 생략해도 된다. *벡터 u는 yhat과 같은 방향의 벡터, span{u}
- span{u1, u2}의 경우
- A = U = span{u1, u2}라고 한다면,
Gram-Schmidt Orthogonalization, 그람-슈미트 직교화

여기서 v1=x1이다. x1을 기준으로 했기 때문.
QR Factorization, QR 분해
A = QR로 분해하는 방법. 복잡...