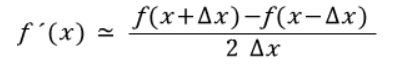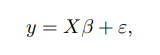1일차
- 드디어 기다리고 기다리던 머신러닝/딥러닝 부분이다.
- 데이터 분석 부분의 경우, 진도가 다 끝난 뒤 복기하는 느낌으로 기록중이지만
- ML/DL부분은 공부하면서 같이 정리해보려고 한다.
AI(Artificial Intellegence)
- 인공지능을 의미하며, 사람의 사고능력을 구현한 시스템(프로그램)이다
- 두가지로 분류할 수 있다.
-> Strong AI : 사람과 구분이 되지 않는 AI
-> Weak AI : 특정한 분야에서 동작하는 AI
ex) Chat GPT
-> AI 연구의 최종 목표는 Strong AI의 구현이라고 볼 수 있다!
구현 방법
- 진화 알고리즘
- 퍼지 조직
- Symbolic AI
- 케이스 기반 추출
- Machine Learning(머신 러닝)
-> 데이터를 기반으로 (스스로) 학습하고 개선하도록 training하는데 중점을 둔 프로그래밍 방식
- 머신러닝은 AI를 구현하는 방법 중 하나!!
머신러닝의 구현 알고리즘
- Regression(회귀)
- SVM(Support Vector Machine)
- Decision Tree(앙상블 -> Random Forest)
- Naive Bayes
- KNN(K-Neurest Neighbors)
- ANN(Artifial Neural Network)
- Clustering(K-Means, DBSCAN)
- Reinforcement Learning(강화학습)
머신러닝의 형태(데이터 형태)
- 지도학습(Supervised Learning)
-> 데이터와 정답이 같이 입력으로 들어가요!
- 비지도학습(Unsupervised Learning)
-> 데이터만 입력으로 들어가요!
- 준지도학습(Semisupervised Learning/지도+비지도)
- 강화학습(Reinforcement Learning)
데이터
- 입력 데이터(x_data,feature,독립변수)
- 출력 데이터(t_data,target,종속변수)
중앙차분법
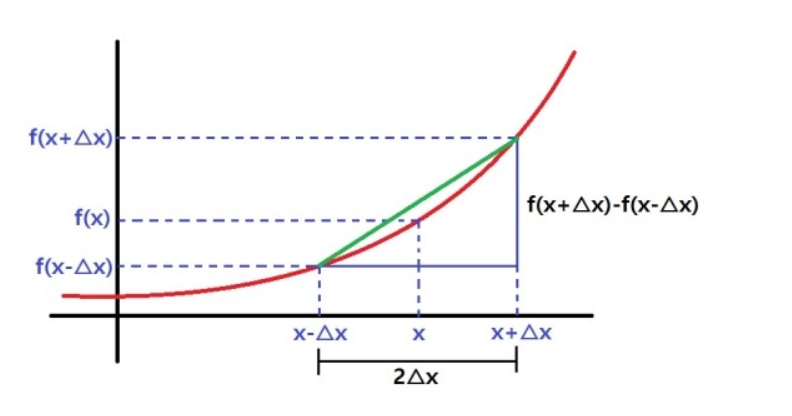
- 위 그림은 중앙차분을 그래프로 나타낸 것이다.
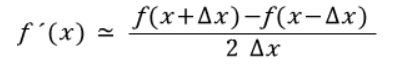
- 중앙차분법의 공식은 위와 같다.
편미분
- 독립변수가 여러 개일때, 미분하고자 하는 변수를 제외하고 나머지 변수를 상수취급해서 미분하는 방법이다
ex) f(x,y) = 2x + 3xy + y^3의 경우에 대해,
x에 대해 편미분하면, 2 + 3y의 값이,
y에 대해 편미분하면 3x + 3y^2의 값이 나온다.
회귀(Regression)
- 어떤 데이터에 대해, 그 데이터에 영향을 주는 조건들의 평균적인 영향력을 이용해 데이터에 대한 조건부 평균을 구하는 기법
->간단히 말하면 평균을 구하는 기법!
회귀를 할 때 알아두어야 할 사항
- 회귀는 기본적으로 평균을 구하는 기법
- 종속변수가 1개인 경우, 단변량 회귀모델
2개 이상인 경우, 다변량 회귀모델
- 많은 회귀모델 중 사용할 모델은 classical linear regression model로, 공식은 아래와 같다
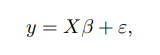
코드 구현
- 개념적인 부분은 위에 있으니 이제 코드로 응용해서 구현해보자!
코드_1(일변수 함수 수치미분)
def numerical_derivative(f, x):
# 입력인자 f는 미분하려는 함수
# 입력인자 x는 미분값을 알고자하는 입력값.
delta_x = 1e-4
# 중앙차분을 이용한 미분을 코드로 표현해보아요!
result = (f(x + delta_x) - f(x - delta_x)) / (2 * delta_x)
return result
# 이 미분함수가 정상적으로 값을 계산하는지 확인해 보아요!
def my_func(x):
return x**2
# 함수 f(x) = x**2의 미분계수 f'(5)를 구해보아요!
result = numerical_derivative(my_func, 5)
print(result) # 9.999999999976694
코드_2(다변수 함수 수치미분)
import numpy as np
def numerical_derivative(f,x):
# f : 미분하려고하는 다변수 함수
# x : 모든 변수를 포함하는 ndarray [1.0 2.0]
# 리턴되는 결과는 [8.0 15.0]
delta_x = 1e-4
derivative_x = np.zeros_like(x) # [0.0 0.0]
it = np.nditer(x, flags=['multi_index'])
while not it.finished:
idx = it.multi_index # 현재의 index를 추출 => tuple형태로 리턴.
tmp = x[idx] # 현재 index의 값을 일단 잠시 보존해야해요!
# 밑에서 이 값을 변경해서 중앙차분 값을 계산해야 해요!
# 그런데 우리 편미분해야해요. 다음 변수 편미분할때
# 원래값으로 복원해야 편미분이 정상적으로 진행되기 때문에
# 이값을 잠시 보관했다가 원상태로 복구해야 해요!
x[idx] = tmp + delta_x
fx_plus_delta_x = f(x) # f(x + delta_x)
x[idx] = tmp - delta_x
fx_minus_delta_x = f(x) # f(x - delta_x)
derivative_x[idx] = (fx_plus_delta_x - fx_minus_delta_x) / (2 * delta_x)
x[idx] = tmp
it.iternext()
return derivative_x
def my_func(x):
return x**2
코드_3
- 위 코드_2의 def my_func을 좀 더 발전시키면 다음과 같다
def my_func(input_data):
x = input_data[0]
y = input_data[1]
# f(x) = 2x + 3xy + y^3
return 2*x + 3*x*y + np.power(y,3)
- np.power(y,3)는 y^3을 계산해주는 넘파이 함수
코드_4
- 이번에는 4변수 함수인 f(w,x,y,z) = wx + xyz + 3w + zy^2를 수치미분 해보자!
def my_func(input_data):
w = input_data[0,0]
x = input_data[0,1]
y = input_data[1,0]
z = input_data[1,1]
return w*x + x*y*z + 3*w + z*np.power(y,2)
data = np.array([[1.0, 2.0],
[3.0, 4.0]])
result = numerical_derivative(my_func, data)
print(result) # [[ 5. 13.], [32. 15.]]
1일차 회고
- 아무래도 평소 잘 쓰지 않는 미분의 개념이 들어오니 코드가 어려워 진 것 같다.
- 개념적으로는 이해가 되도 이를 코드로 구현시키는 과정이 꽤 어려웠었다.