9일차
- 오늘은 어제 배운 비지도 학습의 알고리즘인 K-Means와 DBSCAN에 대해 이어서 진행하겠다
- 두 알고리즘 모두 각각 장단점이 있으니 둘 다 알아두도록 하자!
K-Means
- 동작 원리는 어제 설명했기때문에 간략히 정리하는 느낌으로 가겠다
- 거리 기반의 비지도 알고리즘
- hyperparameter로는 K(클러스터의 개수)가 있다
- EM 알고리즘을 기반으로 동작
- 거리가 멀면서 밀접하게 연관된 data를 성공적으로 군집화하기 힘들다는 단점!
- 속도면에서 장점, 직관적!
DBSCAN
- Density Based Spartial Clustering of Application with Noise
- K-Means 알고리즘의 단점을 보완하기 위해 만들어짐
- K-Means 알고리즘이 거리 기반이였다면 DBSCAN은 밀도 기반
- DBSCAN의 특징
- 클러스터의 개수인 k를 지정할 필요가 없다
- 조밀하게 몰려있는 data로 클러스터를 생성
- 클러스터가 최초의 임의의 점 하나로부터 퍼져나가서 생성된다
- DBSCAN 알고리즘에 나오는 주요 용어
- epsilon : 클러스터의 반경, 클러스터를 구성하는 최소 거리
- minPts : 클러스터를 이루는 최소 개체수
- core point : 클러스터의 중심점
- border point : 클러스터 안에 위치하지만, core가 아닌 점
- noise point : 클러스터 안에 포함되지 못한 data
- 파란색으로 표시한 epsilon, minPts는 hyperparameter로 값을 직접 지정해줘야 한다!
DBSCAN 알고리즘 작동원리
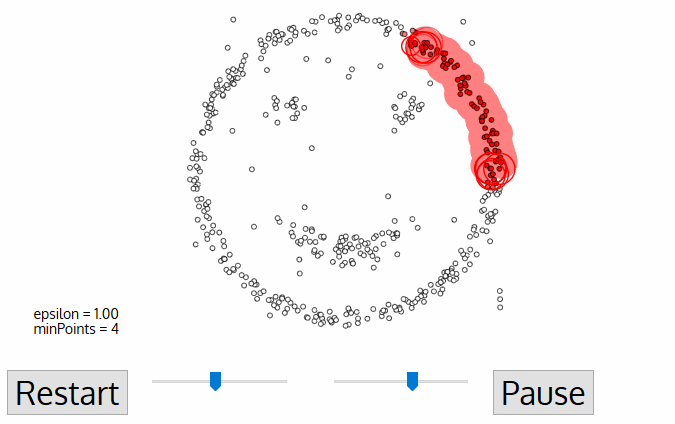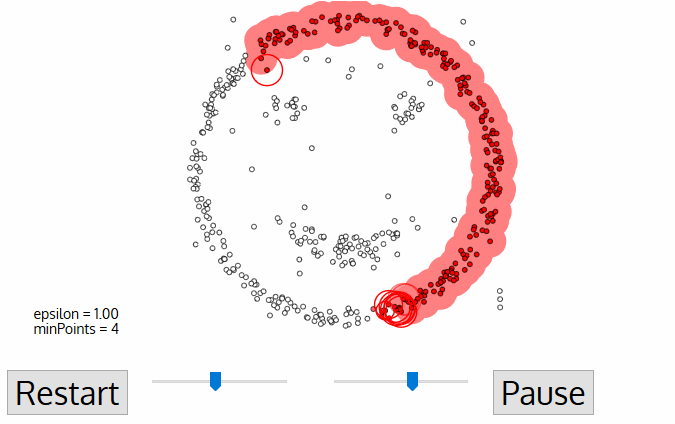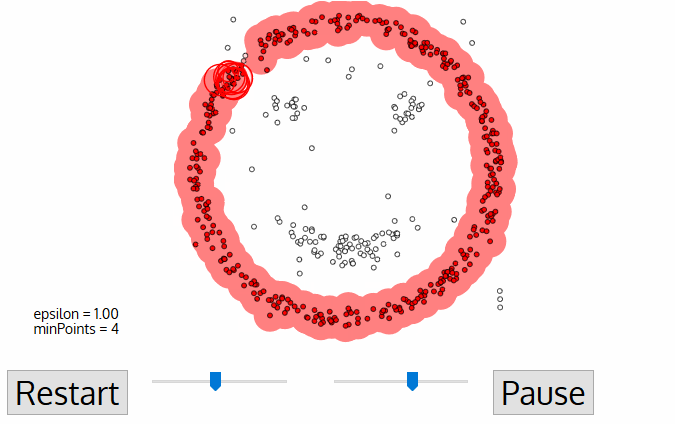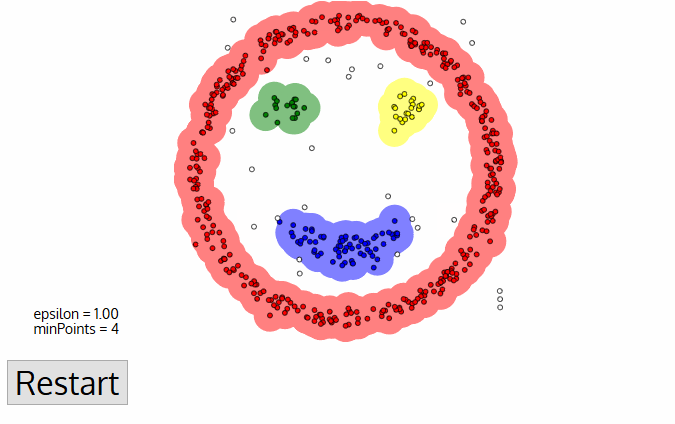
- 임의의 데이터 P를 설정, P를 포함해 epsilon안의 데이터 개수를 센다
- 해당 cluster에 minPts개 이상의 data가 존재하면 P가 core point가 되고 하나의 cluster를 행성
- 새로운 P'가 core point가 되고 이 점이 기존의 cluster에 속하면 하나의 cluster로 묶는다
- 위 과정을 모든 데이터에 대해 반복
- 어느 cluster에도 속하지 않는 데이터는 이상치로 처리
- 데이터가 많아지면 알고리즘의 수행속도가 많이 느려진다는 단점 존재!
차원 축소(Dimension Reduction)
- 쉽게 말해 고차원의 데이터를 저차원으로 변경하는 것
ex) 4차원 -> 2차원 - 저차원 데이터의 표현이 고차원 원본 데이터를 잘 표현할 수 있어야 한다는 전제 필요!
- 차원 축소가 필요한 이유??
- 고차원의 데이터는 상대적으로 데이터 분석도 힘들고 머신러닝 학습도 힘들어 Overfitting 현상이 발생하기 때문
- 시각화 가능, 속도를 높이고 데이터량을 줄일 수 있다는 장점
- 정보 손실(information loss)이 필연적이라는 단점 존재
- 여러가지 알고리즘이 있지만 PCA(주성분 분석)에 대해 알아볼 예정
PCA(주성분 분석)
- 선형 방식의 알고리즘이다
- 쉽게 말해 데이터의 특징을 최대한 살리면서 차원을 축소시키는 방법
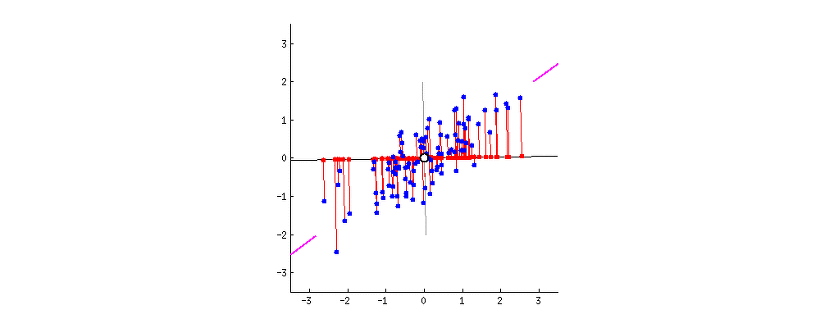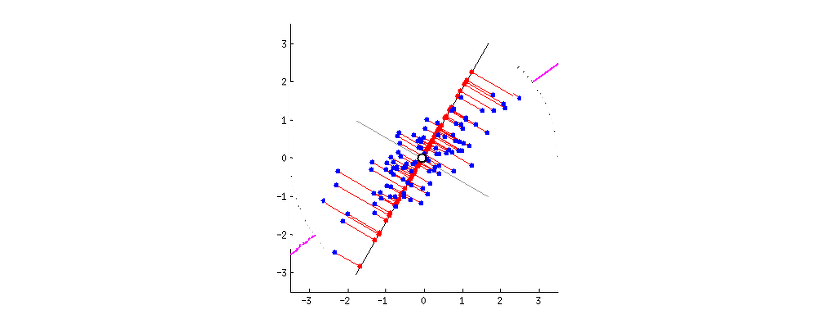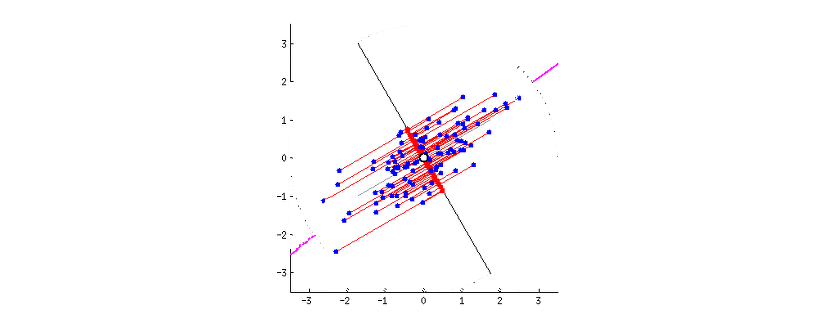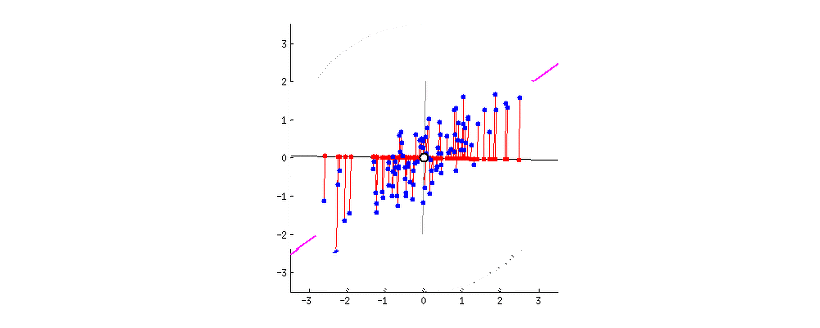
출처: https://excelsior-cjh.tistory.com/167
- pca에 대해 잘 설명해놓은 블로그들로, 여기에서 주성분 분석에 대해 자세히 알 수 있다.
- 내가 설명하는것 보다 잘해놓아서 참고하면 좋을 것 같다
코드 구현
K-Means
# K-Means 비지도 학습을 해보아요!
# 필요 module import
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
# 데이터를 랜덤하게 생성할거에요
# 군집형태로 되어있는 군집데이터 생성할거에요!
# n_samples = 생성할 데이터 개수
# centers = cluster의 개수
# n_features = 쉽게 말하면 데이터의 차원 의미
points,labels = make_blobs(n_samples=100,
centers=4,
n_features=2,
random_state=100)
points.shape
labels.shape
# k-means는 hyperparameter가 k값. 클러스터의 개수.
# n_init : k-means알고리즘을 여러번 실행해 가장 좋은 경우를 선택
# 초기값은 10. 과거에는 이 값을 우리가 설정했는데
# 왠만하면 auto라는 값으로 설정하는게 좋아요!
kmeans_cluster = KMeans(n_clusters=4,
n_init='auto',
random_state=100)
# 모델이 만들어졌으니 이제 학습을 해야 겠죠.
kmeans_cluster.fit(points)
# labels_ : 클러스터값.
print(kmeans_cluster.labels_)
# clustering한 결과를 시각화!
my_color = {0: 'red', 1: 'blue', 2: 'green', 3: 'magenta'}
# 각 cluster마다 scatter를 반복적으로 그리면 되요!
for n in range(4):
cluster_sub_points = points[kmeans_cluster.labels_ == n]
plt.scatter(cluster_sub_points[:,0],
cluster_sub_points[:,1],
color=my_color[n],
label=f'cluster#{n}')
plt.legend()
plt.show()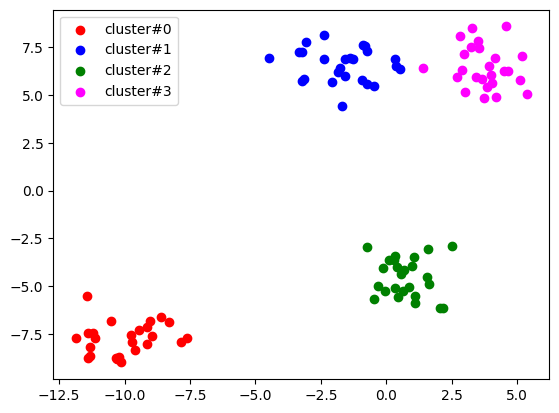
예외
- K-Means 알고리즘이 잘 작동하지 않는 3가지 데이터 예시(원형, 달, 대각선)
- 원형
# 원형으로 되어 있는 데이터를 확보하기 위해 sklearn을 이용
from sklearn.datasets import make_circles
# 이 함수는 두개의 원으로 이루어진 데이터를 생성해요!
# n_samples : 데이터의 총 개수
# factor : 값이 0에 가까울 수록 두 원의 거리가 멀어져요
# 1에 가까울수록 두 원의 거리가 가까워요!
# noise : 데이터에 추가되는 무작위 노이즈의 양
circle_points, circle_labels = make_circles(n_samples=100,
factor=0.5,
noise=0.01)
circle_points.shape # (100, 2)
circle_labels
circle_model = KMeans(n_clusters=2,
n_init='auto')
circle_model.fit(circle_points)
my_color = {0: 'red', 1: 'blue'}
# 각 cluster마다 scatter를 반복적으로 그리면 되요!
for n in range(2):
cluster_sub_points = circle_points[circle_model.labels_ == n]
plt.scatter(cluster_sub_points[:,0],
cluster_sub_points[:,1],
color=my_color[n],
label=f'cluster#{n}')
plt.legend()
plt.show()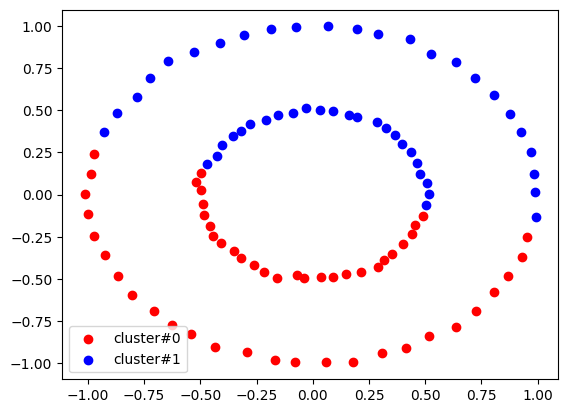
- 달 모양 데이터
from sklearn.datasets import make_moons
moon_points, moon_labels = make_moons(n_samples=100,
noise=0.01)
moon_model = KMeans(n_clusters=2,
n_init='auto')
moon_model.fit(moon_points)
my_color = {0: 'red', 1: 'blue'}
# 각 cluster마다 scatter를 반복적으로 그리면 되요!
for n in range(2):
cluster_sub_points = moon_points[moon_model.labels_ == n]
plt.scatter(cluster_sub_points[:,0],
cluster_sub_points[:,1],
color=my_color[n],
label=f'cluster#{n}')
plt.legend()
plt.show()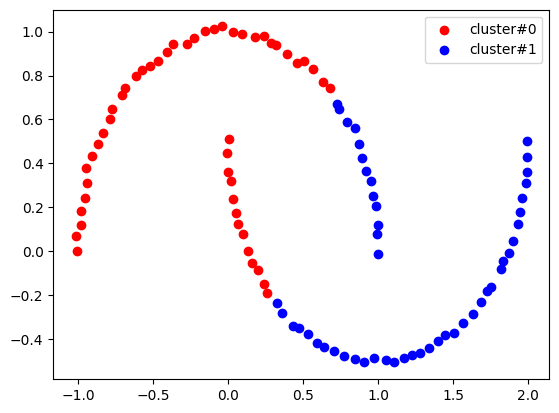
- 대각선 형태
# 세번째 데이터 분포예요!
# 대각선 모양의 데이터에 대해 클러스터링이 잘 되지 않아요!
from sklearn.datasets import make_blobs
diag_points, _ = make_blobs(n_samples=100,
random_state=170)
# 대각행렬을 이용해서 데이터를 대각선 분포로 변형
transfomation = [[0.6, 0.6],
[-0.4, -0.8]]
diag = np.dot(diag_points, transfomation)
diag_model = KMeans(n_clusters=3,
n_init='auto')
diag_model.fit(diag)
my_color = {0: 'red', 1: 'blue', 2: 'green'}
# 각 cluster마다 scatter를 반복적으로 그리면 되요!
for n in range(3):
cluster_sub_points = diag[diag_model.labels_ == n]
plt.scatter(cluster_sub_points[:,0],
cluster_sub_points[:,1],
color=my_color[n],
label=f'cluster#{n}')
plt.legend()
plt.show()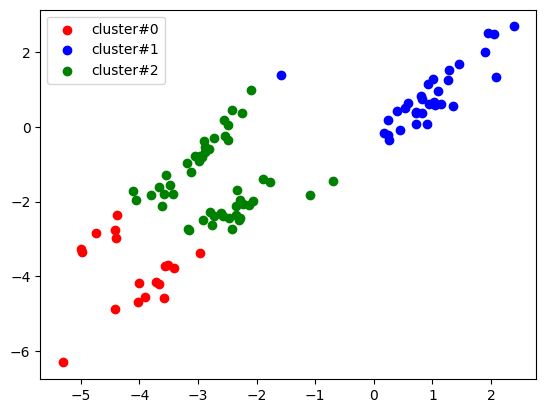
- 위 3가지 데이터 모두 결과가 일반적으로 예상한 것과 다르게 나타난 것을 알 수 있다
- 해결책?? -> DBSCAN!!
DBSCAN
- K-Means가 잘 작동되지 않은 위 3가지의 예시를 DBSCAN으로 실행해보자!
- 원형 데이터
from sklearn.datasets import make_circles
cirlce_points,_ = make_circles(n_samples=100,
factor=0.5,
noise=0.01)
# plt.scatter(circle_points[:,0],circle_points[:,1])
# plt.show()
epsilon=0.2
minPts=3
from sklearn.cluster import DBSCAN
circle_model = DBSCAN(eps=epsilon,
min_samples=minPts)
circle_model.fit(circle_points)
# cluster의 수는 몇개 나오나요?
max(circle_model.labels_)+1
my_color = {0 : 'red', 1 : 'blue'}
for n in range(2):
circle_sub_point = circle_points[circle_model.labels_==n]
plt.scatter(circle_sub_point[:,0],
circle_sub_point[:,1],
color=my_color[n],
label=f'cluster#{n}')
plt.legend()
plt.show()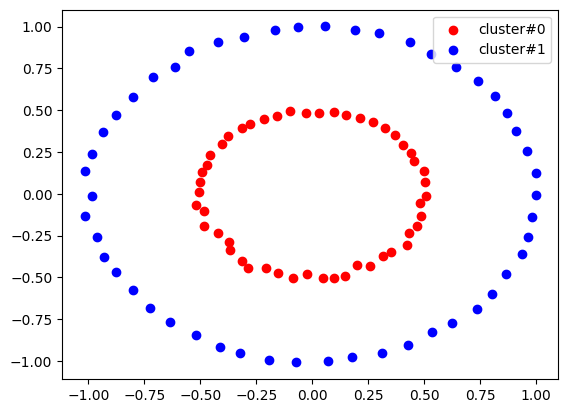
- 달 모양 데이터
from sklearn.datasets import make_moons
moon_points, moon_labels = make_moons(n_samples=100,
noise=0.01)
epsilon=0.2
minPts=3
moon_model = DBSCAN(eps=epsilon,
min_samples=minPts)
moon_model.fit(moon_points)
my_color={0 :'red', 1 : 'blue'}
for n in range(2):
moon_sub_point = moon_points[moon_model.labels_==n]
plt.scatter(moon_sub_point[:,0],
moon_sub_point[:,1],
color=my_color[n],
label=f'cluster#{n}')
plt.legend()
plt.show()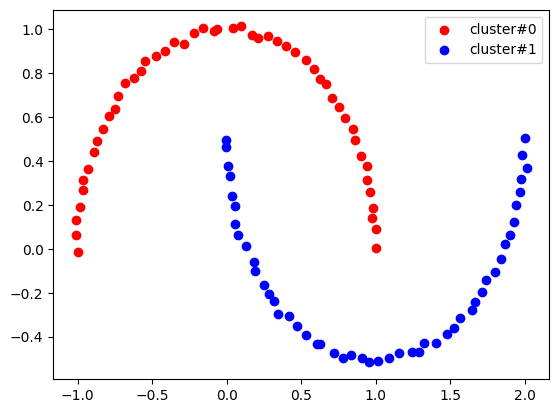
- 대각선 형태 데이터
from sklearn.datasets import make_blobs
from sklearn.cluster import DBSCAN
import numpy as np
diag_points, _ = make_blobs(n_samples=100,
random_state=170)
# 대각 행렬을 이용해서 데이터를 대각선 분포로 변경
transformation = [[0.6,0.6],
[-0.4,-0.8]]
diag_points = np.dot(diag_points, transformation)
# plt.scatter(diag_points[:,0], diag_points[:,1])
# plt.show()
epsilon=0.7
minPts= 3
diag_model = DBSCAN(eps=epsilon,
min_samples=3)
diag_model.fit(diag_points)
my_color ={0 : 'red', 1 : 'blue', 2 : 'green'}
for n in range(3):
cluster_sub_points = diag_points[diag_model.labels_==n]
plt.scatter(cluster_sub_points[:,0],
cluster_sub_points[:,1],
color=my_color[n],
label=f'cluster#{n}')
plt.legend()
plt.show()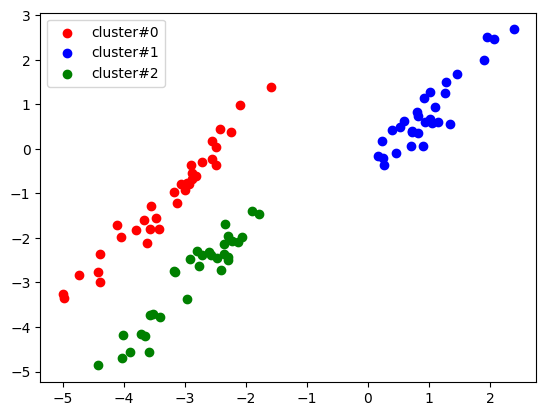
- DBSCAN을 활용하니 K-Means에서는 잘 나오지 않던 결과가 모두 정확히 나오는 것을 알 수 있다!!
차원 축소(PCA)
- iris 데이터를 가지고 차원 축소를 하기 전후 모델의 성능 비교!
- sklearn을 이용해 구현할 예정
- 차원 축소 할 요소 확인
# 차원축소기법 중 주성분분석(PCA)에 대해 알아보아요
# 사용할 예제는 역시나 iris!
# iris는 3가지 품종이 있고 이를 결정짓는 4가지 요소가 있어요!
# 꽃받침(sepal)의 길이와 너비, 꽃잎(petal)의 길이와 너비
# 이 데이터를 차원 축소의 예제로 드는 이유는?
# 독립변수에 대해 상관관계 분석을 해보면 상관관계가 높은 요소 존재
# 이런 경우, 차원축소를 하면 좀 더 좋은 모델을 얻을 수도 있다.
# 필요 module import
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
iris = load_iris()
iris_df = pd.DataFrame(iris.data,
columns=['sepal_height',
'sepal_width',
'petal_height',
'petal_width'])
iris_df
# 상관관계 분석
iris_df.corr()
# feature간에 연관성이 깊어요!
# 따라서 주성분분석(PCA)을 통해 차원을 축소해서 사용하면
# 약간의 데이터 로스가 발생하겠지만 모델의 복잡도가 줄고
# overfitting도 줄어들어서 더 좋은 모델이 만들어 질 수 도 있어요!
# 주성분의 개수를 몇개로 하면 좋을까?
# 주성분의 분산을 사용하면 된다!
from sklearn.decomposition import PCA
pca = PCA(random_state=1004) # 주성분의 개수를 않줬어요!
# 차원을 축소하지는 않아요!
pca.fit_transform(iris_df)
pca.explained_variance_ratio_
# array([0.92461872, 0.05306648, 0.01710261, 0.00521218])- 차원 축소를 활용해 데이터 전처리
# 4개의 독립변수를 차원축소해서 2개의 주성분으로 줄여요!
# 이렇게 데이터를 변환한 다음 다중분류 모델을 만들어서
# 학습하고 정확도를 산출할꺼예요!
# 필요 module import
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# Raw Data Loading
iris = load_iris()
x_data = iris.data
t_data = iris.target
# 결측치와 이상치는 처리하지 않아요
# 정규화 진행
scaler = StandardScaler()
scaler.fit(x_data)
x_data_norm = scaler.transform(x_data)
# PCA를 사용하여 차원 축소를 해보아요!
# 주성분은 2개로 할 예정이에요
n_components = 2
pca = PCA(n_components=n_components)
x_data_norm_pca = pca.fit_transform(x_data_norm)
x_data_norm_pca
# 차원축소도 끝났으니,
# 데이터 분리를 진행해보아요
x_data_train_norm_pca, x_data_test_norm_pca, t_data_train, t_data_test = \
train_test_split(x_data_norm_pca, t_data,
stratify=t_data,
test_size=0.3)- 차원 축소된 데이터 가지고 학습 진행 및 평가
# sklearn 구현
sklearn_model = LogisticRegression()
sklearn_model.fit(x_data_train_norm_pca,
t_data_train)
# 평가를 위해 예측치 생성
predict = sklearn_model.predict(x_data_test_norm_pca)
accuracy = accuracy_score(t_data_test,predict)
accuracy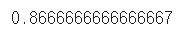
- 차원 축소 하지 않은 ver.
# 차원축소를 하지 않고 정확도 계산해서 비교!
x_data_train_norm, x_data_test_norm, t_data_train_ori, t_data_test_ori = \
train_test_split(x_data_norm,
t_data,
stratify=t_data,
test_size=0.3)
model = LogisticRegression()
model.fit(x_data_train_norm,
t_data_train_ori)
predict = model.predict(x_data_test_norm)
acc = accuracy_score(t_data_test_ori,predict)
acc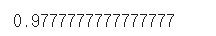
-
차원 축소를 진행하면 데이터 손실이 발생하기때문에 속도는 증가하였으나 정확도는 진행하지 않은 ver.이 더 높은 것을 알 수 있다
-
데이터 전처리는 되어 있으니 tensorflow로도 확인해봅시다!!
-
차원 축소 ver.
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Flatten,Dense
from tensorflow.keras.optimizers import Adam
keras_model = Sequential()
keras_model.add(Flatten(input_shape=(2,)))
keras_model.add(Dense(units=3,
activation='softmax'))
keras_model.compile(optimizer=Adam(learning_rate=1e-1),
loss='sparse_categorical_crossentropy',
metrics=['acc'])
keras_model.fit(x_data_train_norm_pca,
t_data_train,
epochs=100,
verbose=0,
validation_split=0.2)
keras_model.evaluate(x_data_test_norm_pca, t_data_test)
- 차원축소 X ver.
model = Sequential()
model.add(Flatten(input_shape=(4,)))
model.add(Dense(units=3,
activation='softmax'))
model.compile(optimizer=Adam(learning_rate=1e-2),
loss='sparse_categorical_crossentropy',
metrics=['acc'])
model.fit(x_data_train_norm,
t_data_train_ori,
epochs=100,
verbose=0,
validation_split=0.2)
model.evaluate(x_data_test_norm,
t_data_test_ori)
- 수치의 차이는 있지만 결과는 sklearn과 동일한 것을 알 수 있다!!
9일차 회고
- K-Means와 DBSCAN의 경우, 예외 데이터(원형, 달, 대각선)를 통해 비교해보니 그 차이를 확실히 알 수 있었다!
- 차원축소 역시, 익숙한 iris 데이터를 통해 확인했었는데, 어느정도의 데이터 손실이 있다는 것을 알고는 있었지만, 차이가 생각보다 꽤 커서 놀랐다.