📖 학습주제

자료구조/알고리즘 풀기(3)

---

큐(Queue)

자료를 보관할 수 있는 선형 구조
데이터를 넣을 때 한 쪽 끝에서 밀어넣고(enqueue)
꺼낼 때는 반대 쪽에서 깨낸다.(dequeue)
-> 먼저 들어 온 것이 먼저 나온다.(First In First Out)

큐의 연산정의

size() : 큐에 들어있는 원소의 수
isEmpty() : 큐가 비어있는지 확인
enqueue(x) : x를 큐에 추가
dequeue() : 큐 가장 앞에 저장된 원소를 제거 및 반환
peek() : 큐 가장 앞에 저장된 원소를 반환(제거 x)

dequeue() 연산을 제외한 나머지 연산은 O(1)의 시간복잡도를 가진다.
(가장 앞의 원소를 꺼내고 뒤의 원소들이 한칸씩 당겨지기 때문에 dequeue는 O(n)의 시간복잡도를 가진다.)

큐 구현방법

배열 이용

class ArrayQueue:

    def __init__(self):
        self.data = []

    def size(self):
        return len(self.data)

    def isEmpty(self):
        return self.size() == 0

    def enqueue(self, item):
        self.data.append(item)

    def dequeue(self):
        return self.data.pop(0)

    def peek(self):
        return self.data[0]

연결 리스트 이용

class Node:

    def __init__(self, item):
        self.data = item
        self.prev = None
        self.next = None


class DoublyLinkedList:

    def __init__(self):
        self.nodeCount = 0
        self.head = Node(None)
        self.tail = Node(None)
        self.head.prev = None
        self.head.next = self.tail
        self.tail.prev = self.head
        self.tail.next = None


    def __repr__(self):
        if self.nodeCount == 0:
            return 'LinkedList: empty'

        s = ''
        curr = self.head
        while curr.next.next:
            curr = curr.next
            s += repr(curr.data)
            if curr.next.next is not None:
                s += ' -> '
        return s


    def getLength(self):
        return self.nodeCount


    def traverse(self):
        result = []
        curr = self.head
        while curr.next.next:
            curr = curr.next
            result.append(curr.data)
        return result


    def reverse(self):
        result = []
        curr = self.tail
        while curr.prev.prev:
            curr = curr.prev
            result.append(curr.data)
        return result


    def getAt(self, pos):
        if pos < 0 or pos > self.nodeCount:
            return None

        if pos > self.nodeCount // 2:
            i = 0
            curr = self.tail
            while i < self.nodeCount - pos + 1:
                curr = curr.prev
                i += 1
        else:
            i = 0
            curr = self.head
            while i < pos:
                curr = curr.next
                i += 1

        return curr


    def insertAfter(self, prev, newNode):
        next = prev.next
        newNode.prev = prev
        newNode.next = next
        prev.next = newNode
        next.prev = newNode
        self.nodeCount += 1
        return True


    def insertAt(self, pos, newNode):
        if pos < 1 or pos > self.nodeCount + 1:
            return False

        prev = self.getAt(pos - 1)
        return self.insertAfter(prev, newNode)


    def popAfter(self, prev):
        curr = prev.next
        next = curr.next
        prev.next = next
        next.prev = prev
        self.nodeCount -= 1
        return curr.data


    def popAt(self, pos):
        if pos < 1 or pos > self.nodeCount:
            raise IndexError('Index out of range')

        prev = self.getAt(pos - 1)
        return self.popAfter(prev)


    def concat(self, L):
        self.tail.prev.next = L.head.next
        L.head.next.prev = self.tail.prev
        self.tail = L.tail

        self.nodeCount += L.nodeCount


class LinkedListQueue:

    def __init__(self):
        self.data = DoublyLinkedList()

    def size(self):
        return self.data.nodeCount


    def isEmpty(self):
        return self.data.nodeCount == 0


    def enqueue(self, item):
        node = Node(item)
        self.data.insertAt(self.size() + 1, node)

    def dequeue(self):
        return self.data.popAt(1)


    def peek(self):
        return self.data.head.next.data

환형 큐(Circular Queue)

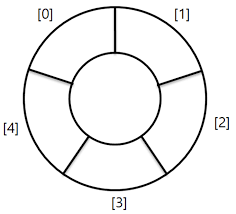
정해진 개수의 저장공간을 돌려가며 이용하는 큐의 형태
-> 큐가 가득차면 더 이상 원소를 넣을 수 없음

rear : 데이터를 집어넣는 포인터
front : 데이터를 꺼내는 포인터

환형 큐의 연산 정의

size() : 큐에 들어있는 원소의 수
isEmpty() : 큐가 비어있는지 확인
isFull() : 큐가 가득 찼는지 확인
enqueue(x) : x를 큐에 추가
dequeue() : 큐 가장 앞에 저장된 원소를 제거 및 반환
peek() : 큐 가장 앞에 저장된 원소를 반환(제거 x)

환형 큐 구현

class CircularQueue:

    def __init__(self, n):
        self.maxCount = n
        self.data = [None] * n
        self.count = 0
        self.front = -1
        self.rear = -1


    def size(self):
        return self.count

    def isEmpty(self):
        return self.count == 0

    def isFull(self):
        return self.count == self.maxCount

    def enqueue(self, x):
        if self.isFull():
            raise IndexError('Queue full')
        self.rear = (self.rear+1)%self.maxCount

        self.data[self.rear] = x
        self.count += 1

    def dequeue(self):
        if self.isEmpty():
            raise IndexError('Queue empty')
        self.front = (self.front+1)%self.maxCount

        x = self.data[self.front]

        self.count -= 1
        return x

    def peek(self):
        if self.isEmpty():
            raise IndexError('Queue empty')
        return self.data[(self.front+1)%self.maxCount]

우선순위 큐(Priority Queue)

큐가 FIFO의 방식을 따르지 않고 우선순위에 따라 원소를 꺼냄

우선순위 큐를 구현하는 방식에는 두 가지가 있다.

• Enqueue 할 때 우선순위를 유지 (더 유리한 방법)
• Dequeue 할 때 우선순위 높은 것을 선택

우선순위 큐의 구현

class Node:

    def __init__(self, item):
        self.data = item
        self.prev = None
        self.next = None


class DoublyLinkedList:

    def __init__(self):
        self.nodeCount = 0
        self.head = Node(None)
        self.tail = Node(None)
        self.head.prev = None
        self.head.next = self.tail
        self.tail.prev = self.head
        self.tail.next = None


    def __repr__(self):
        if self.nodeCount == 0:
            return 'LinkedList: empty'

        s = ''
        curr = self.head
        while curr.next.next:
            curr = curr.next
            s += repr(curr.data)
            if curr.next.next is not None:
                s += ' -> '
        return s


    def getLength(self):
        return self.nodeCount


    def traverse(self):
        result = []
        curr = self.head
        while curr.next.next:
            curr = curr.next
            result.append(curr.data)
        return result


    def reverse(self):
        result = []
        curr = self.tail
        while curr.prev.prev:
            curr = curr.prev
            result.append(curr.data)
        return result


    def getAt(self, pos):
        if pos < 0 or pos > self.nodeCount:
            return None

        if pos > self.nodeCount // 2:
            i = 0
            curr = self.tail
            while i < self.nodeCount - pos + 1:
                curr = curr.prev
                i += 1
        else:
            i = 0
            curr = self.head
            while i < pos:
                curr = curr.next
                i += 1

        return curr


    def insertAfter(self, prev, newNode):
        next = prev.next
        newNode.prev = prev
        newNode.next = next
        prev.next = newNode
        next.prev = newNode
        self.nodeCount += 1
        return True


    def insertAt(self, pos, newNode):
        if pos < 1 or pos > self.nodeCount + 1:
            return False

        prev = self.getAt(pos - 1)
        return self.insertAfter(prev, newNode)


    def popAfter(self, prev):
        curr = prev.next
        next = curr.next
        prev.next = next
        next.prev = prev
        self.nodeCount -= 1
        return curr.data


    def popAt(self, pos):
        if pos < 1 or pos > self.nodeCount:
            return None

        prev = self.getAt(pos - 1)
        return self.popAfter(prev)


    def concat(self, L):
        self.tail.prev.next = L.head.next
        L.head.next.prev = self.tail.prev
        self.tail = L.tail

        self.nodeCount += L.nodeCount


class PriorityQueue:

    def __init__(self):
        self.queue = DoublyLinkedList()


    def size(self):
        return self.queue.getLength()

    def isEmpty(self):
        return self.size() == 0

    def enqueue(self, x):
        newNode = Node(x)
        curr = self.queue.head

        while curr.next.next != None and x < curr.next.data:
            curr = curr.next
        self.queue.insertAfter(curr, newNode)

    def dequeue(self):
        return self.queue.popAt(self.queue.getLength())

    def peek(self):
        return self.queue.getAt(self.queue.getLength()).data

---

트리(Tree)

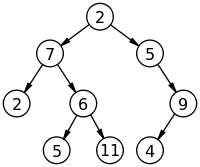
노드(Node)와 엣지(Edge)를 이용해 데이터의 배치 형태를 추상화한 자료구조

• 루트(Root) : 윗 노드(부모 노드)가 없는 가장 위의 노드
• 리프(Leaf) : 아래 노드(자식 노드)가 없는 가장 말단 노드
• 부모 노드 : 엣지로 연결된 노드들 중 루트에 가까운 노드
• 자식 노드 : 엣지로 연결된 노드들 중 리프에 가까운 노드
• 수준(Level) : 각 노드까지 도달하기 위해 필요한 간선의 수
• 형제 노드 : 같은 수준에 있는 노드
• 깊이(depth) : 트리의 최대 수준 + 1
• 서브트리(SubTree) : 특정 노드 아래의 모든 후손노드를 포함하는 트리
• 차수(Degree) : 자식노드의 수 (0이면 리프)

이진 트리(Binary Tree)

모든 노드의 차수가 2 이하인 트리구조

• 포화 이진 트리(Full Binary Tree)
  모든 수준에서 노드들이 모두 채워져있는 이진 트리의 구조(깊이 n일 떄 노드의 개수가 2ⁿ- 1)

• 완전 이진 트리(Complete Binary Tree)
  깊이 k인 완전 이진 트리에 대해 k-2수준까지는 포화 이진 트리, k-1수준에서는 왼쪽에서부터 순차적으로 채워진 구조

이진 트리의 연산 정의

size() : 노드의 갯수
전체 이진 트리의 size = 왼쪽 서브트리의 size + 오른쪽 서브트리의 size + 1
depth() : 트리의 깊이
전체 이진 트리의 depth = max(왼쪽 서브트리의 depth, 오른쪽 서브트리의 depth) + 1

이진 트리의 구현

class Node:

    def __init__(self, item):
        self.data = item
        self.left = None
        self.right = None


    def size(self):
        l = self.left.size() if self.left else 0
        r = self.right.size() if self.right else 0
        return l + r + 1


    def depth(self):
        l = self.left.depth() if self.left else 0
        r = self.right.depth() if self.right else 0
        return max(l, r)+1
        


class BinaryTree:

    def __init__(self, r):
        self.root = r

    def size(self):
        if self.root:
            return self.root.size()
        else:
            return 0


    def depth(self):
        if self.root:
            return self.root.depth()
        else:
            return 0

이진 트리의 순회

깊이 우선 탐색(Depth First Search)

• 중위 순회(In-order Traverse)
  순회 순서 : 왼쪽 서브트리 -> 자기자신 -> 오른쪽 서브트리
  
  
• 전위 순회(Pre-order Traverse)
  순회 순서 : 자기자신 -> 왼쪽 서브트리 -> 오른쪽 서브트리
  
  
• 후위 순회(Post order Traverse)
  순회 순서 : 왼쪽 서브트리 -> 오른쪽 서브트리 -> 자기자신

너비 우선 탐색(Breadth First Search)

수준이 높은 노드를 우선으로 탐색
한 노드를 탐색했을 때 나중에 방문할 노드들의 순서도 기록해야 한다.
-> 큐 사용

순회 구현

class Node:

    def __init__(self, item):
        self.data = item
        self.left = None
        self.right = None


    def inorder(self):
        traversal = []
        if self.left:
            traversal += self.left.inorder()
        traversal.append(self.data)
        if self.right:
            traversal += self.right.inorder()
        return traversal


    def preorder(self):
        traversal = []
        traversal.append(self.data)
        if self.left:
            traversal += self.left.preorder()
        if self.right:
            traversal += self.right.preorder()
        return traversal
        
    def postorder(self):
        traversal = []
        if self.left:
            traversal += self.left.postorder()
        if self.right:
            traversal += self.right.postorder()
        traversal.append(self.data)
        return traversal
            


class BinaryTree:

    def __init__(self, r):
        self.root = r


    def inorder(self):
        if self.root:
            return self.root.inorder()
        else:
            return []


    def preorder(self):
        if self.root:
            return self.root.preorder()
        else:
            return []
            
    def postorder(self):
        if self.root:
            return self.root.postorder()
        else:
            return []

이진 탐색 트리(Binary Search Tree)

모든 노드에 대해 왼쪽 서브 트리는 현재 노드보다 작고 오른쪽 서브 트리는 현재 노드보다 큰 구조를 가지고 있다.

이진탐색법과의 비교

이진탐색법에 비해 데이터 원소의 추가, 삭제가 용이하나 공간 소모가 큼

이진 탐색 트리의 연산 정의

insert(key, data) : 트리에 주어진 데이터 원소 추가
remove(key) : 트리에서 특정 원소 삭제
lookup(key) : 특정 원소 검색
inorder() : 키의 순서에 떄라 데이터 원소 나열
min(),max() : 각각 최소, 최대키를 가지는 원소 탐색

이진 탐색 트리의 구현

class Node:

    def __init__(self, key, data):
        self.key = key
        self.data = data
        self.left = None
        self.right = None


    def insert(self, key, data):
        if key < self.key:
            if self.left:
                self.left.insert(key, data)
            else:
                self.left = Node(key, data)
            
        elif key > self.key:
            if self.right:
                self.right.insert(key, data)
                
            else:
                self.right = Node(key, data)
        
        else:
            raise KeyError('ValueError')
                
        return True


    def inorder(self):
        traversal = []
        if self.left:
            traversal += self.left.inorder()
        traversal.append(self)
        if self.right:
            traversal += self.right.inorder()
        return traversal
    
    def countChildren(self):
        count = 0
        if self.left:
            count += 1
        if self.right:
            count += 1
        return count


class BinSearchTree:

    def __init__(self):
        self.root = None


    def insert(self, key, data):
        if self.root:
            self.root.insert(key, data)
        else:
            self.root = Node(key, data)


    def remove(self, key):
        node, parent = self.lookup(key)
        
        if node:
            nChildren = node.countChildren()

            if nChildren == 0:
                # 만약 parent 가 있으면
                # node 가 왼쪽 자식인지 오른쪽 자식인지 판단하여
                # parent.left 또는 parent.right 를 None 으로 하여
                # leaf node 였던 자식을 트리에서 끊어내어 없앱니다.
                if parent:
                    if node == parent.left:
                        parent.left = None
                    if node == parent.right:
                        parent.right = None
                # 만약 parent 가 없으면 (node 는 root 인 경우)
                # self.root 를 None 으로 하여 빈 트리로 만듭니다.
                else:
                    self.root = None
            # When the node has only one child
            elif nChildren == 1:
                # 하나 있는 자식이 왼쪽인지 오른쪽인지를 판단하여
                # 그 자식을 어떤 변수가 가리키도록 합니다.
                if node.left:
                    direction = node.left
                else:
                    direction = node.right
                # 만약 parent 가 있으면
                # node 가 왼쪽 자식인지 오른쪽 자식인지 판단하여
                # 위에서 가리킨 자식을 대신 node 의 자리에 넣습니다.
                if parent:
                    if node == parent.left:
                        parent.left = direction
                    else:
                        parent.right = direction
                # 만약 parent 가 없으면 (node 는 root 인 경우)
                # self.root 에 위에서 가리킨 자식을 대신 넣습니다.
                else:
                    self.root = direction
            # When the node has both left and right children
            else:
                parent = node
                successor = node.right
                # parent 는 node 를 가리키고 있고,
                # successor 는 node 의 오른쪽 자식을 가리키고 있으므로
                # successor 로부터 왼쪽 자식의 링크를 반복하여 따라감으로써
                # 순환문이 종료할 때 successor 는 바로 다음 키를 가진 노드를,
                # 그리고 parent 는 그 노드의 부모 노드를 가리키도록 찾아냅니다.
                while successor.left:
                    parent = successor
                    successor = successor.left
                # 삭제하려는 노드인 node 에 successor 의 key 와 data 를 대입합니다.
                node.key = successor.key
                node.data = successor.data
                # 이제, successor 가 parent 의 왼쪽 자식인지 오른쪽 자식인지를 판단하여
                # 그에 따라 parent.left 또는 parent.right 를
                # successor 가 가지고 있던 (없을 수도 있지만) 자식을 가리키도록 합니다.
                if successor.key is parent.left.key:
                    parent.left = successor.right
                else:
                    parent.right = successor.right

            return True

        else:
            return False
            
    def inorder(self):
        if self.root:
            return self.root.inorder()
        else:
            return []

---

힙(Heap)

다음 조건을 만족시키는 이진트리

• 언제나 부모가 자식보다 크거나 같다.(루트가 언제나 최대(MaxHeap) 혹은 최소(MinHeap))
• 완전 이진트리