📖 학습주제

머신러닝, Scikit-learn, 실전 머신러닝 문제 실습 (2)

---

머신러닝을 위한 기초 선형대수

선형대수를 알아야 하는 이유

Deep learning을 이해하기 위해서 반드시 선형대수 + 행렬미분 + 확률의 탄탄한 기초가 필요하다.
Transformer의 attention matrix의 예를 보자.

이렇게 핵심 아이디어가 행렬에 관한 식으로 표현되는 경우가 많다.

기본 표기법 (Basic Notation)

• $A \in \mathbb{R}^{m \times n}$는 $m$개의 행과 $n$개의 열을 가진 행렬을 의미
• $x \in \mathbb{R}^{n}$는 $n$개의 원소를 가진 벡터를 의미
  - $n$개의 행과 1개의 열을 가진 행렬로 생각할 수 있다.
  - 열벡터(column vector)라고 부르기도 함(명시적으로 행벡터(row vector)를 표현하고자 한다면 $x^T$로 씀, $T$는 transpose)
• 벡터 $x$의 $i$번째 원소를 $x_i$로 표기
  $x = \begin{bmatrix}x_1\\x_2\\\vdots\\x_i\\\vdots\\x_n \end{bmatrix}$
• $a_{ij}$ (또는 $A_{ij}, A_{i,j}$)는 행렬 $A$의 $i$번째 행, $j$번째 열의 원소를 의미
  $A = \begin{bmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{m1}&a_{m2}&\cdots&a_{mn} \end{bmatrix}$
• 행렬$A$의 $j$번째 열을 $a_j$(또는 $A_{\cdot j}$), $i$번째 행을 $a_{i}^{T}$(또는 $A_{i \cdot}^T$)로 표기

In Python

• numpy(이하 np)의 array를 이용해 배열을 생성할 수 있다.
• np.expand_dims(arr, axis) : 배열의 차원을 확장
• arr.shape : 배열의 형태
• arr[:, j] : 열벡터, arr[i, :] : 행벡터

행렬의 곱셉 (Matrix Multiplication)

행렬 $A \in \mathbb{R}^{m \times n}$, $B \in \mathbb{R}^{n \times p}$에 대해, 두 행렬의 곱 $C \in \mathbb{R}^{m \times p}$는 다음과 같이 정의된다.

벡터 $\times$ 벡터 (Vector-Vector Products)

벡터 $x,y \in \mathbb{R}^{n}$에 대해, 두 벡터의 내적(inner product) $x^Ty$는 다음과 같이 정의된다.

벡터 $x \in \mathbb{R}^{m}, y \in \mathbb{R}^{n}$에 대해, 두 벡터의 외적(outer product) $xy^T$는 다음과 같이 정의된다.

행렬 $\times$ 벡터 (Matrix-Vector Products)

행렬 $A \in \mathbb{R}^{m \times n}$와 벡터 $x \in \mathbb{R}^{n}$에 대해, 각 행렬과 벡터의 곱 $y$는 $y = Ax \in \mathbb{R}^m$으로 정의된다.

In Python

• arr1.dot(arr2) : arr1과 arr2의 내적
• np.matmul(arr1, arr2) : arr1과 arr2의 행렬곱

중요 연산과 성질들 (Operations and Properties)

• 정방행렬(square matrix) : 행과 열의 개수가 동일
• 상삼각행렬(upper triangular matrix) : 정방행렬이며 대각선 원소 아래 원소들이 모두 0
• 하삼각행렬(lower triangular matrix) : 정방행렬이며 대각선 원소 위 원소들이 모두 0
• 대각행렬(diagonal matrix) : 정방행렬이며 대각선 원소를 제외한 모든 원소가 0
• 단위행렬(identity matrix): 대각행렬이며 대각선 원소들이 모두 1. $I$로 표시

In Python

• np.diag(arr) : 대각행렬을 리턴
• np.eye(n) : 크기 n의 단위행렬을 리턴

전치 (Transpose)

행렬 $A \in \mathbb{R}^{m \times n}$에 대해, 그 행렬의 전치행렬을 $A^T \in \mathbb{R}^{n \times m}$으로 표기하고 다음과 같이 정의한다.

전치의 성질

• $(A^T)^T = A$
• $(AB)^T = B^TA^T$
• $(A+B)^T = A^T+B^T$

In Python

• arr.T : 전치행렬을 리턴

대칭행렬 (Symmetic Matrices)

정방행렬 $A \in \mathbb{R}^{n \times n}$과 그 행렬의 전치행렬 $A^T \in \mathbb{R}^{n \times n}$에 대해,
$A=A^T$이면 $A$를 대칭행렬이라고 하고 $A=-A^T$이면 반대칭행렬이라고 한다.

대칭행렬의 성질

• $AA^T$는 항상 대칭
• $A+A^T$는 대칭, $A-A^T$는 반대칭

대각합(Trace)

정방행렬 $A \in \mathbb{R}^{n \times n}$에 대해, $\displaystyle\sum_{i=1}^{n}A_{ii}$를 $A$의 대각합이라고 하고 $tr(A)$로 표기한다.

대각합의 성질

$A \in \mathbb{R}^{n \times n}, B \in \mathbb{R}^{n \times n}, t \in \mathbb{R}$에 대해,

• $tr(A) = tr(A^T)$
• $tr(A+B)=tr(A)+tr(B)$
• $tr(tA) = t\cdot tr(A)$

행렬곱($AB\,or\, ABC$)이 정방행렬이 되는 $A,B,C$에 대해

• $tr(AB)=tr(BA)$
• $tr(ABC)=tr(BCA)=tr(CAB)$

norm

벡터공간에서 벡터의 길이, 크기, 거리 등을 나타낼 때 사용되며, $l_2(Euclidean\; norm)$은 다음과 같이 정의된다.

$l_p(Frobenius\;norm)$

$Frobenius\;norm$에 대해

In Python

numpy.linalg(이하 LA)를 import

• LA.norm(arr) : norm값 리턴

선형독립

벡터들의 집합 $X = \lbrace x_1,x_2,\cdots,x_n \rbrace \subset \mathbb{R}^n$에 대해, 모든 $X$의 원소가 다른 원소들의 선형 결합으로 나타낼 수 없을 때 이를 선형독립(Linear Independent)이라고 한다. (반대는 선형 종속(Linear dependent))

Rank

• Column rank : 행렬 $A \in \mathbb{R}^{m \times n}$의 열들의 부분집합 중에서 가장 큰 선형독립인 집합의 크기
• Row rank : 행렬 $A \in \mathbb{R}^{m \times n}$의 행들의 부분집합 중에서 가장 큰 선형독립인 집합의 크기
• 모든 행렬의 column rank와 row rank는 동일하며 행렬 $A$의 랭크를 $rank(A)$로 표시한다.

Rank의 성질

행렬 $A \in \mathbb{R}^{m \times n}$, $B \in \mathbb{R}^{n \times p}$에 대해

• $rank(A) \leq min(m,n)$
• $rank(A) = min(m,n)$일 때, $A$가 $full\; rank$라고 한다.
• $rank(A) = rank(A^T)$
• $rank(AB) \leq min(rank(A),rank(B))$
• $rank(A+B) \leq rank(A)+rank(B)$, (단, $A,B \in \mathbb{R}^{m \times n}$)

In Python

• LA.matrix_rank(A) : rank를 리턴

역행렬(Inverse matrix)

정방행렬 $A \in \mathbb{R}^{n \times n}$에 대해, $AA^{-1}=I=A^{-1}A$일 때, $A^{-1}$를 $A$의 역행렬이라고 하며 이 때, $A$를 $invertible$(또는 $non-singular$)하다고 한다.

역행렬의 성질

• $A\; is\; invertible \Leftrightarrow A\; is\; full\;rank$
• $(A^{-1})^{-1} = A$
• $(AB)^{-1}=B^{-1}A^{-1}$
• $(A^T)^{-1}=(A^{-1})^T$

In Python

• LA.inv(A) : 역행렬을 리턴

직교행렬 (Orthogonal Matrices)

두 벡터 $x, y \in \mathbb{R}^n$에 대해 $x^Ty=0$ 일 때, 두 벡터가 직교(Orthogonal)한다고 하며 모든 열들이 서로 직교이고 정규화된 정방행렬 $U\in \mathbb{R}^{n\times n}$를 직교행렬이라고 한다. 또한, $\|x\|_2 = 1$인 벡터 $x\in \mathbb{R}^n$를 정규화(normalized)된 벡터라고 한다.

직교행렬의 성질

• $U^TU = I$
• $UU^T = I$
• $U^{-1} = U^T$
• $\|Ux\|_2 = \|x\|_2$ for any $x\in \mathbb{R}^{n}$
  • $\|Ux\|_2 = \big((Ux)^T(Ux)\big)^{1/2} = \big(x^TU^TUx\big)^{1/2} = (x^Tx)^{1/2} = \|x\|_2$

치역(Range), 영공간(Nullspace)

생성집합(Span)

벡터의 집합 $X = \{x_1,x_2,\ldots,x_n\}$에 대해,
$Y=\left\{ v : v = \sum_{i=1}^n\alpha_i x_i, \alpha_i \in \mathbb{R} \right\}$를 $X$의 생성집합($Span$)이라고 하고 $\mathrm{span}(X)$로 표기한다.

치역 (range)

행렬 $A\in \mathbb{R}^{m\times n}$에 대해, $A$의 모든 열들에 대한 생성($span$)을 치역이라고 하며 $\mathcal{R}(A)$로 표기한다.

영공간 (nullspace)

행렬 $A\in \mathbb{R}^{m\times n}$에 대해, $A$와 곱해졌을 때 0이 되는 모든 벡터들의 집합을 영공간이라고 하며 $\mathcal{N}(A)$로 표기한다.

치역, 영공간에 대한 성질

• $\{w : w = u + v, u\in \mathcal{R}(A^T), v \in \mathcal{N}(A)\} = \mathbb{R}^n ~\mathrm{and}~ \mathcal{R}(A^T) \cap \mathcal{N}(A) = \{0\}$

직교여공간(orthogonal complements)

$\mathcal{R}(A^T)$와 $\mathcal{N}(A)$를 직교여공간(orthogonal complements)라고 하며 $\mathcal{R}(A^T) = \mathcal{N}(A)^\perp$라고 표시한다.

사영 (projection)

$A$의 치역 $\mathcal{R}(A)$, 벡터 $y\in \mathbb{R}^m$에 대해, 다음을 만족할 때 $\mathrm{Proj}(y;A)$를 $\mathcal{R}(A)$ 위로 벡터 $y$의 사영(projection)이라고 한다.

$U^TU = I$인 정방행렬 $U$는 $UU^T = I$임을 증명

• $U$의 치역은 전체공간이므로 임의의 $y$에 대해 $\mathrm{Proj}(y;U) = y$이어야 한다.
• 모든 $y$에 대해 $U(U^TU)^{-1}Uy = y$이어야 하므로 $U(U^TU)^{-1}U^T= I$이다.
• 따라서 $UU^T = I$이다.

행렬식 (Determinant)

정방행렬 $A\in \mathbb{R}^{n\times n}$의 행렬식(determinant) $|A|$ (또는 $\det (A)$)는 다음과 같이 계산할 수 있다.

$|A| = A_{1,1}\times|A_{\backslash1,\backslash1}| - A_{1,2}\times|A_{\backslash1,\backslash2}| + A_{1,3}\times|A_{\backslash1,\backslash3}| - A_{1,4}\times|A_{\backslash1,\backslash4}| + \cdots ± A_{1,n}\times|A_{\backslash1,\backslash n}|$

여기서 $A_{\backslash i,\backslash j}$는 $i$번째 행과 $j$번째 열을 없애버린 행렬을 의미한다.

e.g.)

$A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 0 \end{bmatrix}$

위의 식을 사용하면 아래와 같이 전개된다.

$|A| = 1 \times \left | \begin{bmatrix} 5 & 6 \\ 8 & 0 \end{bmatrix} \right | - 2 \times \left | \begin{bmatrix} 4 & 6 \\ 7 & 0 \end{bmatrix} \right | + 3 \times \left | \begin{bmatrix} 4 & 5 \\ 7 & 8 \end{bmatrix} \right |$

이제 위의 $2 \times 2$ 행렬들의 행렬식을 계산한다.

$\left | \begin{bmatrix} 5 & 6 \\ 8 & 0 \end{bmatrix} \right | = 5 \times 0 - 6 \times 8 = -48$

$\left | \begin{bmatrix} 4 & 6 \\ 7 & 0 \end{bmatrix} \right | = 4 \times 0 - 6 \times 7 = -42$

$\left | \begin{bmatrix} 4 & 5 \\ 7 & 8 \end{bmatrix} \right | = 4 \times 8 - 5 \times 7 = -3$

따라서,

$|A| = 1 \times (-48) - 2 \times (-42) + 3 \times (-3) = 27$

#### 행렬식의 기하학적 해석

행렬

이 주어졌을 때, 행 벡터들의 선형결합(단 결합에 쓰이는 계수들은 0에서 1사이)이 나타내는 $\mathbb{R}^n$ 공간 상의 모든 점들의 집합 $S$를 생각해보자. 엄밀하게 나타내자면
$S = \{v\in \mathbb{R}^n : v=\sum_{i=1}^n \alpha_i a_i ~\mathrm{where}~ 0\leq \alpha_i \leq 1, i=1,\ldots,n\}$

중요한 사실은 행렬식의 절대값이 이 $S$의 부피(volume)과 일치한다는 것이다!

예를 들어, 행렬

의 행벡터들은

이다. $S$에 속한 점들을 2차원평면에 나타내면 다음과 같다.

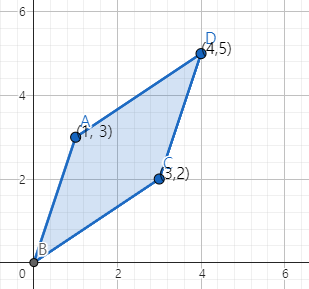
평행사변형 $S$의 넓이는 7인데 이 값은 $A$의 행렬식 $|A|=-7$의 절대값과 일치함을 알 수 있다.

행렬식의 성질

• $|I|=1$
• $A$의 하나의 행에 $t\in \mathbb{R}$를 곱했을 때, 행렬식은 $t|A|$
• $A$의 두 행들을 교환했을 때 행렬식은 $-|A|$
• $A, B\in \mathbb{R}^{n\times n}$에 대해,
  - $|A| = |A^T|$
  - $|AB| = |A| |B|$
  - $|A|=0 \Leftrightarrow A\; is\; not\; invertible$
  - $A$가 $non-singular$할 때, $|A^{-1}| = 1/|A|$.

In Python

• LA.det(A) : 행렬식 값을 리턴

이차형식 (Quadratic Forms)

정방행렬 $A\in \mathbb{R}^{n\times n}$와 벡터 $x\in \mathbb{R}^n$가 주어졌을 때, $scalar$값 $x^TAx$를 이차형식(quadratic form)이라고 하며 다음과 같이 표현할 수 있다.

다음이 성립함을 알 수 있다.

$x^TAx = (x^TAx)^T = x^TA^Tx = x^T\left(\frac{1}{2}A + \frac{1}{2}A^T\right)x$

따라서 이차형식에 나타나는 행렬을 대칭행렬로 가정하는 경우가 많다.

양/음의 (준)정부호

• 대칭행렬 $A\in \mathbb{S}^n$이 0이 아닌 모든 벡터 $x\in \mathbb{R}^n$에 대해서 $x^TAx \gt 0$을 만족할 때, 양의 정부호($positive\; definite$)라고 하고 $A\succ 0$(또는 단순히 $A \gt 0$)로 표시한다. 모든 양의 정부호 행렬들의 집합을 $\mathbb{S}_{++}^n$으로 표시한다.

• 대칭행렬 $A\in \mathbb{S}^n$이 0이 아닌 모든 벡터 $x\in \mathbb{R}^n$에 대해서 $x^TAx \ge 0$을 만족할 때, 양의 준정부호($positive\; semi-definite$)라고 하고 $A\succeq 0$(또는 단순히 $A \ge 0$)로 표시한다. 모든 양의 준정부호 행렬들의 집합을 $\mathbb{S}_{+}^n$으로 표시한다.

• 대칭행렬 $A\in \mathbb{S}^n$이 0이 아닌 모든 벡터 $x\in \mathbb{R}^n$에 대해서 $x^TAx \lt 0$을 만족할 때, 음의 정부호($negative\; definite$)라고 하고 $A\prec 0$(또는 단순히 $A \lt 0$)로 표시한다.

• 대칭행렬 $A\in \mathbb{S}^n$이 0이 아닌 모든 벡터 $x\in \mathbb{R}^n$에 대해서 $x^TAx \leq 0$을 만족할 때, 음의 준정부호($negative\; semi-definite$)라고 하고 $A\preceq 0$(또는 단순히 $A \leq 0$)로 표시한다.

• 대칭행렬 $A\in \mathbb{S}^n$가 양의 준정부호 또는 음의 준정부호도 아닌 경우, 부정부호($indefinite$)라고 한다. 이것은 $x_1^TAx_1 > 0, x_2^TAx_2 < 0$을 만족하는 $x_1, x_2\in \mathbb{R}^n$이 존재한다는 것을 의미한다.

$positive\; definite$ 그리고 $negative\; definite$ 행렬은 $full\; rank$이며 따라서 $invertible$이다.

Gram matrix

임의의 행렬 $A\in \mathbb{R}^{m\times n}$이 주어졌을 때 행렬 $G = A^TA$를 $Gram\; matrix$라고 부르고 항상 ($positive\; semi-definite$이다. 만약 $m\ge n$이고 $A$가 $full\; rank$이면, $G$는 $positive\; definite$이다.

고유값 (Eigen values), 고유벡터 (Eige nvectors)

정방행렬 $A\in \mathbb{R}^{n\times n}$이 주어졌을 때, $Ax = \lambda x, x\neq 0$을 만족하는 $\lambda \in \mathbb{C}$를 $A$의 고유값($eigen\;value$) 그리고 $x\in \mathbb{C}^n$을 연관된 고유벡터($eigen\;vector$)라고 한다.

In Python

• LA.eig(A) : 고유값, 고유벡터 리턴

고유값, 고유벡터의 성질

• $\mathrm{tr}A = \displaystyle\sum_{i=1}^n \lambda_i$
• $|A| = \displaystyle\prod_{i=1}^n \lambda_i$
• $\mathrm{rank}(A)$는 0이 아닌 $A$의 고유값의 개수와 같다.
• $A$가 $non-singular$일 때, $1/\lambda_i$는 $A^{-1}$의 고유값이다(고유벡터 $x_i$와 연관된). 즉, $A^{-1}x_i = (1/\lambda_i)x_i$이다.
• 대각행렬 $D = \mathrm{diag}(d_1,\ldots,d_n)$의 고유값들은 $d_1,\ldots,d_n$이다.

행렬미분 (Matrix Calculus)

Gradient

행렬 $A\in \mathbb{R}^{m\times n}$를 입력으로 받아서 실수값을 돌려주는 함수 $f : \mathbb{R}^{m\times n} \to \mathbb{R}$이 있다고 하자. $f$의 $gradient$는 다음과 같이 정의된다.

$(\nabla_Af(A))_{ij} = \frac{\partial f(A)}{\partial A_{ij}}$

특별히 $A$가 벡터 $x\in \mathbb{R}^n$인 경우는,

Hessian

$(\nabla_x^2 f(x))_{ij} = \frac{\partial^2 f(x)}{\partial x_i \partial x_j}$

중요한 공식

$x, b\in \mathbb{R}^n$, $A\in \mathbb{S}^n$일 때 다음이 성립한다.

• $\nabla_x b^Tx = b$
• $\nabla_x x^TAx = 2Ax$
• $\nabla_x^2 x^TAx = 2A$
• $\nabla_A \log |A| = A^{-1}$ ($A\in\mathbb{S}_{++}^n$인 경우)

벡터가 아닌 경우

• $(bx)' = b$
• $(ax^2)' = 2ax$
• $(\log x)' = x^{-1}$