모노톤 스택, 큐,덱에 관하여.

서론.

while (!stack.isEmpty() && 자료[stack.peek()] < 자료[i])

스택, 큐, 덱 문제들을 푸는 동안 많은 알고리즘들이 해당 알고리즘을 사용하는 것을 보았다

하나같이 해당 형식을 따르고 있는 것을 보고 뭔가 정형화된 알고리즘이 있나? 생각이 들었는데 스터디를 하면서 해당 알고리즘을 모노톤 스택, 큐, 덱 이라고 한다는 것을 알고 정리해보고자 한다.

monotonic 이란?

영어를 잘 못하는 필자이기에 뜻부터 찾아봤다.

단조롭다라는 뜻이란다 뭐가 단조롭다는 뜻일까?

변수와 결괏값이 단조롭다는 뜻이다.

변수와 결괏값이 증가할때는 함께 증가하고 감소할땐 함께 감소한다. 그렇다면 단조로운 거다.

사실 여기에 쓰인 monotonic은 통계 용어인 Monotonic Relationship에서 사용된 단어이다.

해당 단어는 값이 증가/감소할 때 때 다른 값들도 같은 방향으로 증가/감소 관계를 뜻한다.

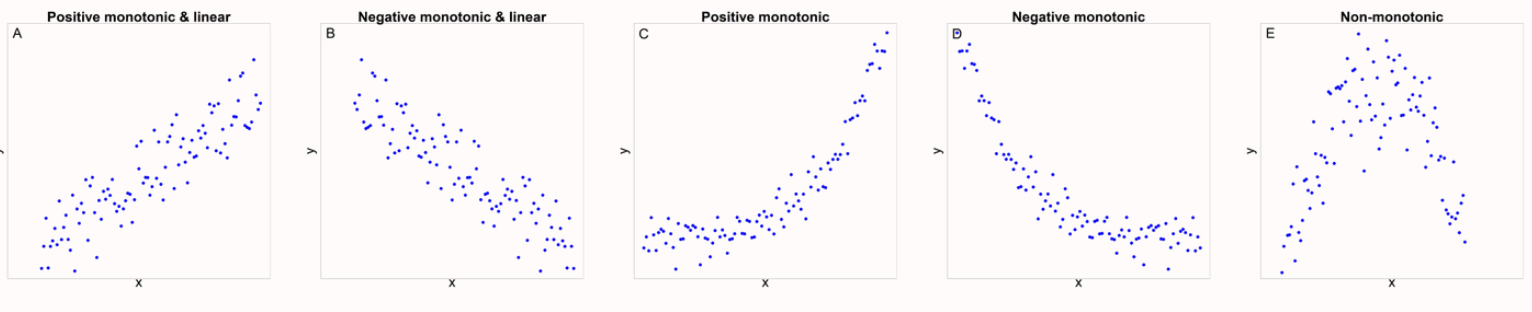
Linear와 비슷한거 아니냐고? 비슷하지만 Linear는 값이 증가/감소하는 양도 비슷하지만 monotonic은 증가량은 상관 없다. Monotonic 이 조금 더 넓은 개념이라고 생각하면 된다.

monotonic 스택, 큐, 덱

좋아 이제 Monotonic이 뭔지 알았다. 근데 스택, 큐, 덱 자료구조가 Monotonic하다는 것은 무슨 의미일까?

그것은 스택, 큐, 덱의 자료구조가 “모노톤”하다는 것을 의미한다.

즉, 자료 구조 내의 요소들이 증가 또는 감소하는 것을 유지하며 정렬되어 있다는 것이다.

모노톤 스택

스택은 LIFO(Last In First Out) 자료 구조이기에 스택의 최상위 요소를 제거하면서 단조 증가/감소 순서를 유지한다. 새로운 요소는 항상 최상위에 추가된다.

• 단조 증가 스택 (Monotone Increasing Stack): 스택에 새로운 요소를 추가할 때, 그 요소가 스택의 최상위 요소보다 작거나 같을 때까지 기존 요소들을 제거한다.

  // 자료 배열을 순회
  for (int i = 0; i < 자료.length(); i++) {
      // 스택의 최상위 요소가 현재 요소보다 크면 pop()
      while (!stack.isEmpty() && stack.peek() > 자료[i]) {
          stack.pop();
      }
      // 현재 요소를 스택에 추가
      stack.push(자료[i]);
  }

• 단조 감소 스택 (Monotone Decreasing Stack): 스택에 새로운 요소를 추가할 때, 그 요소가 스택의 최상위 요소보다 클 때까지 기존 요소들을 제거한다.

  for (int i = 0; i < 자료.length(); i++) {
      while (!stack.isEmpty() && 자료[stack.peek()] <= 자료[i]) {
          stack.pop();
      }
      stack.push(i);
  }

적합한 문제 유형:

• Nearest Greater/Smaller Element: 배열에서 각 요소에 대해 오른쪽(또는 왼쪽)에서 가장 가까운 더 큰(또는 더 작은) 요소를 찾는 문제.
• Histogram Area Calculation: 히스토그램에서 가장 큰 직사각형의 넓이를 찾는 문제.

  for (int i = 0; i < heights.length; i++) {
      while (!stack.isEmpty() && heights[stack.peek()] > heights[i]) {
          // 히스토그램의 높이와 너비를 계산하여 최대 직사각형 구하기
      }
      stack.push(i);
  }

• Stock Span Problem: 주식 가격 배열에서 각 날에 대해 이전 연속적인 날 중 주식 가격이 낮았던 날의 수를 계산하는 문제.

모노톤 큐

큐: 기본적인 큐는 FIFO(First In First Out) 자료 구조이기에 마지막 요소를 제거하면서 단조 증가 순서를 유지합니다.

• 단조 증가 큐 (Monotone Increasing Queue): 큐에 새로운 요소를 추가할 때, 그 요소가 큐의 마지막 요소보다 작거나 같을 때까지 제일 앞 요소들을 제거한다.

  // 자료 배열을 순회
  for (int i = 0; i < 자료.length(); i++) {
      // 큐의 마지막 요소가 현재 요소보다 크면 제거
      while (!queue.isEmpty() && queue.peek() > 자료[i]) {
          queue.poll();
      }
      // 현재 요소를 큐에 추가
      queue.offer(자료[i]);
  }

• 단조 감소 큐 (Monotone Decreasing Queue): 큐에 새로운 요소를 추가할 때, 그 요소가 큐의 마지막 요소보다 클 때까지 기존 요소들을 제거한다.

  for (int i = 0; i < 자료.length(); i++) {
      while (!queue.isEmpty() && 자료[queue.peekLast()] <= 자료[i]) {
          queue.pollLast();
      }
      queue.offer(i);
  }

적합한 문제 유형:

• Sliding Window Maximum/Minimum: 주어진 배열에서 크기가 k인 슬라이딩 윈도우에서 각 윈도우의 최대값 또는 최솟값을 찾는 문제.

  for (int i = 0; i < 자료.length(); i++) {
      while (!queue.isEmpty() && queue.peekLast() < 자료[i]) {
          queue.pollLast();
      }
      queue.offer(i);
      if (i >= k - 1) {
          // 슬라이딩 윈도우의 최대값을 찾기 위해 첫 번째 요소를 사용
      }
  }
  

모노톤 덱

덱은 양쪽 끝에서 삽입, 삭제가 가능한 자료구조이기에 모노톤 스택과 비슷하게 구현할수도, 모노톤 덱과 비슷하게 구현할 수도 있다.

• 단조 증가 덱 (Monotone Increasing Deque): 덱에 새로운 요소를 추가할 때, 그 요소가 덱의 마지막 요소보다 작거나 같을 때까지 기존 요소들을 제거

  // 자료 배열을 순회
  for (int i = 0; i < 자료.length(); i++) {
      // 덱의 마지막 요소가 현재 요소보다 크면 제거
      while (!deque.isEmpty() && deque.peekLast() > 자료[i]) {
          deque.pollLast();
      }
      // 현재 요소를 덱의 마지막에 추가
      deque.offerLast(자료[i]);
  }

  요소가 앞, 뒤에서 삽입/삭제가 가능하지만 해당 예시에서는 마지막 요소를 제거하고 새로운 요소를 뒤에 추가하는 방식으로 구현
  
• 단조 감소 덱 (Monotone Decreasing Deque): 덱에 새로운 요소를 추가할 때, 그 요소가 덱의 마지막 요소보다 클 때까지 기존 요소들을 제거

  for (int i = 0; i < 자료.length(); i++) {
      while (!deque.isEmpty() && 자료[deque.peekLast()] <= 자료[i]) {
          deque.pollLast();
      }
      deque.offerLast(i);
  }

적합한 문제 유형:

• 모노톤 스택에 슬라이딩 윈도우가 추가된 유형

  import java.util.Deque;
  import java.util.LinkedList;
  
  public int[] maxSlidingWindow(int[] nums, int k) {
      if (nums == null || nums.length == 0) return new int[0];
      
      int n = nums.length;
      int[] result = new int[n - k + 1];
      Deque<Integer> deque = new LinkedList<>();
      
      for (int i = 0; i < n; i++) {
          // Deque의 앞에 있는 요소가 윈도우 범위 밖에 있는 경우 제거
          if (!deque.isEmpty() && deque.peekFirst() < i - k + 1) {
              deque.pollFirst();
          }
          
          // Deque의 뒤에 있는 요소가 현재 요소보다 작으면 제거
          while (!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {
              deque.pollLast();
          }
          
          // 현재 요소의 인덱스를 Deque에 추가
          deque.offerLast(i);
          
          // 윈도우의 첫 번째 요소부터 최대값을 결과 배열에 저장
          if (i >= k - 1) {
              result[i - k + 1] = nums[deque.peekFirst()];
          }
      }
      
      return result;
  }
  

결론

모노톤 스택, 큐, 덱은 특정 조건에 맞는 알고리즘을 구현할 때 매우 유용한 자료 구조이다.

이러한 유형의 문제를 알고있고 해당 자료 구조를 사용한다면, 당황하지 않고 알고리즘을 더 쉽게 생각해낼 수 있을 것이다!