이미지 생성 모델

* 생성 모델에 대한 기초적인 내용은 여기를 참조하자.

GAN

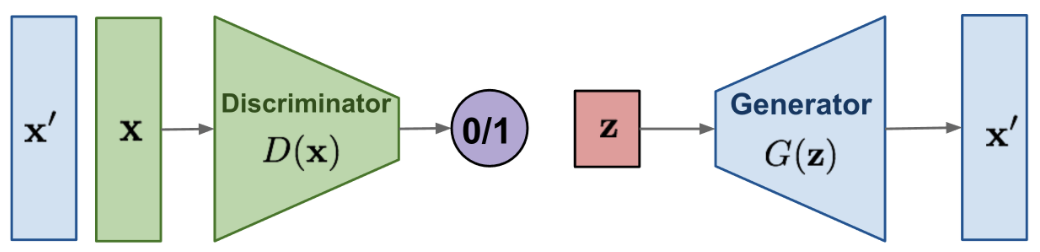
GAN(Generative Adversarial Networks)은 판별자(discriminator)와 생성자(generator)를 적대적으로 학습하는 모델 구조이다. 판별자는 입력 이미지가 생성된 이미지인지 진짜 이미지인지를 잘 판별하도록 학습하고, 생성자는 잠재 변수 z를 입력으로 받아서 학습 데이터의 분포에 가까운 이미지를 생성하도록 (즉, 진짜 이미지처럼 생성하도록) 학습한다. 다시 말하면 데이터의 생성 여부 판단 가능성을 "판별자는 maximize"하도록, "생성자는 minimize"하도록 학습하는 것이다.

cGAN

cGAN(conditional Generative Adversarial Networks)은 기존의 GAN에 조건을 주입해서 학습하는 구조이다. 주어진 조건에 따라 이미지 생성이 가능하다.

Pix2Pix

Pix2Pix는 cGAN의 일종으로 조건으로 이미지를 받는 모델이다. 학습을 위해 서로 매칭되는 paired image 쌍이 필요하며, 이미지를 조건으로 이미지를 변환한다.

CycleGAN

Pix2Pix 방식처럼 paired image를 구축하는 것은 어려운 측면이 있다. 따라서 CycleGAN에서는 unpaired image로도 학습이 가능하도록 cycle consistency loss를 제안했다.

❓ paired image와 unpaired image는 무엇이 다른가?

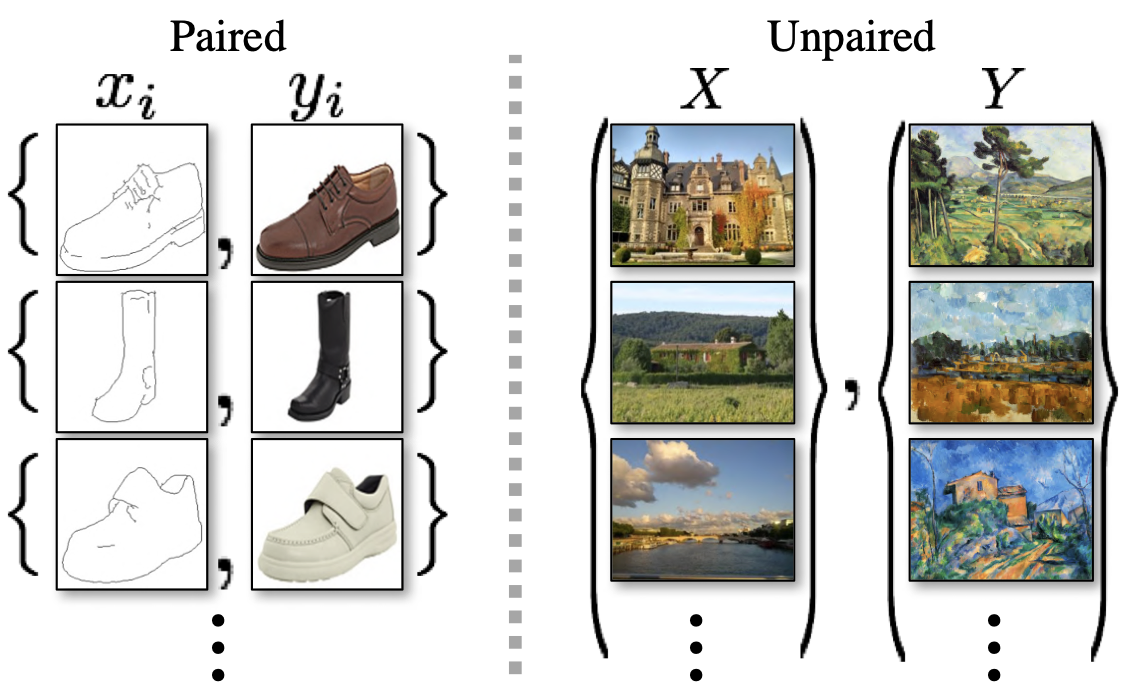
위의 이미지 예시를 보면 바로 이해가 될 것이다. Pix2Pix에서 사용하는 paired image는 변환 전후의 정확한 대응 관계가 있는 이미지 쌍이다. 구두 한 짝의 스케치 이미지 - 해당 구두 한 짝의 실제 사진 쌍, 장화 한 짝의 스케치 이미지 - 해당 장화 한 짝의 실제 사진 쌍과 같이, 1:1로 직접적으로 관련이 있다.
이에 반해 unpaired image는 한 쌍의 이미지가 1:1로 직접적으로 관련되지 않는 이미지이다. 성의 실제 사진 - 숲의 유화 이미지 쌍, 낮의 강 사진 - 밤의 저택 유화 이미지 쌍처럼 두 이미지가 직접 관련은 없다. 그러나 이는 두 이미지가 전혀 관련성이 없이 무작위로 매치되었다는 의미는 아니다. 이 이미지 쌍들은 1:1 직접 매칭이 없을 뿐 "실제 사진"과 "유화 이미지"라는 도메인의 분포 차이를 학습시키려는 쌍이다.

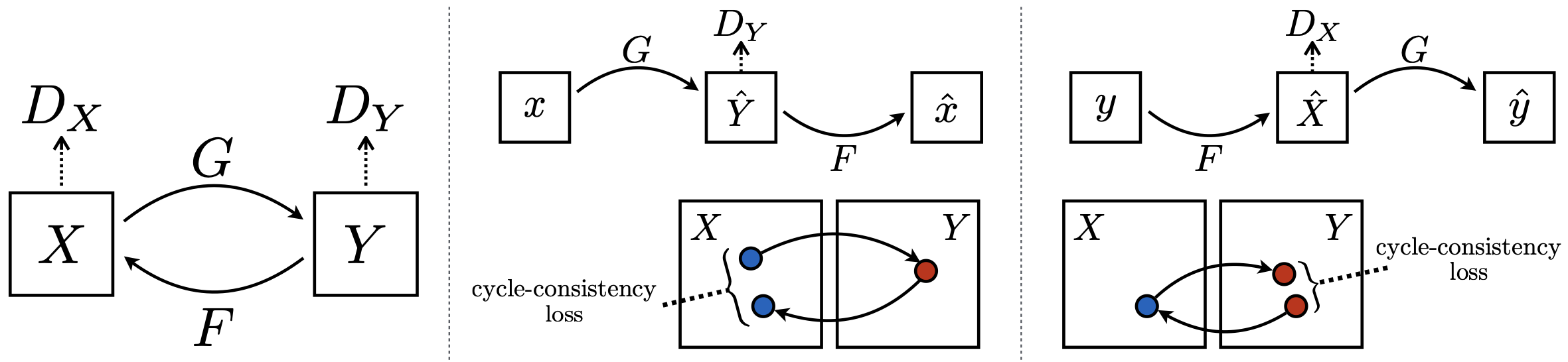
다시 본론으로 돌아와서, cycle consistency loss란, 직접적으로 1:1 매칭이 되지 않는 unpaired image에 대해 이미지 생성을 잘 학습시키기 위한 손실 함수이다. 기본적인 아이디어는 도메인 X에서 도메인 Y로 변환한 후, 이를 다시 도메인 X로 복구했을 때 (X → Y → X) 원본 이미지와 최대한 비슷하게 만들어야 한다는 것이다. 반대로, 도메인 Y에서 도메인 X로 변환한 후, 이를 다시 도메인 Y로 복구했을 때 (Y → X → Y)에도 마찬가지로 원본 이미지와 최대한 비슷하게 만들어야 한다. 이러한 과정을 거치면, 변환의 신뢰성과 일관성을 보장할 수 있을 것이라는 아이디어이다.
이 때 X에서 Y로 변환하는 생성자를 G라고 하고, Y에서 X로 변환하는 생성자를 F라고 하자. 그리고 도메인 X에서 진짜 이미지인지 생성된 이미지인지 판별하는 판별자를 $D_X$, 도메인 Y에서 생성된 이미지인지 생성된 이미지인지 판별하는 판별자를 $D_Y$라고 하자. 학습을 위한 목적 함수($L(G, F, D_X, D_Y)$)는 $L_{GAN}$과 $L_{cyc}$로 구성된다. $L_{GAN}$은 GAN 학습을 위한 adversarial training loss이고, $L_{cyc}$은 cycle consistency loss로, 생성한 이미지를 다시 원본 이미지로 생성했을 때 consistency를 유지하기 위한 손실 함수이다. 이 목적 함수를 이용하면 unpaired image 쌍을 이용할 때에도 학습을 잘 시킬 수 있게 된다.

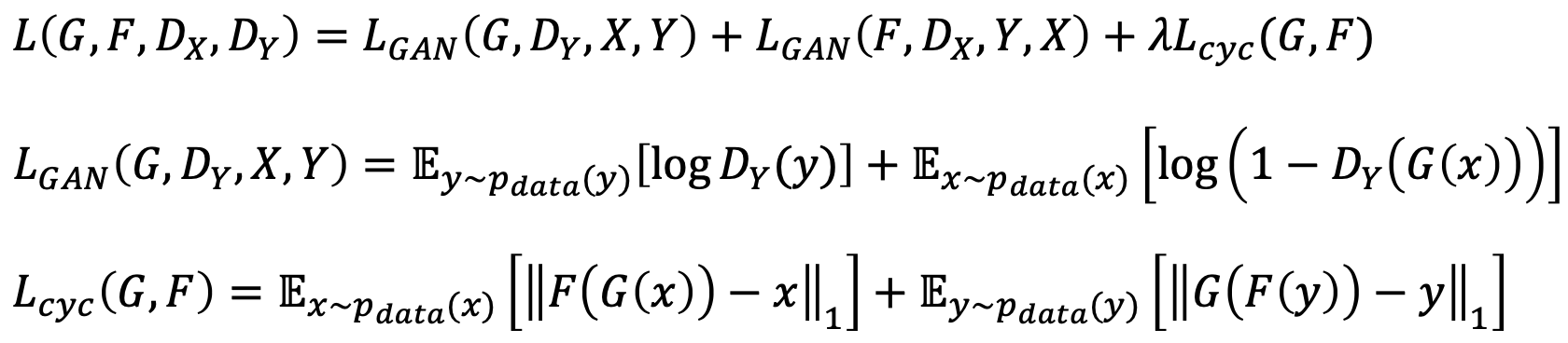
StarGAN

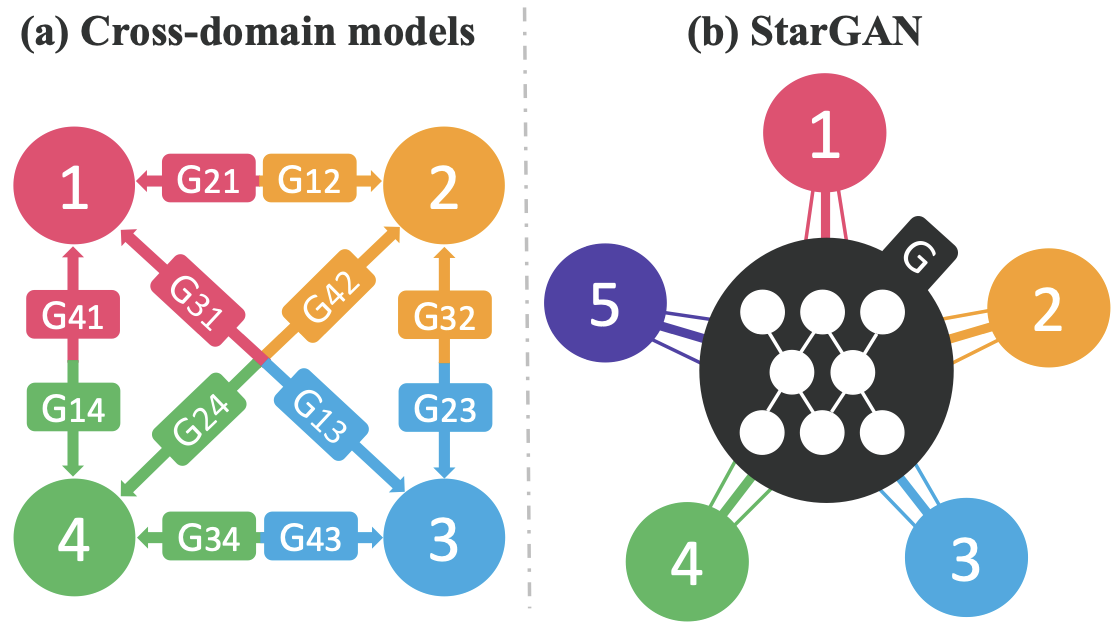
사용자의 수요에 따라, 이미지 생성 모델은 다양한 도메인을 다뤄야 할 것이다. 그러나 도메인 별로 생성 모델을 만드는 것은 어려운 일이다. 이에 단일 생성 모델만으로 여러 도메인을 반영할 수 있는 구조를 제안한 것이 StarGAN이다.

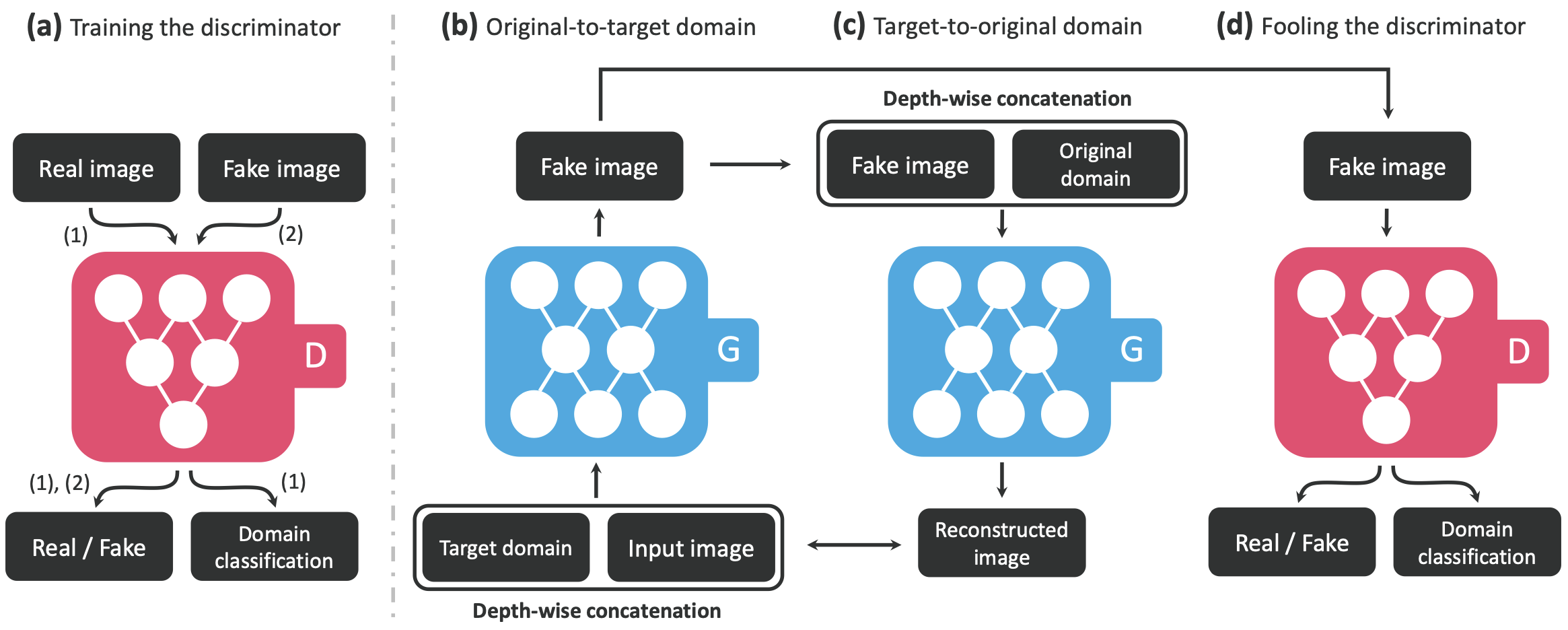
StarGAN에서는 하나의 생성 모델로 여러 도메인을 반영하도록 목적 함수에 adversarial training loss, classification loss, cycle consistency loss를 사용한다.

우선 판별자의 목적 함수 $L_D$는 아래와 같이 나타난다.

$L_D = -L_{GAN} + \lambda_{cls} L_{cls}^r$

$where$ $L_{GAN}$ = adversarial training loss
    $\lambda_{cls}$ = $L_{cls}$ (classification loss; 도메인을 분류하기 위한 loss) 의 중요도를 조정하는 가중치. 생성된 이미지가 목표 속성을 만족하도록 학습시킬 때 사용되는 term
    $L_{cls}^r$ = real image의 classification loss. real image의 속성(label)을 정확히 예측하기 위한 손실 함수

생성자의 목적 함수 $L_G$는 아래와 같이 나타난다. (중복되는 term 설명은 $L_D$에서 참고)

$L_G = L_{GAN} + \lambda_{cls} L_{cls}^f + \lambda_{rec} L_{rec}$

$where$ $L_{cls}^f$ = fake image의 classification loss. fake image가 올바른 속성(label)을 가지도록 학습하는 손실 함수
    $\lambda_{rec}$ = reconstruction loss의 가중치. 이미지가 원래 속성으로 복원될 수 있도록 학습하는 가중치
    $L_{rec}$ = cycle consistency loss

각 term이 구체적으로 어떻게 계산되는지는 논문을 참고하자. 아무튼 StarGAN에서는 이렇게 설계된 목적 함수 덕분에 하나의 생성 모델로 다양한 도메인의 이미지를 생성할 수 있게 되었다.

ProgressiveGAN

고해상도 이미지 생성 모델을 학습하기 위해서는 많은 비용이 발생한다. 따라서 적은 비용으로도 빠른 수렴이 가능하도록 저해상도 이미지 생성 구조부터 단계적으로 증강하는 모델 구조를 제안한 것이 ProgressiveGAN이다. 이미지 해상도를 키우는 과정에서 작은 해상도의 이미지와 큰 해상도의 이미지 결과를 weighted sum으로 계산하여 사용했다.

StyleGAN

StyleGAN은 ProgressiveGAN에서 이미지의 style을 조작할 수 있도록 한 것이다. style이란 이미지의 특징을 제어하는 정보로, 색상, 톤, 대비, 텍스쳐, 패턴, 디테일 같은 것을 말한다.

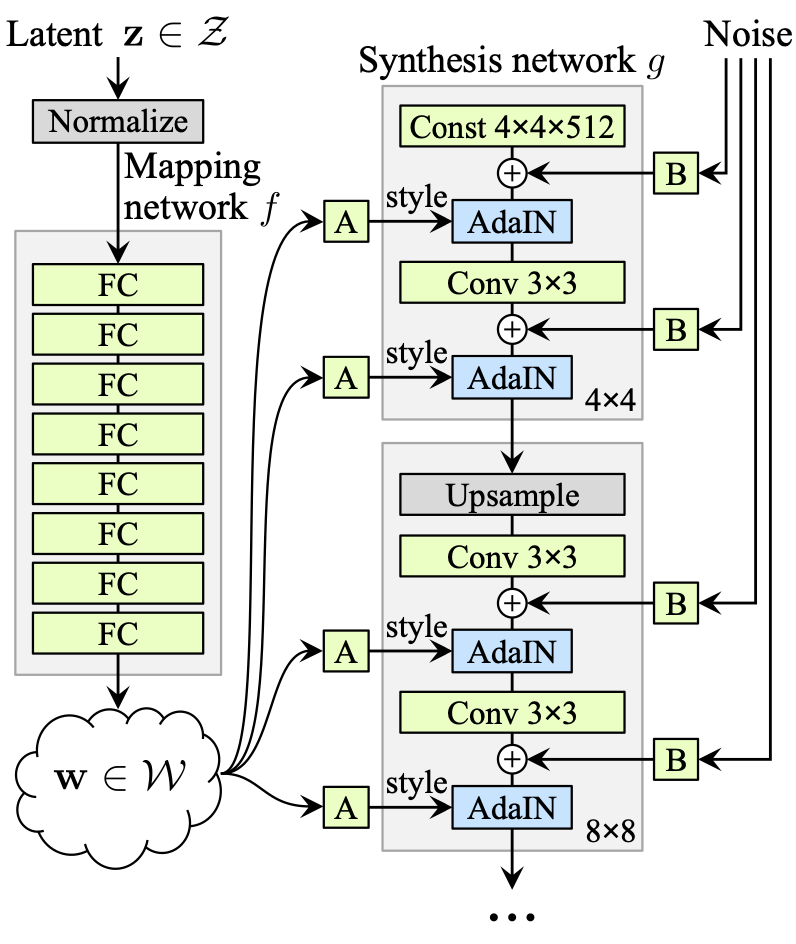
생성되는 이미지에 style을 주입하기 위해서, 기본적인 랜덤 노이즈 벡터 z가 비선형 변환을 통해 새로운 latent space W로 매핑된다. 이 때 매핑 함수 f는 데이터의 분포에 맞춰 얽힘이 풀리도록 구성한다. 이를 통해 W는 스타일 정보를 담게 된다. W에 affine transform을 적용하여 스타일 정보 $\gamma$, $\beta$를 계산하고, AdaIN을 통해 이미지 생성 네트워크의 각 레벨에 주입된다.

$AdaIN(x, \gamma, \beta) = \gamma(\frac{x-\mu(x)}{\sigma(x)}) +\beta$

AdaIN은 스타일 정보를 통해 각 레벨의 feature map의 평균값과 표준편차를 조정하여, 이미지의 스타일을 제어한다. 저해상도 레벨에서는 global style (색상, 대조 등), 고해상도 레벨에서는 local style (텍스처, 디테일 등)를 조절한다.

AutoEncoder

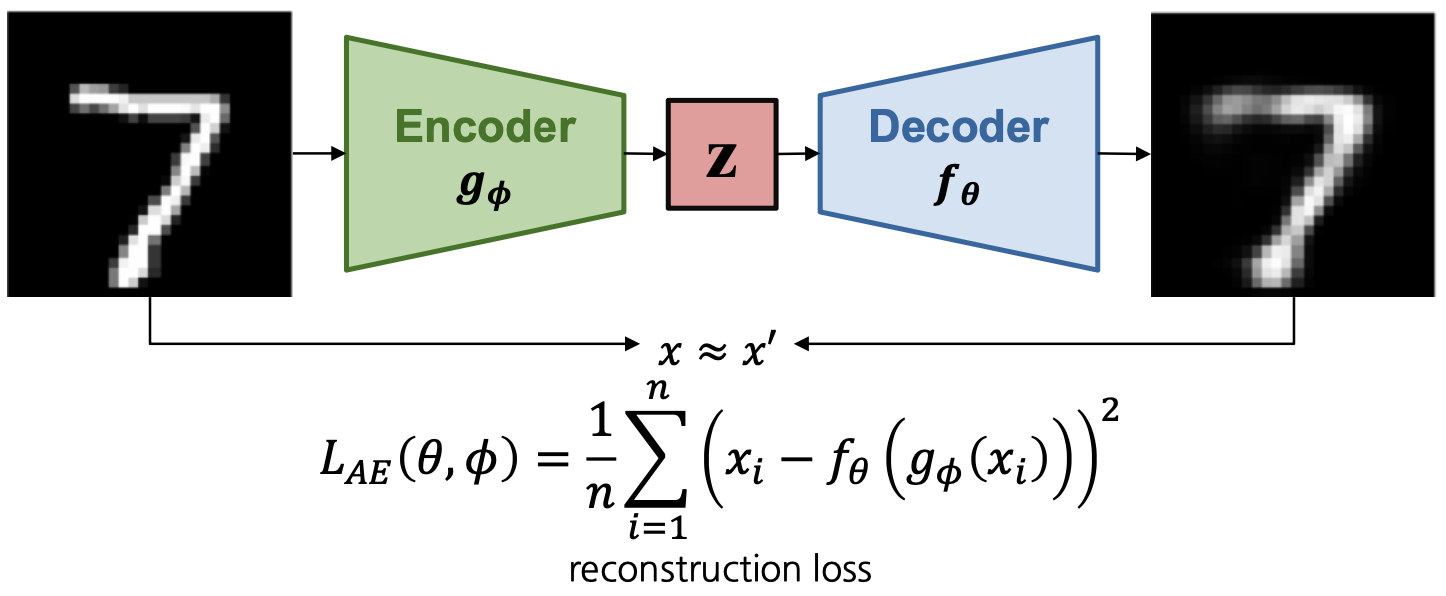
Autoencoder는 Encoder $g_{\phi}$ 와 Decoder $f_{\theta}$로 구성되어 입력 이미지를 다시 복원하도록 학습하는 모델 구조이다. Encoder는 입력 이미지를 저차원 latent space로 매핑하여 잠재 변수 z로 변환하고, Decoder는 잠재 변수를 입력으로 사용하여 원본 이미지를 복원한다.

목적 함수는 reconstruction loss인데, 일반적으로 Mean Squared Error 혹은 Mean Absolute Error를 활용한다.

Variational AutoEncoder

Variational AutoEncoder (VAE) 는 AutoEncoder과 동일하게 encoder와 decoder로 구성되어 있지만 latent space의 분포를 가정하여 학습하는 모델이다.
목적 함수는 reconstruction loss 뿐만 아니라 사전에 정의한 latent space의 분포를 학습에 반영하기 위해 KL divergence를 함께 정의한다. VAE는 생성할 이미지의 분포를 latent space로부터 학습하므로, latent space의 분포가 생성 이미지의 분포와 같도록 학습할 것이다. 이 때의 척도로 KL divergence가 사용된다.

VQ-VAE

VQ-VAE (Vector Quantized-Varitaional AutoEncoder) 는 이름에서도 나타나듯이 vector quantization (벡터 양자화) 과정을 통해 연속적인 latent space 대신 고정된 크기의 codebook에서 이산적인 벡터를 선택하여 데이터를 표현한다.

Encoder에서 입력 데이터 $x$를 압축하여 latent vector $z(x)$로 변환한다. 이 때 latent vector $z(x)$는 연속적인 공간에 존재한다. 이후 vector quantization 과정을 통해 latent vector $z(x)$를 미리 정의된 codebook (벡터 집합) 내의 가장 가까운 이산 벡터로 매핑한다. Decoder에서는 양자화된 벡터 $z_q(x)$를 사용하여 원래 데이터로 복원한다.

VQ-VAE의 손실 함수는 reconstruction loss, commit loss, codebook update loss로 구성된다.

$L = L_{rec} + L_{commit} + L_{codebook}$

$where$ $L_{rec}$ = 입력 데이터와 복원된 데이터 간의 차이 측정,
        $L_{commit}$ = encoder의 출력 $z(x)$가 코드북 벡터 $z_q(x)$에 가까워지도록 유도하는 term. encoder가 코드북의 벡터를 잘 활용하도록 한다.
        $L_{codebook}$ = 코드북 벡터 $z_q(x)$가 encoder의 출력 $z(x)$에 가까워지도록 유도하는 term. 코드북이 데이터 분포를 더 잘 표현하게 만든다. stop gradient (역전파 차단) 항이 있어서 $z_q(x)$만 업데이트 되고 encoder는 업데이트 되지 않도록 한다.

자세한 계산식은 논문을 참고하도록 하자. VQ-VAE는 벡터 양자화 과정을 도입함으로써 고품질 데이터 생성과 명확한 데이터 표현을 제공하며, 이미지, 음성, 텍스트 생성 등 다양한 분야에 응용된다. 우리가 잘 아는 DALL·E도 VQ-VAE를 활용한 것이라고 한다!

Diffusion Model

DDPM

DDPM(Denoising Diffusion Probabilistic Models)은 입력 이미지를 forward process를 통해 잠재 공간으로 변환하고 reverse process로 복원하여 이미지를 생성하는 모델이다. forward proces에서는 점진적으로 Gaussian noise를 추가하여 잠재 공간으로 매핑하고, reverse process에서는 forward process에서 추가된 노이즈를 추정하여 제거한다.

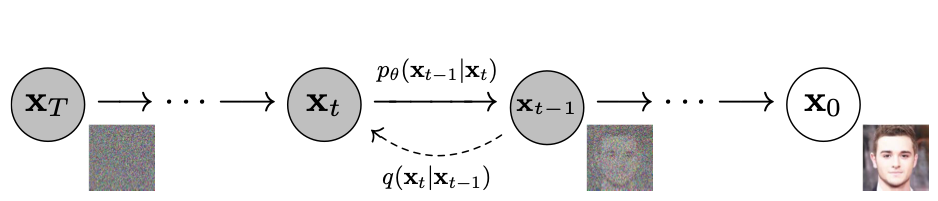
DDIM

DDPM은 노이즈를 추가하고 제거하는 과정에서 거치는 step이 많아서 이미지 생성을 위해 시간이 많이 소요된다. DDIM (Denoising Diffusion Implicit Models) 는 이러한 한계를 보완하기 위해서 noise 추정 방식을 변화시킨 모델이다. DDPM이 직전 데이터를 기반으로 특정 분포 (Gaussian)에서 노이즈를 랜덤 샘플링하는 방식이었다면 (stochastic sampling process), DDIM은 몇 단계 이전의 데이터도 함께 고려하여 고정된 규칙에 따라 노이즈를 제거(deterministic sampling process, non-Markovian diffusion process)한다. 따라서 더 적은 단계로도 고품질의 샘플링이 가능해진다.

Classifier Guidance

Classifier Guidance (CFG) 는 노이즈를 제거한 이미지가 특정 클래스에 속할 확률이 높아지도록 노이즈를 샘플링하여 제거하는 이미지 생성 모델이다. (→ score-based conditioning trick) 그러나 기존의 diffusion pipeline에 classifier가 추가되어 복잡해졌고, 모든 step에 대해 clssifier가 필요하다는 단점이 있다.
이를 보완하기 위해 Classifier-free Guidance에서는 Classifier Guidance의 식을 conditional socre, unconditional score로 분해하여 재정의하였다. 그래서 noise level마다 classifier를 학습할 필요 없이 class에 대한 guidance를 가중치로 조정할 수 있게 되었다.

Latent Diffusion Model

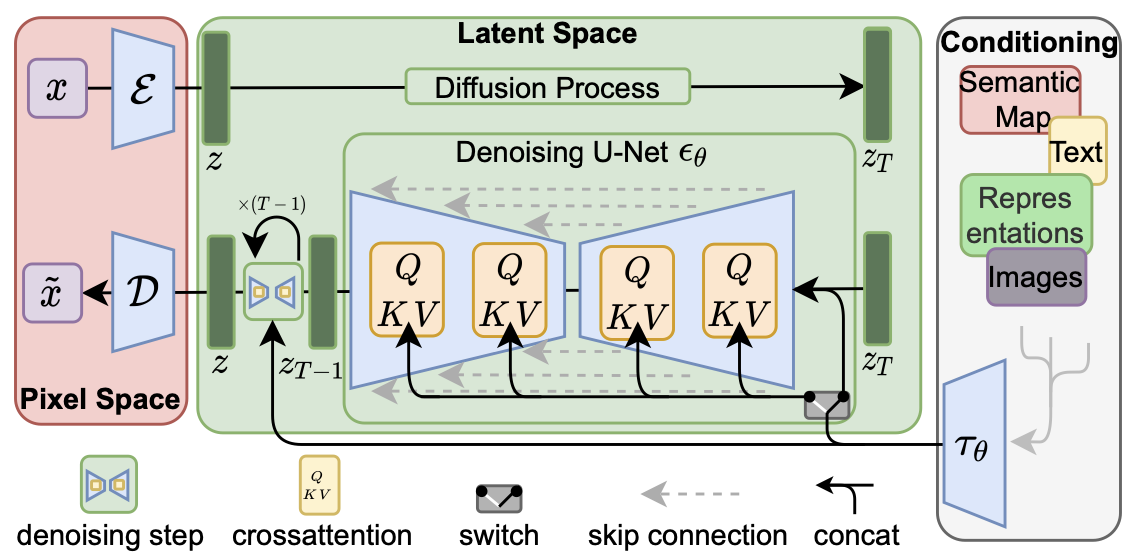
Latent Diffuision Model (LDM) 은 latent space에서 diffusion 과정을 수행하여 고해상도 이미지를 효율적으로 생성하는 모델이다. 기존의 diffusion model는 pixel space에서 노이즈를 더하고 제거했지만, LDM은 latent space에서 노이즈를 처리하여 계산 효율성을 향상시켰다.
encoder를 통해 입력 이미지가 latent space로 입력되고, latent space에서 diffusion 모델을 적용해 노이즈를 더하고 제거해서 생성된 이미지를 decoder에서 원본 이미지 공간으로 복원한다. 이 때 cross attention을 통해 latent space에 condition embedding을 반영할 수 있다. 이는 입력한 조건에 부합한 이미지가 생성되도록 조정한다.

Stable Diffusion

stable diffusion은 LDM을 기반으로 설계된, text-to-image 생성에 특화된 모델이다. text prompt를 기반으로 고품질 이미지를 생성한다. 전반적인 architecture는 LDM을 기반으로 했기 때문에 LDM과 거의 유사하다.

Stable Diffusion의 구조

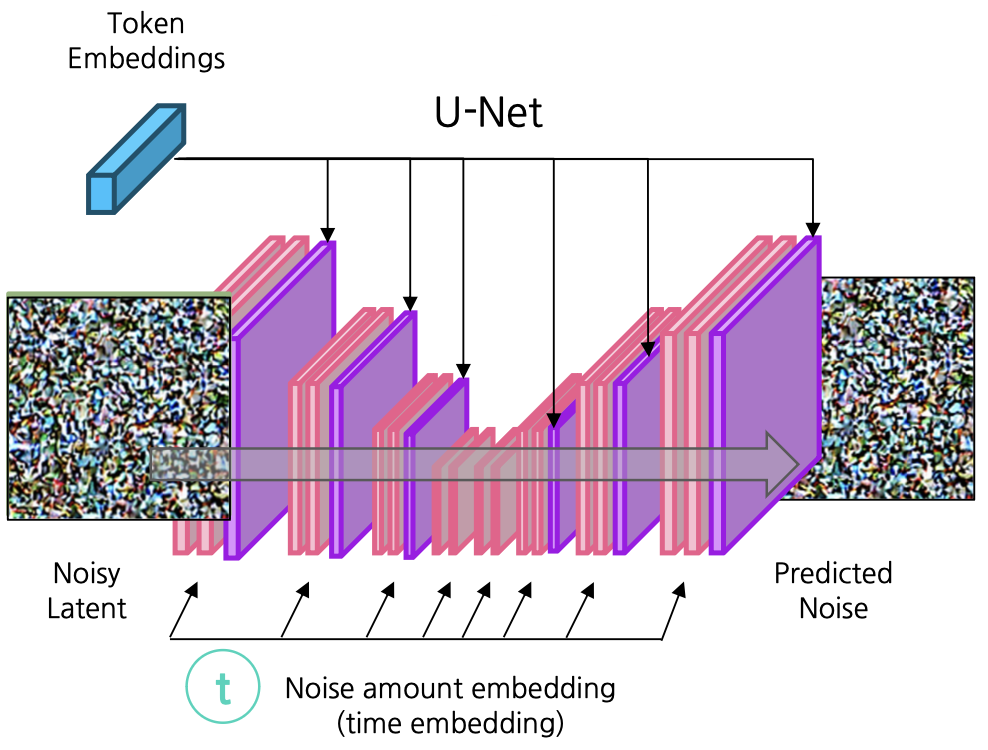
여기서는 latent space를 image information creator라고 하겠다. image information creator를 살펴보면, U-Net 구조가 noise의 prediction을 담당한다. 먼저, input latent와 noise를 주입할 정도를 input으로 받아서 noise scheduler를 거쳐 해당하는 noise를 입힌 noisy latent를 생성한다.
그러면 noisy latent와 time embedding을 input으로 받고, text encoder의 결과물인 token embedding과 cross attention을 이용해 (key, value : token embedding, query : noisy latent) 결합한다. 이 정보들을 이용해 가해진 noise를 예측한다.
conditioning에서는 text input을 CLIP text encoder를 이용해 embedding으로 바꾸고, latent space에서 noisy latent와 결합할 수 있도록 한다.

Stable Diffusion의 학습

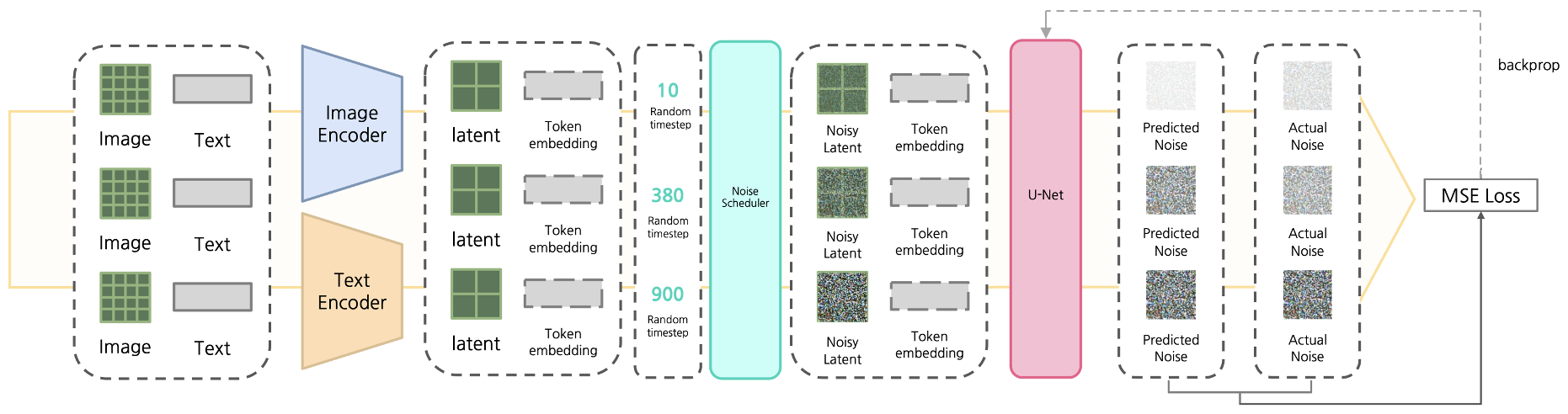
stable diffusion을 학습시킬 때에는 먼저 input data (이미지, 텍스트)를 각각의 encoder를 통해 latent로 변환한다. 그 후 image latent를 random한 timestep만큼 noise scheduler를 이용해 noise를 가한다. noisy latent와 token embedding, time step을 U-Net에 입력하면 U-Net은 가해진 noise를 예측한다. 예측한 noise와 실제 noise를 비교하여 그 차이를 MSE loss로 계산하여 이 loss가 작아지도록 학습시킨다.

Stable Diffusion의 inference

1. text-to-image task
   stable diffusion이 텍스트를 입력받아 이미지를 생성할 때에는 가장 먼저 Gaussian noise 상태에서 시작한다. input text의 token embedding을 입력받아서 학습된 U-Net을 통해 noise를 예측한다. 이렇게 예측된 noise를 제거하는 과정을 반복하고 최종 latent를 decoder를 통해 이미지로 변환하여 생성된 이미지를 반환한다.

2. inpainting task
   inpainting 작업의 경우 input 이미지에서 변환된 latent에 noise를 가한 noisy latent에서 시작한다. 이 때 input 이미지의 영향을 크게 하고 싶다면 time step을 작게 하여 noise를 적게 더하고, input 이미지의 영향을 줄이고 싶다면 time step을 크게 하여 noise를 많이 더한다. 이후는 text-to-image와 동일하게 noise를 예측해서 제거해나가는 과정을 통해 이미지를 생성한다.

Stable Diffusion 2

• Stable diffusion 2는 기존 Stable diffusion보다 생성 이미지 해상도가 높아졌고 (512 $\times$ 512 → 768 $\times$ 768) text encoder를 CLIP에서 OpenCLIP으로 업데이트 하였다.
• Stable diffusion 2.0-v는 기존의 noise prediction이 아닌 v-prediction (v: velocity = 노이즈와 원본 데이터 사이의 혼합 정도)를 이용해 학습한 버전이다.
• super-resolution upscaler diffusion model을 덧붙여서 2048 $\times$ 2048 혹은 그 이상의 고해상도 이미지를 생성할 수 있게 되었다.
• depth guided image generation으로 text와 depth의 정보를 동시에 담은 이미지를 생성할 수 있게 되었다.

Stable Diffusion XL

• 보다 현실적인 이미지 생성
• 2 stage model (base + refiner)
• text encoder 2개
• 정방형에서 벗어나 다양한 비율의 이미지 생성 가능
• SDXL Turbo : Adversarial Diffusion Distillation 방법론을 적용하여 추론 속도를 향상시킨 모델 (one-step generation)

이미지 생성 모델의 평가

Inception Score

Inception score는 생성된 이미지의 fidelty(질)와 diversity를 측정하는 지표이다. fidelty는 생성된 이미지가 특정 class를 명확히 표현하는지를 평가하는데, 생성된 이미지가 명확한 class를 같는다면 해당 이미지의 likelihood 분포는 특정 class에 치우친 분포로 나타날 것이다. diversity는 다양한 class가 생성되고 있는지를 평가하는데, 생성된 이미지들이 다양한 class를 가진다면 이미지에 대한 likelihood 분포의 합 (marginal distribution)은 균일한 분포로 나타날 것이다.
따라서 두 분포의 KL divergence 값을 구하면 inception score를 계산할 수 있는데, inception score 값이 클수록 두 분포가 다르다는 것을 의미하므로 이미지가 잘 생성되는 것으로 평가할 수 있다.

FID Score

FID (Frechet Inception Distance) score는 Inception Network라고 하는 pre-trained image classification model을 이용해 추출한 벡터 간의 Frechet distance를 계산하는 점수이다. Inception Network를 이용해 구한 실제 이미지의 embedding과 생성 이미지의 embedding 간의 Frechet distance를 이용해 FID score를 계산한다. FID score 수치가 작을수록 이미지가 잘 생성된 것이다.

CLIP Score

이미지와 캡션 사이의 상관 관계를 평가하는 지표이다. 캡션으로부터 CLIP을 이용해 생성된 embedding과 이미지로부터 CLIP을 이용해 생성된 embedding 간의 유사도 (cosine similarity)를 계산하여 평가한다. CLIP score 수치가 클수록 이미지가 잘 생성된 것이다.

References

https://lilianweng.github.io/posts/2021-07-11-diffusion-models/
https://arxiv.org/abs/1703.10593
https://arxiv.org/abs/1711.09020
https://arxiv.org/abs/1812.04948
https://stanford.edu/~jlmcc/papers/PDP/Volume%201/Chap8_PDP86.pdf
https://arxiv.org/abs/2006.11239
https://arxiv.org/abs/2011.13456
https://arxiv.org/abs/2112.10752