Mathematical Correctness of Bubble Sort : 버블 정렬은 수학적으로 왜 성립하는가?

Series : CS + Math

CS + Math 시리즈의 첫 글이다. 사실 CS를 공부하면 공부할수록 CS 속에서 수학이 차지하는 부분이 크다는 것을 느낄 수 밖에 없다. 그래서 CS를 공부하면서 떠올랐던 수학적 Idea들, 아니면 수학을 공부하면서 찾았던 CS와의 연관성들을 한 번 정리해보고 싶어서 이 시리즈를 시작하게 되었다.

Sorting == Permutation

What is Sorting Problem?

많은 사람들에게 프로그래밍을 공부하면서 가장 처음 접한 실질적 문제 상황이나 알고리즘이 무엇이냐고 물어볼 때, 대부분은 정렬(Sorting) 문제를 말할 것이다.

우리는 흔히 Sorting Problem, 혹은 Sorting Algorithm을 다음과 같이 정의할 것이다.

Sorting Algorithm
해당 Input이 주어졌을 때, 해당 Output을 만들어내는 알고리즘
Input : 임의의 sequence $S=<a_1, a_2, ..., a_n>$
Output : $S$의 원소들로 구성된 또 다른 sequence $S'=<a_1', a_2',..., a_n'>$
(이때, $a_1', ... , a_n'$은 정해진 규칙이나 순서 에 의해 오름차순 (혹은 내림차순)으로 배열되어 있다. 대부분의 경우, $S$의 원소들이 정수이며 $a_1', ... , a_n'$은 $a_1' \le ... \le a_n'$, non-decreasing order로 배열되어 있다.)

What is Permutation?

그렇다면 이 문단의 제목에 나와 있는 "Permutation"은 무엇을 말하는걸까?
대부분의 사람들이 확통에서 배우는 이 순열을 떠올릴 것이다.

$_{n}\mathrm{P}_{k} = \frac{n!}{(n-k)!}$

하지만 이 포스트에서 이야기하고자하는 permutation은 약간 다르다.
(사실 군론에서의 permutation과 조합론에서의 permutation의 차이지 개념은 거기서 거기다)

한국말로는 보통 치환이라고 부르는 permutation은 다음과 같이 정의한다.

치환 (permutation)
공집합이 아닌 집합 $X$에서 자기 자신 $X$로의 일대일 대응, 혹은 전단사 함수 $\sigma : X \rightarrow X$를 $X$ 위의 치환, 혹은 순열이라고 한다.
$X = \{x_1, x_2, ..., x_n\}$일 때, $\sigma = \begin{pmatrix} ... & x_k & ... \\ ... & \sigma(x_k) & ...\\ \end{pmatrix}$와 같이 나타낸다.

즉, 쉽게 말하면 어떤 집합에 대한 원소의 재배열이다.
예를 들어서 $\{1,2,3\}$이라는 집합이 있다고 하면 가능한 치환은 총 6개일 것이다.
($\{1,2,3\}, \{1,3,2\}, \{2,1,3\}, \{2,3,1\}, \{3,1,2\}, \{3,2,1\}$)

정의 자체가 전단사 함수이기 때문에 $X$의 크기가 $n$이라고 한다면 가능한 치환의 개수는 총 $n!$개라는 것은 쉽게 유추해볼 수 있는 사실일 것이다.

Redefinition : Sorting

그런데 치환의 정의가 원소의 재배열이라고 한다면, 결국 이건 sorting 문제와 매우 유사하다는 것을 쉽게 알 수 있을 것이다.

그렇다면, 우리는 대부분의 일반적인 경우에서 Sorting Algorithm을 다음과 같이 재정의할 수 있을 것이다.

Sorting Algorithm
임의의 정수들의 집합 $S=<a_1, a_2, ..., a_n>$에 대하여, 다음을 만족하는 $S$ 위의 치환(permutation) $\sigma : S \rightarrow S$, 혹은 이를 찾는 과정을 말한다.

$\sigma = \begin{pmatrix} ... & a_k & ... \\ ... & \sigma(a_k) & ...\\ \end{pmatrix}$일 때, $\sigma(a_1) \le ... \le \sigma(a_n)$.

Properties of Permutation

이렇게 Sorting Problem을 치환을 이용해 재정의해봤으니, 치환에 대해 조금 더 자세히 알아보자.

Orbit, Cycle and Transposition

다음과 같은 Permutation 하나를 생각해보자.

$X = \{1, 2, 3, 4, 5, 6, 7, 8\}$에 대해서,
$\sigma = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 3 & 8 & 6 & 7 & 4 & 1 & 5 & 2 \\ \end{pmatrix}$

1부터 8까지의 각 숫자들이 어떤 숫자로 치환되는지를 그림으로 표현해보면 다음과 같이 3개의 사이클이 생기는 걸 볼 수 있다.

이렇게 치환 내에 생기는 사이클들을 표현하기 위해서, 궤도(orbit) 라는 개념이 정의된다.

궤도 (orbit)
집합 $X$ 위의 치환 $\sigma$와 $x \in X$에 대하여, $\sigma^n(x) = (\sigma \circ \sigma \circ ... \circ \sigma)(x)$이라고 할 때, 중복집합이 아닌 $X$의 부분집합

$orb_\sigma(x) = \{s\ | \ s=\sigma^k(x) (k = 0, 1, 2, ...)\}$

를 $x$를 포함하는 궤도라고 한다.

위의 예시로 쉽게 보자면, 1에 대해서 생각해 봤을 때
$\sigma(1) = 3, \sigma(\sigma(1)) = 6, \sigma(\sigma(\sigma(1))) = 1$ 이기 때문에

$orb_\sigma(1) = \{1, 3, 6\}$로 볼 수 있는 것이고,
또한 $orb_\sigma(1) = orb_\sigma(3) = orb_\sigma(6)$일 것도 쉽게 유추할 수 있다.

이렇게 임의의 치환에서 우리는 여러 개의 궤도가 존재한다는 것을 볼 수 있는데, 그렇다면 치환 전체가 cycle인 치환도 존재할 수 있을 것이다.

예를 들어,
$X = \{1, 2, 3, 4\}$에 대해서,

$\sigma = \begin{pmatrix} 1 & 2 & 3 & 4 \\ 3 & 2 & 1 & 4\\ \end{pmatrix}$ 와 같은 치환이 있다면, 이 치환은 2와 4는 고정된 상태로
$orb_\sigma(1) = \{1, 3\} = orb_\sigma(3)$를 이루고 있기 때문에 치환 자체가 하나의 사이클인 형태로 볼 수 있다.

이러한 특수한 permutation들을 우리는 cycle이라고 부른다.

순환치환 (cycle)
어떤 치환 $\sigma$가 원소를 2개 이상 포함한 궤도 $orb_\sigma$를 단 하나만 가지고 있을 때, $\sigma$를 순환치환이라고 한다.
만약, 순환치환 $\sigma$에서 $i_1 \rightarrow i_2 \rightarrow ... \rightarrow i_r \rightarrow i_1$와 같이 순환적 변환이 형성된다면, 해당 순환치환은 간단하게 $(i_1\ i_2 \ ... \ i_r)$로 나타낸다.

그렇다면 여기서 우리가 직관적으로 알아낼 수 있는 치환의 특징이 있는데, 바로 모든 치환은 여러 개의 순환치환들로 구성되어 있다는 것이다.

이게 무슨 말이냐 하면, 아까 우리가 위에서 본 이 치환

$X = \{1, 2, 3, 4, 5, 6, 7, 8\}$에 대해서,
$\sigma = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 3 & 8 & 6 & 7 & 4 & 1 & 5 & 2 \\ \end{pmatrix}$

에서 원소가 2개 이상인 orbit은 총 3개가 있었다 : $\{1, 3, 6\}, \{2, 8\}, \{4, 7, 5\}$.

만약 우리가 이 각각의 orbit을 새로운 치환 $\sigma_1, \sigma_2, \sigma_3$라고 생각한다면?
($\sigma_1 = \begin{pmatrix} 1 & 3 & 6 \\ 3 & 6 & 1\\ \end{pmatrix} = (1 \ 3 \ 6)$과 같은 방식으로)

$\sigma$는 사실 $\sigma_1, \sigma_2, \sigma_3$의 결합으로 표현 가능한 것이다!

이 중요한 성질을 정리해두고 다음 개념으로 넘어가보자.

Properties of Permutation (1)
임의의 permutation은 distinct한 cycle들의 결합 으로 표시가 가능하다.

이제 이 소문단의 제목에서 우리가 모르는 용어는 transposition 한 가지인데, transposition의 정의는 다음과 같다.

호환 (transposition)
순환치환들 중 항이 2개인 2항 순환치환(cycle) $(i \ j)$ 를 호환이라고 한다.

그냥 i -> j / j -> i 인 크기 2짜리 cycle이다.
이제 이 transposition을 이용한 매우 중요한 성질이 나온다.

Properties of Permutation (2)
임의의 순환치환 $\sigma = (a_1 \ a_2 \ ... \ a_n)$에 대하여,
$\sigma = (a_1 \ a_n) \ ... \ (a_1 \ a_3) (a_1 \ a_2)$ 가 성립한다.

즉, 임의의 모든 cycle은 transposition의 결합 으로 표현이 가능하다.

간단하게 이 성질이 왜 성립하는지를 생각해 보자.

만약에 크기 3짜리 cycle $(a_1 \ a_2 \ a_3)$로 생각을 해 본다면,

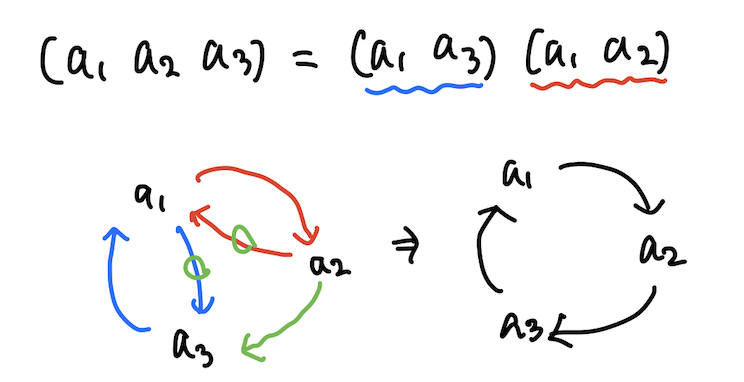
이렇게 두 개의 transposition의 결합을 통해 크기 3짜리 cycle을 만들어 낼 수 있다는 사실을 알 수 있고, 이를 귀납적으로 확장시킨다면 임의의 크기 n짜리 cycle에 대해 항상 성립하게 할 수 있다는 사실을 알 수 있다.

Properties of Permutation : Decomposition with Transposition

위에서 우리는 permutation에 대한 용어를 정리하면서, 두 가지 성질을 함께 정리해보았다.

Properties of Permutation (1)
임의의 permutation은 distinct한 cycle들의 결합 으로 표시가 가능하다.

Properties of Permutation (2)
임의의 모든 cycle은 transposition의 결합 으로 표현이 가능하다.

이 두 가지 성질을 보니, 이 두 가지 성질을 결국엔 합칠 수 있을 것이다!
이렇게 해서, 우리는 치환의 세 번째 성질이 다음과 같음을 알 수 있다.

Properties of Permutation (3)
적어도 2개 이상의 원소를 갖는 유한집합의 모든 permutation은 transposition의 결합으로 표현이 가능 하다.

즉, 모든 치환은 크기 2짜리 cycle의 결합으로 전부 바꿔버릴 수 있다는 것이다.
이 성질이 결국 이 포스트에서 이야기하고자 하는 핵심이라고 보면 된다.

Correctness of Bubble Sort

어떤 알고리즘이 모든 Input에 대해서 알맞은 Output을 내어놓을 수 있다는 것은 매우매우매우 중요할 것이다. 즉, 어떤 알고리즘이든 그 correctness를 증명할 수 있어야 한다는 것이 매우 중요하다.

그렇다면 Bubble Sort는 어떨까 ?

What is Bubble Sort?

많은 사람들이 sorting 알고리즘을 접할 때 가장 처음 접할 만한 간단한 알고리즘이라고 볼 수 있는 sorting 중 하나가 이 Bubble Sort라고 할 수 있겠다.

슈도코드를 간단히 보고 넘어가자면,

(출처 : https://www.baeldung.com/cs/bubble-sort-time-complexity)

배열 내에 있는 모든 원소쌍들에 대해서 만약 왼쪽 원소가 오른쪽 원소보다 크다면, 두 개를 swap해버리는 방식이다. 큰 원소들이 계속해서 오른쪽으로 움직이는 방식이 마치 거품과 같다하여 Bubble이라는 이름이 붙은 것으로 알고 있다. (왜 거품 같은지는 잘 모르겠다)

Transposition and Bubble Sort

그런데 이 bubble sort에서의 swap, 어디선가 많이 본 형태인 것 같다.
바로 우리가 위에서 계속 이야기했던 transposition(호환)이다!

(애초에 이름부터 trans + position, 위치를 바꾼다는 뜻이다)

즉, bubble sort의 과정 자체가 transposition들의 결합 형태로 표현이 가능하다는 것이다.

Conclusion

이렇게 됨으로써 우리는 결론에 도달할 수 있게 된다.

우리가 이 포스트를 거쳐 이야기했던 사실은 다음과 같다.

1. Sorting Algorithm은 임의의 집합을 non-decreasing order로 재배열하는 permutation을 찾는 과정이다.
2. 적어도 2개 이상의 원소를 갖는 유한집합의 모든 permutation은 transposition의 결합으로 표현이 가능하다.
3. Sorting의 종류 중 하나인 Bubble Sort의 swap 과정은 transposition의 형태이다.

즉, Sorting은 permutation을 찾는 과정이고, 이 permutation 또한 결국 크기 2짜리 cycle인 transposition의 결합으로 표현이 가능할 것이기 때문에, transposition의 형태인 원소쌍 간의 swap을 여러 번 거쳐 진행되는 Bubble Sort는 수학적으로 당연히 항상 올바른 결과를 만들 수 밖에 없다는 것이다!

마치며

사실 매우 간단해보이는 여러 알고리즘들이 왜 항상 성립하는가를 생각해보면, 왜 성립하는지를 쉽게 설명하지 못하는 경우가 꽤 많다.

물론 이렇게까지 엄밀하게 수학적으로 왜 성립하는지를 증명할 필요까지는 없겠지만, 여러 알고리즘을 공부하면서 단순히 외우기보다는

" 이 알고리즘은 왜 항상 모든 Input에 대해 성립할까? 혹시 예외는 없을까? "

를 고민해보는 과정도 중요한 과정이라는 생각을 하며 포스트를 마친다.