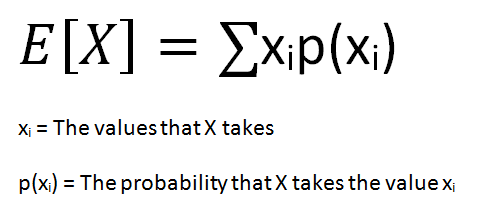
Random Variable
Random Variable이란?
특정 실험에서 각 결과가 가질 수 있는 Numerical Value(숫자로 나타낸 값) 이다.
그러니까 결과값, Random이 가질 수 있는 값들을 의미함.
2.1 Discrete Random Variable
이 결과값(Random Variable)이 연속적이지 않고 그냥 값을 가질 때.
어디부터 어디 사이의 값 이런거 말고 그냥 10, 20, 100 이렇게
- Probability Mass Function (pmf)
확률 질량 함수
( !! 확률이 discrete한 것이 아니다. State Space가 discrete 한 것! )
x가 어떤 값일때의 확률
State Space란? (상태 공간)
: 표본공간의 각 원소가 갖는 수치적인 특성을 나열한 것그러니까 주사위를 예로 든다면
Sample Space는 {1, 2, 3, 4, 5, 6}이 되겠지만
State Space는 주사위에서 -2를 한 값, 주사위를 던진 횟수 기타 등등 우리가 관심있어하는 값이 될 수 있다는 듯 하다.
교수님은 좀 혼용해서 쓰신 듯
- Cumulative Distribution Function (cdf)
누적 분포 함수
값이 x일 때까지의 누적 확률 값
누적이니까 점점 값 커질수록 값이 커진다. 값은 1을 넘을 수 없다.
2.2 Continuous Random Variable
확률 밀도 함수 : 주어진 변량이 정해진 구간 안에 존재할 확률
State Space가 Continuous한 경우이다.
값이 연속적이니까 그 확률값은 함수 f(x)로 표현!
- Probability Density Function (pdf)
f(x)가 State Space의 값을 가질 때를 적분 한 값이 1
그러니까 모든 확률 값의 합은 1이 된다.
모든 확률이 나올 값은 1이 되니까.
- Cumulative Distribution Function
x까지 가질 수 있는 값.
- -∞부터 x까지의 값을 적분하여 구한다.
P( a < X ≤ b ) = P(X ≤ b) - P(x ≤ a) = F(b) - F(a)
헷갈리니까 총 정리
| Discrete | Continuous | |
|---|---|---|
| x값 | 실수값 (10, 20, 100 ... ) | x |
| 확률 | pi | 연속이라 식으로 정의 (f(x)) |
| 확률값 | Probability Mass Function (pmf) | Probability Density Function (pdf) |
| 누적값 | Cumulative Distribution Function | Cumulative Distribution Function |
그래도 너무 헷갈린다... cdf는 똑같으니까 누적으로 이해하고 pmf는 알파벳이 뒤니까 앞, pdf는 알파벳이 앞이니까 뒤 이렇게 어거지로 외우는 중 ㅜㅜ
2.3 Espectation
기댓값 = 평균 (mean)
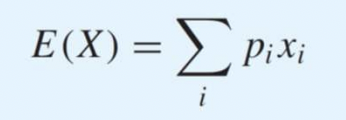
pi : 확률
xi : numerical value (숫자로 나타낸 값)
그러니까 쉽게 말해서 값 x와 그 x일 때의 확률값을 곱해서 전부 다 더해준다 그러면 평균값임.
만약 E(x^2) 을 구해야한다면 Xi^2만 해서 해준다. pi(확률값)는 그대로!

continuous한 경우 pi대신 f(x)를 넣고 전체 범위를 적분해서 기댓값을 구한다.
f(x)는 확률값이기 때문에 E(X)의 X가 변해도 f(x)의 값은 변하지 않는다.
한 마디로 f(x)는 값 x가 될 확률값이다 그러니까 둘을 곱하면 (discrete할 때와 동일) 그 때의 평균값이 나오는데 그걸 다 더한다 -> 적분한다 그렇게 보면 될 듯. continuous하니까 하나하나 다 더할 수는 없잖아.
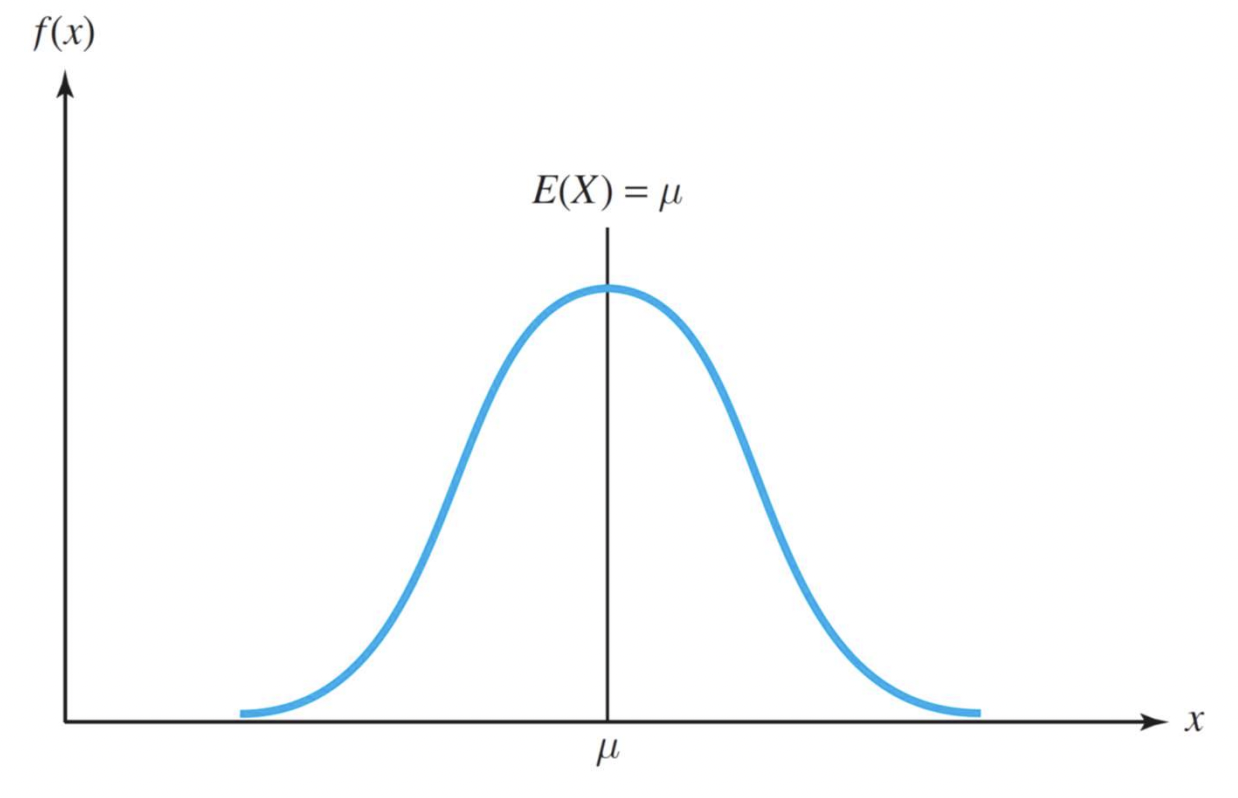
Symmetric Random Varialbes : 좌우 대칭
Probability Density Function일 때 (continuous 확률값)
f(μ + x) = f(μ - x) 만족시 기준점(대칭점) μ 를 기준으로 좌우대칭이다.
Random Variabale = g(X)일 때
E(x) -> E(g(X))로 변하는 것이기 때문에
x값만 g(X)로 바꾸어주면 된다. 확률값은 바뀌지 않는다!!
Median 중간값
Cumulative Distribution Function F(x)일 때,
F(x) = 0.5
그러니까
확률적으로 가운데의 그 때 x값이 궁금하다는 뜻.
반에서 중간인 애의 점수(점수 평균값이랑 다르다)
Symmetric Random Variables
대칭인 경우에는 Median(중간값) = Mean(평균)
2.4 Variance
분산이 뭐냐?
평균에서 떨어진 정도를 의미한다. 반대로 말하면 평균에 얼마나 모여있는가.
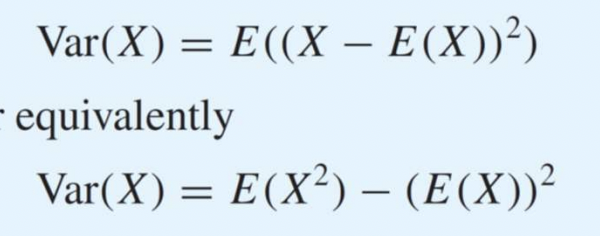
두 식은 동일하다. 편할대로 쓰면 됨.
표준편차는 분산에 루트한 절댓값.
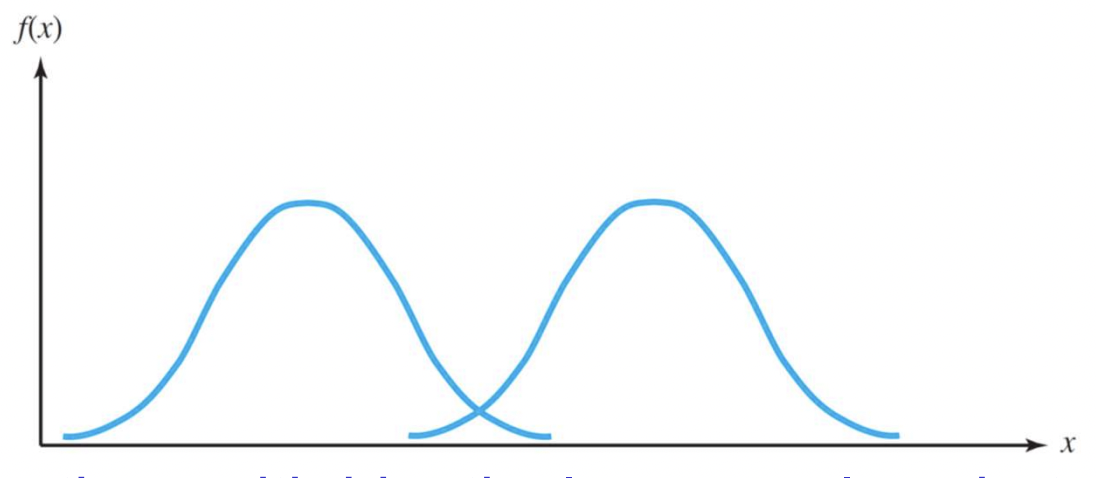
- 분산은 같지만 평균이 다른 경우
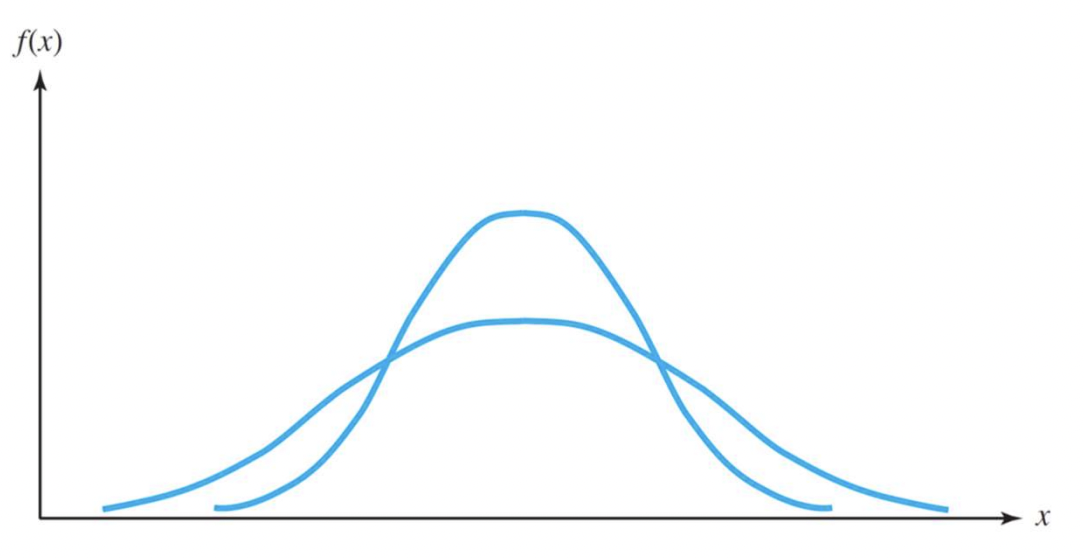
- 분산은 다르지만 평균은 같은 경우
Chebyshev's Inequality
교수님이 별도로 공부하라고 강조했던 그 친구!!
어떤 f(x)가 존재하더라도 무조건 만족한다.
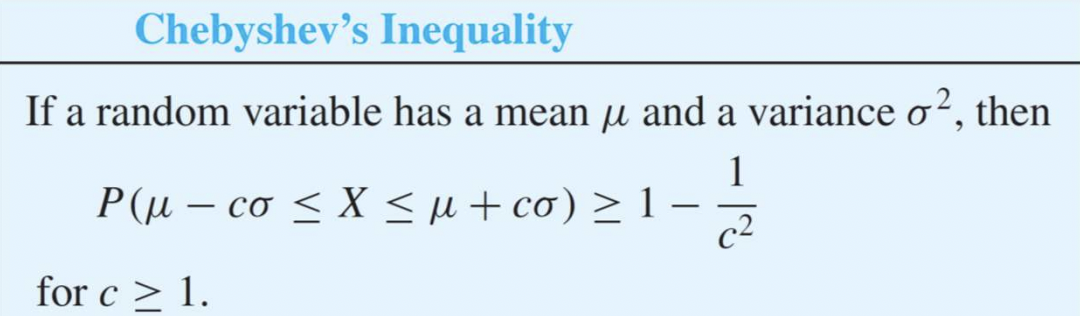
평균값을 중심으로 똑같이 μ만큼 떨어지면 그 값은 1 - 1/(c^2)보다 무조건 크다는 뜻이다. 그러니까 반대로 말하면 그래프의 해당 범위에서의 최소값을 구해낼 수 있다는 뜻.
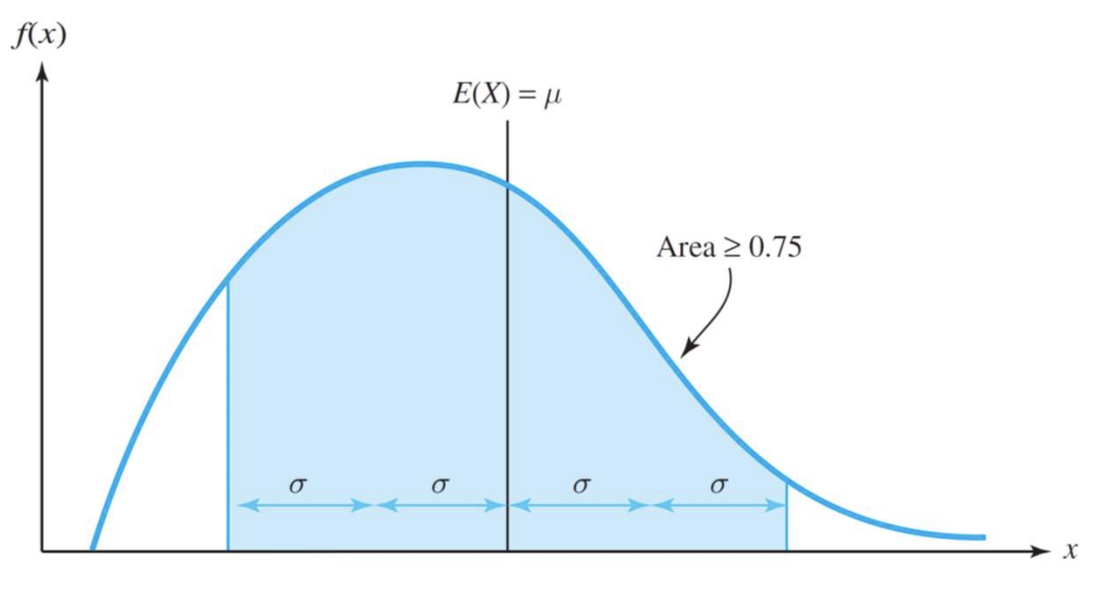
- c = 2 일 때, 0.75
- c = 3 일 때, 0.89
c = 1 일때는 면적은 0보다 크거나 같다. 당연하다.
그리고 전부 누적하면 면적 = 확률이기 때문에 1이 되겠지.
이걸 사용해서 최소 75%일 때의 값의 범위 값을 구해낼 수도 있다.
필요한 것이 평균과 표준 편차 뿐만이므로 실제 분포를 알지 않고 도출이 가능하다.
Quantiles 분위
F(x) = p
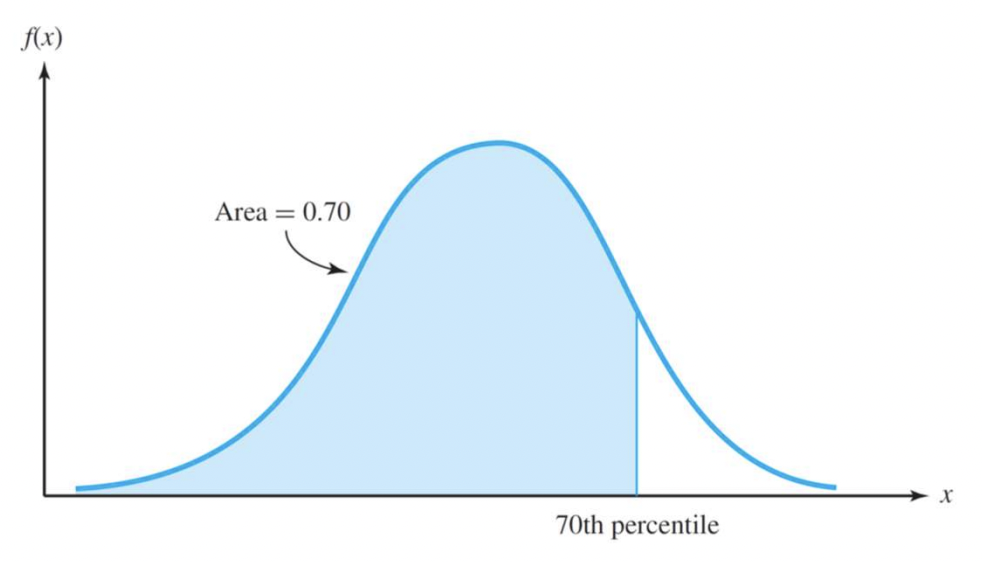
25%, 75% ... 이렇게 해당 범위를 찾고, 그 범위일 때의 x값을 찾는다.
Quartile
- Upper Quartile : 75%일 때의 분포
- Lower Quartile : 25%일 떄의 분포
- Interquartile range : 두 개의 Quartiles 사이의 거리
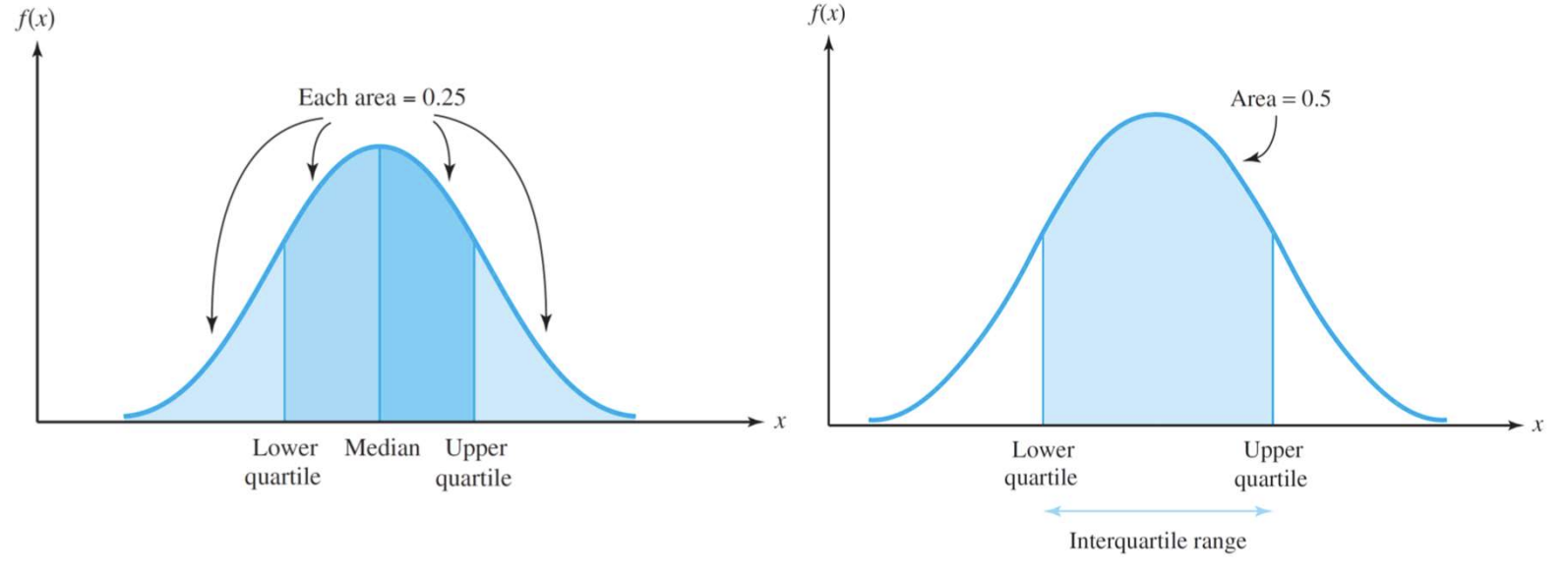
F(x) = 0.5 일 때의 x 값 = Median
항상 이 때의 x 값을 구하는 걸 잊지 말기
2.5 Jointly Distributed Random Variable
Random Variable이 2개인 경우 (X, Y)
- Joint Probability Mass Function
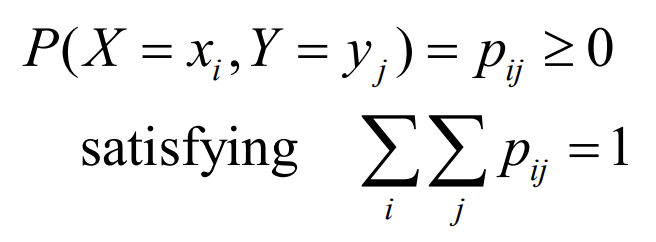
Random Valuable 이 x, y 두 개고 확률 값은 0 이상으로 이미 주어졌다,
그럴 때 확률 값들의 합이 1을 만족한다.
그리고 여기서
Q) Pij가 뭐냐?
A) i이고 j일 때의 확률 값이다.
- Joint Cumulative Distribution Function
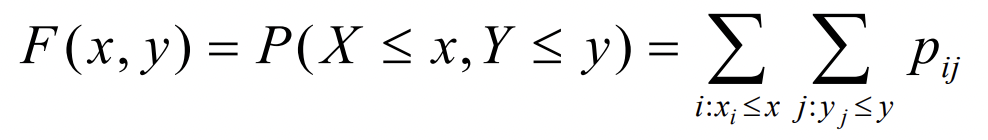
P에서 X, Y의 범위는 ≤ 이다. = 이 아님을 명심하기. 누적값이니까.
- Joint Probability Density Function
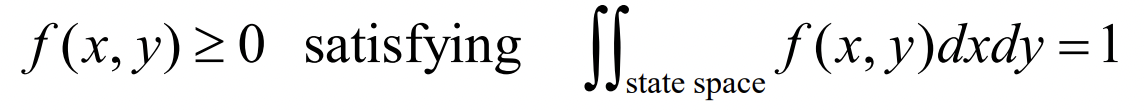
x에 대해 알고싶으면 y를 구하면 되니까 fx(x) = ∫ f(x,y)dy 를 구해주면 된다.
- Joint Cumulative Distribution Function
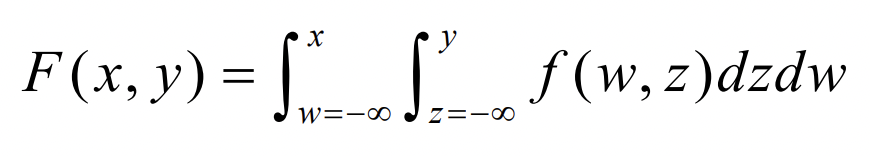
Joint CDF 한마디로
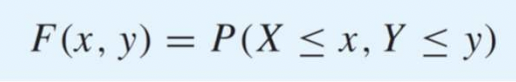
라고 정리해서 볼 수 있다.
Marginal Probability Distribution
주변 확률 분포
확률 분포이긴한데, 값 하나만 만족할 때를 구하는거다.
X1 일 때가 궁금하면 X1일 때의 Y 값을 다 더하고, Y1일 때는 그 반대로.
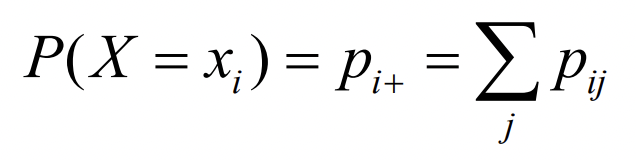
- p.d.f 일 때는 이렇게 구한다.
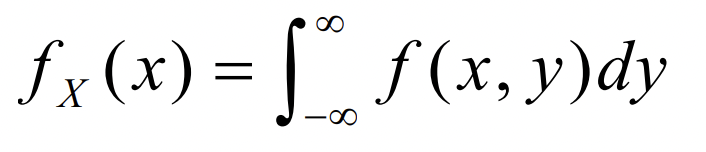
fx(x)라고 x를 따로 명시한다. 적분은 y에 대해서 한다. 이러면 바로 X에 대해서 구하기가 가능. 물론 fy(x)도 가능하다. 이러면 y에 대해서 궁금할때겠지?
Conditional Probability Distribution
조건부 확률 분포
Conditional이 붙으면서 세계관을 좁혀준다? 이렇게 봐도 좋을 듯.
그래서 전체적으로 Sample Space가 그대로일 때 보다 값이 커지게 된다.
Joint로 된 것(X, Y 같이)을 알고 있을 때, Marginal Condition(값 하나만 만족할 때)을 따로 구해주어야한다.

Y = yj 이면서 그 때를 만족하는 x의 확률 값들의 합을 구한다고 보면 된다.
아래 식은 풀어서 설명한 것.
전체 fy일 경우에서, fy이면서 fx일 때의 확률 값을 구한 것이다.
Independent Random Variable
X와 Y가 독립적이다. (연관관계가 없다는 뜻임. 교집합이 없다는 뜻 아님)
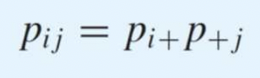

사실 이걸 더 많이 쓴다 그냥 둘 곱해라.
Covariance
두 개의 변수 사이의 관계 (dependency) - 두 변수의 관계를 나타내는 양
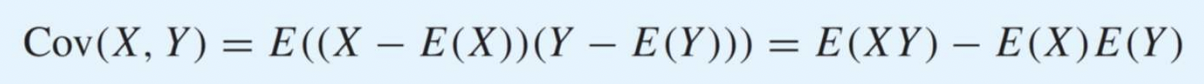
그러니까 (X 평균에서 떨어진 값) (Y 평균에서 떨어진 값)
대충 거리 거리 라고 보면 되겠다.
Cov 값 = 0 이면 둘 사이의 관계가 없다는 뜻이 된다.
Correlation
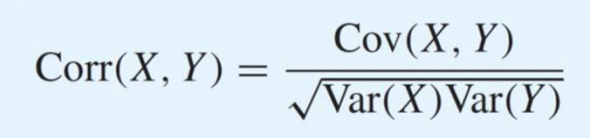
-1과 1 사이의 값만 가진다.
- 그래서 둘 차이점이 뭔데?
Cov는 관계가 있는지 없는지만 알 수 있다.
+, -, 0 3가지만 알 수 있다. 모든 값을 가질 수 있다. 그래서 값이랑 별 상관은 없다. 그냥 0이면 관계가 없다 이 정도만 알 수 있는 것.
Corr는 relationship이 강한지 약한지를 볼 수 있다.
-1 ~ 1 사이의 값만 가질 수 있다. 수가 크면 더 끈끈하다.
그렇다고 한다. 사실 확실하지는 않음. 인터넷 열심히 보고 유튜브도 열심히 봤는데 내가 도출한 결론은 이것임... ㅜㅜ 어렵다.
2.6 Combinations and Functions of Random Variables
Linear Function of a Random Variable
Linear Function은 일반적인 결과치를 의미하는 듯 하다. Combination

고등학생때도 했던 것 같다 응... 대충 보고 넘어가자.
근데 교수님이 예제 문제를 많이 내신 거 보면 꼭 기억은 해야할 듯 .
Sum of Random Variables

평균은 그냥 더하고,
분산은 dependency(Cov)를 체크하자. 만약에 독립적이면 그냥 더해도 좋다.
선형의 경우
선형 : Y = a1X1 + a2X2 + ... + b 의 형태
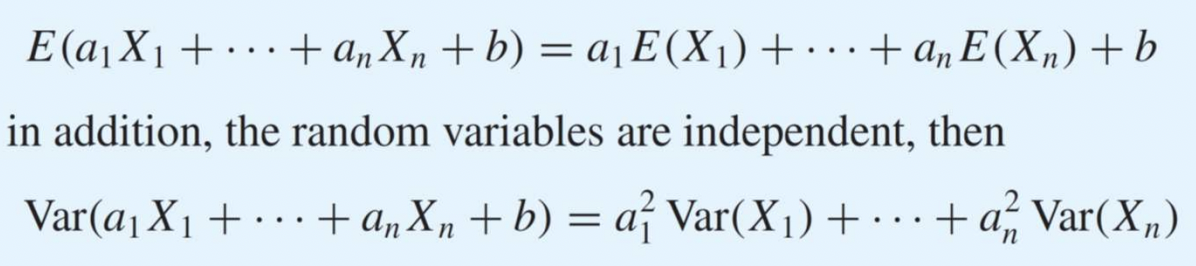
여기서 분산이 independent 한 경우만 적어둔 이유는, 만약 독립적이지 않으면 Cov를 엄청 더해줘야한다. 완전 값 더러움. 그래서 주로 독립적인 경우를 취급한다.
Averaging Independent Random Variables
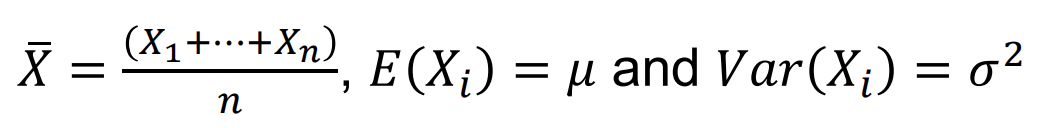
일 때, 독립적인 Random Variables을 평균화
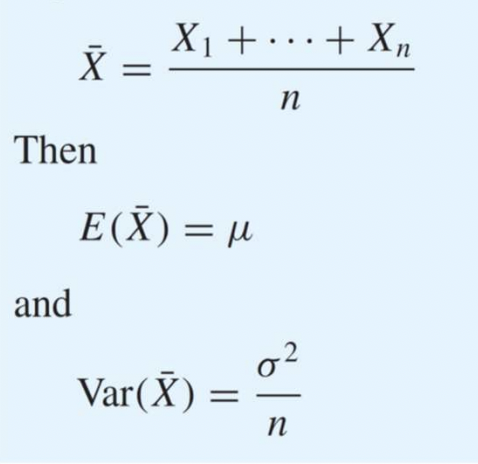
평균의 경우, 그냥 E(x) = ax + b니까 값이 그대로가 된다. 그냥 1/n 한 걸 n 번 더한 것과 같으니까.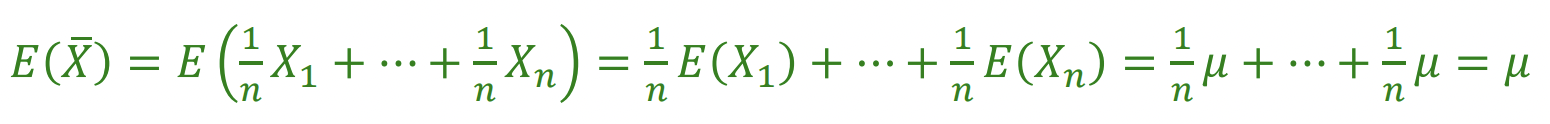
분산의 경우, Var(x) = a^2X이므로 전개해서 풀어주면 저렇게 1/n을 곱한 값이 도출된다.
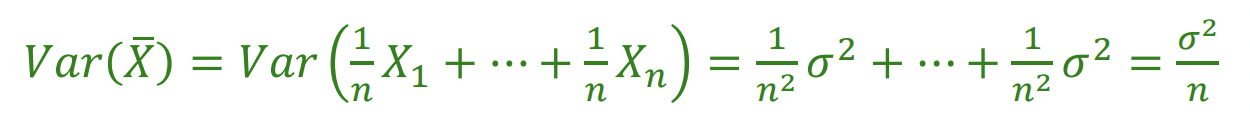
평균은 그대로, 분산은 주는 그러한 형태를 보인다.
Nonlinear Functions of a Random Variable
일반적인 결과치가 아닐 때(Nonlinear) 관계를 찾는다.
그러니까 X와 Y 사이의 관계를 정의하기 어려울 때 관계를 만들어준다.
Y = (X에 대한 식)의 형태일 때
X의 cdf로부터 Y의 cdf를 만든다.
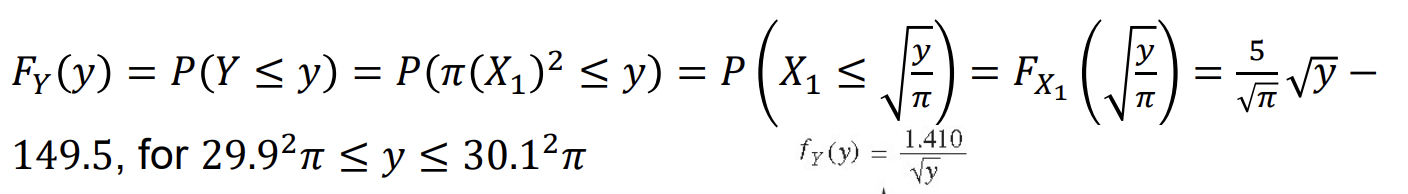
이렇게 Y에 관한 cdf가 정의되어 있을 때,
1️⃣ Y를 식을 통해 정의된 x에 대하여 바꾸고
2️⃣ 그걸 x에 대한 식으로 정리해서 y에 관한 식을 만들어낸다!
