[모두를 위한 선형대수학] 1. 벡터(Vector)

1. Vector의 정의

• Vector : 크기와 방향을 동시에 나타내는 것
  - Ex : 시속 5마일과 동쪽의 정보가 합쳐지면 vector가 되며, 이 값은 속력이 아닌 속도
• Scalar : 어떤 물체가 시속 5마일로 이동하는 것은 vector가 아닌 단지 크기

2. 실좌표공간

$R^2$ : 2차원 실수좌표공간

---

• 2차원 실수좌표공간 가능한 모든 실수값을 가지는 2-튜플
• 숫자 2개인 순서 리스트이자 실수 2개의 순서 리스트
• $R^2$를 다룬다는 것은 모든 가능한 실수값을 가지는 2-튜플을 다루는 것
• 따라서 이 공간 위 모든 벡터들이 어디에 있는지 알 수 있으며, 각 성분들은 실수로 이루어져 있음
  - Ex : (3, 4) and (-3, -4)
• 크기는 없고 방향은 정해지지 않은 영벡터를 포함한 모든 2-튜플에 대해,
  이 벡터들을 조합하여 2차원 실수좌표공간 생성 가능

$R^3$ : 3차원 실수좌표공간

---

• 3차원 실수좌표공간 가능한 모든 실수값을 가지는 3-튜플
• $\vec x$와 $\vec b$는 $R^3$라는 집합의 원소지만, 허수 성분을 가진 벡터, $R^2$와 같은 다른 차원에 존재하는 벡터는 $R^3$가 아님
  - [i 0 1] → 더 이상 실수 값을 가지는 3-튜플이 있을 수 없음

$R^n$ : n차원 실수좌표공간

---

• 1~100튜플까지 시각화 하는 것은 어려우나, 수학적으로는 표현 가능
• n-튜플 벡터로 표현

3. 대수와 그래프를 이용한 벡터의 덧셈

$\vec a+ \vec b = \vec b + \vec a$

• 2차원 벡터 두개의 합은 2차원 벡터 $R^2$
• 순서를 바꾸어도 덧셈의 연산 결과는 같음

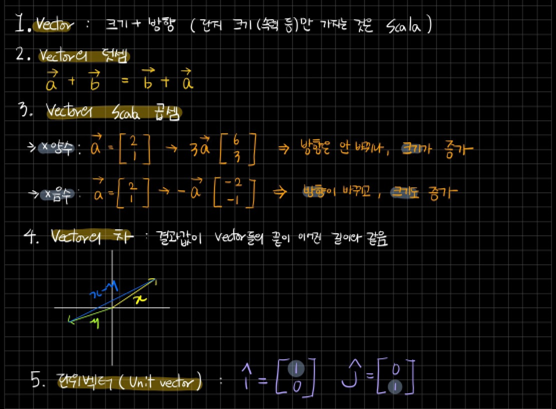
4. 벡터의 스칼라 곱셈

• 벡터 a에 스칼라 +3을 곱하면,
  • 방향이 바뀌지 않지만, 크기는 증가 (스칼라의 어원 : scale)
  • $a = {2\brack1} → 3a = 3{2\brack1} ={6\brack3} ~a$

• 백터 a에 스칼라 -1을 곱하면,
  • 방향이 완전히 반대가 되지만, 크기는 변하지 않음

• 백터 a에 스칼라 -2를 곱하면,
  • 방향이 바뀌고 크기 2배 증가
  • $a = {2\brack1} → -2a = -2{2\brack1} ={-4\brack-2}$

5. 벡터의 차

하기 그래프에서 알 수 있듯이, 결과 값이 벡터들의 끝이 이어진 길이와 같은 것을 알 수 있음

• $X-Y =X+-1Y$
• $X{2 \brack 4}, Y{-1 \brack-2} → X-Y = {2 \brack4} +{-1 \cdot -1\brack -1 \cdot -2}={3 \brack6}$
  

6. 단위벡터 (Unit Vector)

• 열벡터 = ${1 \brack7}$
• 단위벡터 = $i+7j$

7. 직선의 매개변수 표현

$S= \lbrace c\vec v | c \in R \}$

• S = 동일선상에 존재하는 벡터의 집합
• y=mx+b와 같은 기울기로 쉽게 표현할 수 있으나, 이와 같이 표현하는 이유는 3차원 이상을 표현하기 위함

1강. 요약정리