[Algorithm] Insertion Sort

1. Sorting Algorithm이란?

정렬 알고리즘은 n개의 숫자가 입력으로 주어졌을 때
이를 사용자가 지정한 기준에 맞게 정렬하여 출력하는 알고리즘

• Input : A sequence of n numbers <$a_1, a_2, ... , a_n$>
• Output : A permutation(reordering) <$a'_1, a'_2, ... , a'_n$> of the input sequence such that $a'_1 \leq a'_2\leq ... \leq a'_n$

2. Intuition of Insertion Sort

1. 처음에는 배열의 첫 번째 요소는 이미 정렬되어 있다고 가정한다.
2. 두 번째 요소부터 시작하여, 현재 요소를 정렬된 부분의 적절한 위치에 삽입한다.
3. 이를 위해, 현재 요소보다 큰 값들을 오른쪽으로 한 칸씩 이동시키면서, 적절한 위치를 찾으면 삽입한다.
4. 이 과정을 배열 끝까지 반복하면 정렬이 완료된다.
   

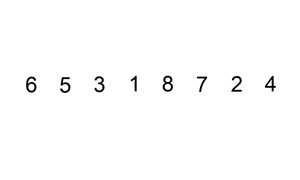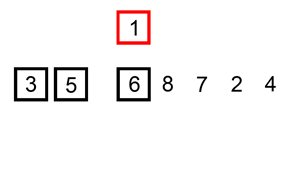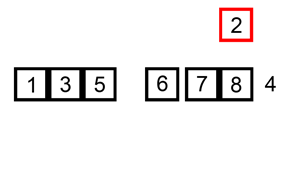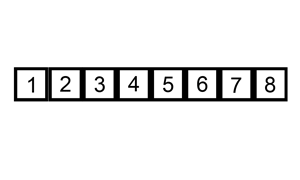
INSRTION-SORT(A)
	for j = 2 to A.length
    key = A[j]
    // Insert A[j] into the sorted sequence A[1..j-1]
    i = j-1
    while i>0 and A[i] > key
    	A[i+1] = A[i]
        i = i-1
    A[i+1] = key

3. Proving Correctness

루프 불변성(Loop Invariant)이란?

루프 불변성(Loop Invarient)이란 반복문이 실행될 때마다 항상 참(True)인 조건을 의미한다.
이 개념은 정렬 알고리즘의 정확성을 증명할 때 유용하게 사용한다.

• Insertion Sort에서 j에서 반복을 시작할 때 부분리스트인 A[1...j-1]은 항상 정렬되어 있다.

알고리즘의 정당성을 위한 3단계

• Initialization : 반복문이 시작되기 전에 불변성이 성립해야 한다.
  Ex) i = 1일 때, 부분 배열 A[0]은 길이가 1이므로 이미 정렬되어 있다 즉, 루프 불변성이 성립한다.
• Maintenance : 각 반복마다 불변성이 유지되는지 확인해야 한다.
  Ex) A[i]를 적절한 위치에 삽입하면, A[0]부터 A[i]까지도 정렬된 상태가 유지된다. 즉, 루프 불변성이 성립한다.
• Termination : 반복문이 종료될 때, 불변성을 통해 알고리즘을 보장할 수 있다.
  Ex) 루프 종료 조건 i = n이 되면, A[0]부터 A[n-1]까지 정렬되어 있으므로 따라서 A 전체가 정렬되었음을 보장할 수 있다.

4. Is Insertion Sort Fast?

The time of Insertion Sort

• times은 코드에서 최대로 실행될 수 있는 횟수이다.
• 단일 반복문은 n번, 이중 반복문은 단일 반복문 안에서 한번 더 반복하는 것이므로 $\displaystyle\sum$로 표현한다.
• 반복문 안에 명령어들은 조건이 False라면 실행을 하지 않으므로 n-1로 표현한다.