[알고리즘 정리] 기본 정렬 알고리즘

자바를 다시 시작하면서 기본 알고리즘들에 대해 리마인드 겸 정리를 해보고자 하였다.
(시작 인덱스는 자바에서 배열이 인덱스 0부터 시작한다고 가정하고 작성하였습니다.)

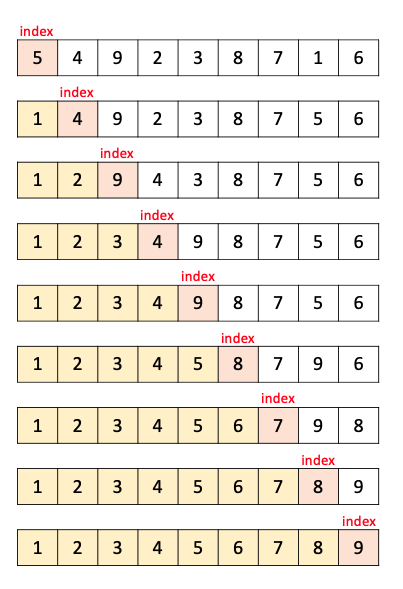
1. 선택 정렬(Selection Sort)

• 시간 복잡도: O(N^2)
• 공간 복잡도: O(N)
• 기본 로직
  1. 배열의 맨 앞부터 시작(시작 시 현재 인덱스=0)
  2. 배열의 정렬되지 않은 부분에서 가장 작은 값을 찾음
  3. 가장 작은 값을 찾으면, 현재 인덱스의 값과 교환
  4. 다음 인덱스에서 위 과정 반복
  

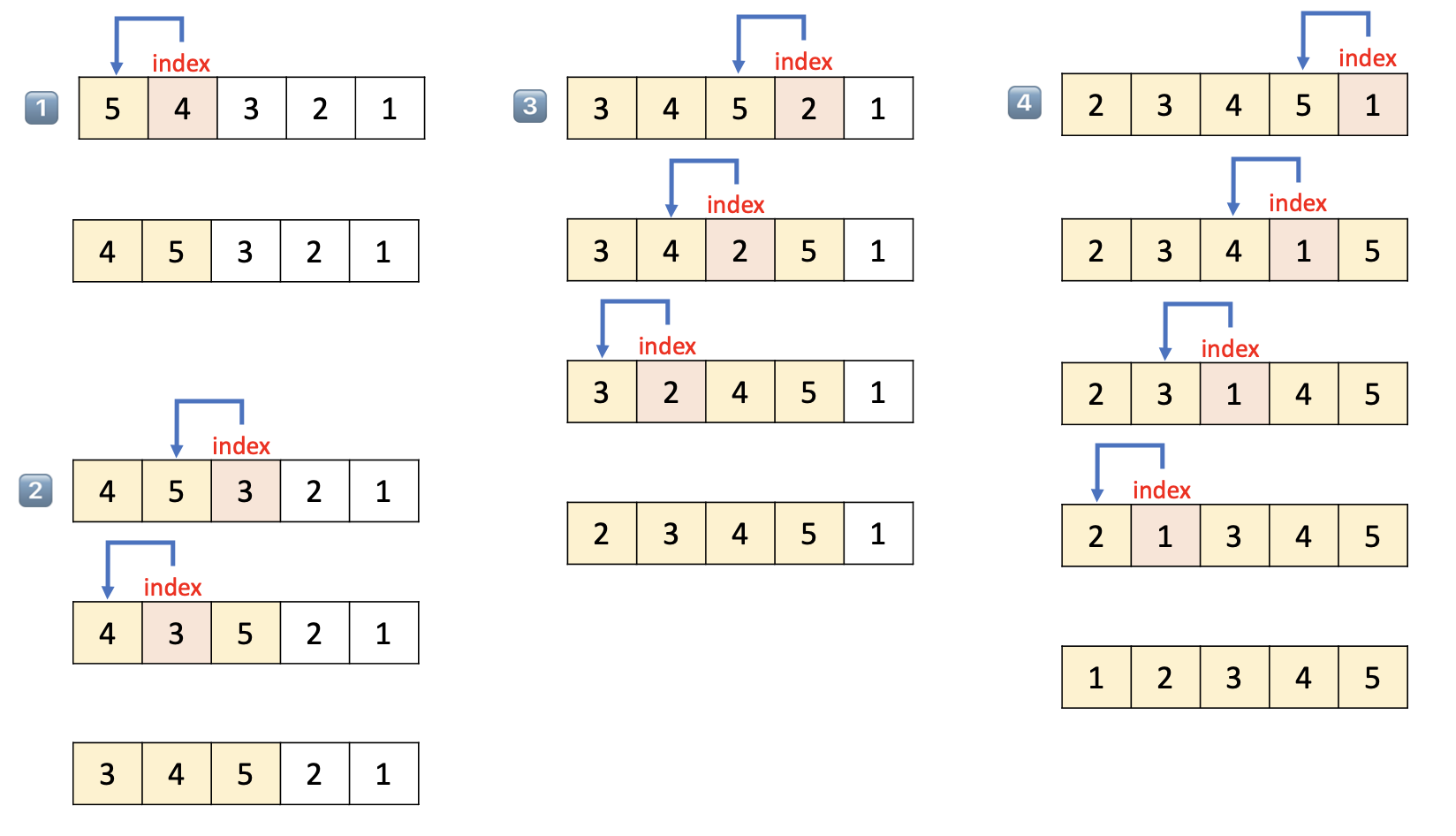
2. 삽입 정렬(Insertion Sort)

• 시간 복잡도: 최선 O(N^2) / 최악 O(N^2)
• 공간 복잡도: O(N)
• 기본 로직
  1. 배열의 2번째부터 시작(시작 시 현재 인덱스=1)
  2. 현재 인덱스의 값과 이전 인덱스(=현재 인덱스-1)의 값 비교
  3. 현재 인덱스의 값 < 이전 인덱스의 값 ⇒ 위치 교환 및 현재 인덱스=-1
  4. 다음 인덱스에서 위 과정 반복
  

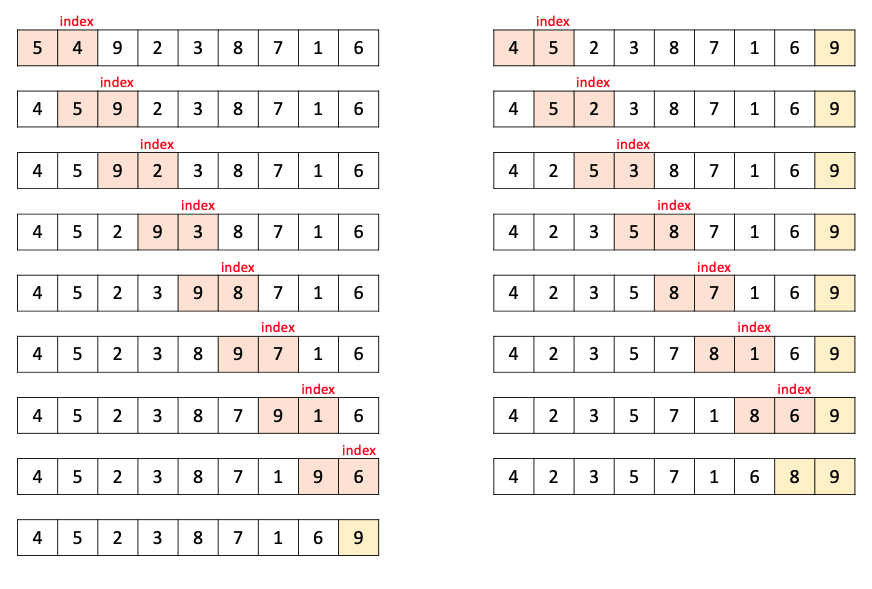
3. 버블 정렬(Bubble Sort)

• 시간 복잡도: 최선 O(N) / 최악 O(N^2)
• 공간 복잡도: O(N)
• 기본 로직
  1. 배열의 2번째부터 시작(시작 시 현재 인덱스=1)
  2. 현재 인덱스의 값과 이전 인덱스(=현재 인덱스-1)의 값 비교
  3. 현재 인덱스의 값 < 이전 인덱스의 값 ⇒ 위치 교환
  4. 현재 인덱스의 값 > 이전 인덱스의 값 ⇒ 교환하지 않고, 다음 연속 두 인덱스 값 비교로 넘어가 위 과정 반복
  

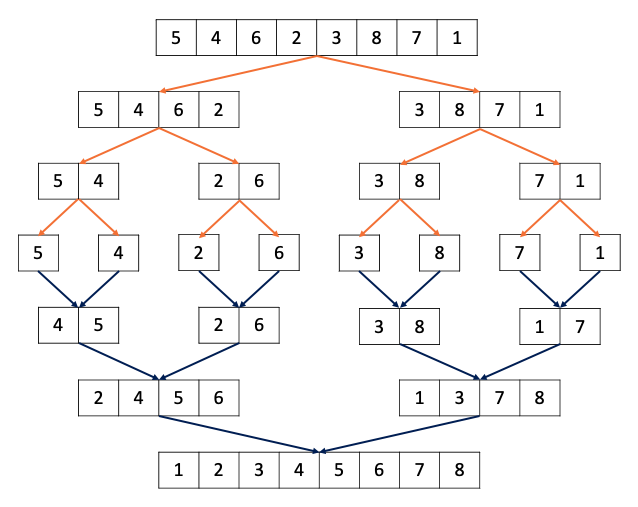
4. 합병 정렬(Merge Sort)

• 시간 복잡도: O(NlogN)
• 공간 복잡도: O(2N)
• 기본 로직
  • 분할(divide) 과정
    1. 현재 배열을 반으로 쪼개기
       • mid = (시작위치 + 종료위치)/2
       • 쪼갠 배열은 A(시작위치, mid)와 B(mid+1, 종료위치)
    2. 배열의 크기가 0이나 1일때까지 반복하여 쪼개기
  • 병합(conquer) 과정
    1. 두 배열 A, B의 현재 인덱스를 각각 i, j라 가정
    2. i, j에는 각각의 인덱스를 저장(처음에는 둘다 0 저장)
    - i = A 배열의 시작 인덱스
    - j = B 배열의 시작 인덱스
    3. A[i]와 B[j] 비교 → 둘 중 작은 값을 새 배열 C에 저장
    - A[i] < B[j] ⇒ C에 A[i] 저장. i++
    - A[i] > B[j] ⇒ C에 B[j] 저장. j++
    4. i, j 둘 중 하나가 각 배열의 종료 인덱스에 도달할 때까지 반복
    5. 끝까지 저장 못한 배열의 값을 순서대로 C에 저장
    6. C 배열을 원래 배열에 저장 후 완료
    

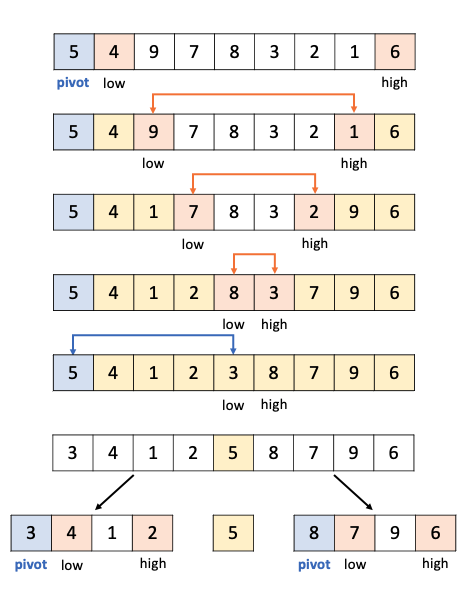
5. 퀵 정렬(Quick Sort)

• 시간 복잡도: 최선 O(NlogN) / 최악 O(N^2)
• 공간 복잡도: O(N^2)
• pivot point가 존재
• 기본 로직
  1. pivot point 설정(맨 앞 or 맨 뒤 or 중간 값 or 랜덤 값)
  2. 인덱스 지정
  - 배열의 가장 왼쪽 값의 인덱스=low
  - 배열의 가장 오른쪽 값의 인덱스=high
  3. 탐색
  - low는 오른쪽으로 탐색해가다 pivot 보다 큰 값이 있으면 멈춤
  - high는 왼쪽으로 탐색해가다 pivot 보다 작은 값이 있으면 멈춤
  4. 멈춰있는 상태에서의 low와 high 값 위치를 바꿔줌
  5. 3,4,5 과정을 low와 high가 만날때까지 반복
  6. 위 과정 끝나면 low와 pivot 값을 바꿔줌
  7. 두 배열로 나눠 다시 위 과정 반복(여기서 low는 6번에서의 low값)
  - 맨 왼쪽부터 low-1
  - low+1부터 맨 오른쪽까지
  

기본 정렬 알고리즘 관련 백준 문제

• Bubble Sort
  2750번 수 정렬하기(with. JAVA)