이번 블로그에서는 cs182 2강을 정리할 예정이다. 2강은 머신러닝에 대한 개괄적인 소개를 할 예정이며 특히 지도학습을 중점으로 loss function, optimization에 대해 간략하게 볼 예정이다.
해당 강의의 유튜브목록은 링크이며 해당 강의 사이트는 여기에서 찾을 수 있다.

2강

2.1 지도학습

2.1.1 지도학습/비지도학습/강화학습

머신러닝에는 크게 지도학습/비지도학습/강화학습으로 구성된다.

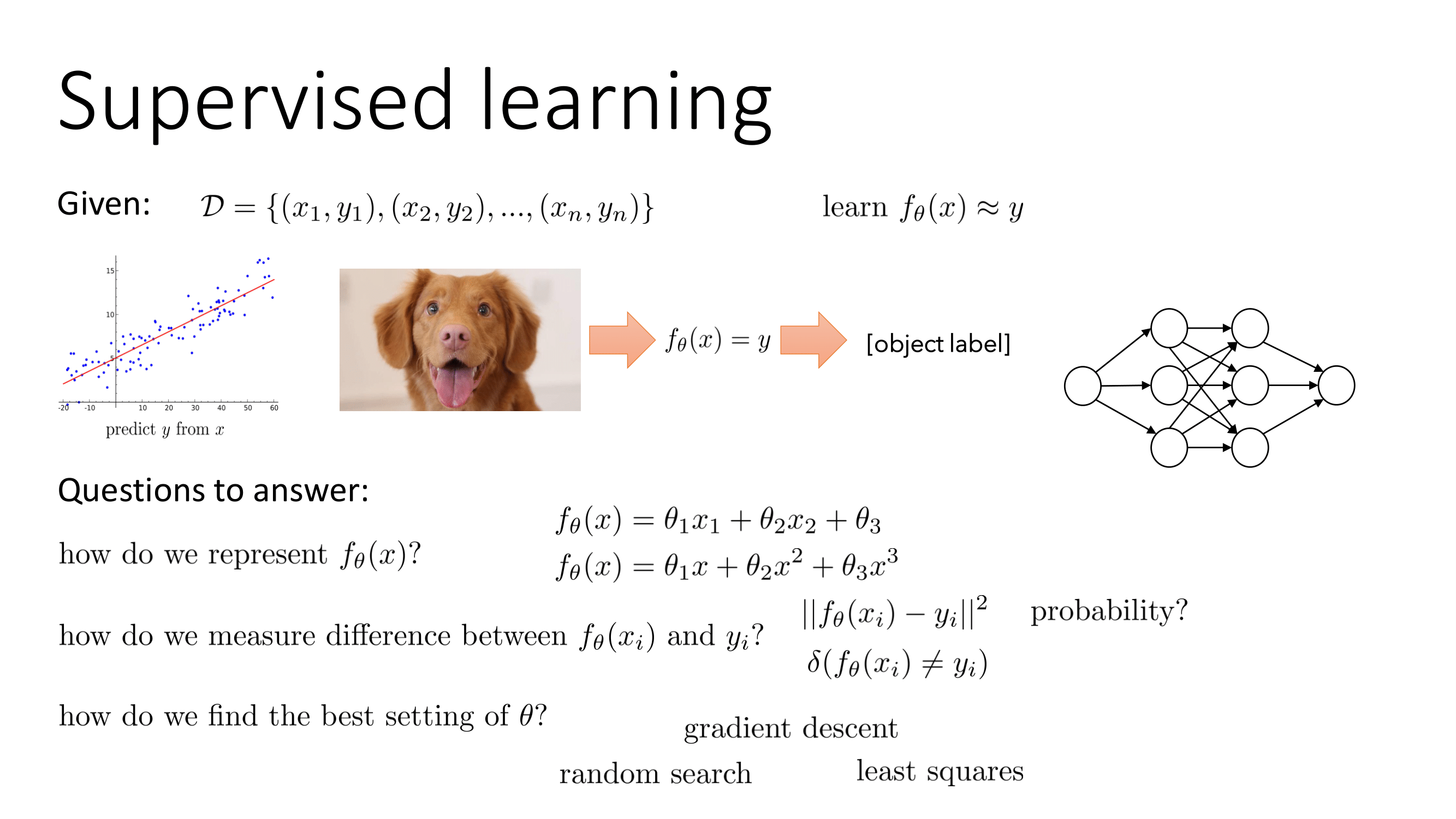
지도학습(Supervised Learning)이란 x,y로 구성된 데이터셋이 주어지고 x로부터 y를 예측하는 것을 의미한다. 이때 지도학습의 함수는 $f_\theta(x)=\theta_1x_1+\theta_2x_2+\theta_3$ 나 $f_\theta(x)=\theta_1x+\theta_2x^2+\theta_3x^3$로 표현가능하다. 지도학습의 결과와 실제 결과의 차이는 L1, L2와 같은 거리로도 측정가능하고 확률을 이용해서도 가능하다. 마지막으로 최적의 $\theta$는 random search, Least Square, gradient descent등으로 구할 수 있다.

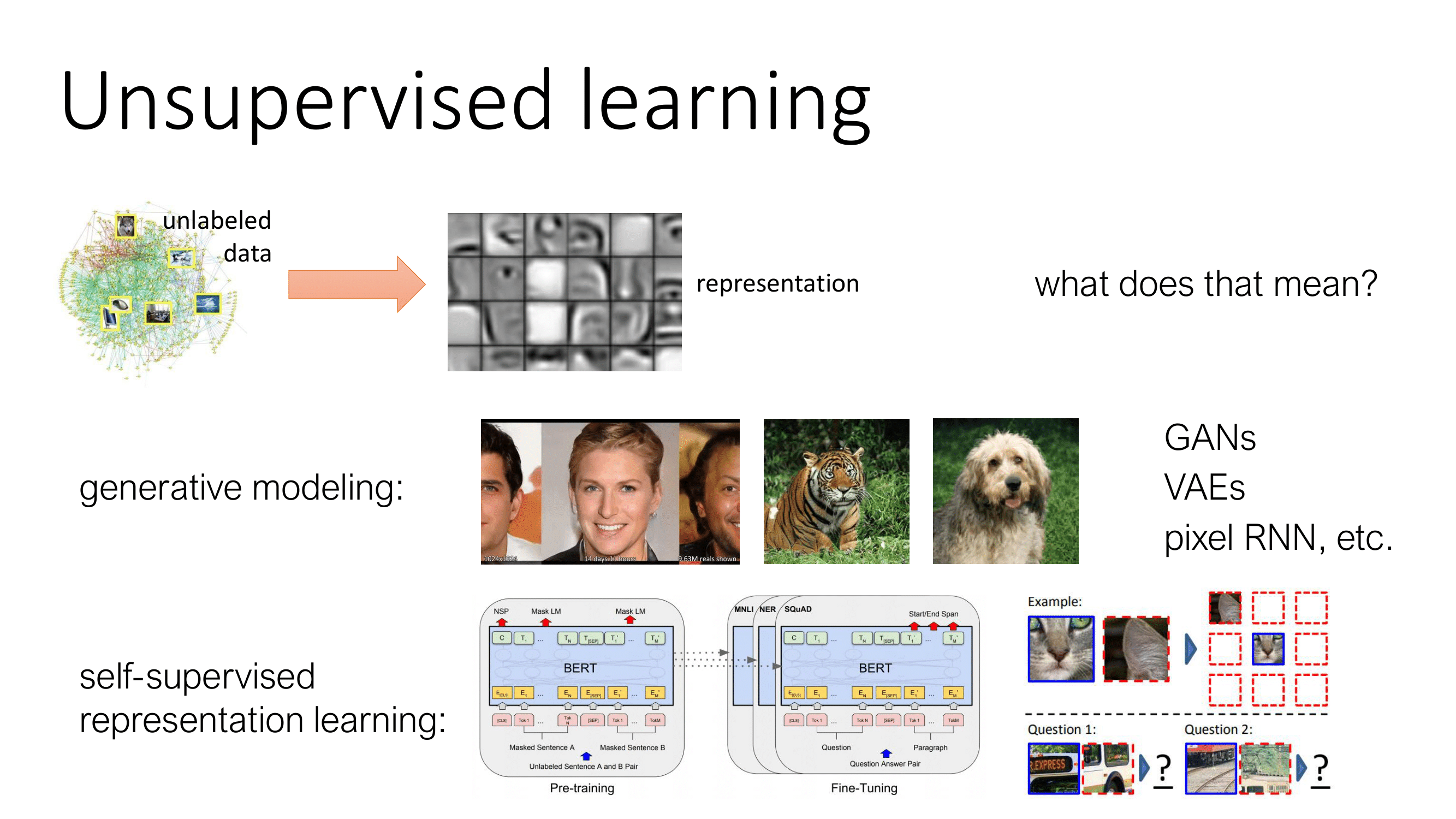
비지도학습(Unsupervised Learning)이란 unlabeled 데이터에서 representation을 구하는 학습이다. 대표적인 모델로 GAN, VAE와 같은 생성모델이 있으며 BERT, GPT와 같은 self-supervised representation learning이 있다.

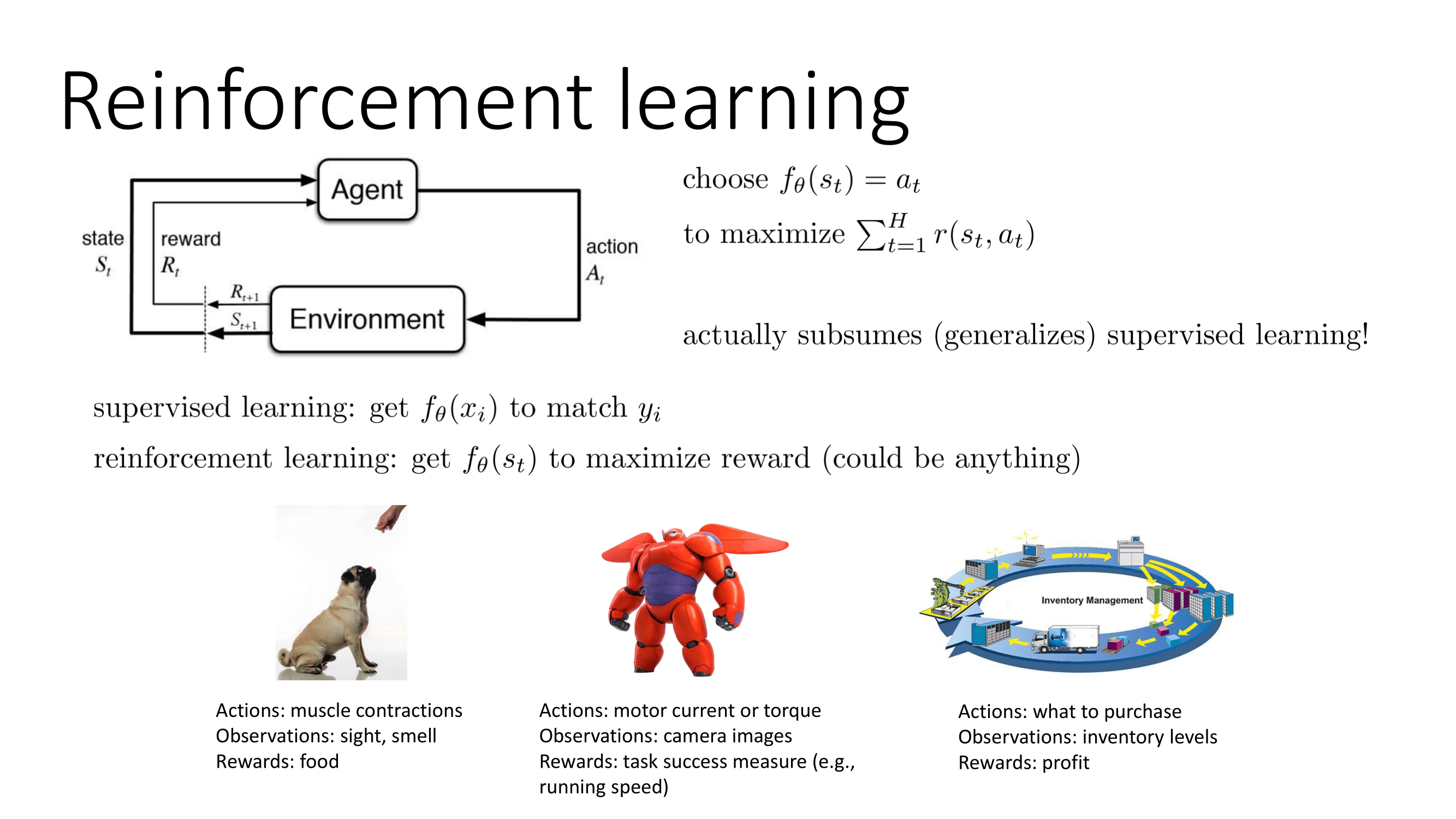
강화학습(Reinforcement Learning)이란 $\sum_{t=1}^Hr(s_t,a_t)$ 를 최대한으로 만드는 $f_\theta(s_t)=a_t$ 를 고르는 문제이다. Sergey Levine교수님은 지도학습은 어찌보면 강화학습의 일종이다라고 이야기했다.. 지도학습은 $y_i$를 맞추는 $f_\theta(x_i)$를 얻는 것이며 강화학습은 보상을 최대화하는 $f_\theta(s_t)$를 얻는 것이다. 즉 이떄 강화학습의 보상은 어떤것이 될 수 있기에 보상이 $y_i$라면 지도학습도 강화학습의 일종이 될 수 있다.

2.1.2 지도학습

이 셋중 가장 기초가 될 수 있는 지도학습부터 먼저 살펴보자.

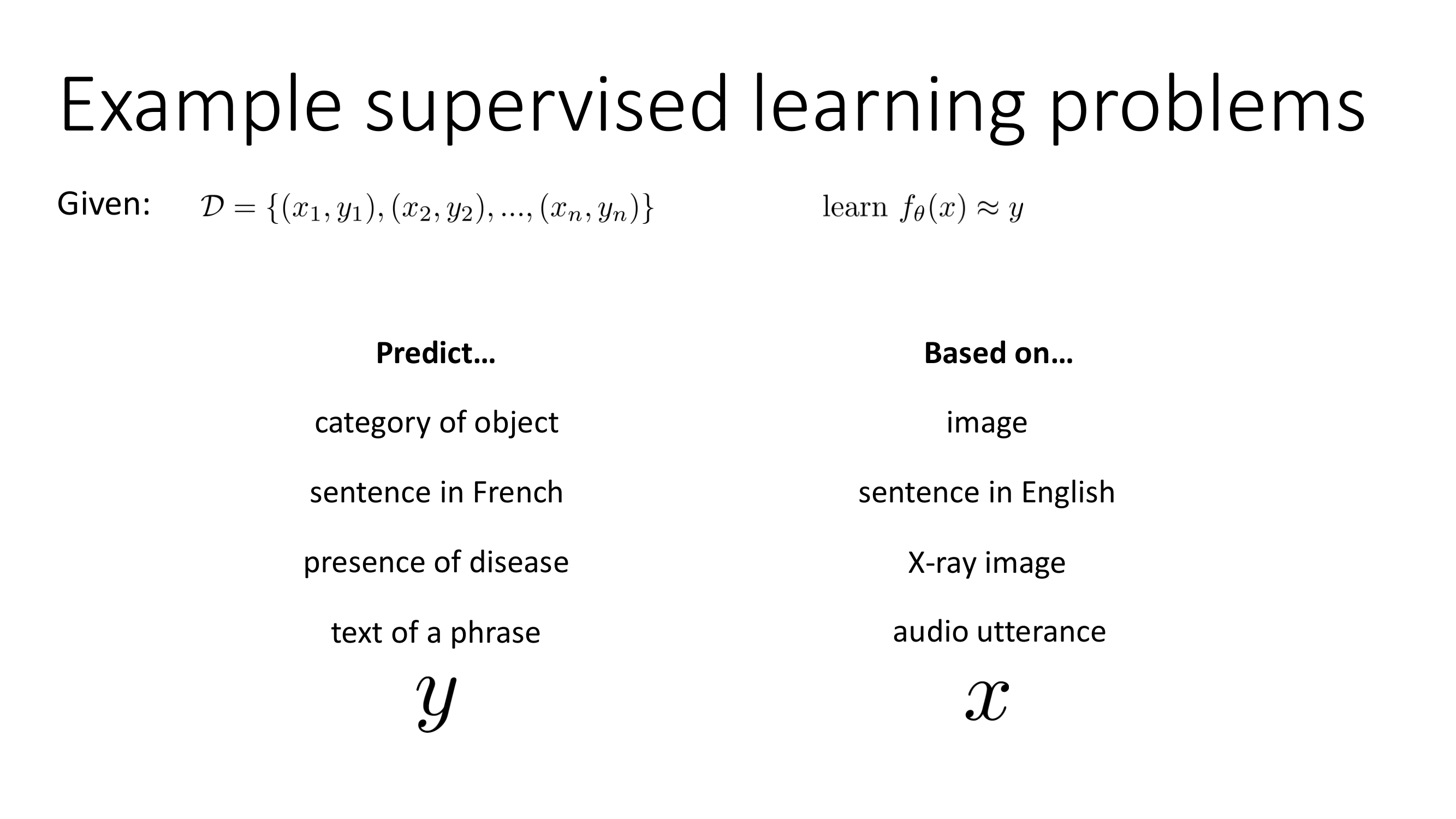
지도학습은 현재 산업에서 가장 많이 사용하고 있는 머신러닝이며 기업들에게 연 수십억 달러의 이익을 가져오고 있다. 지도학습은 image로부터 물체의 종류를 예측하기, 영어로 된 문장을 프랑스어로 바꾸기, x-ray image로부터 질병 유무 판단하기, 음성으로부터 텍스트 예측하기 등등이 있다.

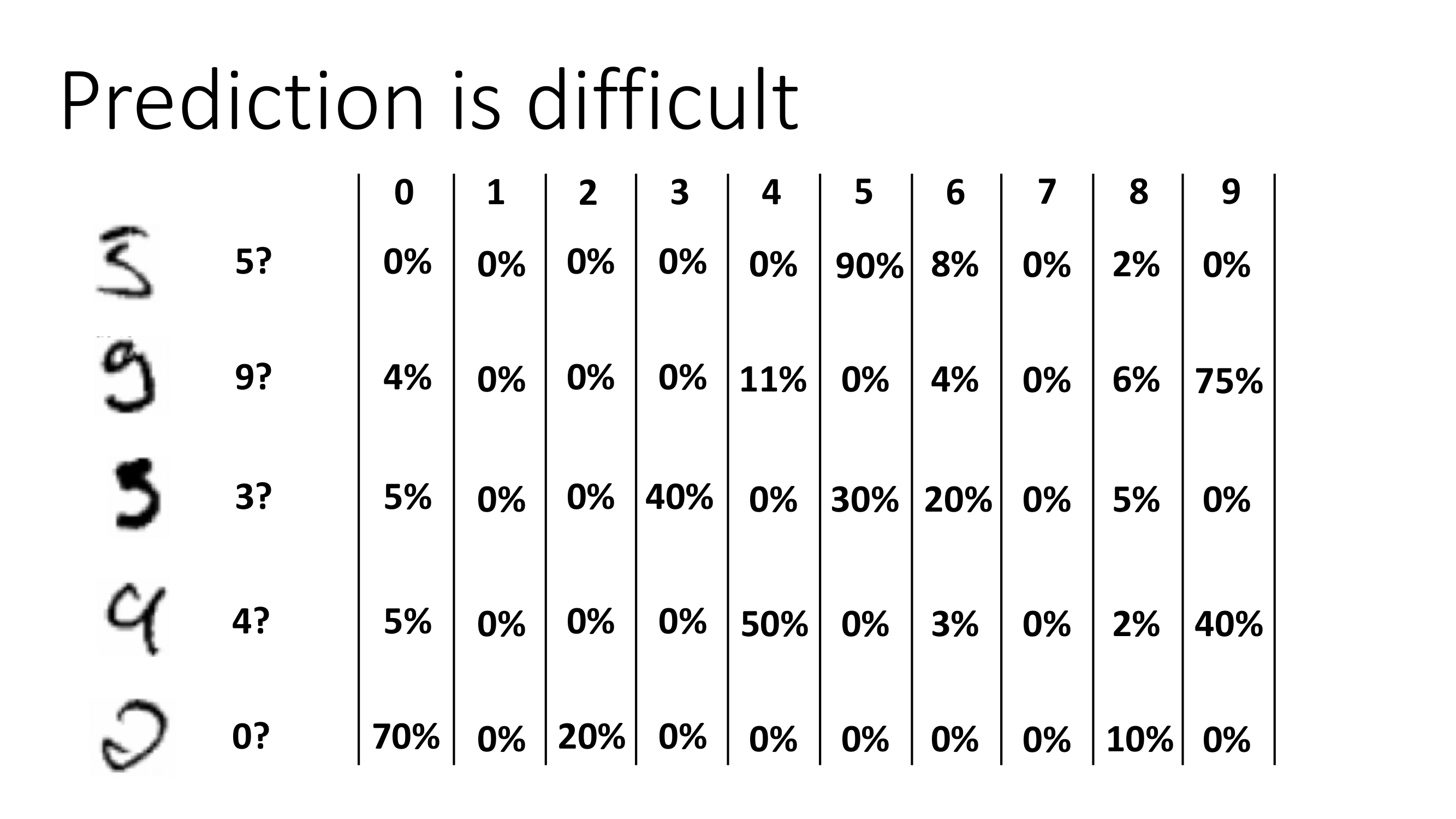
지도학습은 가장 기초적인 이론이긴 하지만 예측은 늘 어려운 영역에 속해 있다. MNIST의 예를 들면 첫번째 사진은 90% 확률로 5이며 8% 확률로 6이며 2%확률로 8이다. 이때 바로 결과값이 나오게 만들면 예측값 또한 확률값에 의해 그때그때마다 달라질 것이다. 그렇기에 지도학습에서 바로 $f_\theta(x)\approx y$가 아닌 조건부 확률 $p_\theta(y|x)$로 구해 확률값을 도출해 구한다. 그렇게 되면 다음과 같은 방식으로 지도학습이 변화한다.

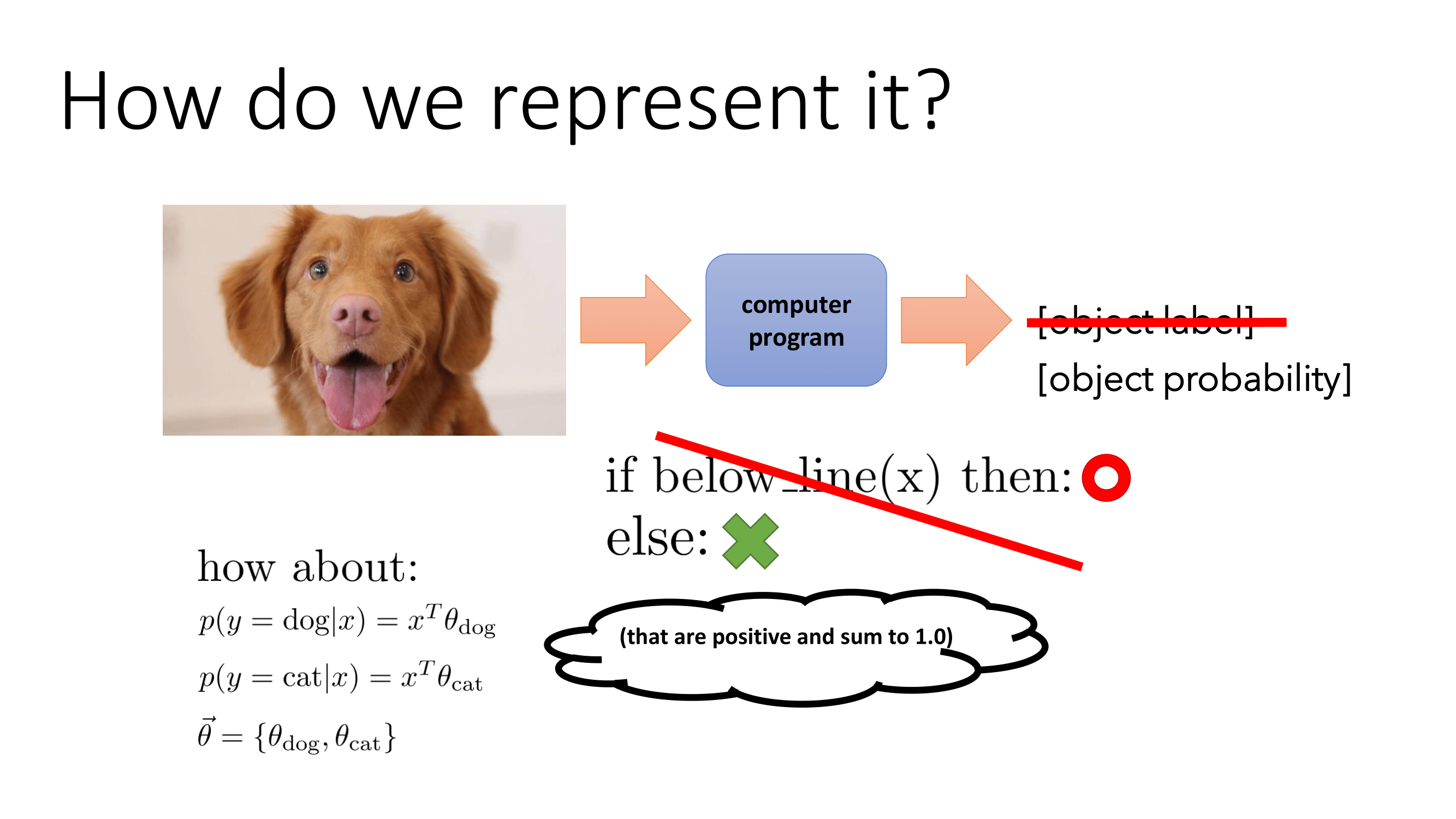
이렇게 되면 우리는 확률값을 구하는 함수가 필요하다. 이 함수는 항상 양수여야 하며 총합이 1이어야 하는 함수여야 한다. 이를 도출하기 위해서는 항상 양이 되는 함수를 먼저 생각해보자. 가장 대표적인 함수는 바로 지수함수이다. 지수함수는 $x$가 $(-\infty,\infty)$에서 $y$는 항상 양수이다. 모든 합이 1이 되게 만드는 방식은 확률을 이용해서 $\frac{z_1}{\sum_{i=1}^nz_i}$로 만들 수 있다. 이를 합치면 다음과 같은 식이 완성된다.

$p(y|x)=softmax(f_{dog}(x),f_{cat}(x))=\frac{exp(f_{dog}(x))}{exp(f_{dog}(x))+exp(f_{cat}(x))}$

이 함수를 1차원으로 표현하면 다음과 같다.

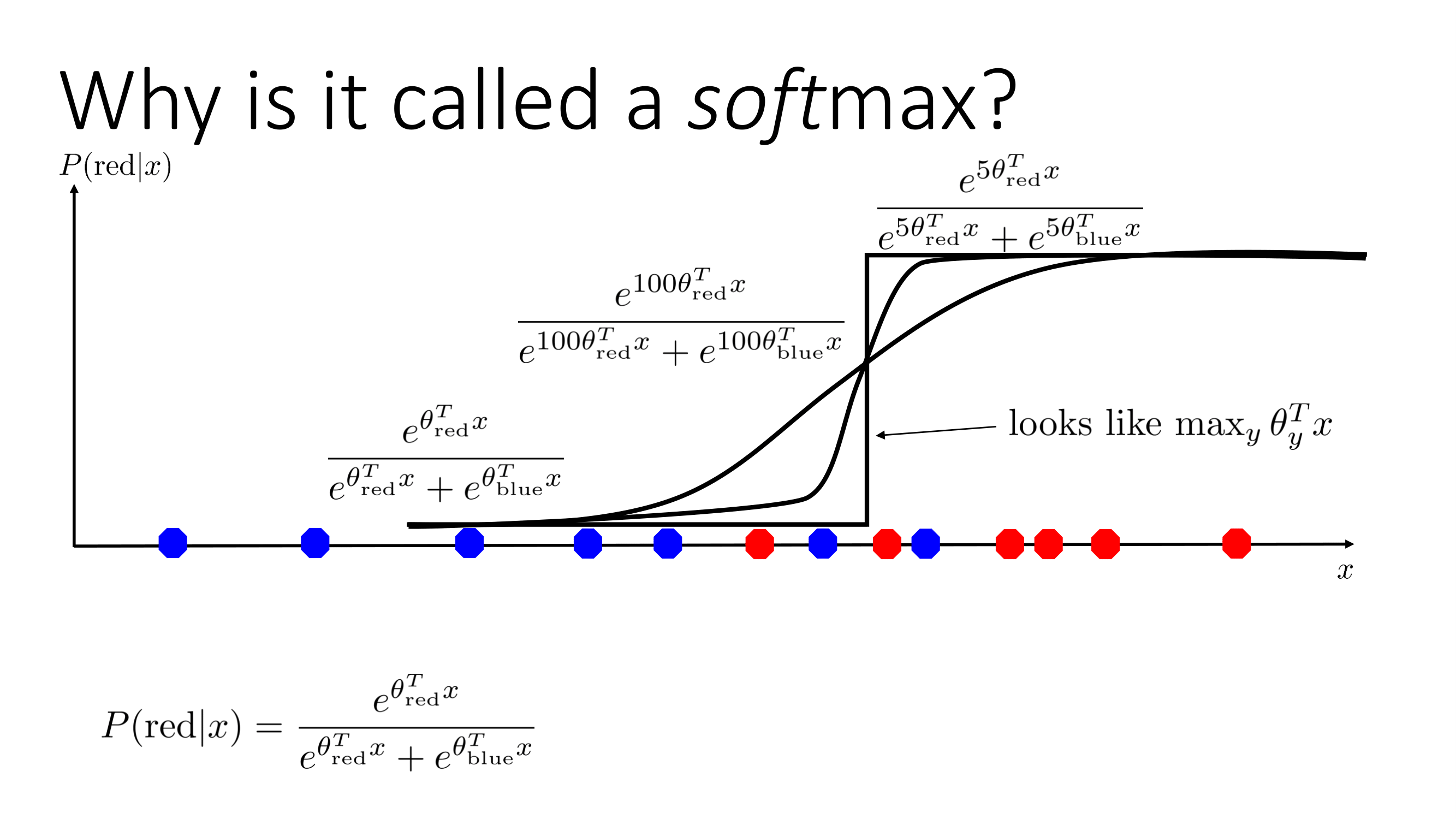
이 함수가 softmax인 이유는 함수에 조금이라도 커지게 되면 0.5부근에서 가파르게 상승한다. 즉 softmax라는 뜻은 말그대로 부드럽게 최대값으로 간다는 뜻이다.

2.2 손실함수 (Loss Function)

손실함수에 대해 알기 전에 우리는 데이터셋이 어떻게 만들어지는지에 대해 알아야 한다. 강아지/고양이 분류기를 예시로 들자. 일단 사진사가 강아지 사진 데이터셋을 만든다. 이떄 사진에 대한 확률분포가 생긴다. 강아지/고양이 사진을 다 찍었을 경우 '강아지'에 대한 label은 label에 따른 조건부 확률분포로 나타날 수 있기에 $(x,y)\sim p(x,y)$로 볼 수 있다.

이때 데이터셋에는 independent and identically distributed(i.i.d.)라는 가정이 붙어야 한다. i.i.d.란 데이터들은 각 데이터에 대해서 독립적이며 고르게 분포되어 있다고 가정하는 것이다. 이 가정이 생겨야먄 $p(D)=\Pi_ip(x_i,y_i)=\Pi_ip(x_i)p(y_i|x_i)$가 성립한다. 우리는 $p_\theta(y|x)$를 학습시킬 것이기 때문에 우리의 목적은 $P(D)=\Pi_ip(x_i)p_\theta(y_i|x_i)$를 최대화시키는 것이라 말 할 수 있다.

해당 식을 로그변환을 해주면 우리의 목적은 $\sum_i\log{p_\theta}(y_i|x_i)$를 최대화시켜주는 것이다. 이때 우리는 해당 식에 마이너스를 붙여 최대화를 최소화로 바꿔주면 우리가 구하려고 하는 손실 함수에 가까워진다.

우리가 구하려고 하는 loss function의 정의는 얼마나 $\theta$가 나쁜지를 측정하는 것이며 우리는 가장 덜 나쁜 $\theta$를 구하려고 하는 것이다. 우리가 아까 구한 negative log-likelihood는 cross-entropy라고 불린다. 또 다른 예로 우리가 처음 가정했던 (확률값이 output이 아닌 바로 결과 나오는 것)에 대한 loss는 zero-one loss이다. 그리고 Mean Squared error 또한 loss function이라 볼 수 있다.

2.3 최적화(Optimization)

2.3.1 Gradient Descent

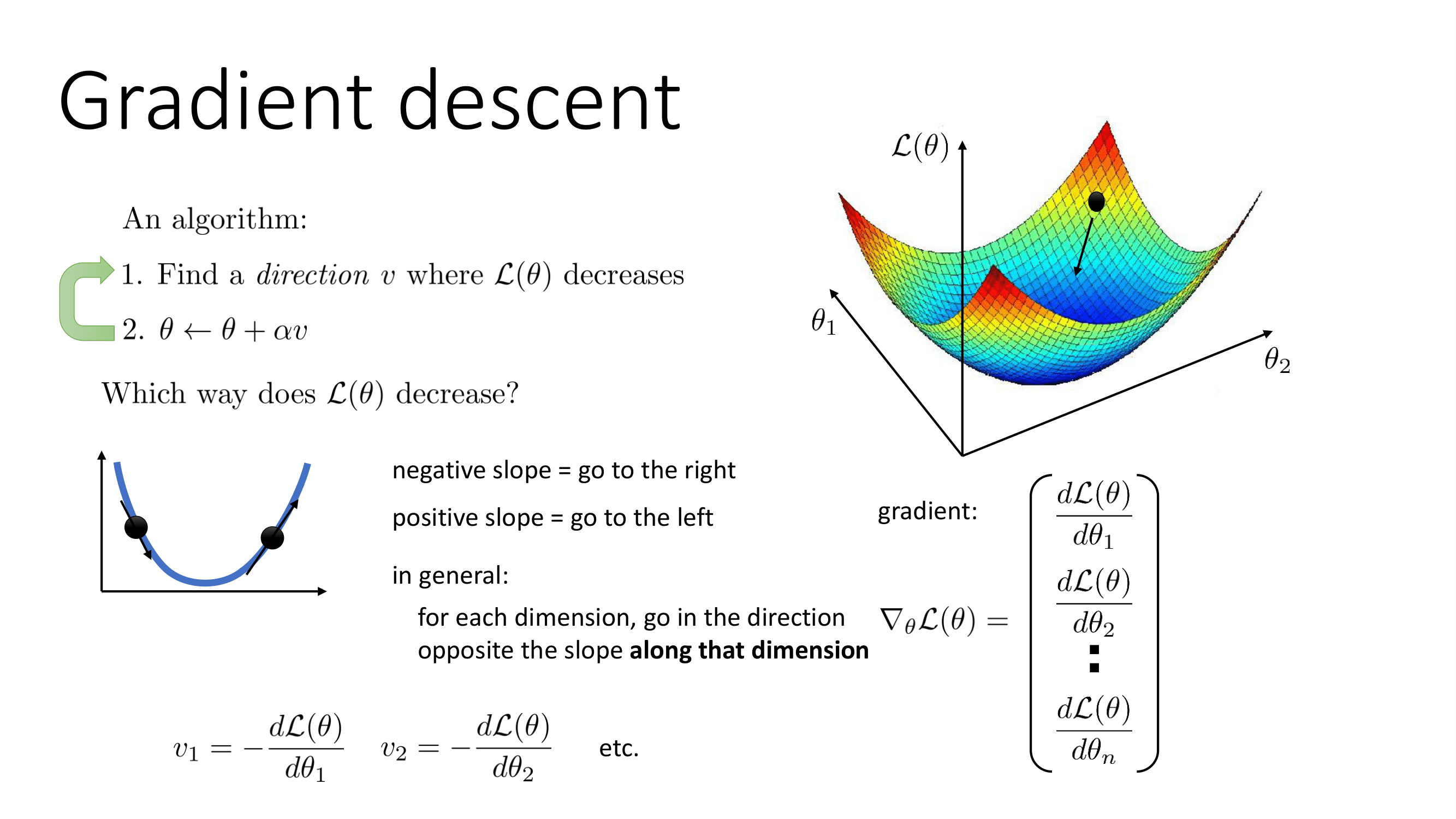
최적화란 우리가 도출했던 손실함수를 어떻게 하면 가장 덜 나쁘게 만드는 방식을 의미한다. 우리가 사용할 방식은 Gradient Descent이다. Gradient Descent의 알고리즘은 다음과 같다.

1. $\mathcal{L}(\theta)$가 작게 만드는 $v$방향을 찾는다.
2. $\theta\leftarrow\theta+\alpha v$

이 방식을 정교하게 만든다면 Gradient Descent는 각 차원에서 해당 차원을 따라 기울기에 반대 방향으로 간다고 정의내릴 수 있다.

2.3.3 예시(Logistic Regression)

2강에서 배웠던 내용을 Logistic Regression을 예시로 설명하면 다음과 같이 만들 수 있다.

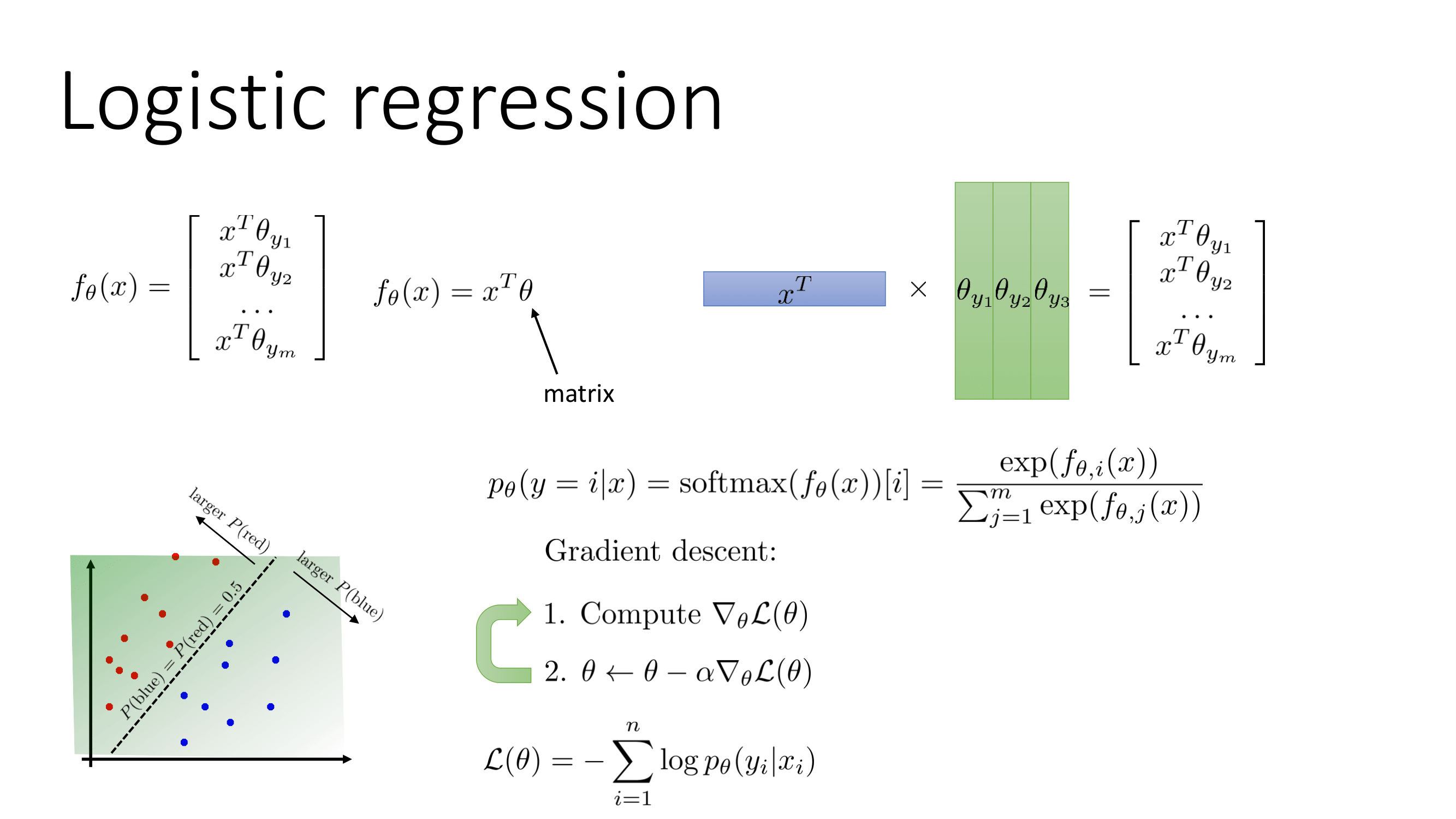
Logistic Regression에서 Binary Classification일 경우 $P(y_1|x)+P(y_2|x)=1$이기 때문에
$P(y_1|x)=\frac{1}{1+e^{-\theta^Tx}}$라고 쓸 수 있고 이를 시그모이드 함수라 부른다.

2.3.4 경험적 리스크와 실제 리스크 (Empirical Risk and True Risk)

Risk란 우리가 잘못될 수 있는 확률을 의미한다. 예를 들어 어떤 행위를 했을때 30%의 확률로 문제가 발생한다라고 했을떄의 30%는 리스크라 볼 수 있다.

Risk에는 Empirical Risk와 True Risk가 있는데
Empirical Risk은 $\frac{1}{n}\sum_{i=1}^{n}\mathcal{L}(x_i, y_i, \theta) \approx E_{x\sim p(x),y\sim p(y|x)}[\mathcal{L}(x,y,\theta)]$로 정의할 수 있다.
이 정의에 의하면 loss function의 평균을 Empirical risk라 볼 수 있다.

보통 지도학습은 Empirical risk를 최소화시키는데 방점이 찍혀 있다. 근데 True risk를 최소화시키는 것과는 다르다. Empirical risk가 낮은데 True risk가 높은 경우를 Overfitting이라 부르며 Empirical risk와 True risk가 모두 높은 경우를 우리는 Underfitting이라 부른다.

정리

2강의 내용은 머신러닝에서 기초에 해당하는 내용이다. 그렇지만 cs182는 타 강의와 다르게 수식적으로 풀어나가고 있어 좀 더 정밀하며 이해도를 높일 수 있었다. 이번 강의에서 제일 놀라운 점은 지도학습이 어찌보면 강화학습의 범주에 속한다라는 이야기였는데.... 해당 교수님이 강화학습쪽으로 유명하신 분이셔서 그런 이야기를 하신것 같다는 생각이 들었다.