본 포스트팅은 인하대학교 컴퓨터공학과 시스템 프로그래밍 수업자료에 기반하고 있습니다. 개인적인 학습을 위한 정리여서 설명이 다소 미흡할 수 있으니, 간단히 참고하실 분들만 포스팅을 참고해주세요 😎
2진수에서 실수 표현하기
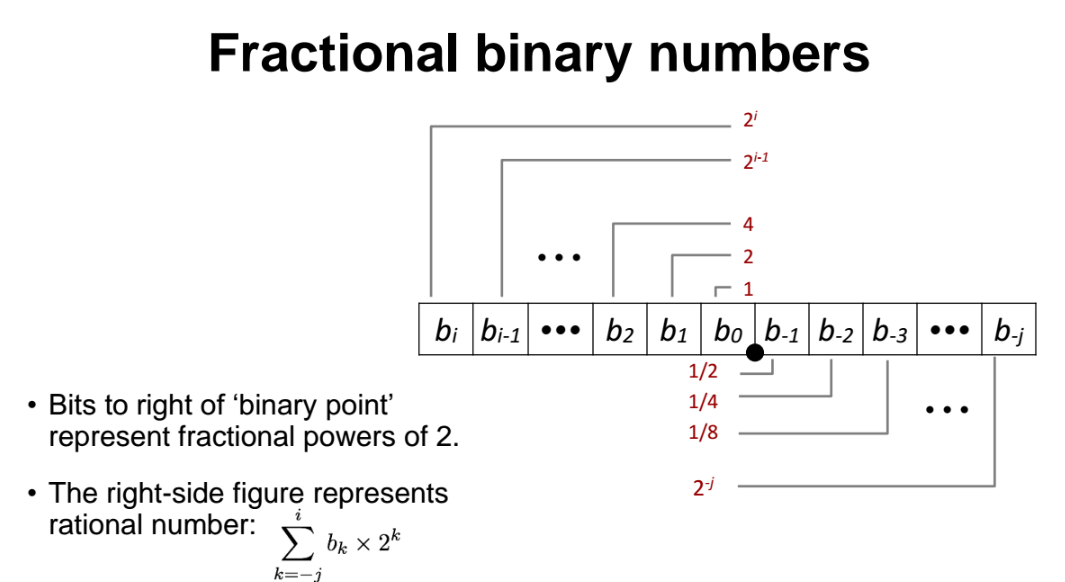
위처럼 . 을 기준으로 표현.
ex) 1011.101 => 소수점 아래부분은 2^-1 + 2^-3 이 된다.
- right shift(우측 연산 쉬프트) : 2로 나누는것과 동일
- left shift(좌측 연산 쉬프트) : 2를 곱하는 것과 동일
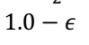
- 위처럼 1에 근사한다는 숫자의 표현을 "1-엡실론" 으로 표현한다.
- 파이(3.141592...) 의 근삿값(숫자)의 표현은 "파이-엡실론" 으로 표현한다.
IEE Floating Point
- floating point number (부동 소수점) 를 표현하는 표준
Floating Point 표현

기호 3개
-
s : sign bit => 부호 비트. s=0 이면 양수, s=1이면 음수
-
M : Significand : [1~2) 사이 범위 (1보다 크거나 같고, 2보다 작은 범위) 에 있는 수 (즉, 1.xxxxx 곱하기 2^E 와 같은 형태로 표현하고 싶은 것이다. 왜 2는 안넘어가나면, 2가 넘는 경우는 E의 값을 조정하여 2를 곱해주면 되기 떄문)
-
E : Exponent => 2의 몇승인지
=> 이 3가지 구성성분이 있다면 모든 소수점에 근사할 수 있다.
Encoding 하기
- 3개의 기호 s, E, M 의 값을 64bit 안에 저장해야하는데, 그냥 저장하면 비효율적이라 인코딩을 해서 저장한다. (값을 인코딩해서 저장한 형태가 효율적이다.)

Encoding 을 한 경우를 생각해보자.
- Floating Point Number 에서 무조건 첫번째 bit 는 s (부호비트)이다.
- Exp 필드는 E (Exponent) 를 인코딩한 결과이지만, 그 결과가 E와 다르다.
- Frac 필드도 마찬가지로 인코딩 결과가 M 과 다르다.
아래 그림은 각 시스템 bit 체계(32 bit, 64 bit, 80 bit 시스템) 에 따라 s, M, E 를 인코딩해서 저장할때 각각 얼마만큼의 공간을 차지하는지 나타낸 것이다.

Normalized Values

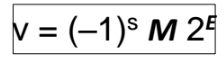
-
Normalized Values 란 앞서 살펴본 공식과 같이 1.xxxx... 에다 2^E 를 곱해준것이다.
-
E 를 인코딩하는 방법 : E = EXP - Bias
-
E는 Bitwise 에 쓸 EXP 에다 Bias 라는것을 빼면 계산된다.
-
Bias = 2^(k-1) -1 => Exp 에 몇 bit를 쓰는가에 따라 결정되는 숫자이다. 예를들어 32비트면 Exp 는 8바이트이므로, 2^(8-1) -1 = 128 - 1= 127이 된다.
-
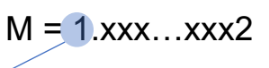
- frac 필드은 xxx...xxx 부분이다.
- frac 필드는 전부 0이면 M=1.0 인 것이고, 반대로 전부 1로 구성되어 있다면 M=2.0-엡실론 (2의 근사값) 이 된다.
아래 예시를 보고 더 이해해보자!
=> Normalized value 로 만드는 과정 : 어떤 숫자가 오던지간에, M이 1로 시작하도록 해당 숫자의 소수점을 맞춰주고, 원래 숫자에 가장 가까울 수 있도록 E 의 값을 결정해서 할당해준다.

1) 위처럼 F = 15213.0 이라는 숫자가 있을 떄 M=1 로 시작하도록 소수점을 맞춰준다. 즉 15213.0 을 2진수로 변환하면 1110...1101 가 되고, 이런 2진수에 대해 소수점을 맞춰주면 1.11011...101 x 2^13 이 된다.
2) 앞서 나온 값 1.110011..1101 x 2^13 에서 1.110011..1101 값이 M 이 되고, 13 이 E가 된다.
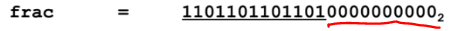
3) 이에 따라 frac 은 M의 소수점부분 값인 11011..101 이 된다. 그런데 32bit 시스템이므로(float형은 single precision으로, 32bit 시스템을 가지기때문) frac 이 23bit 의 공간을 차지하므로 11011..101 값으로 채워도 빈 공간이 생기는데, 이 빈공간은 모두 0 으로 채워준다.
4) Bias 값을 계산해보자. 2^(8-1) - 1 = 127이 된다.
5) Exp = E + Bias 이므로, Exp = 13 + 127 = 140 이 된다. 그리고 2진수로 변환하면 10001100 이 된다.
6) 추가적으로 원본 숫자가 양수였으므로, sign bit 은 당연히 0이다.
7) 최종적으로 아래와 같은 결과를 얻을 수 있다.

Denormalized values

숫자가 너무 작으면 M 부분이 1로 시작하지 못하고 0.xxxx 형태의 숫자로(즉 0초과 1이하 범위 사이의 숫자) 시작해야 할수도 있다.
=> E 가 쓸수있는 정해진 범위가 있기떄문이다. 표현 가능한 숫자의 범위는 0~255 사이, -128 ~ 127 사이로 범위가 있다. 즉, 2^E 를 통해 -128 밑의 범위는 표현이 불가능하다. 그래서 E의 값으로 가능한 가장 작은 값인 E=0 값보다 더 작아지면 M=1 로 둘 수 없을만큼 작아서 M = 0.xxxx.... 과 같은 형태가 나올 수 있다.
=> 이런 경우를 Denormalized values 라고 한다. 왜냐하면 M=1.xxx 과 같은 형태가 안되기 때문.
2가지 case
- exp = 0, frac = 0 이면 M=0이다.
- exp = 0, frac != 0 이면 M=0.xxxx 이다.
Tiny Floating Point 예시
시험출제!!! 꼼꼼히 공부하자!
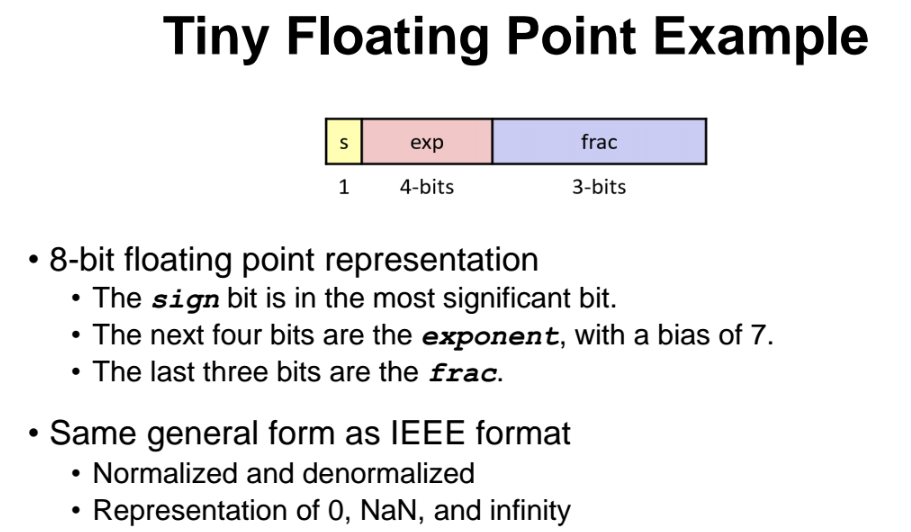
8bit짜리 시스템의 floating point 표현방법을 살펴보자.
-
sign bit 을 1bit 쓰고, exp 를 4bit 쓰고, frac 을 3bit 쓴다.
-
bias = 2^(4-1) - 1 = 7이다. 즉 2의 지수를 저장할때 7을 빼서 저장한다.
-
frac은 3bit 이므로 1.xxx 에서 뒤의 소수점 3개를 저장한다.
예시
아래 표를 참고해서 몇가지 case에 대해 8bit 자리 floating point 임을 가정하고
값(value) 를 계산해보자.
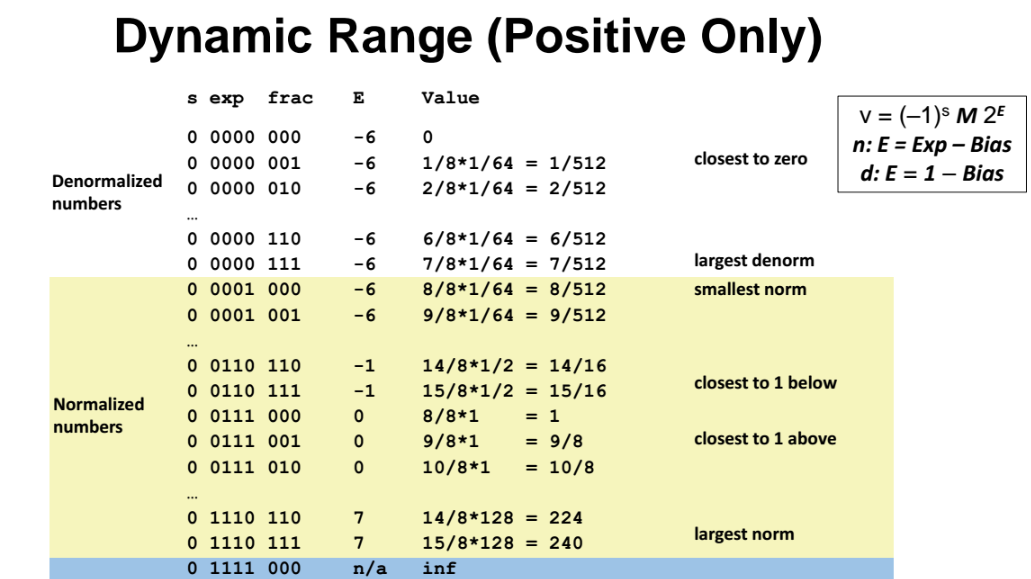
우선 아래의 case 에 대해 계산해보자.

- 우선 exponent(exp) 의 값은 0이다. 그리고 앞서 계산했듯이 bias = 7 인데 denormalized values 이므로 (exp = 0, E = 1 - bias = 1-7 = -6 이다.
E = -6 이므로 즉 2^E = 2^-6 = 1/64 이다.
아래 공식을 통해 value 를 계산해보면 M = 1/8 (frac 이 001 이므로) 이고, 2^E = 1/64 이고, s = 0 으로 주어졌으므로
=> value = 1 x 1/8 x 1/64 = 1/512 이 된다.
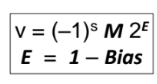
하나만 더 연습삼아 해보자.
s=0, exp=0110, frac=110 인 경우이다.

-
bias의 값은 그대로 bias = 7 이고, normalized numbers 임을 가정했으므로
E = exp = bias = 6 - 7 = -1 이다. -
그리고 frac = 110 이고, normalized numbers 임을 가정했으므로
M = 1.110 = 3/4 + 4/4 = 7/4 = 14/8 이 된다.
=> 따라서 value = (-1)^s x M x 2^E = 1 x 14/8 x 1/2 = 14/16 이 된다.
Distribution of Values
이이서 6bit 짜리 시스템에서 floating point 표현했을때에 대해 알아보자.
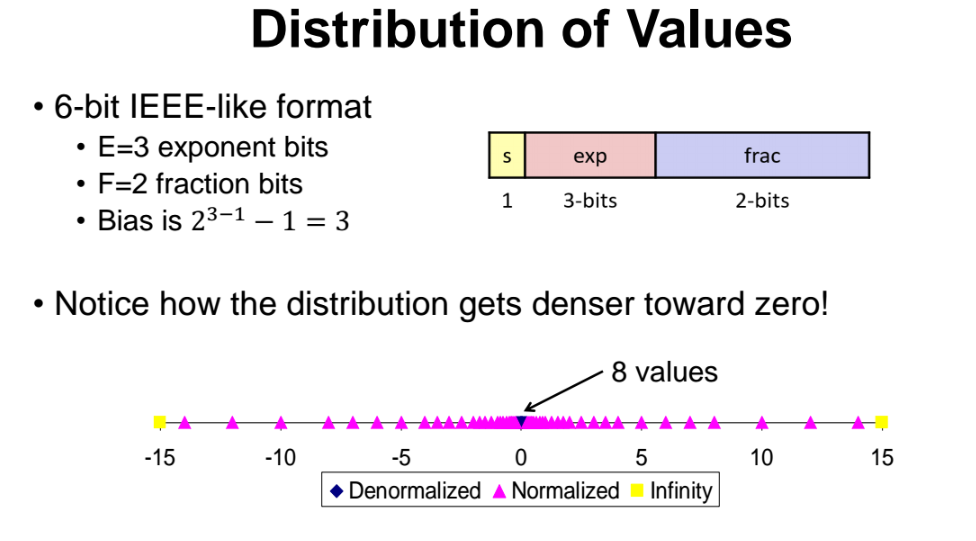
-
exp 가 3bit 이고, frac이 2bit 이다.
-
이에따라 bias = 2^(3-1) - 1 = 3이된다.
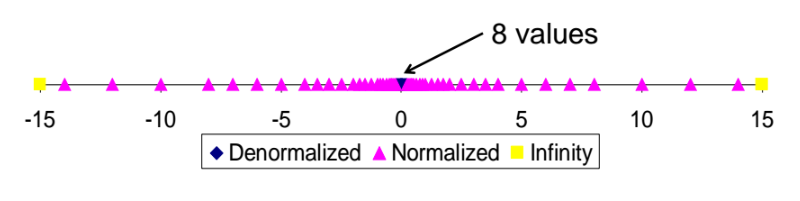
실제로 value 값들을 찍어보면 위와 같은 그래프가 나온다.
-15 ~ 15 사이의 범위에 분포해있으며, 0 근처로 갈수록 촘촘해지고 벗어날수록 띄엄띄엄 분포해있다.
=> 이렇듯 6bit 짜리 시스템에서 floating pointer number 로 표현가능한 숫자들은, 0근처의 값들은 촘촘하게 대부분 값들을 표현 가능하나 0에서 벗어날수록 표현 불가능한 숫자들이 많아진다.
floating point number 는
- 1) bit 가 많은 시스템일수록 큰 숫자들에 대해 더 정확하고, 표현 가능한 숫자들이 많아진다. 반면 작은 숫자들에 대해선 부정확하고, 표현 가능한 숫자들이 적어진다.
- 2) 반대로 bit 가 적은 시스템일수록 큰 숫자들에 대해 더 부정확하고, 표현 가능한 숫자들이 적어진다. 반면 작은 숫자들에 대해선 정확하고, 표현 가능한 숫자들이 많아진다.
( 그래서 위에서 보는 6 bit 짜리 시스템에서는 작은 숫자들에 대해서 표현 가능한 것들이 많은 것이다. )
앞선 6 bit 시스템에서 -1~1 사이의 범위를 더 확대해서 자세하게 살펴보자.
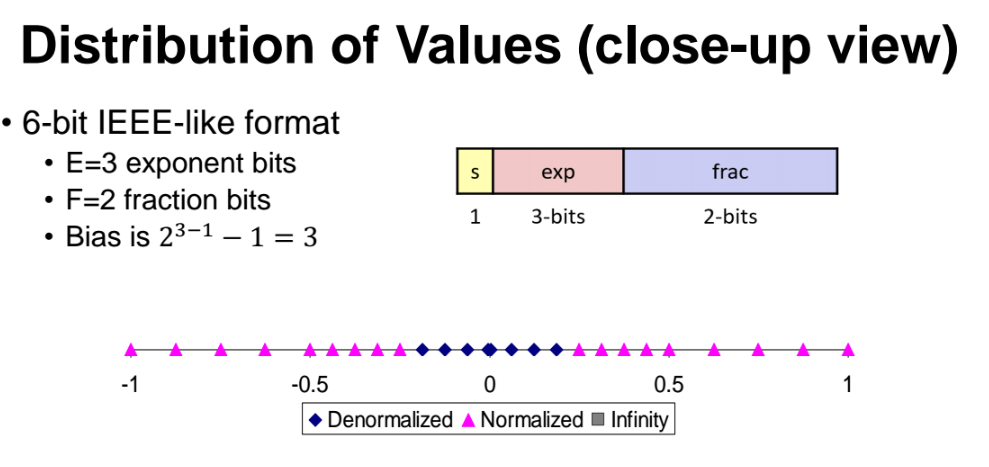
- 핑크색 점을 보면 알듯이 normalized value 를 표현 가능한 범위는 -1~1 사이의 숫자이다. 그런데 0에 거의 근접할 만큼 엄청 작은 숫자에 대해서는 표현 불가능한 숫자이다. 즉 0에 거의 근접한 숫자에 대해서는 denormalized value 로써 표현 가능하다.
Floating Point Operations
- Floating Point (소수점 숫자) 에 대해서 사칙연산을 했을때 어떤 변화가 나타나는지를 살펴보자.
floating point number 들은 "근사한" 값들 이므로, 해당 bit 시스템에 맞춰서 가능한 값으로 최대한 Rounding 을 해줘야한다.
- Rounding 이란? : 소수점 . 을 올리거나 내리는 것
=> 소수점을 어떻게 올리고 내리는지 방법이 표준적으로 정의가 되어있다.

두 피연산자 x 와 y 를 더하거나 곱할때, x와 y가 정수라면 그냥 단순히 더하고 곱해주면 된다.
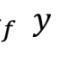
=> f 를 붙여주는 것은 값 y가 타입이 float 이라고 표시한 것이다.
이렇게하면 앞서 배운 floating point number 의 특성때문에, 우리가 생각해 볼 수 있는 x 와 y에 대한 더하기(곱하기) 연산의 결과값과 다르다.
=> 그래서 항상 계산을 실제로 앞서 실제값에 대해 게산을 한 다음에, 계산된 결과에다 시스템의 bit 에 따라서 Round를 적용해줘야한다.
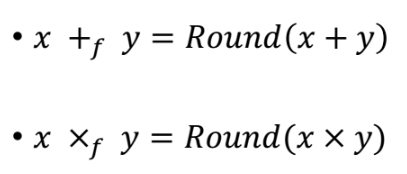
그림을 다시보자. 실제로 x, y의 정확한 값(우리는 계산을 못하는 이상적인 정확한 값) 에 대해서 x+y 연산을 진행하고 그 결과값x+y 에 대해 Rounding 한 결과( = Round(x+y)) 가 나온다.
예시
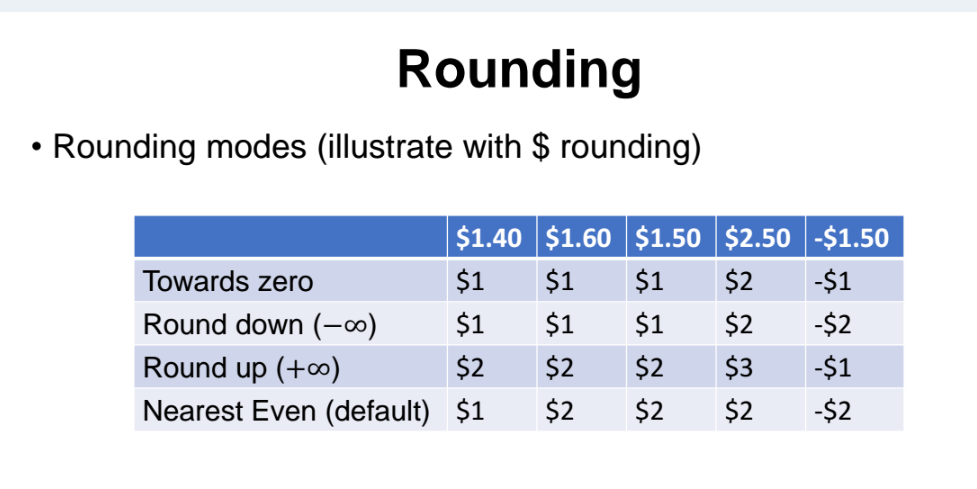
4가지 rounding mode 가 있다.
- towards zero 라는 rounding 을 하면 0에 가까운 값으로 수렵한다.
이 외에도 round down, round up, nearest even 라는 모드가 있다.
우리는 Nearset even 이라는 rounding mode 를 가장 많이 사용한다.
- nearest even : 이진수로 바꿨을때 우리가 저장할 수 있는 bit의 가장 마지막 숫자 LSB 가 짝수여야한다. LSB 가 짝수면 올림되고, 홀수면 버려진다.
Rounding Binary Numbers
- Binary Fractional Numbers :
- 1) 이진수 숫자로 바꿔놨을 떄 LSB 가 0이면 짝수이다.
- 2) 반올림의 기준값(중간점)은 100...(2)이다.
- CASE1) 중간값을 기준으로 더 작다면 버리고, 더 크다면 올림한다.
- CASE2) 정확히 중간점에 있을때, LSB를 확인해서 기존 숫자가 짝수인지 홀수인지 판단한다. 만일 기존 숫자가 짝수라면, 그리고 올림했을 때와 버림했을 때 결과가 짝수인 경우를 선택해줘서 올림 or 버림해주면 된다.
( => ex. 기존 숫자가 짝수이고 올림 했을때가 짝수, 버렸을때가 홀수라면 올리을 해주는 것이다. )
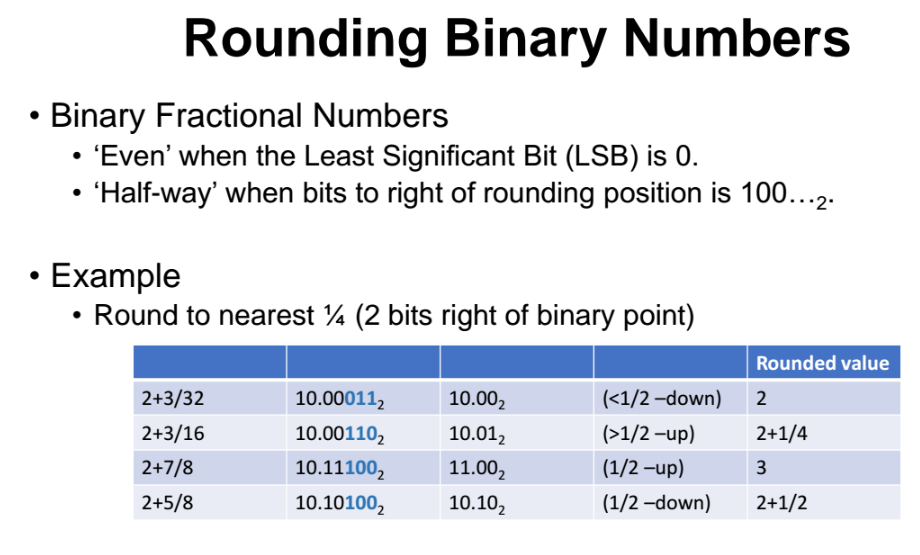
예제
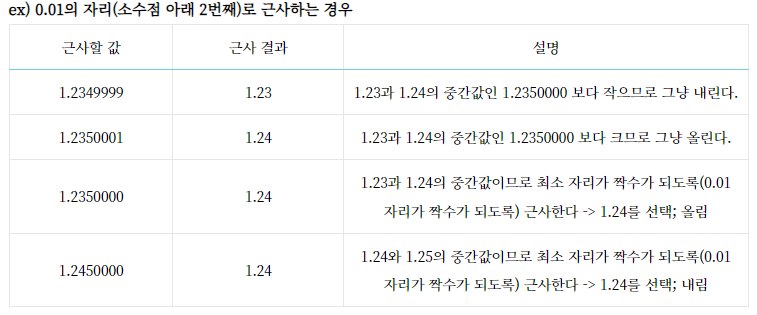
우리가 소수점 기준으로 2개의 bit 까지만 저장할 수 있다고하자. 그러면 소수점 3번쨰 bit 부터는 round 를 해줘야한다. 즉, 3번쨰 이하의 bit 숫자들에 대을 소수점 2째자리 bit 숫자로 올림을 해줄지 아니면 버릴지를 해줘야한다.
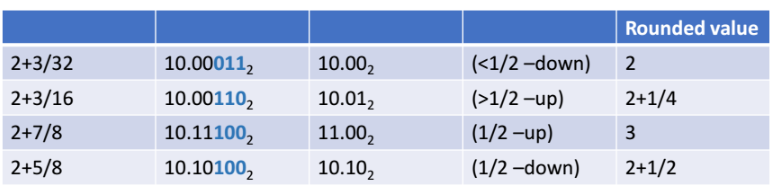
- 2+3/32 : 원래 값
- 10.00011 : 2진수로 변환한 값
- 10.00 : round한 결과
- 2 : rounded value (round한 결과를 10진수로 바꾼 값)
1) 10.00011 에서 011은 중간값(반올림 기준값) 100 보다 작아서 버려진다. 그 결과 10.00이 된다.
2) 10.00110 에서 110은 보다 더 커서 올림해준다. 그 결과 10.01이 된다.
3) 10.11100 에서 100은 정확히 1/2 이다. 올림하냐 버리냐를 판단하기 전에 LSB를 먼저 살펴보면 0이므로 이 숫자는 짝수이다.
-
올림을 안하고 버린다면 => 결과값이 10.11로, LSB를 확인해보면 홀수가 된다. 따라서 짝수가 홀수로 변하는 것은 안되므로 올림을 해줘야한다.
-
올림을 진행하면 => 결과값이 11.00 으로 LSB 를 확인해보면 0이므로 짝수가 올림을 진행하면 그대로 짝수가 나오는 것이다. 따라서 올림을 진행해주면 된다.
4) 10.10100 에서 100은 정확히 1/2 이다. 올림 여부를 판단전에 LSB를 확인해보면 0이므로 해당 숫자는 짝수이다. 이 경우는 올림을 하면 LSB가 1이 되버려서, 짝수가 아니게 된다. 따라서 올림하지 않고 그냥 버려줌으로써 짝수가 되게한다. 결과값은 10.10 이다.
반올림(rounding) 의 중간점에 걸치는 경우는, 만일 변환했을 떄 LSB 값에 따라서 짝수가 되는가 아닌가에 따라서 올림 해주냐 마냐가 결정된다.
Floating Point 곱셈
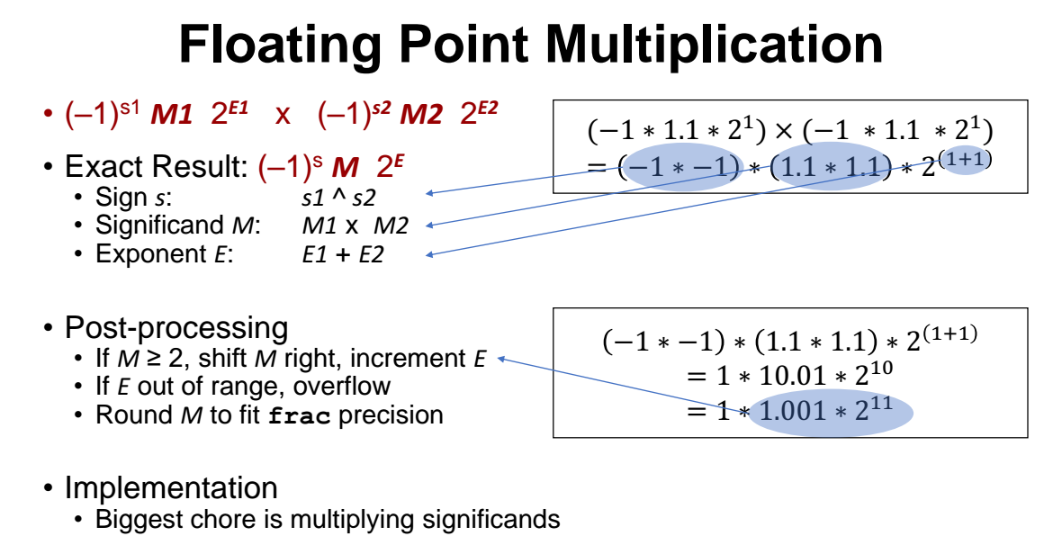

위와 같은 형태릐 Floating Pointer 숫자 2개를 곱한다.
곱한 결과 sign bit, M, E 의 상태는 아래와 같을것이다.

- Sign S : s1와 s2가 다르면 음수를 표현하기 위해 1이 되고, 같으면 양수를 표현하기 위해 0이 될 것이다.
- M = M1 X M2
- E = E1 + E2
Post-Processing
=> 이렇게 계산하면 M 에 대해 문제점이 발생할 수 있다. M1 X M2 결과가 1~2 사이의 값이여야 하는데, 이 범위를 넘어선 결과값일 수 있다.
E 도 문제가 발생할 수 있다. 2^E1 X 2^E2 = 2^(E1+E2) 결과가 나올텐데, 이 값이 너무커서 표현 가능한 범위를 넘어설 수도 있다.
따라서 이렇게 오버플로우가 발생할 수 있으므로 반드시 shift 연산을 해줘야한다. 이럴 때 좌측or우측 쉬프트를 진행해주는 것을 Post-processing 이라고한다.
아래 예제처럼 M=10.01 인데 1~2 사이의 값이 아니다. 따라서 shift 을 해줘서 10.01 을 1.01 로 만든다. (M=1.xxxxx 형태가 되었다!)
그러고 지수 값에 1을 더해준다. 그러면 2^10 이 2^11 가 되었다.
Floating Point 덧셈
덧셈은 어떻게할까?
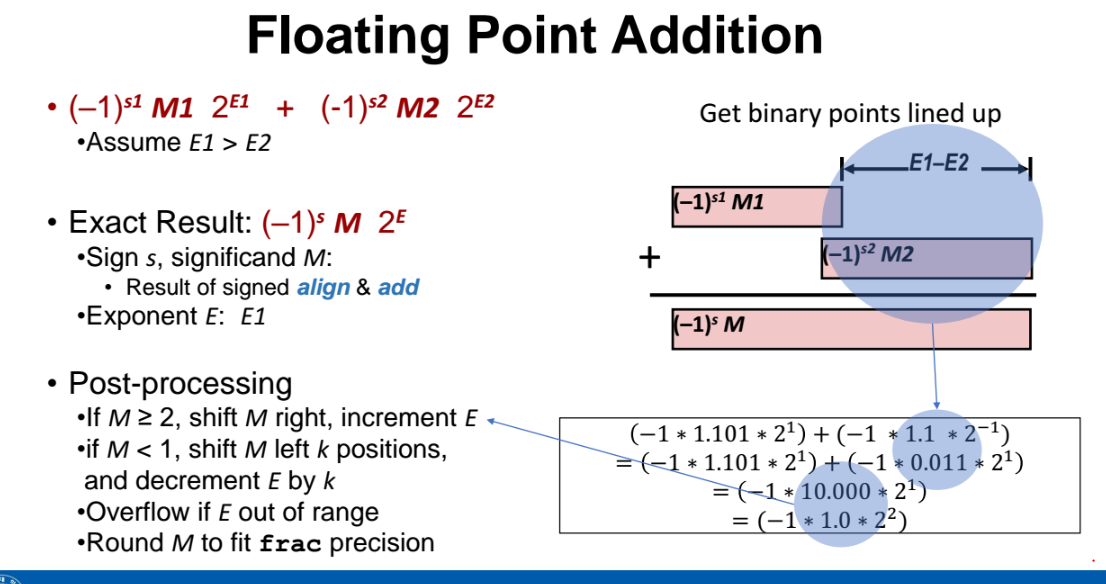
sign 관련
- 부호를 확인하고 새롭게 계산해야한다.
M 관련
-
M1 과 M2 의 자릿수가 다르다면 그냥 바로 더하지 못한다.
-
M은 어떤것은 Normalized, 또 어떤것은 DeNormalized 가 될 수 있다. 그래서 간단하게 M1, M2 를 바로 더하는것이 아니다.
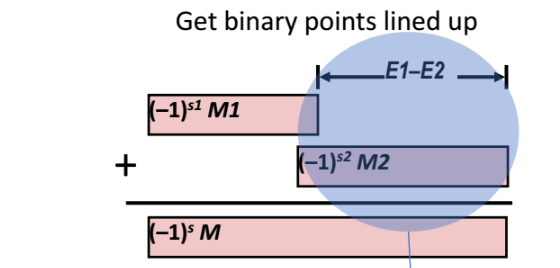
- M1 이 M2보다 더 크다고 가정해보자. 그러면 큰 값인 M1 을 오른쪽으로 밀고, 작은 값 M2 를 왼쪽으로 밀어낸다. 지수값 E1 에서 E2 만큼을 뺀 값(E1 - E2) 만큼을 밀어내면 된다. 그리고 더하면 된다.
=> 쉽게말해, 두 피연산자자의 지수 승 E를 똑같이 맞춰주고 연산해주면 된다.
=> 더한결과 M 값이 도출되고, 이 M 값은 지수값이 E1이 될것이다.
예를들어 두 Floating Point Number 가 둘다 1.1 이라고 하고 덧셈을 한다고 해보자. 그런데, 이 둘을 더한 결과가 2.2가 되지 않는다.
=> 왜냐하면 지수의 승에 따라서 각 피연산자는 예를들어 1.1x2^1, 1.1x2^-1 일수도 있다.
그러면 M1, M2 값은 모두 1.1인데 뒤에 붙은 지수 승 때문에 한 놈이 커지고, 다른 한놈이 작아진다. 따라서 M1 과 M2 를 직접 더하려면 M1 과 M2 사이에서 큰 지수승을 가진 녀석에게 맞춰주는 것이다.
아래 예제를 보자. 둘은 지수승이 2^1, 2^-1 으로 다르다. 2번째 피연산자를 E1-E2 만큼 밀어줘서 M1 과 M2를 계산하기 적절하게 자릿수를 조절해주면 바로 계산이된다.

앞선 과정으로 M1 과 M2 에 대해 바로 계산이 되도록 셋팅되었다면,
곱셈 연산과 동일하게 Post-processing 을 진행해준다.
- 곱셈과 동일하게, M 값(=M1xM2) 가 2보다 커지거나 1보다 작아져서 오버플로우가 발생한 경우 Rounding 을 해준다.

실제 값을 Floating Point 에 저장하기
실제 값을 Floating Point 에 저장해서 Floating point 숫자로 만드는 방법을 알아보자. 아래 예시에서는 실제 값을 소수가 아닌 정수값에 대해 Floating point 를 적용해보는 것을 살펴보겠다.

과정
1) 실제값 정수를 2진수로 변환한다. (컴퓨터는 2진수밖에 해석 못하니깐)
2) M=1.xxx 가 될수있도록 자릿수를 맞춰준다. 그러면서 자연스래 frac 와 E 값을 생성한다.

즉 아래처럼, M 값을 변형시켜줌에 따른 frac 을 만들고 (이떄 새롭게 채워지는 bit는 전부 0으로 채워줌)
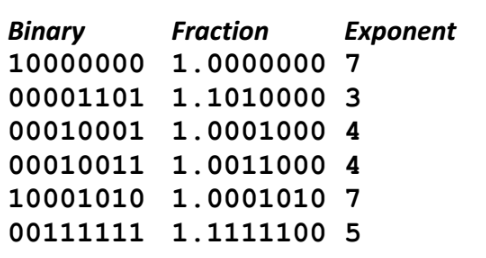
E 값도 생성해준다.

3) Rounding 을 해준다.
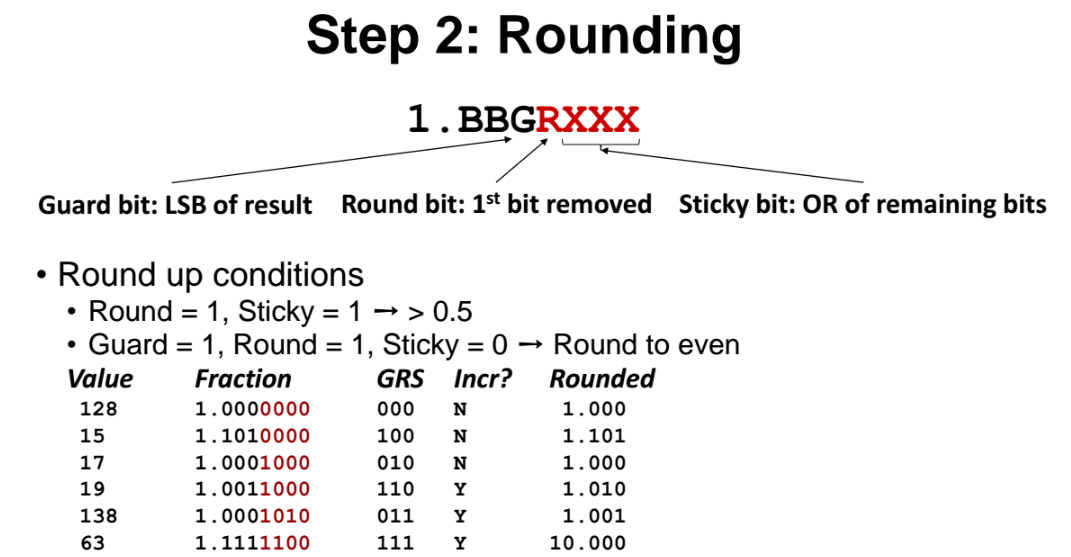
그런데 frac 부분에는 bit 를 3개까지 밖에 저장을 못하므로, rounding 을 해줘야한다. rounding 을 해서 소수점 3째자리에 대해 반올림을 해준다.
- cf) 위 그림에서 Incr 은 올림여부이다. 즉 Incr 이 N이면 올림안하고 버린것이고, Y이면 올림한거다.
4) Post-normalize 를 해준다.
앞선 rounding 을 통해 오버플로우가 발생한 값에 대해 진행해주면된다.

c언어에서의 Floating point 구현
c언어에서 Floating point 가 어떻게 구현되어 있는지를 알아보자.

casting(형변환) 과정을 하는것을 보자.
- double 또는 float 타입 -> int 타입으로 변경하느 경우
- rounding 이 발생하며 소수점이 없어지면서 int 타입으로 바뀐다.
- int 타입 -> double 타입
- frac 의 공간이 넉넉해서 값이 손실되지 않고 정상적으로 변형된다.
- int 타입 -> float 타입
- 값이 손실될수도 있고 정상적으로 손실되지 않고 변형될 수 있다.
c언어에서 다양한 타입간의 형변환

