1. 그래프 표현 방법(코드 중심)

그래프는 인접 행렬(adj matrix) 또는 인접 리스트(adj list)로 표현할 수 있다
인접 행렬로 코드를 작성하는 것을 설명하자면,

먼저 가중치가 없는 간선을 표현하는 클래스를 만든다
이 클래스에서는 1은 노드끼리의 연결을, 0은 연결되지 않음을 의미한다
그리고 위 클래스를 상속받아 가중치가 있는 간선을 표현하는 클래스를 만든다
여기서는 가중치가 없는 간선 클래스와는 다르게 특정값이 표현되면 연결됨을, INF값으로 표현되면 연결되지 않음을 의미한다
INF는 코드 작성하기 전에 위에서 define으로 정의한다

위의 말을 간단하게 표현하면

가중치 X Class{
} #1은 연결, 0은 연결 x
가중치 X Class를 상속받은 가중치 O Class{
} #특정값은 연결, INF값은 연결 x

처럼 표현할 수 있다

이제 수업시간에 배운 코드를 이용하여 설명을 하자면

#include <iostream>
#include <queue>
#include <vector>
#include <set>
#include <map>
#include <limits>
using namespace std;

template <typename T>
struct Edge {
	unsigned src; // 시작 정점
	unsigned dst; // 끝 정점
	T weight; // 가중치
};

template <typename T>
struct Label {
	unsigned ID;
	T distance; //거리
	inline bool operator> (const Label<T>& l) const {
		return this->distance > l.distance; //새로 구한 거리가 기존 거리보다 짧으면 업데이트를 하는데 이를 확인하기 위해 비교
                                           // 연산자 오버로딩(탬플릿이여서 대소비교가 안된다)
	}
};

template <typename T>
class Graph { //나머지도 탬플릿이여서 그래프도 탬플릿 형식으로 만든다
public:
	Graph(unsigned N) : V(N) {}
	auto vertices() const { return V; }
	auto& edges() const { return edge_list; }
	auto edges(unsigned v) const { //내가 원하는 정점 입력하면
		vector<Edge<T>> edges_from_v;
		for (auto& e : edge_list) { //모든 간선(edge_list)들을 보면서 시작점이 원하는 점이면 
			if (e.src == v)
				edges_from_v.emplace_back(e); //그 친구들을 임시로 만든 edges_from_v에 넣어줌
		}
		return edges_from_v; //이어진 간선들의 구조체가 리턴된다
	}
	void add_edge(Edge<T>&& e) { //간선 구조체를 가져와서 매개변수로 바꾸기 때문에 2번 참조 표시함
		if (e.src >= 1 && e.src <= V && e.dst >= 1 && e.dst <= V) //1번 정점부터 8번 정점까지
			edge_list.emplace_back(e); // 전체 그래프의 간선들의 집합에 (내가 넣고 싶은) 새로 넣은 간선을 추가함
		else
			cerr << "errors" << endl;
	}
	template <typename U>
	friend ostream& operator<< (ostream&, const Graph<U>& G); //다른 클래스의 맴버를 사용하기 위해(friend) 사용
private:
	unsigned V; // 몇개의 정점으로 구성되어 있는지
	vector<Edge<T>> edge_list; // 간선들의 집합
};

template<typename U>
ostream& operator<< (ostream& os, const Graph<U>& G) { //다른 클래서에서 가져오는거기 때문에 U라고 새로운 이름으로 지정
	for (unsigned i = 1; i < G.vertices(); ++i) { 
		os << i << ":\t";
		auto edges = G.edges(i); // 8개의 간선 가져오기 auto로 해야지 코드 형태가 바뀌어도 알아서 바꿔줌
		for (auto& e : edges)
			os << "{" << e.dst << ": " << e.weight << "}, ";  
		os << endl;
	}
	return os;
}

template <typename T>
auto create_reference_graph() { //그래프 만들기 객체로 넘기기 때문에 auto사용
	Graph<T> G(9); //정점 9개인 그래프
	map<unsigned, vector<pair<unsigned//(목적지), T>>> edge_map; //t와 t와 연결된 요소들이 pair로 연결
	edge_map[1] = { {2, 2}, {5, 3} };
	edge_map[2] = { {1, 2}, {5, 5}, {4, 1} };
	edge_map[3] = { {4, 2}, {7, 3} };
	edge_map[4] = { {2, 1}, {3, 2}, {5, 2}, {6, 4}, {8, 5} };
	edge_map[5] = { {1, 3}, {2, 5}, {4, 2}, {8, 3} };
	edge_map[6] = { {4, 4}, {7, 4}, {8, 1} };
	edge_map[7] = { {3, 3}, {6, 4} };
	edge_map[8] = { {4, 5}, {5, 3}, {6, 1} };
	for (auto& i : edge_map) 
		for (auto& j : i.second)
			G.add_edge(Edge<T>{i.first, j.first, j.second}); // map들 보면서 edge넣어줌
	return G;
}

int main() {
	using T = unsigned;
	auto G = create_reference_graph<T>();
	cout << "Reference graph" << endl; //내가 만든 그래프 auto형식으로 메인에서 가져올 수 있음
	cout << G << endl;
    
    return 0;
}

2. 다익스트라 알고리즘

다익스트라(Dijkstra)란?

하나의 정점으로부터 모든 다른 정점까지의 최단 경로를 찾는 알고리즘이다

그래프를 G=(V,E)로 표현했을 때 V는 정점, E는 간선을 의미한다
여기서 E에 가중치가 있고 최단거리를 이용할 때 다익스트라를 사용한다
그리고 E에 가중치가 없을 때에는 BFS를 사용한다

다익스트라는 음수인 가중치가 있으면 안된다
다익스트라 알고리즘을 구현하기 위해서는

1.처음 시작할 때에는 시작 정점을 방문하고 그 이후에는
2.방문하지 않은 정점 중 가장 가중치 값이 작은 정점을 방문한다
3.그 후 해당 정점을 거쳐서 갈 수 있는 정점의 거리가 이전에 기록한 값보다 작다면 그 거리를 갱신한다

다음 그림 예시를 보면서 이해를 해보자면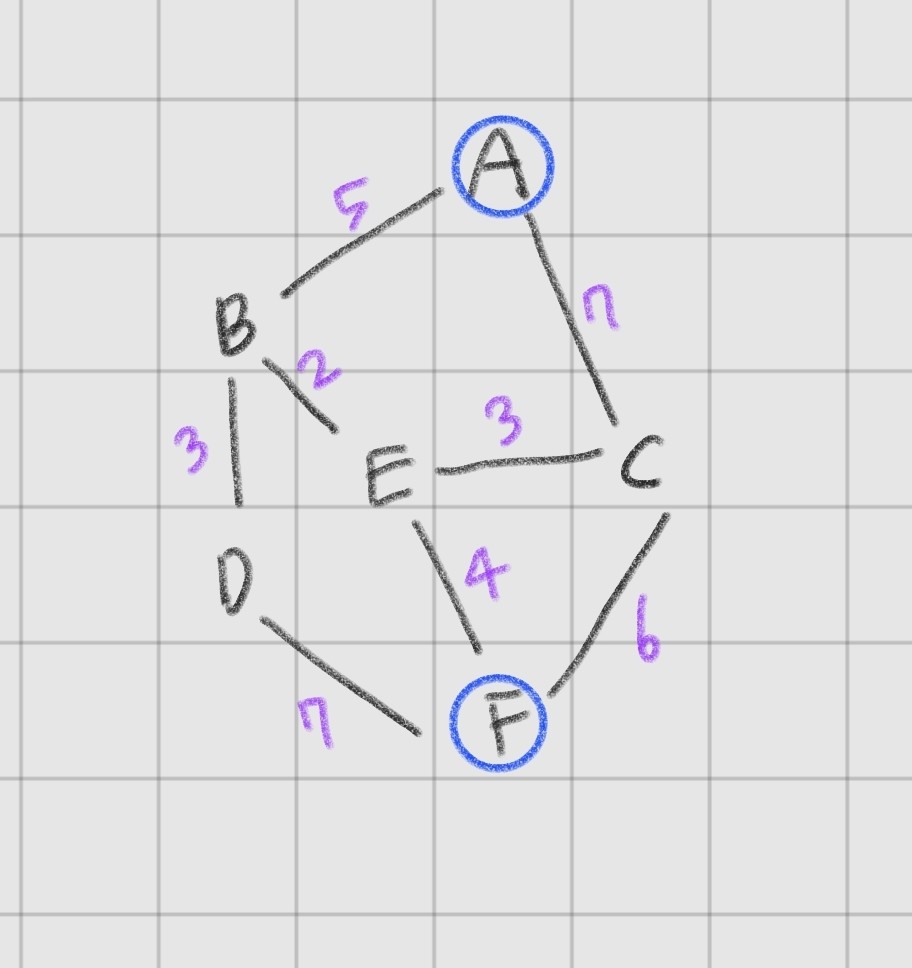보라색 숫자는 각 간선의 가중치를 의미하고 A에서 F까지 가는 최단 경로를 찾아본다
먼저 A가 갈 수 있는 정점은 B와 C이다
B와 C 중에서 가중치가 작은 B로 이동을 하게 된다
그 다음 가중치가 작은 E로 이동을 한다
E에서 아직 방문하지 않은 정점은 C와 F이고 우리는 F로 가야하기 때문에 E와 C가 연결된 간선의 가중치가 작지만 바로 F로 이동을 하면서 알고리즘을 마무리 한다
결론적으로 A에서 F까지 이동하는 최단 거리는 A-B-E-F가 된다

추가로 다익스트라는 O(n^2)의 시간 복잡도를 가지고 있다

코드 구현

위에서 이해한 다익스트라를 코드로 구현해보자면 아래 코드 처럼 표현할 수도 있다
첫번째 코드는 위의 그래프 코드 중 다익스트라 부분을 추가적으로 작성한 것이다

#include <iostream>
#include <queue>
#include <vector>
#include <set>
#include <map>
#include <limits>
using namespace std;

template <typename T> //다익스트라 알고리즘
auto CDIJKSTRA(const Graph<T>& G, unsigned src, unsigned dst) {
	priority_queue<Label<T>, vector<Label<T>>, greater<Label<T>>> heap; //priority 큐 만들고 중간중간 경로 저장함 최소힙으로 만들기 위해 greater사용
	vector<T> distance(G.vertices(), numeric_limits<T>::max()); //거리 정보
	set<unsigned> visited;//방문 여부
	vector<unsigned> parent(G.vertices()); //각각의 점이 이전에 어떤 점을 지나야 최소 경로인지 확인
	heap.emplace(Label<T>{src, 0}); //소스 거리는 0
	parent[src] = src; 
	while (!heap.empty()) { //힙에다가 거리 정보 넣어줌(최소힙) 
		auto current_vertex = heap.top();
		heap.pop();
		if (current_vertex.ID == dst) { //목적지 여부 파악하고 아니면 넘어가기
			cout << "Arrived at the destination vertex " << current_vertex.ID << endl;
			break;
		}
		if (visited.find(current_vertex.ID) == visited.end()) {//set으로 만든 컨테이너 사용
			cout << "Arrived at the vertex " << current_vertex.ID << endl;
			for (auto& e : G.edges(current_vertex.ID)) {
				auto neighbor = e.dst; //간선들의 목적지
				auto new_distance = current_vertex.distance + e.weight;
				if (new_distance < distance[neighbor]) {
					heap.emplace(Label<T>{neighbor, new_distance});
					parent[neighbor] = current_vertex.ID;
					distance[neighbor] = new_distance;
				}
			}
			visited.insert(current_vertex.ID);
		}
	}
	vector<unsigned> shortest_path;
	auto current_vertex = dst;
	while (current_vertex != src) {
		shortest_path.push_back(current_vertex);
		current_vertex = parent[current_vertex];
	}
	shortest_path.push_back(src);
	reverse(shortest_path.begin(), shortest_path.end());
	return shortest_path;
}

int main() {
	using T = unsigned;
	auto shortest_path = CDIJKSTRA<T>(G, 1, 6); //여기서 G는 위 코드의 create_reference_graph<T>를 가져오는 것이다
	cout << endl << "The shortest path between the vertex 1 and 6" << endl;
	for (auto v : shortest_path)
		cout << v << ' ';
	cout << endl;

    return 0;
}

추가적으로 같이 보면 좋을 것 같은 코드를 첨부해보았다

#include <vector>
#include <iostream>
#include <queue>
 
#define MAX 100        // 최대 정점의 개수 
#define INF 99999999
 
using namespace std;
  
vector<int> dijkstra(int start, int V, vector<pair<int,int> > adj[]) {
    vector<int> dist(V, INF);    // 전부 INF로 초기화 
    priority_queue<pair<int, int> > pq;
    
    dist[start] = 0;
    pq.push(make_pair(0, start));    // 시작 정점 방문 
 
    while (!pq.empty()) {
        int cost = -pq.top().first;    // 방문한 정점의 dist 값 
        int cur = pq.top().second;    // 현재 방문한 정점 
        pq.pop();
 
        for (int i = 0; i < adj[cur].size(); i++) {    // 현재 방문한 정점의 주변 정점 모두 조사 
            int next = adj[cur][i].first;    // 조사할 다음 정점 
            int nCost = cost + adj[cur][i].second;    // 현재 방문한 정점을 거쳐서 다음 정점을 갈때의 비용 
            if (nCost < dist[next] ) {     // 기존 비용보다 현재 방문한 정점을 거친 비용이 더 싸다면 
                dist[next] = nCost;    // 갱신 
                pq.push(make_pair(-nCost, next));    // pq에 저장 
            }
        }
    }
    
    return dist;
}
 
int main()
{
    int V,E;
    vector<pair<int, int> > adj[MAX];
    cout << "정점의 개수 입력 : ";
    cin >> V;
    cout << "간선의 개수 입력 : ";
    cin >> E;
 
    for (int i = 0; i < E; i++) {
        int from, to, cost;
        cout << "그래프 입력 [정점 정점 가중치]: ";
        cin >> from >> to >> cost;
        adj[from].push_back(make_pair(to, cost));    // 양방향 그래프 
        adj[to].push_back(make_pair(from, cost));
    }
 
    printf("\n===다익스트라 결과===\n");
    vector<int> dist = dijkstra(0, V, adj);
    for (int i = 0; i < V; i++) {
        printf("0번 정점에서 %d번 정점까지 최단거리 : %d\n", i, dist[i]);
    }
    return 0;
}

도움 받은 곳: https://code-lab1.tistory.com/29